-
0 引言
-
最近 10年,尤其近 5年来由于国内生态环境政策的实施,大型矿业公司对国内外项目并购十分活跃,以实现规模化、国际化的发展目标,如紫金矿业集团在 2020 年就成功实现了 3 个大型矿山项目的并购——中国西藏巨龙铜矿、哥伦比亚大陆黄金及圭亚那金矿山。在矿业并购过程中,要考虑的评估指标很多,例如矿山资源禀赋条件、矿山企业资产负债率、现金流、生产经营方式、采选成本、矿业投资市场化程度及投融资情况等。如何实现以最低的交易成本,获取最大的矿业项目并购交易,一直是矿业界投资者所关心及研究的热点问题。因此本次研究对矿业项目并购具有十分重要的理论意义和现实操作实用性。
-
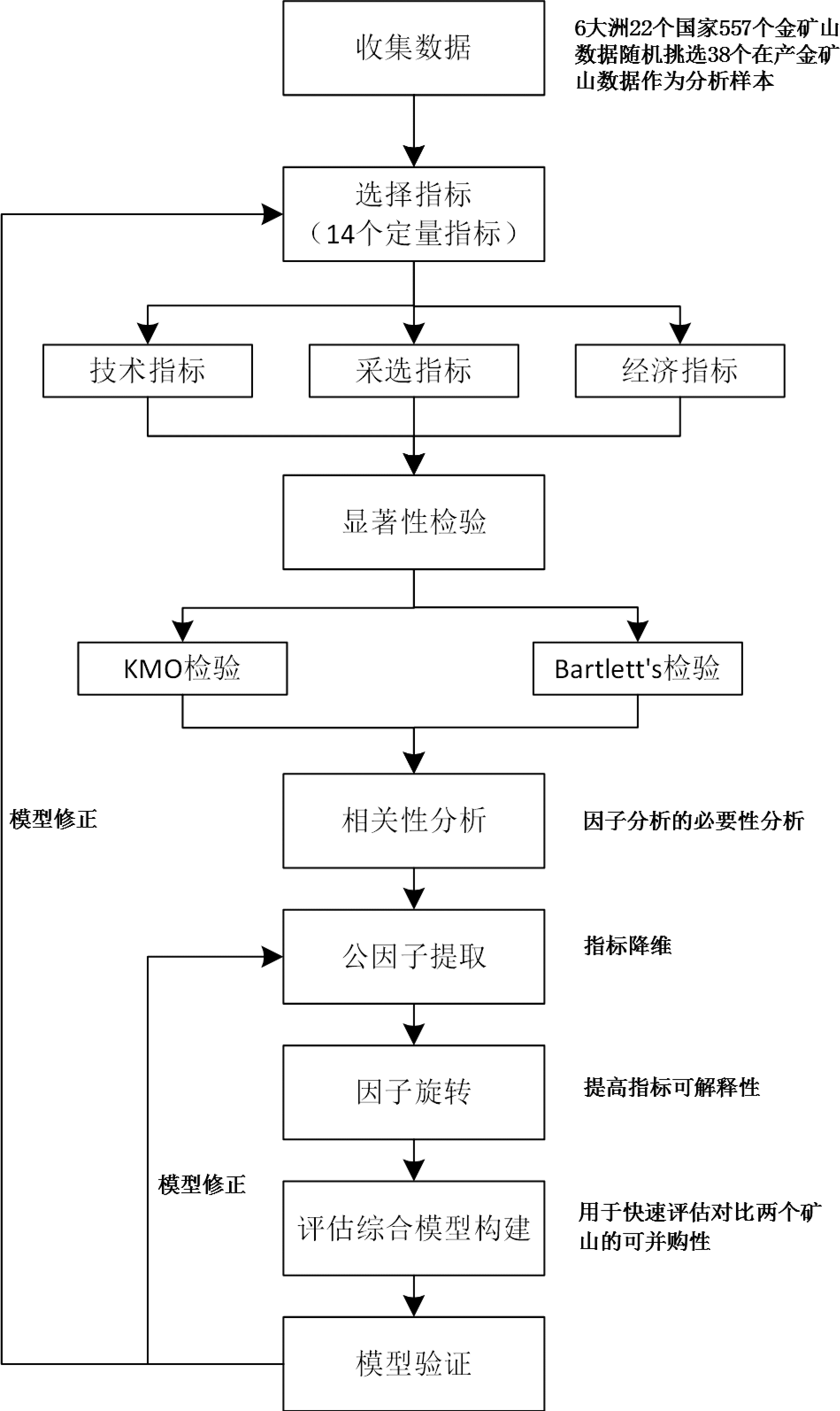
矿业项目全链条可以分为草根勘查、初勘、勘探、预可研、可研、矿山开采经营和闭坑复垦等阶段,不同勘查及开发阶段的并购有不同的关注点。本文以全球38个在产金矿山数据为研究对象,基于因子分析法对影响金矿矿业项目并购过程中的 14 个评估指标进行综合分析,并建立一套综合的评估模型,以便为同类金矿项目并购提供有价值的参考,研究流程见图1。
-
1 数据来源与研究方法
-
1.1 数据来源
-
本次研究共收集了 557 个金矿项目数据,数据来源自上市公司公开年报/储量报告、勘探报告、公司官网、标普全球财智、政府及官网、新闻、公开发表的论文及美国地调局发布的公告等。
-
图1 基于因子分析法构建评估模型流程图
-
1.2 选取样本的原则
-
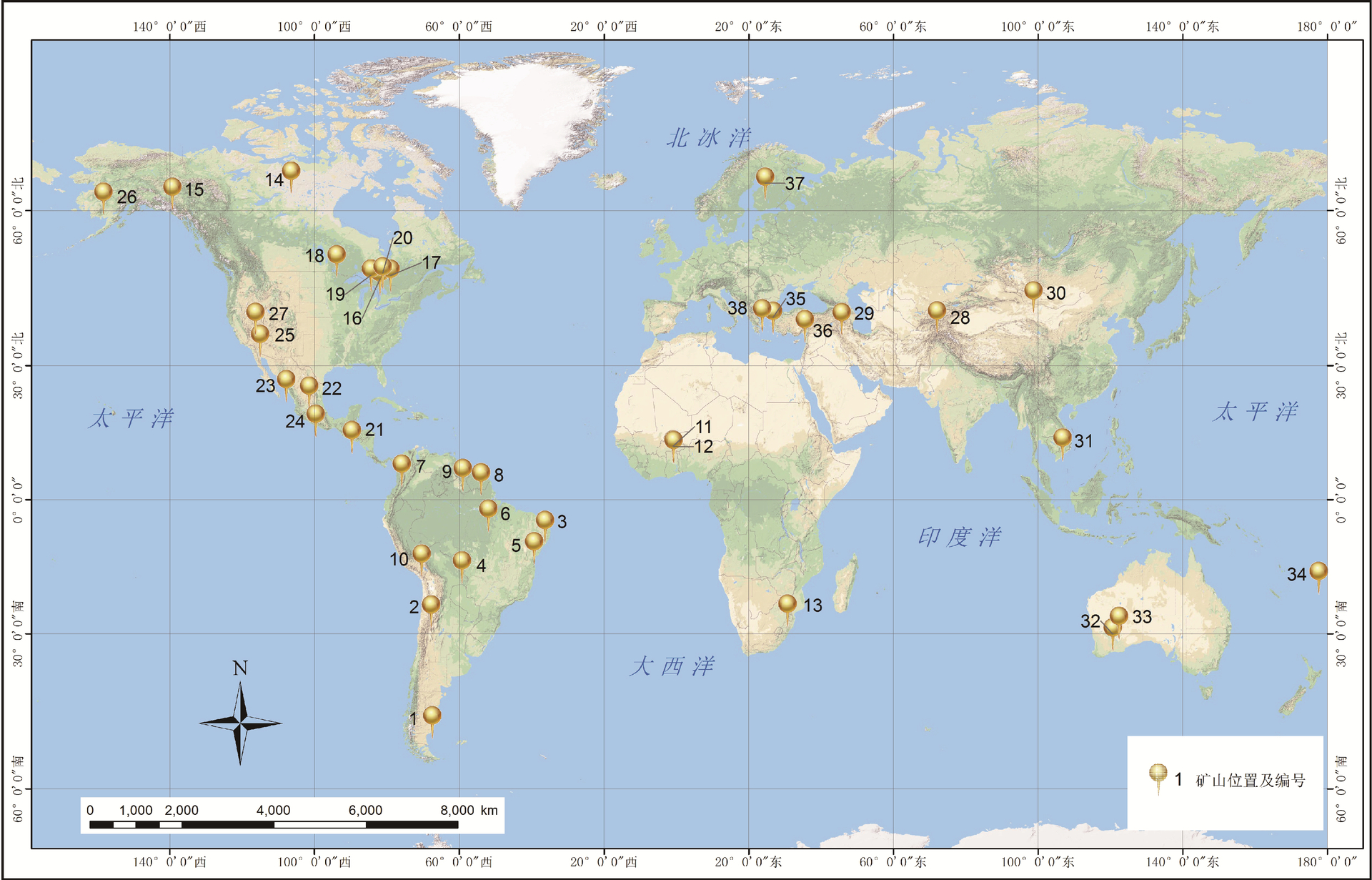
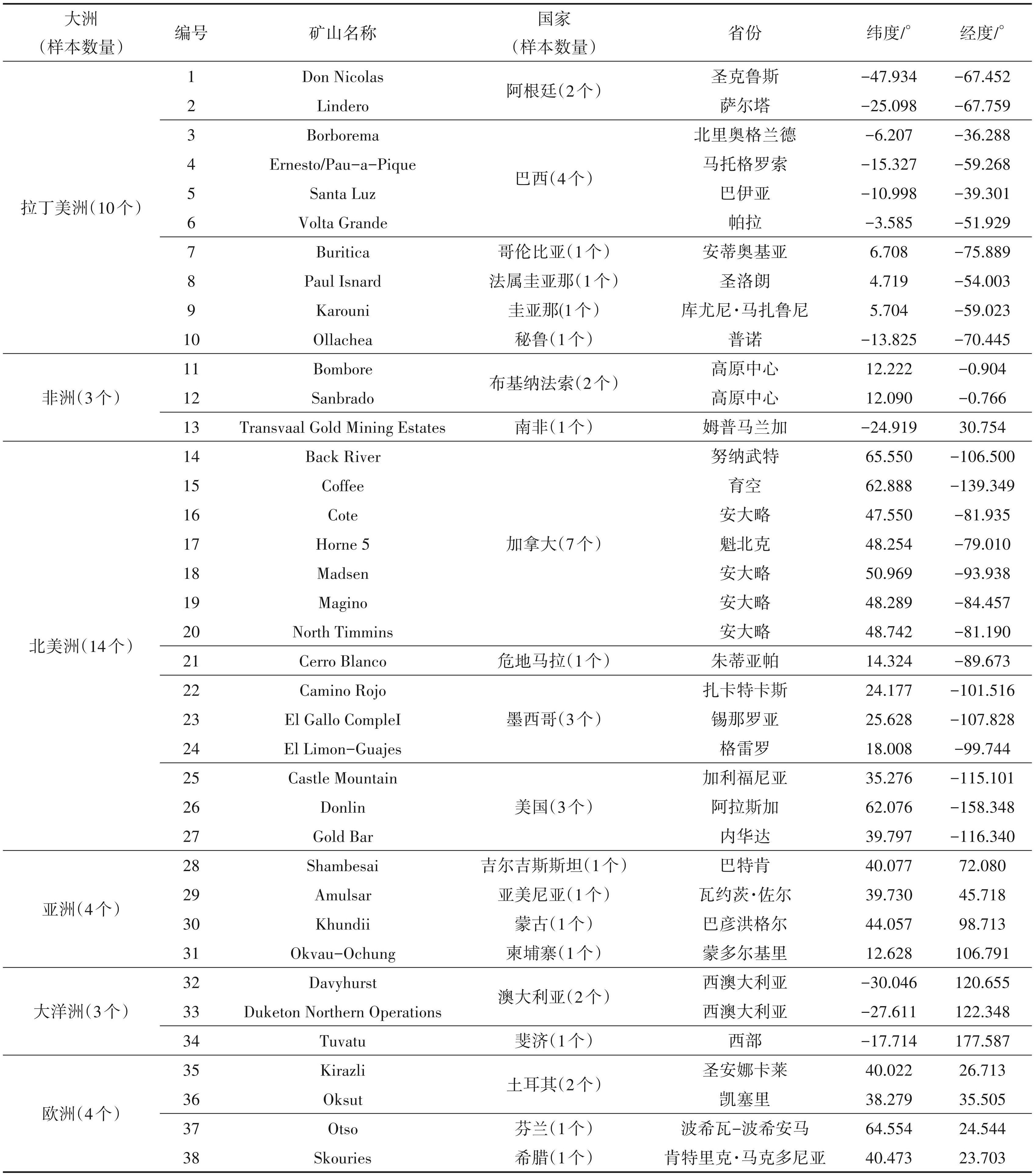
考虑到不同矿山开发阶段、不同矿种对分析过程的影响,故本文以上述557个样本作为筛选区间,基于同矿种、同时期、随机性对样本进行筛选,研究对象确定为正在开发的金矿矿山企业,数据均为 2019年的公开发布数据,据此随机筛选出38个开采阶段的金矿山作为本次研究的样本,样本数据分布于全球6大洲共计22个国家(图2,表1)。
-
图2 全球金矿山样本分布图
-
矿山编号及对应的矿山名称如下,1—Don Nicolas1;2—Lindero;3—Borborema;4—Ernesto/Pau-a-Pique;5—Santa Luz;6—Volta Grande; 7—Buritica;8—Paul Isnard;9—Karouni;10—Ollachea;11—Bombore;12—Sanbrado;13—Transvaal Gold Mining Estates;14—Back River; 15—Coffee;16—Cote;17—Horne5;18—Madsen;19—Magino;20—North Timmins;21—Cerro Blanco;22—Camino Rojo;23—El Gallo CompleI; 24—El Limon-Guajes;25—Castle Mountain;26—Donlin;27—Gold Bar;28—Shambesai;29—Amulsar;30—Khundii;31—Okvau-Ochung; 32—Davyhurst;33—Duketon Northern Operations;34—Tuvatu;35—Kirazli;36—Oksut;37—Otso;38—Skouries
-
1.3 14个分析指标的选取
-
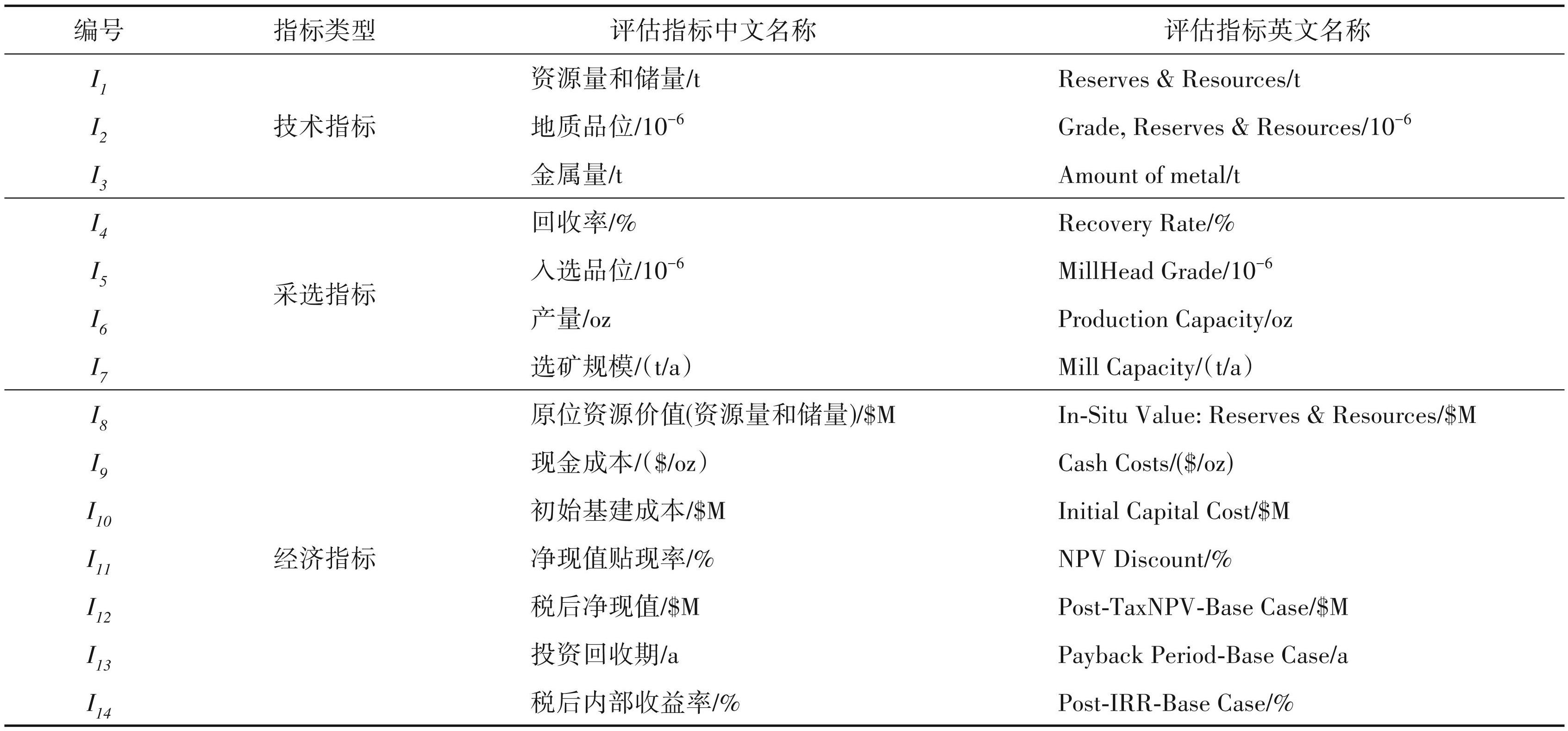
影响矿业并购的因素很多,分为定性和定量两类。如政策、基础设施、人文(社区、文化)、环保等因素属于定性指标,定性指标由专家判别,不在本文的研究范围,定量指标用于分析。笔者选取了影响矿业并购的技术指标、采选指标、经济指标3类指标类型共计 14 个定量指标进行本次的分析研究工作,评估指标及编号见表2。
-
技术指标:资源量和储量、地质品位、金属量,编号I1-I3;
-
采选指标:回收率、入选品位、产量、选矿规模,编号I4-I7;
-
经济指标:原位资源价值(资源量和储量)、现金成本、初始基建成本、净现值贴现率、税后净现值、投资回收期、内部收益率,编号I8-I14。
-
1.4 研究方法
-
本次研究工作基于统计学中的因子分析法(雷曦,2013;赵世龙等,2013;杨树琪和刘勤勤,2014; 赵国彦等,2016;刘晓萌等,2017;徐文瑞,2017;石艳敏和樊家君,2019;牛建英等,2020;周明等,2020)。因子分析法是一种降低维度的方法(丁绍芳,1991;王丽燕和张金利,1997;黄晓莉,2008;王雄军等,2008;刘玲芳和唐棠,2011;赵岩和郭嘉, 2012;范坤和冯长焕,2013),其基本原理是在众多的不同类别且相关性较低的变量组之间找出联系比较紧密的变量,并将它们归为一类,从而发现评估指标之间内蕴的关系,以便为并购实践提供理论依据。
-
因子分析是一个客观计算同主观思维相结合的过程,用因子分析的计算结果可以看作是一个中间结果,剩下的部分要求矿业投资者用专家知识进行分析和解释,涉及矿业并购的知识和经验,补足对定性指标认识的同时,符合矿业并购项目的复杂性。
-
2 评估指标分析及模型构建
-
2.1 评估指标相关性及重要性分析
-
在进行指标重要性分析之前,运用 KMO 和 Bartlett's检验 14个样本指标的相关性,判断所选取的数据是否适用因子分析。通过检验得出 KMO 值为 0.659,Bartlett's 球形度检验近似卡方统计值为 924.555,自由度91,显著性0. 000,说明各变量之间显著相关,因此本次研究所使用的矿山样本数据的特征符合因子分析的要求。
-
本次因子分析基于SPSS 19. 0进行。从14个指标相关系数矩阵分析表明(表3),少数指标之间的相关性较弱,多数指标之间的相关性较强,证明了此次进行因子分析的必要性。
-
其中指标之间相关性大于 0.6 的共有 28 个。由大到小依次为金属量和原位资源价值为 1,初始基建成本和税后净现值为 0.980,产量和税后净现值为 0.960,产量和初始基建成本为 0.942,金属量和初始基建成本为 0.940,原位资源价值和初始基建成本为 0.940,金属量和税后净现值为 0.936,原位资源价值和税后净现值为 0.936,金属量和产量为 0.906,产量和原位资源价值为 0.906,地质品位和入选品位为 0.883,资源量和储量和选矿规模为 0.869,产量和选矿规模为 0.767,金属量和选矿规模为 0.759,选矿规模和原位资源价值为 0.757,资源量和储量及金属量为 0.746,资源量和储量及原位资源价值为 0.744,选矿规模和初始基建成本为 0.743,选矿规模和税后净现值为 0.717,选矿规模和投资回收期为 0.662,产量和投资回收期为 0.645,资源量和储量和投资回收期为 0.638,税后净现值和投资回收期为 0.631,资源量和储量和初始基建成本为 0.627,资源量和储量和税后净现值为 0.607,金属量和投资回收期为 0.604,原位资源价值和投资回收期为 0.604,初始基建成本和投资回收期为0.603。
-
说明产量和金属量,原位资源价值和金属量、产量,初始基建成本与金属量、产量、原位资源价值,税后净现值与金属量、产量、原位资源价值、初始基建成本高正相关。金属量与资源量和储量,入选品位与地质品位,选矿规模与资源量和储量、金属量、产量,原位资源价值与资源量和储量、选矿规模,初始基建成本与资源量和储量、选矿规模,税后净现值与选矿规模较高正相关。
-
其中指标之间相关性小于-0.6的共有6个。产量和净现值贴现率为-0.613,初始基建成本和净现值贴现率为-0.613,净现值贴现率和税后净现值为-0.621,金属量和净现值贴现率为-0.659,原位资源价值和净现值贴现率为-0.660,投资回收期和税后内部收益率为-0.665,说明净现值贴现率与金属量、产量、选矿规模、原位资源价值、初始基建成本中等负相关。
-
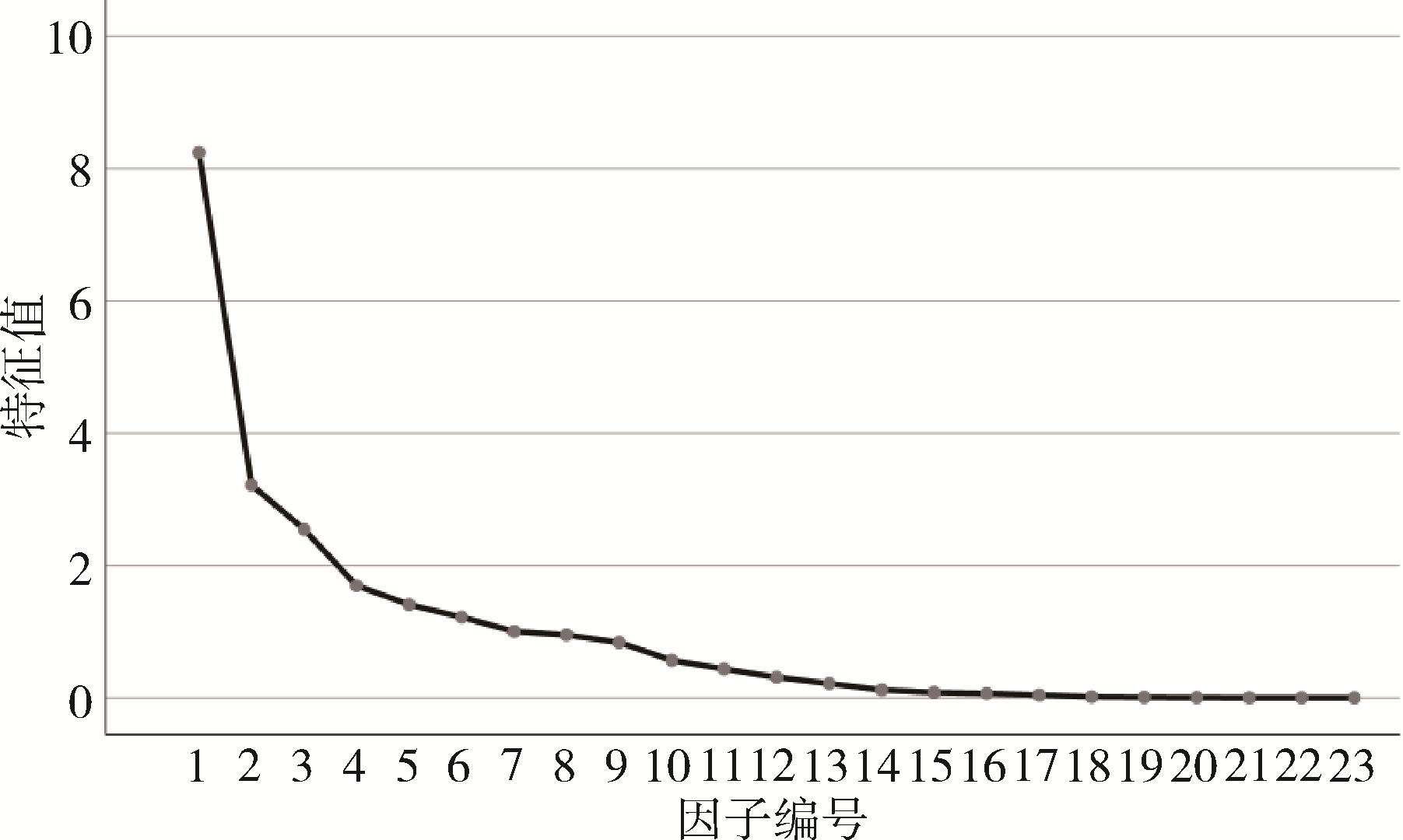
因子分析的核心是利用相关系数矩阵(表3)求出相应的因子特征值和累计贡献率。按照指标间的相关关系从多个指标里提取公因子(刘宇等, 2011)。每一个公因子,从不同方面反映矿山项目的整体情况。根据初始特征值做出碎石图(图3),并按降序将特征值排列。通过观察碎石图可知,从第 5 个公因子开始,特征值变化平缓并逐渐趋于水平(赵冬梅和闫东玲,2015)。将因子按照特征值由大到小依次排列,特征值大于 1的因子共有 4个(表4),第一个因子的特征值为 7.279,方差贡献率为 51.992%,说明当所有因子有 14 个,缩为第一个因子时,只有 51.992% 的信息被解释,其余丢失。随着因子数量的增加到第四个因子时,其累计方差贡献率达到 86.277%,表明公因子提取的结果理想,满足因子分析原则。而且旋转前后总的累计贡献率没有发生变化,即总的信息量没有损失。故提取特征值大于 1 的 4 个因子作为公因子,编号 F1、F2、 F3、F4。
-
通过以上数据认为公因子 F1和公因子 F2为影响矿业并购评估的最重要因素集,对矿山评估的贡献最大,公因子F3、公因子F4起到了较重要的作用。与公因子 F1联系紧密的指标有 I1、I3、I6、I7、I8、I10、I11 和 I12,分别为技术指标:资源量和储量和金属量;采选指标:选矿规模和产量;经济指标:原位资源价值 (资源量和储量)、初始基建成本和税后净现值。与公因子 F2联系紧密的指标有 I2、I4和 I5,分别为技术指标地质品位、采选指标回收率和入选品位。与公因子F3联系紧密的指标有I13和I14,分别为经济指标投资回收期和内部收益率。与公因子 F4联系紧密的指标为经济指标I9现金成本。
-
2.2 构建评估模型
-
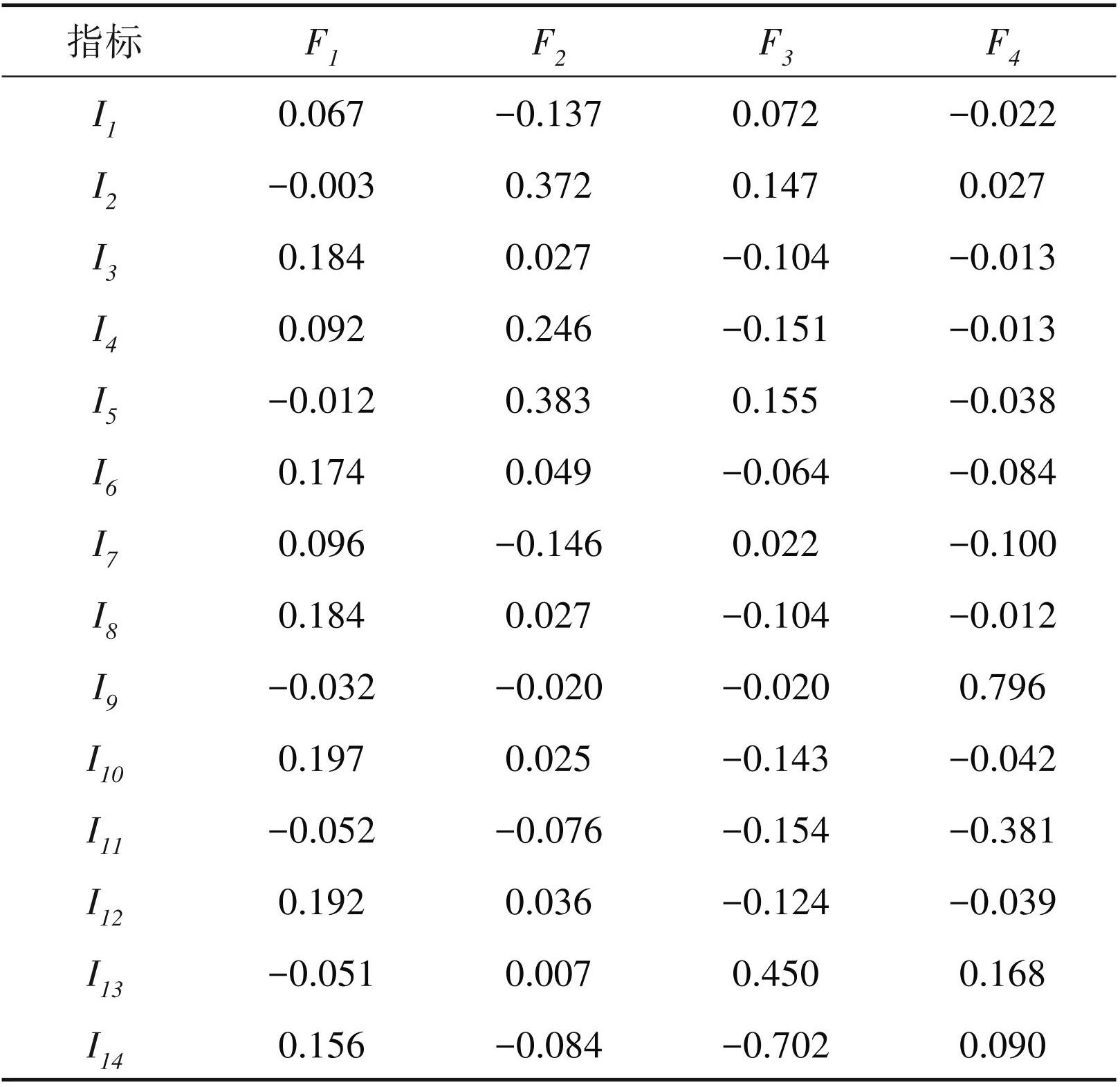
根据旋转后因子矩阵得到因子得分系数矩阵 (表5),以此写出各公因子 F 对原始指标因子的线性得分函数,由原始指标因子得分系数和标准化值计算出各公因子的权重Q(式1~4)。
-
注:提取方法为主成分分析法。
-
图3 碎石图
-
注:折线变化越陡倾斜代表对应的指标对整体事件的影响越大,越平缓对应的指标对整体事件的影响越小。
-
分别以每个公因子的方差贡献率占4个公因子总方差贡献率的比值作为系数 W(式 5~8),构建矿山并购评估的综合模型M(式9)。
-
最终得到矿山并购评估模型为:
-
通过此模型,能快速评估对比已知两个矿山的可并购性,为矿业并购提供指导和参考。如 A、B两座矿山是同一地区、同一成矿带上的两座金矿山,A 矿山为并购方在产运行良好矿山,B 矿山为拟并购矿山,将 A 和 B 两个矿山指标数据代入公式(1~4、 10),将结果MA和MB进行对比,如果B矿山计算结果大于或接近A矿山,则推荐并购。
-
紫金矿业于 2019 年 12 月 9 日和 2020 年 6 月 15 日在南美洲哥伦比亚和圭亚那完成了两个矿山的 100% 股权收购。分别为 70 亿元并购大陆黄金 100% 股权,核心资产为哥伦比亚武里蒂卡 (Buritica)金矿;以3.23亿加元通过紫金矿业金山香港全资子公司收购圭亚那金田公司 100% 股权,主要资产为奥罗拉(Aurora)金矿。
-
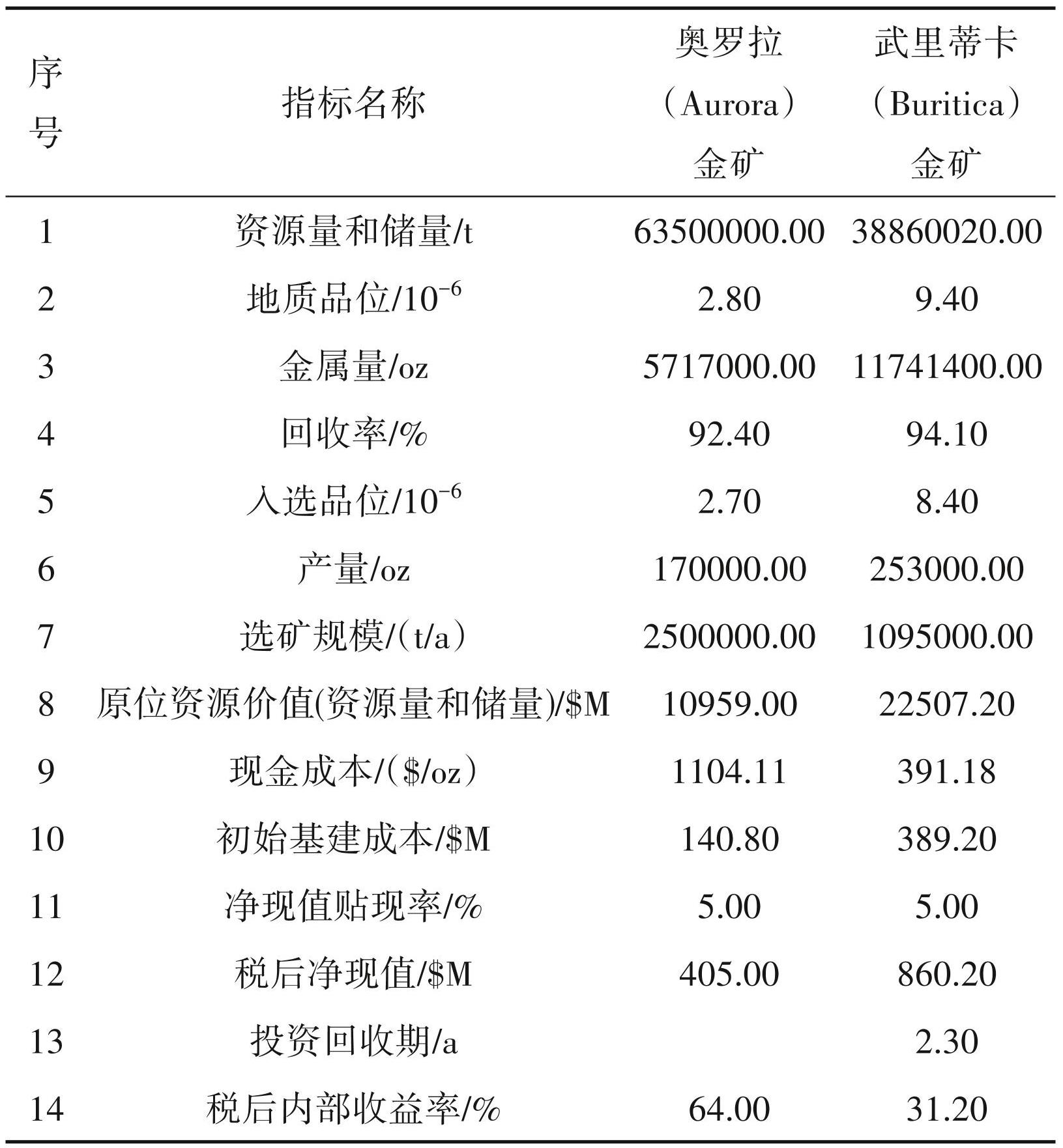
运用本次构建的评估模型公式(10)对武里蒂卡(Buritica)金矿和奥罗拉(Aurora)金矿的指标数据 (表6)进行运算,其中奥罗拉(Aurora)金矿的投资回收期数据为空,为了消除此项指标对于评估的影响,本次运算视为两个矿山的投资回收期相同,最终运算获得奥罗拉(Aurora)金矿的评估值 M 为 1760417,武里蒂卡(Buritica)金矿的评估 M 值为 1950154,两座矿山的评估值 M 相近,因此本次构建的评估综合模型对于矿山并购评估具有明显的参考意义。
-
注:数据引自标普全球财智,其中奥罗拉(Aurora)金矿资源量和储量、地质品位、金属量数据时间自2019年12月31日,武里蒂卡金矿(Buritica)资源量和储量、地质品位、金属量数据时间自2019年1 月30日。
-
3 讨论
-
通过矿山样本的分析数据和公因子的构成可以得出以下讨论观点:
-
(1)公因子 F1为 I8原位资源价值(资源量和储量)、I3金属量、I10初始基建成本、I12税后净现值、I6产量、I7选矿规模、I1资源量和储量和I11净现值比率。
-
公因子 F1对整个指标体系的方差贡献率一半左右,由此可以得出一个结论:公因子F1中的7个指标对于矿山并购指标评估时要引起足够的重视;且原位资源价值(资源量和储量)、金属量、初始基建成本、税后净现值、产量对项目并购的指标贡献率最大,选矿规模、资源量/储量、净现值比率次之。分析其原因:选矿规模虽然是资源赋存条件、开采技术条件、技术装备水平、管理水平、职工素质等综合因素,但是其缺陷性明显,当一个矿山停产的时候选矿规模指标不会改变,不能健康反映矿山的运营状态;资源量/储量是矿山资源情况的反映指标,但是本次讨论的矿种为金矿,品位对资源情况的影响很大,因此金属量指标的重要程度会高出资源量/储量;净现值比率代表了净现值和投资额的关系,其关系较为复杂,不是单纯的净现值和投资额越高越好。
-
(2)公因子 F2为 I5入选品位、I2地质品位和 I4回收率,其中入选品位、地质品位对公因子 F2的影响较高,I2回收率的影响次之。分析其原因:入选品位是入选选矿厂的矿石有用组分的平均含量,是矿山资源质量、配矿、选矿能力的综合体现指标;品位是矿山整体资源质量的反映;而回收率是选矿产品 (一般指精矿)中所含被回收有用成分的质量占入选矿石中该有用成分质量的百分比,是选矿中的一项重要技术经济指标,但是其高低对于整个矿山投资评估来说就显得重要性不足。
-
(3)公因子 F3为 I13内部收益率和 I12投资回收期。内部收益率,是一项投资渴望达到的报酬率,是能使投资项目净现值等于零时的折现率,该指标越大越好。一般情况下,内部收益率大于等于基准收益率时,该项目是可行的。投资回收期是矿山投产后获得的收益总额达到投资总额所需要的时间,其与产量、选矿规模息息相关,所以影响系数次之。
-
(4)公因子 F4为 I9现金成本。现金成本是矿山在生产经营过程中以货币形态存在的资产,是矿山企业流动资产的重要组成。
-
4 结论与建议
-
(1)本文运用因子分析法对资源量和储量、地质品位、金属量、回收率、入选品位、产量、选矿规模、原位资源价值(资源量和储量)、现金成本、初始基建成本、净现值贴现率、税后净现值、投资回收期和内部收益率 14 个矿山并购评估指标分析研究表明,矿山项目并购的 14个因素指标可以归为 4个公因子,指标之间的相关性和重要性不同,具体为:公因子F1:原位资源价值(资源量/储量)、金属量、初始基建成本、税后净现值、产量,其是矿山并购评估的最重要影响指标;公因子 F2:选矿规模、资源量/储量、净现值贴现率,贡献率次之;公因子 F3:入选品位、地质品位、回收率、内部收益率、投资回收期;公因子 F4:现金成本其重要性依次降低。构建了矿山并购指标评估的综合模型,并运用武里蒂卡 (Buritica)金矿和奥罗拉(Aurora)金矿进行了运算分析,结果表明模型具有明显的借鉴意义,可为今后金矿矿山并购提供参考。
-
(2)本次研究的不足是以在产金矿的数据作为原始样本,由此得到的模型只能适用于对该矿种的研究和预测。对于评估铜、铅锌等有色金属、稀有金属和黑色金属矿山项目不完全适用,要根据并购矿业项目的具体特点进行完善,这样才能得出比较符合实际的评估效果。基于矿业并购的复杂性,笔者下一步会针对不同矿种、不同区域的矿山进行更深入的研究,以期运用矿业并购大数据的智能分析模拟预测出矿山投资价值,为矿业并购提供服务。
-
致谢 此次研究工作是对矿山并购指标模型化的一次尝试,为未来矿山智能评估和快速评估奠定了基础。在撰写过程中与和志军教授级高级工程师进行了深入的交流,感谢其提出的宝贵建议。由于笔者水平有限,存在着诸多的不足,不妥之处,敬请专家批评指正。
-
参考文献
-
丁绍芳. 1991. 全国中型钨矿山企业经济效益指标的因子分析[J]. 北方工业大学学报, (1): 31–40.
-
范坤, 冯长焕 . 2013. 因子分析中指标数据如何正确预处理[J]. 财会月刊, (6): 85–88.
-
黄晓莉. 2008. 因子分析法在行业经济效益综合评价中的应用[J]. 经济论坛, (3): 59–62.
-
雷曦. 2013. 我国矿业上市公司财务质量综合评价研究[D]. 北京: 中国地质大学(北京).
-
刘玲芳, 唐棠 . 2011. 基于因子分析法的钢铁业上市公司财务评价 [J]. 财会通讯, (27): 122–124.
-
刘晓萌, 孟祥瑞, 何叶荣, 汪克亮 . 2017. 基于因子分析的矿业城市转型能力统计分析与测评[J]. 湖南科技大学学报(社会科学版), 20(3): 109–114.
-
刘宇, 赵怡晴, 李仲学, 李翠平 . 2011. 基于因子分析法的矿业企业 SR水平综合评价[J]. 矿业研究与开发, 31(6): 99–103.
-
牛建英, 胡小明, 吴文静. 2020. 资源枯竭型城市经济转型效果评价 ——以黄石市为例[J]. 中国名城, (4): 9–15.
-
石艳敏, 樊家君 . 2019. 基于因子分析的我国矿产行业上市公司盈利能力评价[J]. 企业科技与发展, (12): 161–163.
-
王丽燕, 张金利 . 1997. 因子分析法在矿山企业评价中的应用[J]. 鞍山钢铁学院学报, (5): 14–17.
-
王雄军, 赖健清, 鲁艳红, 李德胜, 周继华, 王建武 . 2008. 基于因子分析法研究太原市土壤重金属污染的主要来源[J]. 生态环境, (2): 671–676.
-
徐文瑞 . 2017. 基于因子分析法的矿业企业 SR 水平综合评价[J]. 中国锰业, 35(4): 163–165.
-
杨树琪, 刘勤勤 . 2014. 我国矿产资源税收制度改革的影响因子分析[J]. 云南财经大学学报, 30(5): 153–160.
-
赵冬梅, 闫东玲 . 2015. 基于因子分析和聚类分析的中小制造企业信用评级研究[J]. 电子设计工程, 23(7): 82–85.
-
赵国彦, 赵爽, 孙杨, 秦亚光 . 2016. 因子分析法在尾矿库环境评价中的应用[J]. 环境工程, 34(S1): 874–877.
-
赵世龙, 王文顺, 赵尔铎, 顾曼 . 2013. 建设项目决策风险因素分析 ——基于因子分析法[J]. 建筑经济, (8): 39–42.
-
赵岩, 郭嘉 . 2012. 指数因素分析法在矿山企业成本分析中的应用 [J]. 现代商贸工业, 24(15): 127–128.
-
周明, 庄晶, 肖谷. 2020. 基于因子分析法的环境信息披露质量评价 ——以采矿业上市公司为例[J]. 东华理工大学学报(社会科学版), 39(2): 126–131.
-
摘要
本文收集和整理了 6大洲 22个国家的 38个在产金矿山样本数据的 14个指标,采用因子分析法对开发阶段金矿项目并购中的14个参数指标进行显著性检验、指标分析、公因子提取及因子旋转。结果表明影响开发阶段金矿项目并购的 14 个指标可归为 4 个公共因子,4 个因子的重要性依次降低。其中公共因子 1:原位资源价值(资源量和储量)、金属量、初始基建成本、税后净现值、产量,是最重要影响因子;公共因子2:选矿规模、资源量和储量、净现值贴现率;公共因子3:入选品位、地质品位、回收率、内部收益率、投资回收期;公共因子4:现金成本。同时构建了开发阶段金矿项目并购指标综合评估模型,并运用武里蒂卡 (Buritica)金矿和奥罗拉(Aurora)金矿进行了运算分析,结果具有明显的借鉴意义,以期为国内外金矿项目并购提供参考。
Abstract
This paper collects and organizes 14 indicators of sample data from 38 gold mines in 22 countries on six continents, using factor analysis method to conduct significance testing, indicator analysis, common factor extraction, and factor rotation on 14 parameter indicators in the development stage of gold mine project mergers and acquisitions. The results indicate that the 14 indicators that affect the mergers and acquisitions of gold mining projects in the development stage can be classified into 4 common factors, and the importance of these 4 factors decreases in sequence. Among them, common factor 1 is the In-Situ Value: reserves & resources, amount of metal, initial capital cost, post tax NPV, production capacity, which are the most important influencing factors; Common factor 2 is mill capacity, reserves & resources, NPV discount; The public factor 3 is mill head grade, geological grade, recovery rate, internal rate of return and payback period; Common factor 4 is the cash costs. Constructed a comprehensive evaluation model for the merger and acquisition indicators of gold mining projects in the development stage, and the calculation and analysis are carried out by using Buritica gold mine and Aurora gold mine. The results have obvious reference significance, to provide reference for mergers and acquisitions of domestic and foreign gold mining projects.