0 引言

矿产勘查的目的是提交可供矿山设计和开发利用的资源量（Ortiz and Emery，2006；马艳平等， 2019；白丽伟，2021；邹进超等，2021；李金勇等， 2022）。与勘查阶段的资源量估算工作不同，矿山设计和开发阶段的资源量估算，主要服务于矿山日常生产组织（如年、季、月生产计划；采场品位控制、两率管理；金属平衡管理等）和中长期发展规划。尽管勘查阶段符合规范要求的勘查工程间距看似合理，但往往难以准确刻画矿体的三维连续性，而引起资源量估算的偏差（高帮飞，2016）。资源量可靠程度达到 80% 完全满足勘查阶段对探明资源量的要求（国家质量监督检验检疫总局和国家标准化管理委员会，2020），但对于采选冶矿山而言，20% 的矿石量或者品位偏差，会对矿山生产组织带来巨大影响。矿石量的减少会缩短矿山服务年限；而品位的偏差既影响矿山经济效益，又影响企业中长期的生产规划，以及矿山产量、处理量、选冶指标稳定性等具体问题。这种情况下，大多数矿山选择在设计与开发过程中进行补充勘探和生产勘探，目的就是对矿化体三维形态进一步约束，提供更多的样品点数据，用于更精确的三维建模与资源量估算。因此，矿山资源量估算的本质要求是控制资源量风险，把资源量估算尤其是品位的估值偏差降到最低，为矿山开发和规划提供准确的基础数据。

尽管影响资源量估算可靠程度的因素较多，如勘查工程间距，工程施工、取样、化验质量，特异值处理，矿（化）体形态圈定，块划分，搜索椭球形态方位和大小，变异函数，幂次等。然而归纳起来，资源量估算最核心的问题是确定参与资源量估算的样品点数据，以及其相应的权重。理论上，参与估值的品位数据应具有地质和统计上的相关性和一致性（Guibal，2001；Duke and Hanna，2001；Sinclair and Blackwell，2002）。传统几何法估算资源量多侧重于矿床的经济性，其矿体圈定采用一般工业指标或经设计院论证过的工业边界品位，且矿体内的数据均参与资源量估算。当矿体与围岩界线截然时，这种方法是适用的；而当矿体与围岩呈渐变关系时，圈定矿化域的优点更突出（中华人民共和国自然资源部，2020）。但是，规范并没有给出具体的判定方法。

距离幂次反比（Inversed Distance Weighting， IDW）方法因操作简单、对样品数据分布和空间构型没有特殊要求等优点，被广泛应用于资源量估算 （李章林等，2008；沈阳等，2012）。根据国内最新的勘查规范，采用距离幂次反比法估算资源量时，可按传统（几何法）资源量估算方法圈定矿体，建立地质模型，估算出矿体的资源量；也可以合理确定矿化边界品位，先圈出矿化域，建立地质模型，再通过估值计算出工业品位矿块、低品位矿块和废石块，圈出矿体（国家质量监督检验检疫总局和国家标准化管理委员会，2020）。矿化域边界品位的确定目前尚没有公认的成熟方法。一般可从样品分布直方图、累计分布曲线、概率图中寻找矿化拐点确定，或通过类比法确定，或采用边界品位的 1/2确定，或根据尾矿品位值确定（中华人民共和国自然资源部，2020）。

当前，国内正处于矿床工业指标体系与矿块指标体系共同运行的时期，尤其是矿块指标体系方法流程写进国家和行业规范的时间还不长，估值指标体系方法的选择及相关参数的确定还处于不断摸索和实践阶段。近年来，笔者依托自然资源部境外专项并配套多个重点科研课题，研发一套改进的IDW 估值新方法，通过引入分形分析、边界分析和变异函数分析等技术，来圈定资源量估算的矿化域、确定最终的估算域以及定量化估值关键参数，大幅提高了资源量估算准确度和可重现性（高帮飞等，2012，2017，2018，2021；高帮飞，2018；李红兵和高帮飞，2021；陈伟康等，2022；谢徽，2023；谢徽等， 2023a，2023b）。该方法技术获得多项国家发明专利 （高帮飞等，2017，2018），在国内外多个矿山项目进行了实际化应用，并取得良好的技术经济效益。本文以矿块指标体系的估值流程为技术路线，在系统介绍改进IDW方法的关键技术基础上，以刚果（金） 绿纱铜钴矿床的资源量估算为例进行应用，并通过探采对比验证方法的可靠性，以期与同行交流。

1 现行资源量估算存在的主要问题

1.1 品位估值基本原理

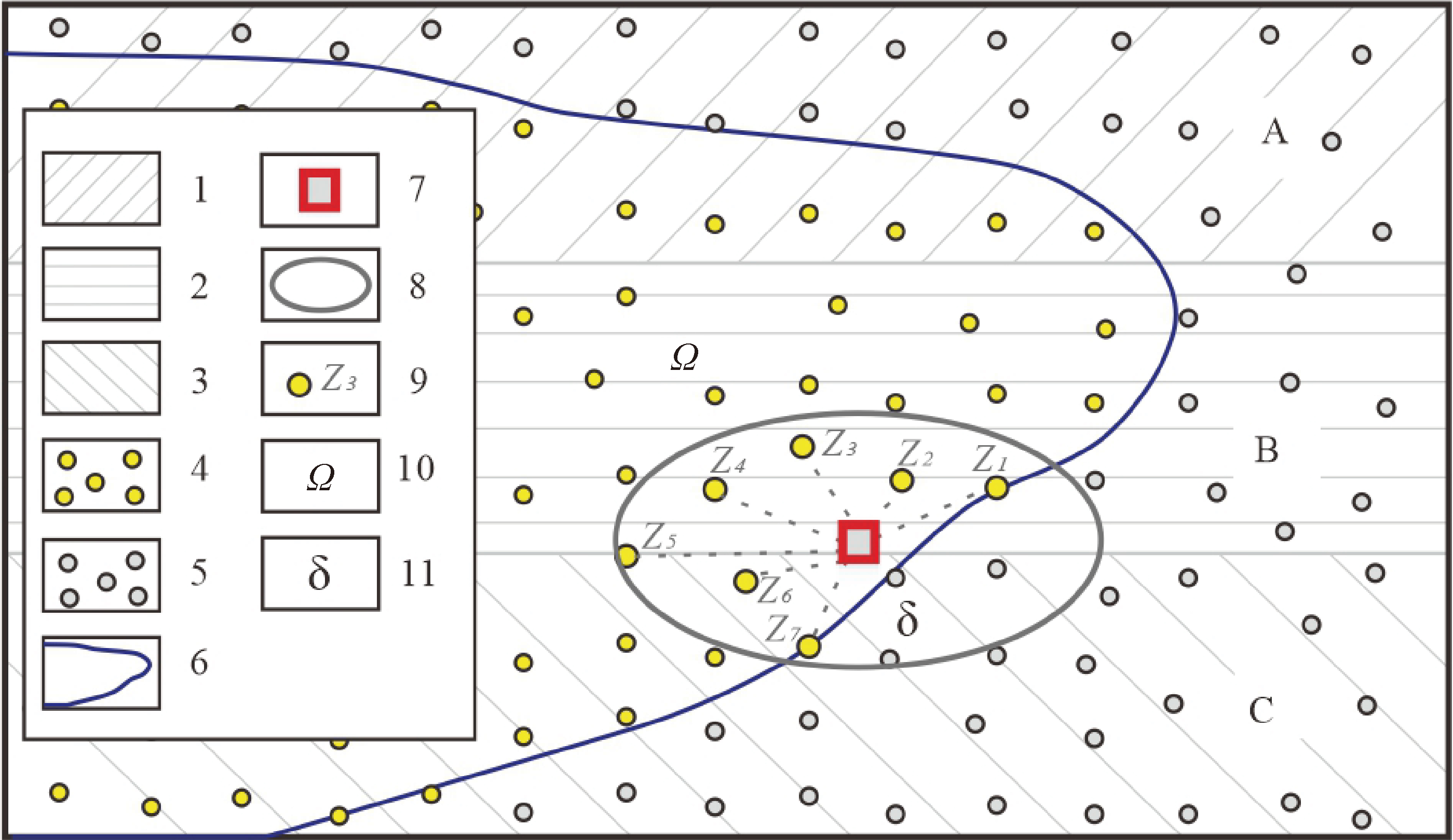
资源量估算的关键是对未知块的品位估值。品位估值不是基于所有的勘查数据，而是采用未知块附近一定邻域内的样品点数据。不论是传统几何法（如平行剖面法）还是IDW法和克里格法，都是这种局部估值工具（图1），其基本公式如下：

式（1）中：Ω为估算域范围；δ为估值邻域；Z（x）^* 为未知块的估计值；z（x_i）为估值邻域δ内第i个样品品位值；w（x_i）为对应样品点权重。

对参与估值样品点数据的约束，取决于矿体或矿化体的圈定以及最终估算域的确定。由于样品点数据兼具地质属性和技术经济属性，一般是根据矿化的分布规律，先圈定控制矿化的地质界线（即 geological domain 或地质域，例如图1 中的 A、B、C，主要的矿化均分布于这3种地层或岩性之中），再根据技术经济的要求，设置不同的边界品位圈定出矿体或矿化体（也即 grade shell or grade domain/品位域，用矿化的边界品位圈定出的矿化体，也称作矿化域）。多数情况下，圈定的品位域，也就是最终的估值域（图1中Ω）。

1—地层或岩性A；2—地层或岩性B；3—地层或岩性C；4—估算域边界内样品点；5—估算域边界外样品点；6—估算域边界；7—待估值块； 8—搜索椭球；9—参与估值样品点；10—估算域；11—估值邻域

估值域和参与估值的样品点数据确认后，因估值方法的不同，其估值邻域和样品点权重等关键参数的确定也存在差异。平行剖面法的估值邻域是基于勘查工程围限形成的块段，并采用块段相关工程样品长度作为权重；IDW 和克里格法则的估值邻域是基于搜索椭球，IDW 法样品点权重为距离幂次的倒数，而克里格法权重确定是基于变异函数分析基础上进行最优、无偏估计得到。

1.2 传统IDW资源量估算的主要步骤

IDW 方法受原始样品数据的稀疏程度、数据空间构型和统计特征影响较小，方法流程较为简单，相比克里格方法，更适合在生产一线推广使用。基于上述品位估值原理，结合勘查规范要求，传统IDW 资源量估算的关键步骤为：①根据工业边界品位或矿化边界品位，圈定矿体或矿化体；②利用上述矿体或矿化体三维展布形态和勘查工程间距，确定搜索椭球产状、轴比和半径；③采用 IDW 法对估值邻域内样品点数据赋权重，计算得到未知块估值结果；④统计特定边界品位条件下，矿体或矿化体边界内块体积、体重和估值品位信息，得到相应的估算矿石量、平均品位和金属量。

1.3 值得商榷的主要问题

传统IDW估值尽管采用了矿块指标体系（中华人民共和国自然资源部，2020），但其圈矿及估值过程中关键参数的确定与地质工程师的认识水平密切相关，工作流程缺少定量化，可能会对估值的准确性和可重现性产生影响。传统 IDW 估值流程尚待改进的地方包括：①直方图、CDF、概率图法确定矿化边界品位，有时难以识别出有效拐点，无法给出矿化域的下限（高帮飞等，2017）；②规范提出采用IDW方法时，圈矿既可以用工业边界品位来圈定矿体，也可以用矿化边界品位来圈定矿化体，但并没有给出具体的判定方法，经验表明，如果矿化在矿体与围岩之间呈渐变过渡特征而采用工业边界品位来圈定矿体，会增强矿体内高品位矿化的连续性，可能导致高品位矿石的吨位和品位的高估 （Stegman，2001；Glacken and Snowden，2001；Sinclair and Blackwell，2002；孙玉建等，2006；高帮飞，2018； 陈伟康等，2022）；③传统IDW方法不采用变异函数分析，其估值的幂次和搜索椭球半径参数的确定缺少定量化依据。

2 改进 IDW 估算方法的关键技术

笔者针对上述不足，基于矿块指标体系，提出一套改进的 IDW 估值新方法，通过引入分形分析、边界分析和变异函数分析等技术，来圈定资源量估算的矿化域、确定最终的估算域以及定量化估值关键参数，其技术流程如下。

（1）通过分形分析，去除特异值，获得资源量估算的矿化域（先圈地质域，再圈品位域），手工圈定矿化域边界，后续数据统计分析和资源量估算均在该边界内，矿化域边界外的数据不参与资源量估算。

（2）开展边界分析，对上述地质域以及矿山生产关注的工业品位域进行边界分析，判定这些矿化域是合并还是单独作为估算域；换言之，根据边界的性质（硬边界、软边界、半软边界）来判断地质域或工业品位域边界外数据是否参与资源量估算，也即确定最终的估算域。

（3）基于估算域内数据的全向变异函数分析，获得最优变程，作为未知矿块品位估值的邻域，进一步缩小参与未知块估值的样品数据范围；同时，根据井向变异函数拟合获得块金效应值，来确定距离幂次反比估值时的幂次，并最终得到参与估值已知样品点的权重。

（4）利用探采对比数据进行局部或总体验证，根据对比结果进一步修正和完善估值参数。

3 分形分析与矿化域圈定

分形的概念最早由 Mandelbrot（1982）提出。分形方法可以有效判别多期次或不同类型的矿化叠加作用（Blenkinsop，1991；Cheng et al.，1994）。近年来，分形方法被广泛应用于勘查地球化学数据的背景场与异常值的分离（Zuo，2011；Wang et al.，2013； Saein and Afzal，2017）。分形分析应用于资源量估算，主要是利用分形方法更加准确地刻画矿床的内部结构和性质，揭示样品点数据的几何特征和分布规律，从而提高资源量估算的准确性和效率 （Rahimi et al.，2018；Mohammadpour et al.，2019）。笔者采用 Number-Size（N-S）模型，进行样品品位数据的混合总体筛分。该方法的主要流程为（高帮飞等，2017）：首先将控制矿化分布的地质域内所有勘查工程品位数据进行等长组合，组合后数据按从小到大顺序排列；根据 N-S 模型，若品位数据满足分形分布则有N（r）=Cr^-D，其中r为品位值，N（r）为品位大于r的样品个数，C为常数，D为分维值，对于给定不同的品位 r，统计大于或等于 r的品位数据个数 N （r），在双对数图lgr~lgN（r）上做散点图；用最小二乘法拟合（拟合优度≥0.950），拟合直线斜率的绝对值就是分形维数D。一般地，分形维数越高，表明变量之间的相关性越强。然而，并不是所有数据点都符合分形分布特征（Blenkinsop，1991），把具有分形分布特征的品位区间称作分形标度区间，所有分形标度区间的变化范围称为分形范围（Fractal range）。在此基础上，识别出特异值（包含特高值和特低值），确定矿化品位域。由于大量矿化样品数据参与统计分析，分形方法确定的矿化域下限值一般为低于边界品位的数据，最大程度保持了样品数据空间结构的连续性。

通过与工业指标、直方图法、CDF、m+3σ 法、σ/ m、Decile Analysis 和 Cutting Curve Plots 等方法的对比，总结分形方法的优点在于（高帮飞等，2017）： ①分形方法既可以给出矿化域和特异值，又可以根据分形结构细分品位域，与多期次矿化作用特征相对应，给出品位分布的地质意义；②可以同时识别出特高值和特低值；③分形方法可操作性和重现性强，人为干扰相对较少，易于推广使用。

4 边界分析与估算域确定

边界分析的原理是通过考察特定地质或品位边界附近样品点的数值变化，来判断品位数据之间的相关性（Stegman，2001；Sinclair and Blackwell， 2002；Ortiz and Emery，2006；Emery and Robles， 2009；Wilde and Deutsch，2012；Rossi and Deutsch， 2014；Abzalov，2016；高帮飞，2018；高帮飞等，2021； 谢徽等，2023b）。如果边界内外品位存在突变，表明样品点数据空间相关性弱，该边界为硬边界，反之如果品位是渐变变化，表明样品点数据的空间相关性强，该边界为软边界或半软边界。硬边界条件下，仅采用域内数据进行估值；软边界或半软边界条件下，采用域外一定范围内样品数据进行估值。

边界分析的目的在于判断地质域或品位域是否需要合并，以确定最终的估算域。估算域划分过小会导致参与资源量估算的样品点数据太少，而影响品位统计分析和估值的可靠性（Rossi and Deutsch，2014）。此外更为重要的是，边界类型划分对品位估值结果有着直接影响。高品位域中带入大量低品位域的数据，将导致估值整体偏低；相反，原本属于软边界类型的，若采用硬边界条件进行估值，将人为增强高品位数据的连续性（Stegman， 2001；Sinclair and Blackwell，2002；Rossi and Deutsch，2014；高帮飞，2018）。

此外，边界分析可以加深对矿化连续性的理解。例如，我们对存在氧化矿和硫化矿两种矿石类型的矿床进行资源量估算时，一般做法是单独圈定氧化矿体和硫化矿体，并分开进行估值。又如，对于工业矿体内部存在连续的高品位矿段，勘查规范推荐圈定“工业富矿体”并单独进行估值。边界分析告诉我们，这些传统做法是值得进一步商榷的，需要运用地质和统计的方法对地质域或品位域的边界条件进行判断。

a—氧化矿与硫化矿地质域边界模型及Cu品位域模型；b—0.45%~1. 0% Cu品位域模型；c—1. 0%~2.7%Cu品位域模型；d—2.7%~16. 0%Cu 品位域模型

以刚果（金）某铜钴矿的地质建模为例进行说明。该矿床上部为氧化矿体，下部为硫化矿体，地质编录资料表明，二者界面标高在1280 m左右。用分形方法确定分形分布范围为 0.45%~16. 0%。分形区间的拐点为 0.45%、2.7% 和 16. 0%。其中， 0.45% 为特低值，16. 0% 为特高值。考虑到刚果 （金）地区一般工业边界品位为 1. 0%，结合分形区间拐点 0.45% 和 2.7%，将分形区间 0.45%~16. 0%分为多个品位域。即低品位域（矿化域）0.45%~1. 0%，工业品位域 1. 0%~2.7%，中高品位域 2.7%~16. 0%。利用隐式建模技术，完成了 3 个品位域和氧化矿/硫化矿地质域的三维建模（图2）。隐式建模最大的优点是省去了大量手工数字化过程，可以直接根据品位的数值化赋值结果快速生成表面。基于边界品位 0.45%、1. 0% 和 2.7%，以及氧化矿/硫化矿地质域边界的边界分析见图3。不难看出，各品位域边界内外和地质域边界上下，样品点数据的平均品位均呈渐变过渡特征，显示了较强的相关性和连续性，说明上述各类边界均为软边界条件。因此，不论是氧化矿与硫化矿，还是低、中、高品位域均应合并成新的估算域进行资源量估算。采用 0.45%~16. 0% 作为估算域范围的资源量估算结果与实际生产情况的对比表明，软边界条件下，工业品位块模型的体积、矿石量略高于生产数据，而铜平均品位稍低于生产数据，铜金属量与实际生产数据基本一致，说明估算方法的准确度较高（谢徽等， 2023b）。

a—以0.45%为矿化低品位域边界的边界分析；b—以1. 0%为工业品位域边界的边界分析；c—以2.7%为中高品位域边界的边界分析； d—氧化矿/硫化矿界面（1280 m标高）的边界分析

5 变异函数分析与估值邻域和权重的确定

传统的 IDW 估值参数确定并不采用变异函数分析的结论。估值时搜索椭球形态、方位及样品点权重，主要取决于矿化体的三维形态、展布方向及样品品位数据的变化系数，这与地质工程师的认知有很大关系。然而，研究表明IDW估值参数与变异函数之间存在着紧密的联系。Coombes（2008）提出 IDW 幂次与块金效应呈负相关关系。笔者在系统研究了块金效应、屏蔽作用、变程及幂次之间的关系后认为，IDW 估值结果三维空间分布结构（如所谓的“牛眼构造”的强弱）受距离和幂次制约，类似于块金效应或屏蔽作用反映出来的数据特征，二者有相通之处（李红兵和高帮飞，2021；高帮飞等， 2021）。研究表明，若变异函数块金效应越小，则屏蔽作用越强，IDW幂次应选择高幂次（在4~5之间），估计邻域范围适当缩小，可与变程相当；反之若块金效应大，则屏蔽作用弱，IDW 幂次可选择低幂次 （在1~2之间变化），估计邻域范围应适当扩大；当存在纯块金效应时，IDW幂次取值为0，各样品点权重相同，与距离无关，估计领域范围可以扩大到整个矿化域。具体操作过程中，块金效应值利用井向变异函数确定，而最优变程则采用全向变异函数的拟合值。

6 应用实例

6.1 地质概况

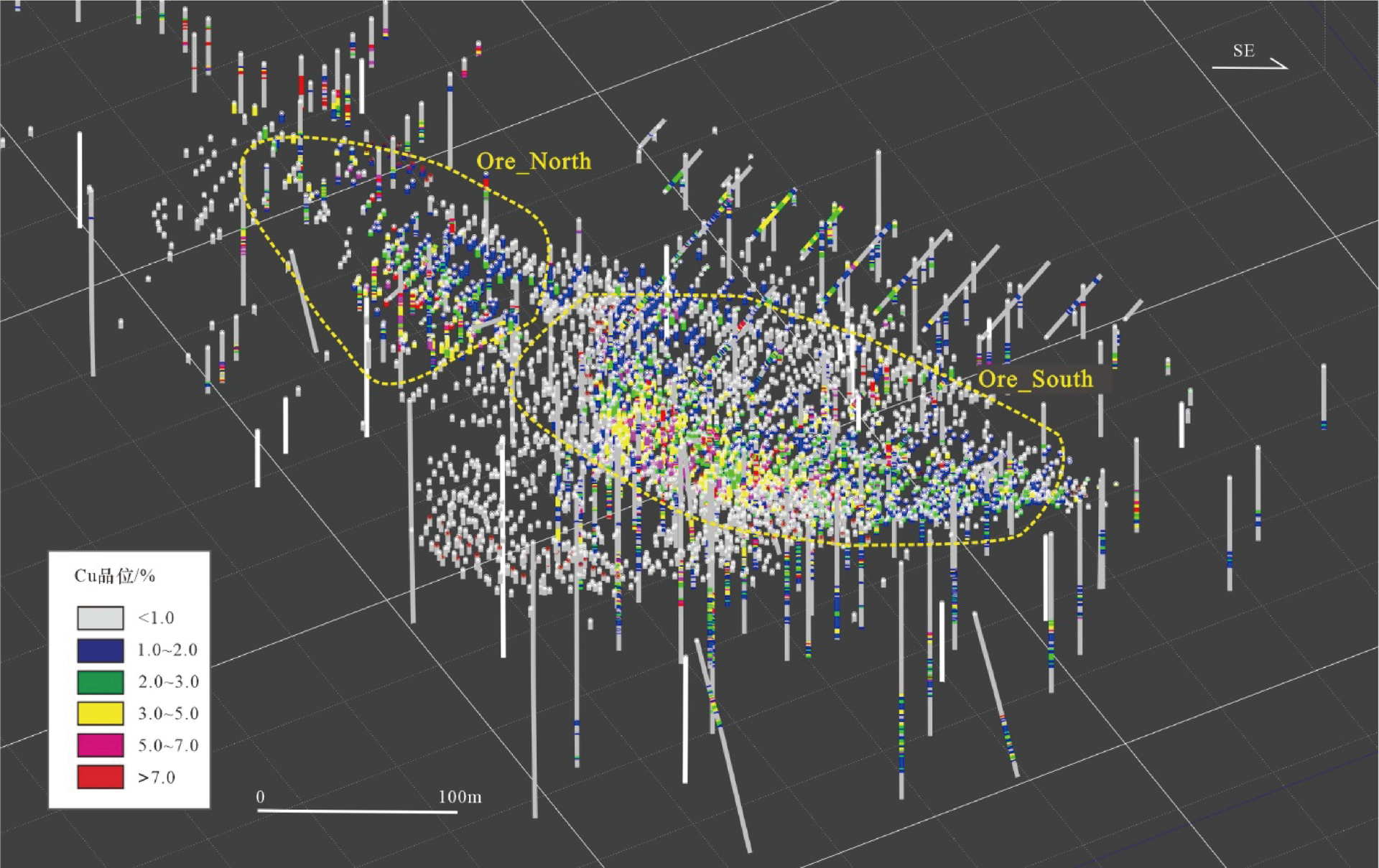
绿纱铜钴矿床位于刚果（金）东南部，比邻赞比亚。矿床产出受 NW—SE 走向绿纱 — 卡隆韦 （Luishia-Kalongwe）逆冲推覆体制约，矿体主要赋存于 Gris Roches Argillo-Talquoses（G. R. A. T.）、 Roches SiliceusesFeuilletées（R. S. F.）、Dolomites Stratifiées（D. Strat），部分Roches SiliceusesCéllulaires （R. S. C.）和 Shales Dolomitiques（S. D.）地层，少量脉状和透镜状矿化产于 Calcaires à Minerais Noirs （C. M. N.）地层。勘查工作控制主矿体长 1200 m，水平宽度 60~100 m，垂向延深约 150 m。矿体产状与地层相似，倾向 220°~240°，倾角 45°~55°。矿体铜平均品位 2.550％，钴平均品位 0.201％。NE 向断裂破碎带将矿体分为两部分。详查、补勘及炮孔数据见图4。按2 m基本取样样长，对原始勘查数据进行等长组合，组合后铜样品数据为 4560，最小值为0. 005%，最大值为29.53%，均值2.33%。

6.2 分形分析与矿化体圈定

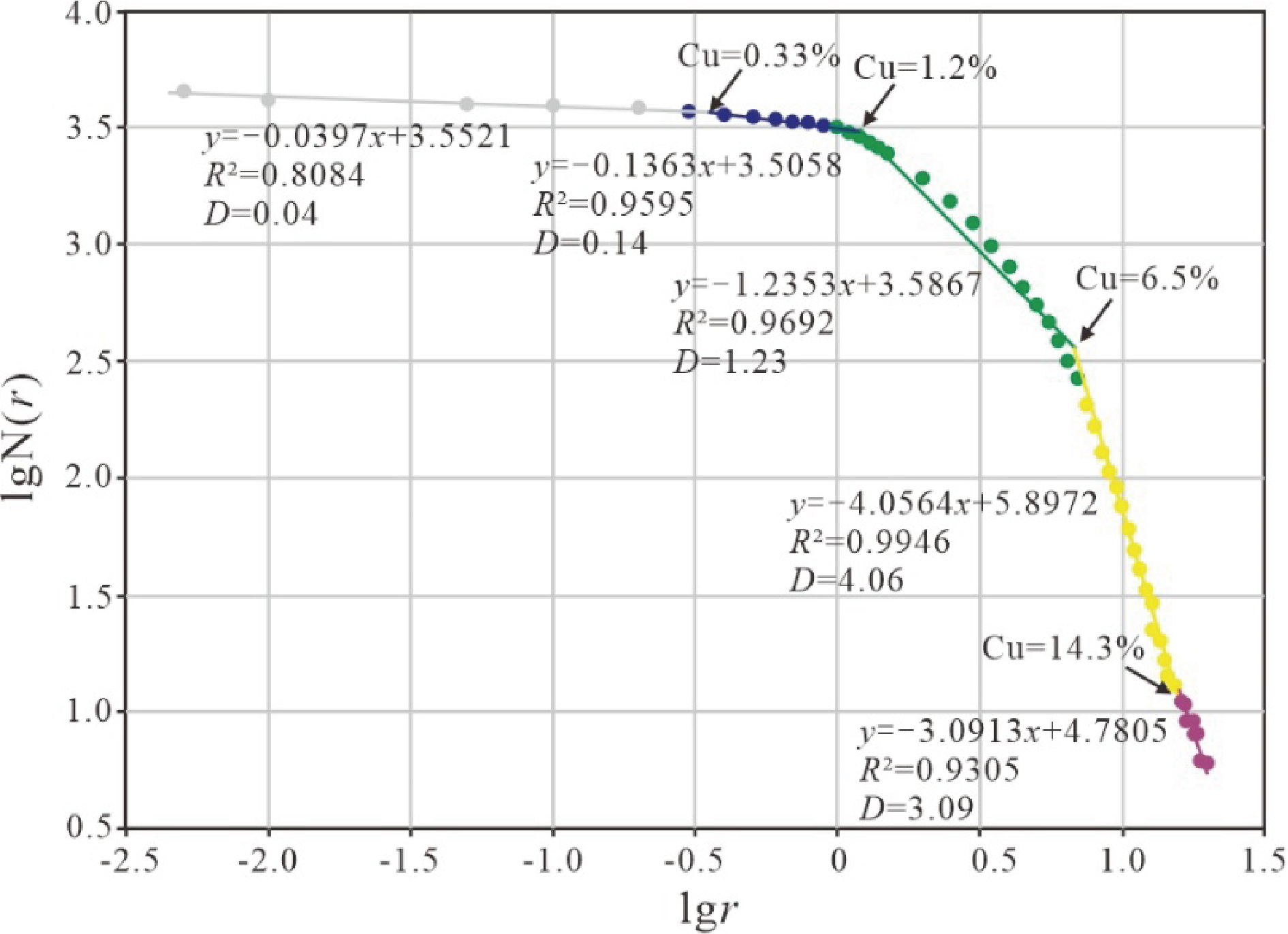
采用分形分析对主矿体的等长组合数据进行特异值处理，确定资源量估算的矿化域。从结果可以确定（图5），分形拐点分别为0.33%、1.2%、6.5% 和14.3%，矿化域范围为0.33%~14.3%。样品数据的特高值为 14.3%，特低值为 0.33%，高于 14.3% 的16个铜品位数据用14.3%代替。可以看出，在分形分布范围内，随着品位增高，分维值从 0.14 增加到 1.23 和 4. 06，表明样品点数据的空间相关性增强。

利用矿化边界品位 0.33% 圈定矿化体（未剔除夹石）。由于400线左右矿体为晚期Roches Argillo-Talquoses（R. A. T.）构造角砾岩所截断，将绿纱主矿体分为北部（记作 Ore_North）和南部（Ore_South）两个矿化体（图6），分开对南北两个矿化体进行圈定、统计分析、建模和估值。

统计结果表明，去特异值后Ore_North数据特征为，N=708，最小值 0. 03%，最大值 14.30%，均值 2.979%，方差 8.861，变化系数 99.9%；Ore_South数据特征为，N=3136，最小值 0. 029%，最大值 14.30%，均值 2.636%，方差 4.936，变化系数 84.3%。

lgr—不同边界品位r的对数值；lgN（r）—大于或等于边界品位r的样品个数的对数值

6.3 边界分析与估算域确定

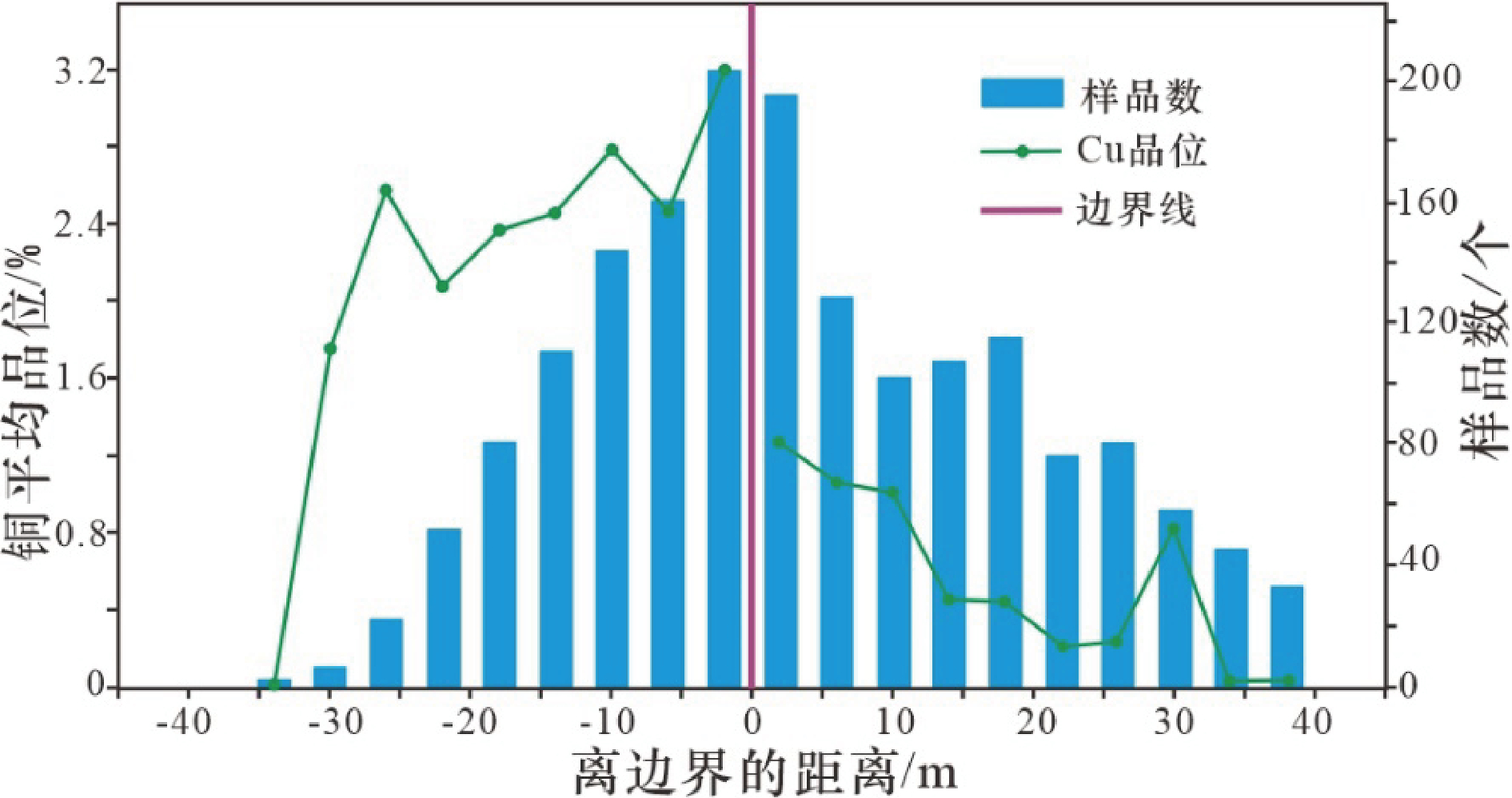
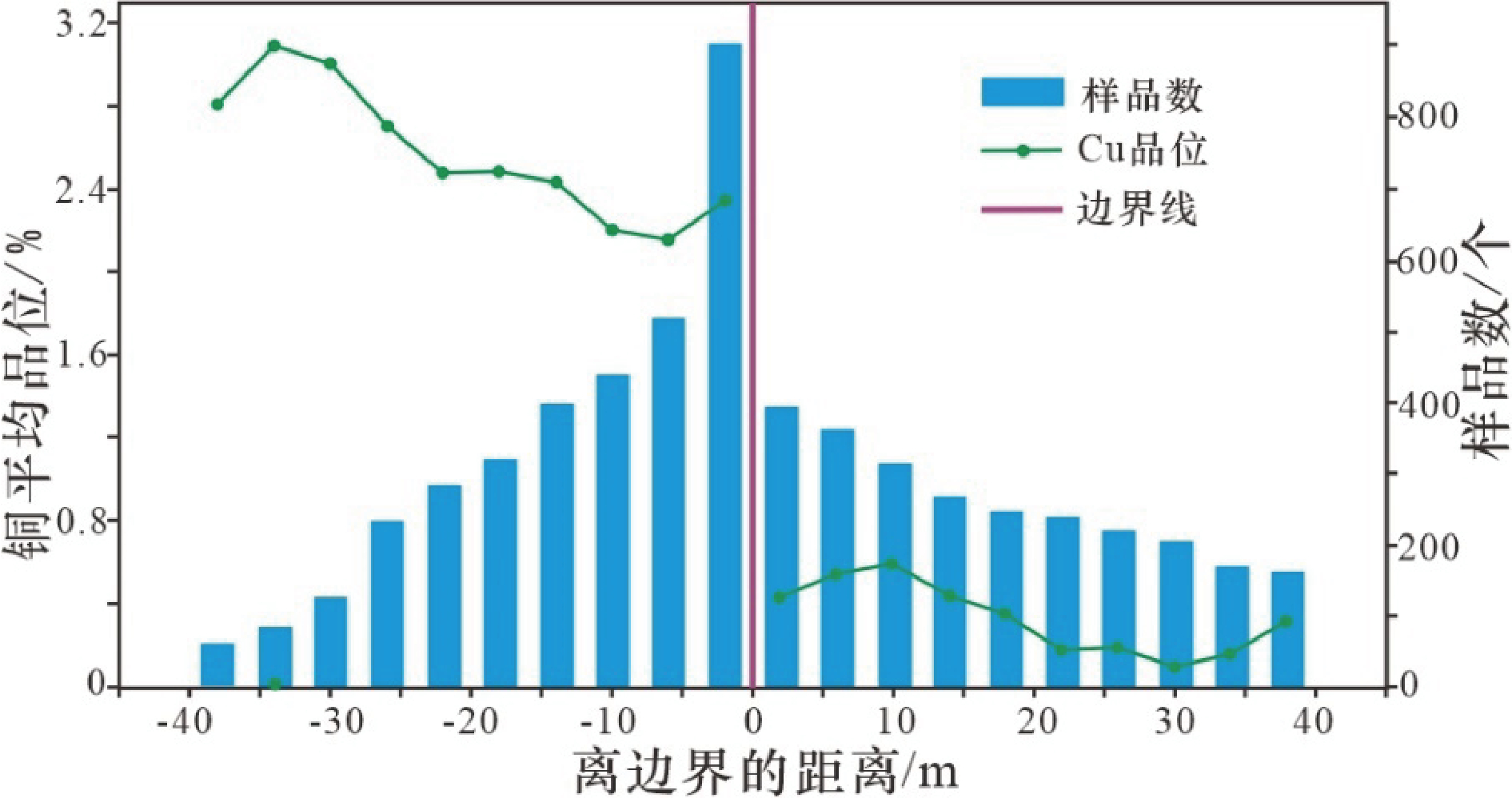
基于工业边界品位Cu=1. 0%进行边界分析，结果见图7 和图8。可以看出，Ore_North 边界内样品数据平稳，而外样品数据在边界附近呈现渐变过渡关系，呈现半软边界特征；Ore_South 边界内外样品数据变化截然，为典型的硬边界特征。因此，对 Ore_North 的估值可以采用域外一定范围内的数据 （0.33%~14.3%），而对 Ore_South 的估值仅采用域内数据（1. 0%~14.3%）。

6.4 变异函数分析与估值参数确定

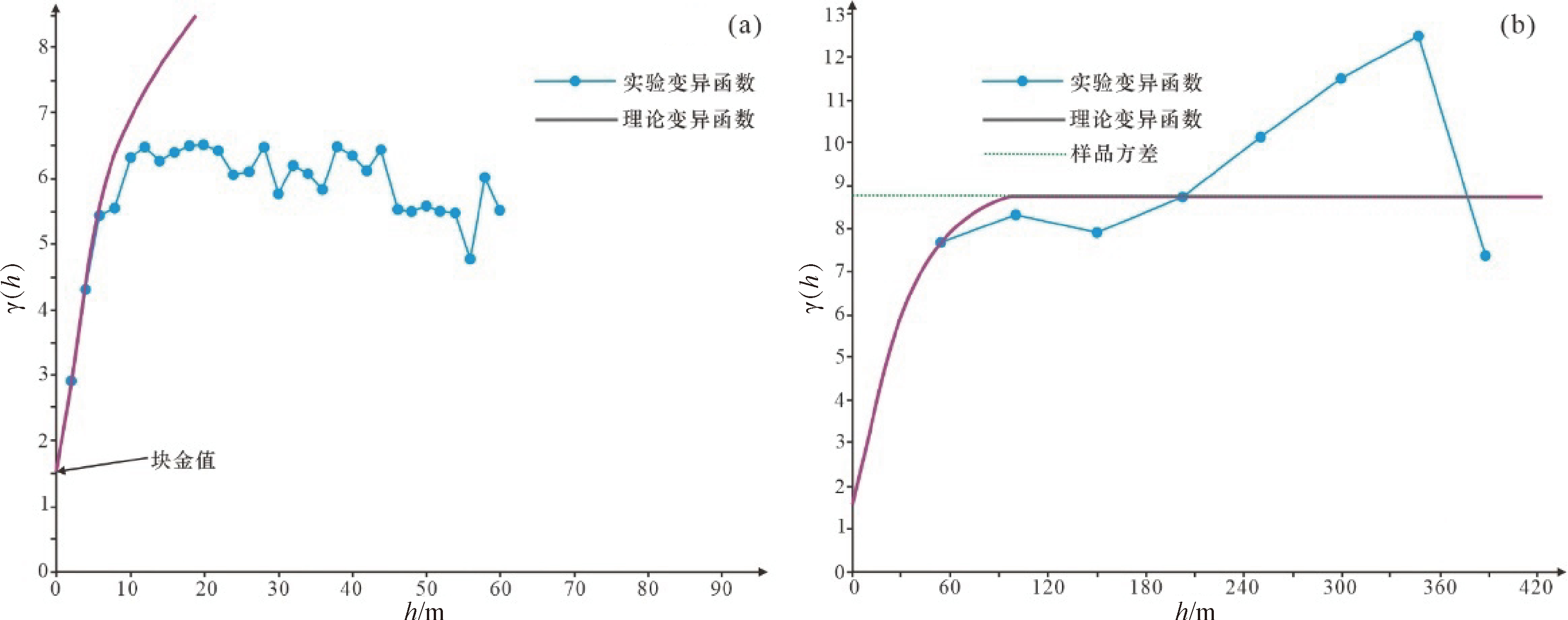
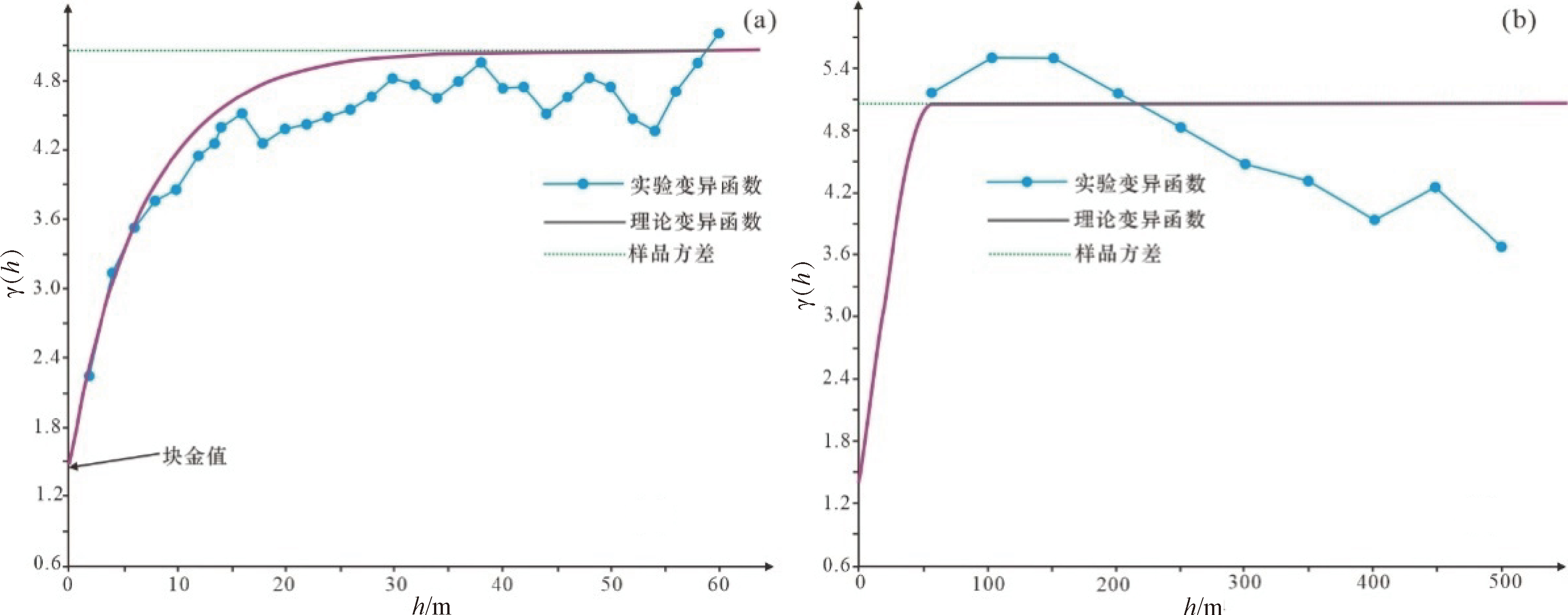
对南北矿化体样品数据进行井向变异函数和全向变异函数分析来确定块金效应和最优变程（图9 和图10）。实验变异函数的拟合结果表明， Ore_North变异函数块金值为1.47，块金效应为17% （图9a）；Ore_South 变异函数块金值为 1.42，块金效应为 28%（图10a）。南北两矿化体样品数据均呈现相对较高的块金效应，IDW估值幂次选2；二者全向变异函数均显示最优变程为 50 m（图9b、10b），在 IDW估值时选用椭球搜索半径为60 m。

6.5 IDW估值

根据绿纱铜钴矿体产状特征，设置IDW估值参数为，走向 320°，倾角 45°；长轴：中轴：短轴为 1∶0.23∶0.6；基本搜索半径 60 m，8 扇区，每区最多样品点 6 个，最少 3 个；幂次为 2。块模型估值结果见图11。

a—Ore_North样品数据井向变异函数分析；b—Ore_North样品数据全向变异函数分析

a—Ore_South样品数据井向变异函数分析；b—Ore_South样品数据全向变异函数分析

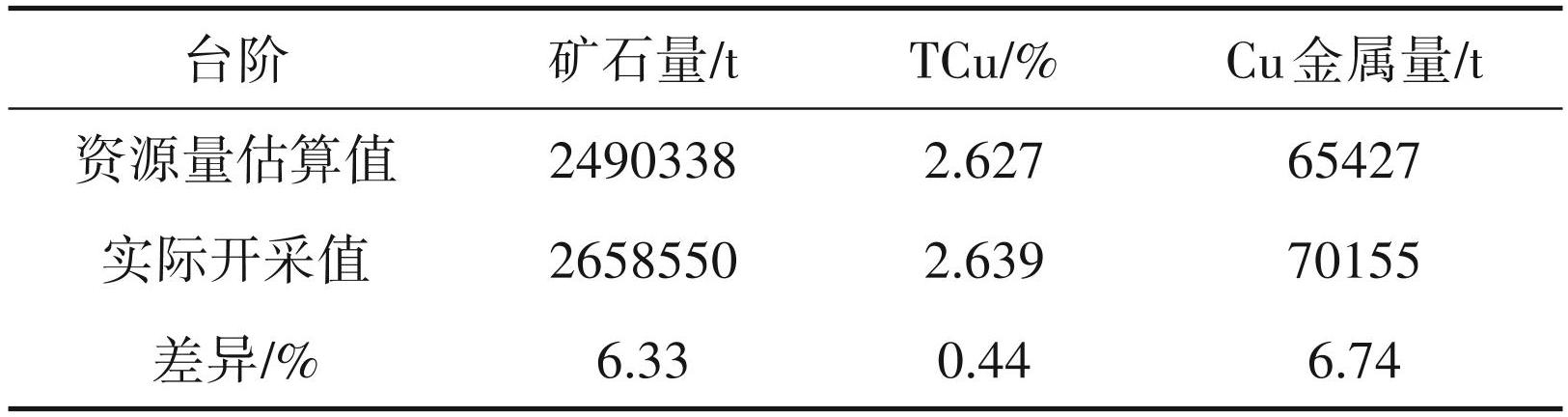
以 1% 作为工业边界品位，报告块模型中工业矿体的资源量。通过绿纱主矿体 1170 m 台阶探采对比（表1），采用改进方法估算资源量与实际采出矿量在铜矿石量、金属量、平均品位的差异分别为6.33 %、6.74%、0.44%，远低于规范 20% 标准，证明了改进IDW方法的可靠性。

7 讨论

本文基于矿块指标体系的IDW估值方法，引入分形分析、边界分析以及井向和全向变异函数分析，来定量化资源量估算过程及估值参数，深化了样品数据的地质特征、统计特征和经济属性之间的联系，也为块矿指标体系下估值方法及参数的确定提供了统计上的依据。

7.1 分形分析指示了矿化域圈定的临界品位值

分形分析提供了块矿指标体系下圈定矿化域的定量方法。分形分析基于样品品位数据的分形分布统计特征，通过类似混合总体筛分的方式，给出矿化域的边界品位值和特高品位值，来实现用于资源量估算的矿化域与“异常值”的有效分离。矿化边界品位分隔了矿化体和矿致异常，特高品位值则给出了矿化体品位的上限，二者为矿化域圈定的临界品位值。相对于规范推荐的确定矿化边界品位的方法，分形方法操作简单且更为稳定。例如，金属矿床的矿化样品数据多呈正偏态分布，如果运用直方图和累计分布曲线方法容易给出特高品位值，但难以给出矿化边界品位值；而分形方法可以同时给出矿化边界品位值和特高品位值（高帮飞等，2017）。

7.2 边界分析方法的实际应用

边界分析可以用于确定最终的估算指标体系。勘查规范对于采用IDW方法进行资源量估算，推荐了矿块指标体系和矿床工业指标两种体系方法。前者圈定矿化域进行品位估值，后者则直接圈定工业矿体进行资源量估算。规范指出（中华人民共和国自然资源部，2020），当矿体与围岩界线截然时，采用矿床工业指标圈定矿体是适用的；而当矿体与围岩呈渐变关系时，圈定矿化域的优点更突出。但是，规范并没有给出具体的判定方法。从边界分析方法的角度来看，尽管采用分形分析方法已经圈定了矿化域，但最终能否用矿化域内样品数据进行资源量估算，还取决于工业品位边界的边界条件。当工业品位边界为硬边界条件时，可以采用工业指标体系进行圈矿和资源量估算，也可以采用矿块指标体系方法，但圈矿边界品位应为工业品位而不能是矿化边界品位；当工业品位边界为软边界条件时，应采用矿块指标体系方法。前期的研究显示，硬边界条件下，圈定矿化域进行估值会导致资源量估算的矿石量增加而品位低估（高帮飞，2018）；软边界条件下，采用工业边界品位圈矿估值会导致矿石量减少和品位高估（陈伟康等，2022）。此外，本文第4 节的案例表明，边界分析方法还可用于判定氧化矿与硫化矿、工业矿体与工业富矿体是否需要单独圈定和估值。因此，基于边界分析方法的资源量估算，还可以为矿山开发的工艺技术方案及首采区的确定给出有益建议。

7.3 变异函数分析与估值方法和参数的选择

利用变异函数分析来半定量 IDW 估值的幂次和距离参数，其本质是基于井向变异函数确定的块金效应，来建立其与估值参数和估值方法之间的联系。一般地，块金效应越小，距离待估矿块较近样品点对距离较远样品点的屏蔽效应越强，即在对待估矿块进行品位估值时，距离较近样品点的贡献更大（高帮飞等，2021）。由于克里格权重系数大小受屏蔽效应影响较大，在块金效应小、屏蔽作用强的条件下，可以选择克里格方法进行品位估值；如果采用IDW方法，则可以通过高幂次（4~5）、缩小搜索半径（估值邻域）来实现较强的屏蔽作用，使品位估值结果与块金效应特征相符合。反之，在块金效应大、屏蔽作用弱的条件下，优先采用IDW方法，通过低幂次（1~2）、扩大搜索半径（估值邻域）来降低屏蔽作用。

8 结论

本文重点论述了改进 IDW 估值新方法的关键技术，并在绿纱铜钴矿床资源量估算中进行了应用。改进的 IDW 估值新方法，综合运用分形分析、边界分析和变异函数分析，为资源量估算提供了新的思路，减少了人为干扰，提高了估值过程的定量化水平，也为矿块指标体系下估值方法及参数的确定提供了统计上的依据。下一步研究工作中，应深化上述统计方法与样品数据的地质特征之间的联系。例如在确定矿化边界类型时数学方法只是统计意义上的佐证，还需要补充完善地质填图与勘查工程编录资料支撑。此外，改进IDW方法与传统距离幂次反比法和普通克里格方法的估值结果对比，也需要在今后工作中进一步加强，以期更加说明新方法的先进性与可靠程度。

参考文献