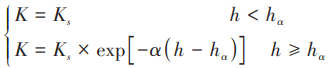-
0 引言
-
地质调查工程中发现,雨水渗透诱发的滑坡是自然界中严重的灾害之一(Froude and Petley,2018; 刘利嘉等,2021;刘秋强等,2021;Yang et al., 2021),因此对边坡的生态防护及支护工程显得尤为的重要(黄涛等,2004;闫新亮等,2019;陈冠一等,2022)。毛细管屏障(Capillary barrier)的结构常用来做诸如垃圾填埋场类的缓冲层,使入渗的雨水能顺着屏障层流出(Tojo et al.,2010)。由于两层土壤保水性能的差异,从地表渗入的水在两层土体的交界处被阻拦,当土体倾斜时,则沿着土体边界流下,而加固性能往往通过 CB导流的极限长度展示。在已有的关于 CB 极限长度的研究中,试验是在两层中进行的,上层是砂土,下层是砾石,主要目的是还原雨水入渗的过程,进而了解 CB 的基本特性 (Steenhuis et al.,1991;Miyazak,1995)。前人往往通过改变降雨强度和土层边界面的坡度,利用室内大土槽进行了极限长度的测量试验,随后进行结果分析并与经典研究中提出的两层 CB地的极限长度估算公式进行对比(Jian et al.,2013;Kobayashi et al.,2019;王家琛等,2021)。而将该方法应用于实际结构物时,通常会从底部建造一个砾石层和一个细砂层,随后至少添加一个保护层。然而,此类研究并未具体指出极限长度预测公式的适用范围,并且该预测公式没有考虑土层厚度的影响,因此结果无法对危险侧的极限长度进行预测。另外,当前对于三层覆土结构的加固效果及极限长度的预测尚且缺乏。
-
本文针对两层 CB 土层结构(下层砾石层和上层砂土层),通过不同层厚的大型土槽试验得到极限长度,定量评价了砂土层的层厚对降雨入渗控制功能的影响。此外,还根据试验结果进行了三层覆土结构的大型土槽试验,以此明确极限长度的预测公式必要的覆盖层厚度,并讨论了极限长度预测公式的应用方法。
-
1 CB极限长度
-
1.1 CB极限长度的定义
-
由于砂层和砾石层的保水性及渗透性的差异,从地表渗入的水被储存在砂砾层的分界面上(图1)。如果砂层和砾石层的交界处是倾斜的,积聚在砂层中的水将沿着倾斜的分界面向下流动(图1d)。随着雨水浸透整个边坡,集积流的水量也会随之增加,造成含水量增加,拟饱和区在分界附近的砂层中扩大。当砂层不能再容纳更多水时,从地表渗入的水开始渗入下部的砾石层,砾石层会突破拟饱和渗透线,达到图1e的状态。由雨水渗透而产生的集积流,其出现的位置与第一次发生突破位置之间的水平距离称为极限长度(Stormont,1996)。由于降雨或振动的影响,构成 CB 的上部砂层会移动到下部砾石层,为了保证 CB的极限长度,砂层和砾石层粒度之间的配比显得非常重要。简述入渗过程即是:在细粒土层和粗粒土层组成的不同上部结构厚度下,随着雨水的不断渗入,到达砂砾层交界处时渗透线开始倾斜,当雨水突破渗透线到达砾石层时,渗透线达到最大倾斜的同时 CB 就出现极限长度。
-
图1 降雨入渗示意图
-
1.2 CB极限长度的预测公式
-
关于 CB 极限长度,Kung(1990)、Ross(1991)和 Steenhuis et al.(1991)基于材料性质(透水性和保水性)、结构因素(层交接面倾角)和外部因素(降雨强度)等,分别提出了适用的极限长度预测公式。而随后的学者通过大量试验证实 Steenhuis et al. 提出的预测公式精度更高(Stormont,1996;Jian et al., 2013;Kobayashi et al.,2019),提出的极限长度预测公式在q<<K的条件下由式(1)表示:
-
式(1)中,L 为 CB 极限长度(cm),q 为渗透流量 (cm3 /s),Ks为上层土层的饱和导水率(cm/h),φ为层边界面的倾角(o),hα 为上层样品的空气侵入值 (cm),hw为下层的水样本渗透值(cm),α为上层土层的非饱和导水率K用h的指数函数近似时的系数,h 为水头高度(cm)。此外,式(1)中的α为:
-
排水过程的土水特征曲线(SWCC)基于 Genuchten and Th(1980)模型(V-G 模型)。非饱和导水率可以用模型的参数来预测,在本试验中,α被设定为0.12。
-
Steenhuis et al.(1991)提出的极限长度预测方程是在Ross方程的基础上优化得到的,在确定非饱和导水率时考虑了砂的空气渗透值 hα和砾石的水渗透值 hw。其中空气渗透值是指饱和土的压力头降低,空气首次进入时的压力头,水渗透值是指向非饱和土加水,大部分空气被排出,孔隙中的水基本连续时的压力头。
-
2 CB极限长度评估试验
-
2.1 试验材料
-
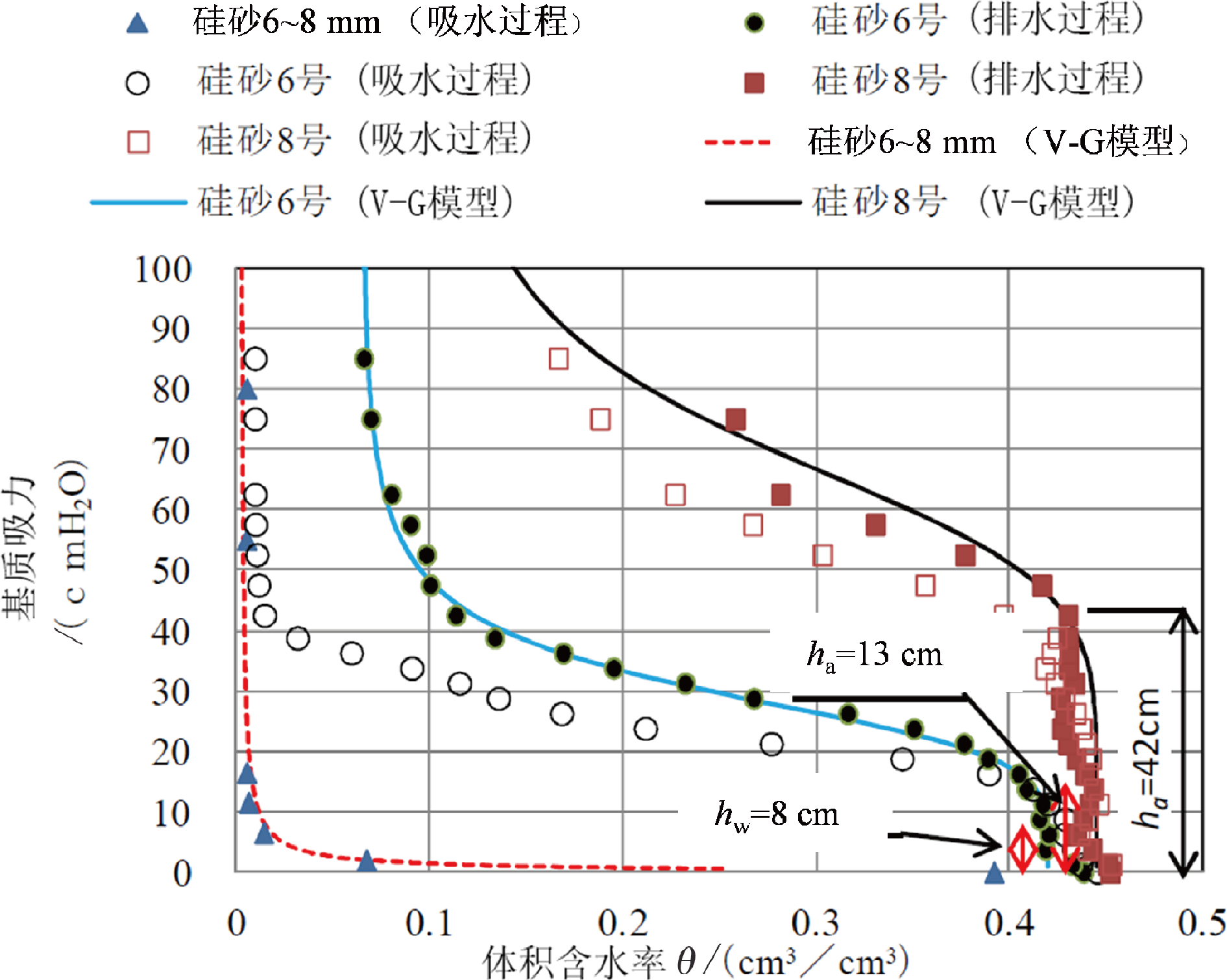
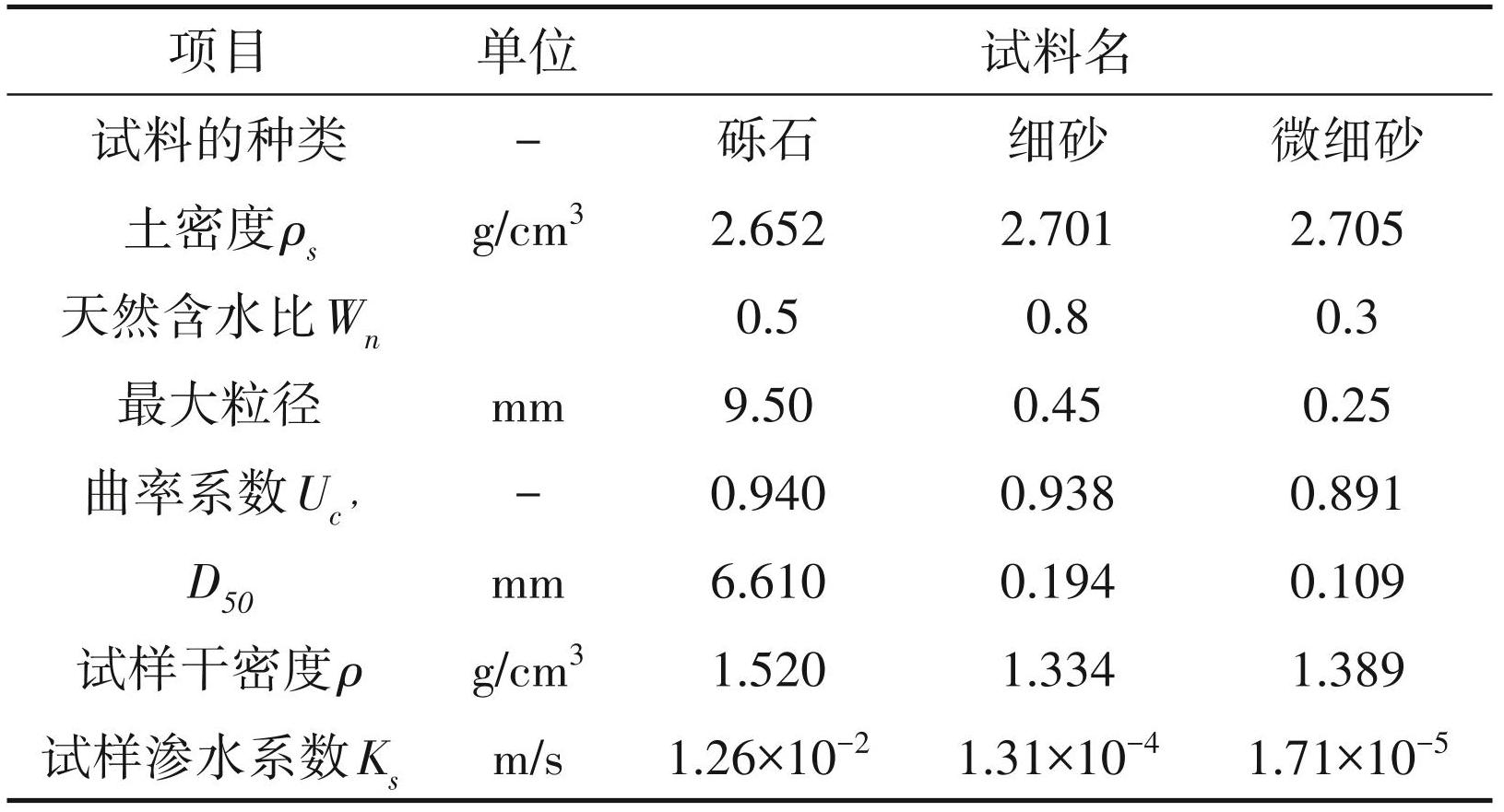
表1为测试样品的物理特性。从表中可得知选取的砾石为 6~8 mm 的硅砂,细砂材为硅砂 6 号,微细砂为硅砂8号,同时详细列举了各试料的粒径、曲率系数和试样渗水系数等参数。在大型土槽试验中,下层土壤(碎石)为 6~8 mm 的硅砂,上层土壤 (细砂)为 6 号硅砂。采用土柱法求得土壤保水性,试验结果如图2 所示。在图中,空气和水的渗透值是由垂直上升高度计算得来,其中体积水含量在饱和区域无变化。研究将保水试验和土层制备所用的砂料调至最佳含水量(6 号硅砂 11.9%,8 号硅砂 19.8%),砾石料的天然水分含量比 0.5%。试验中为试件和大型土槽试验准备土层时,已静压至干密度(压实度为90%)。
-
2.2 测定CB极限长度的试验装置
-
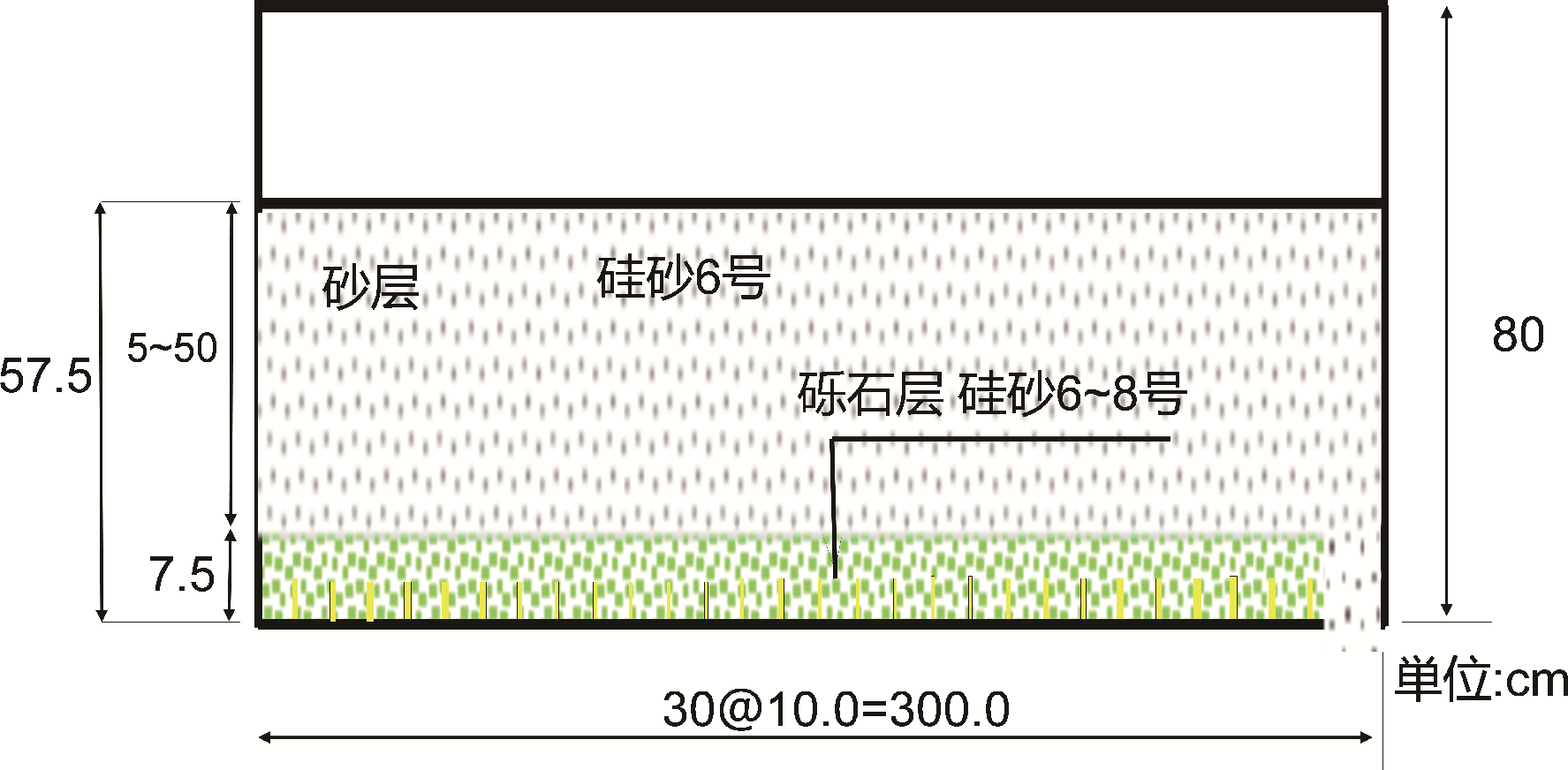
图3为用于两层CB地基试验的大型土槽,土槽高80 cm,深20 cm,宽300 cm。在土槽底部,每隔10 cm 放置一块 3 cm 高的隔板,以便密切监测发生突破的位置。通常极限长度是指从上层到下层发生突破的层间边界的水平长度,但由于在土槽试验中无法确定突破的确切位置,所以本文中极限长度是指首次观察到径流的出口处的水平长度。此外,在每个隔板的下游端设置一个出口,这样就可以每隔 10 cm测量由砂层渗入砾石层的径流量。在土槽的下游端底部设有排水集水区,能让只流过上层土壤 (细砂材料)的水顺畅地排到外部。
-
图2 砂石的SWCC曲线
-
图3 两层CB地基的试验装置
-
在大型土槽的上部,安装了一个水箱(尺寸:高 70 cm,深 20 cm,宽 300 cm)作为降雨装置。将注射针头(内径 0.3 mm)以 5 cm 的间隔放置在水箱底部,直接向表面降雨。降雨强度(mm/h)通过将水箱中的水位保持在指定的高度来控制。
-
首先用砾石填满土槽,将已测量质量的样品放入土槽中,使干密度达到预定值,然后用木制夯板 (5 cm×5 cm)将整个砾石层静态压实到 7.5 cm 厚。然后在两种土壤的交界面上安装厚度为0.13 mm的无纺布,使上部填充的砂层不会混入两者之间的间隙。用手工制作的夯板将砂层缓慢地静态压实到5 cm的高度,之后将测量好质量的样品放在一个大的土壤罐中,以达到规定的干密度。对每层土壤重复此工作以制备厚度为 10~50 cm(5 cm/层,2~10 层饰面)的砂层。
-
2.3 试验条件
-
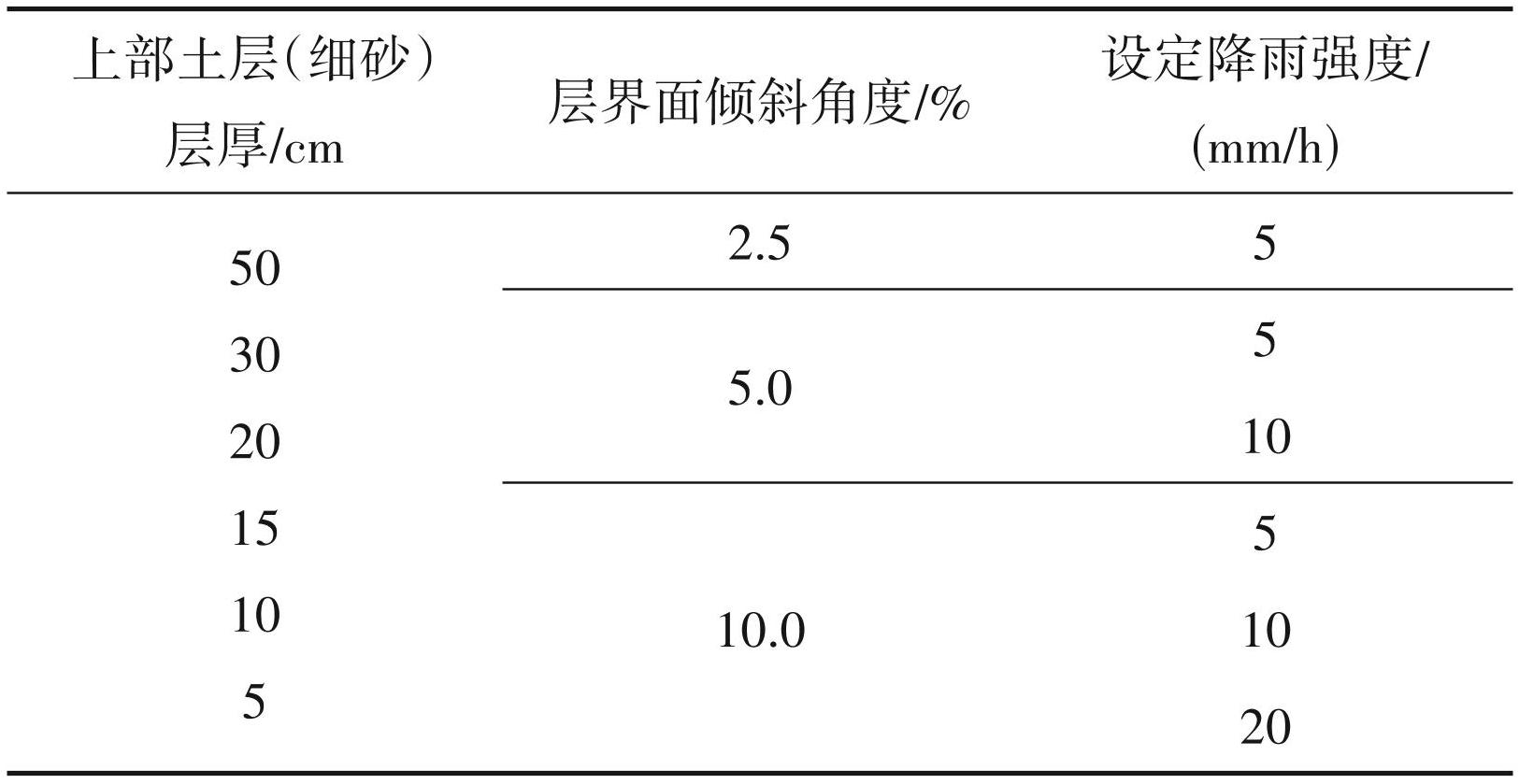
此次试验总共设置了31种条件,其中上层土层 (细砂)的厚度为 10~50 cm,每层厚度的土层边界坡度和降雨强度相应组合(表2)。在确认总径流等于稳定状态后的总供水量后,对每组试验底部的径流量进行测量。首先,用 1 L 的烧杯收集从出口流出的流出物,10 min 内的流量被重复测量 3 次。在完成对径流体积的测量后,目视观察每个出口的径流状态,并测量从上游端到最靠近出口的突破点以及可以看到径流的斜向距离,完成试验。
-
2.4 二层CB极限长度结果
-
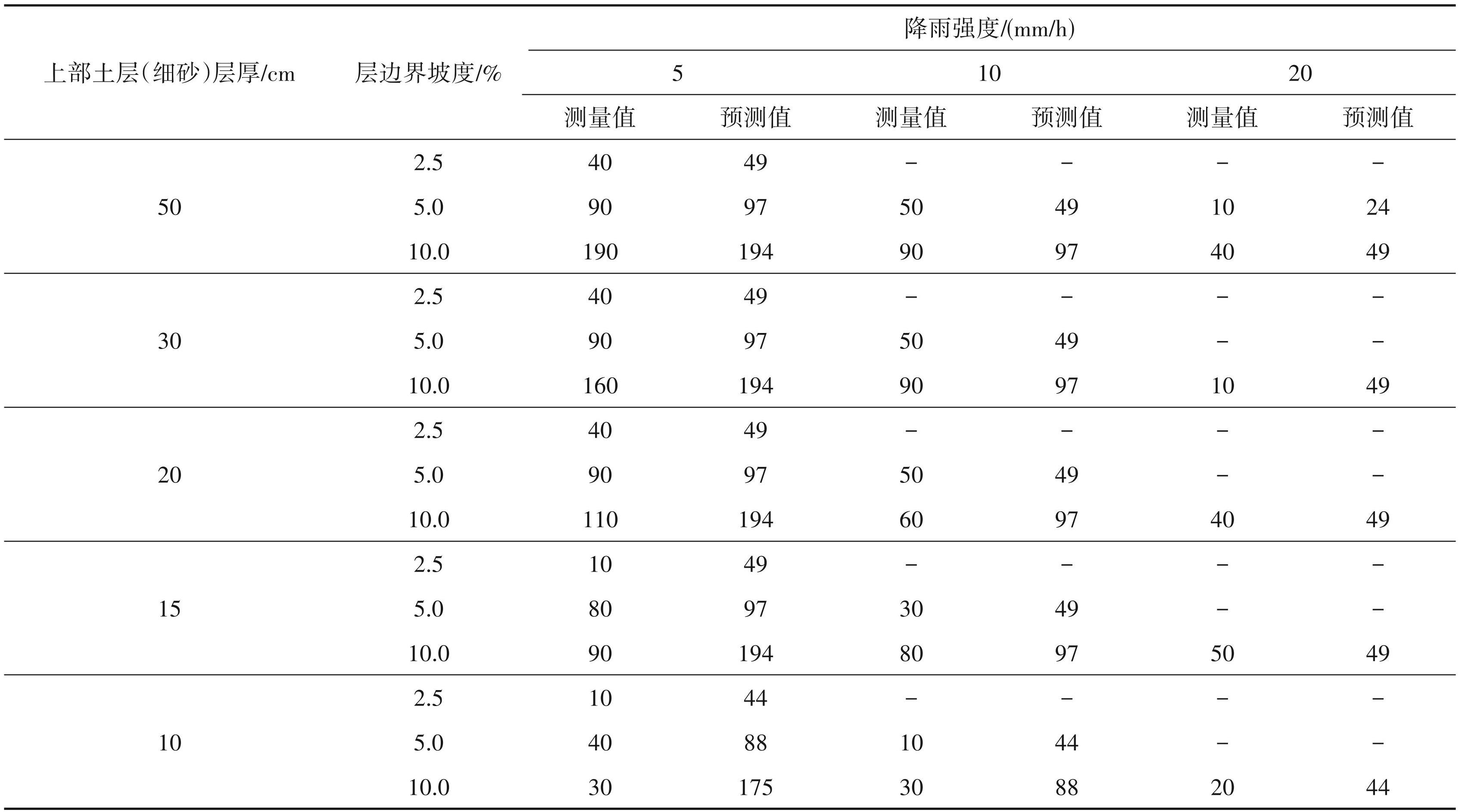
每组试验中测量的 CB地基的极限长度见表3。每个极限长度都是基于土层界面(土槽)的坡度角,将试验的斜向距离转换为水平距离得到。表中显示的预测值是由 Steenhuis et al.(1991)提出的极限长度预测公式(1)得到。代入式中的通量 q,是根据每个试验案例在稳定状态下的实际径流量计算出来的实际降雨强度。如表3 所示,在相同的坡度角和降雨强度下得到的极限长度(测量值和预测值) 往往随着上层土壤厚度的减少而产生很大差异。但是,由于隔板以 10 cm 的间隔进行安装以收集流入该部分的水,以及土壤罐的性能不同,测量结果可能会出现约±10 cm的差异。
-
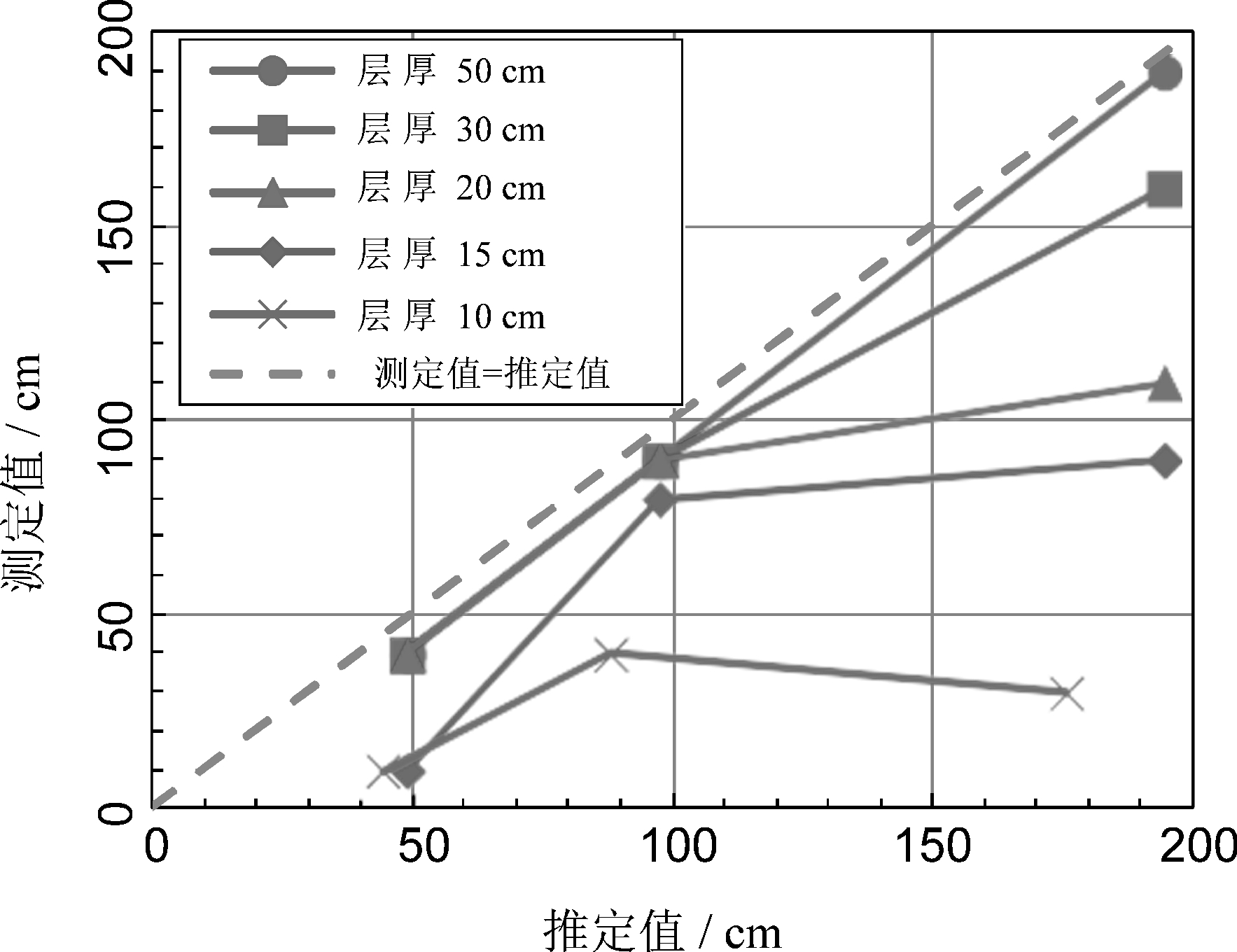
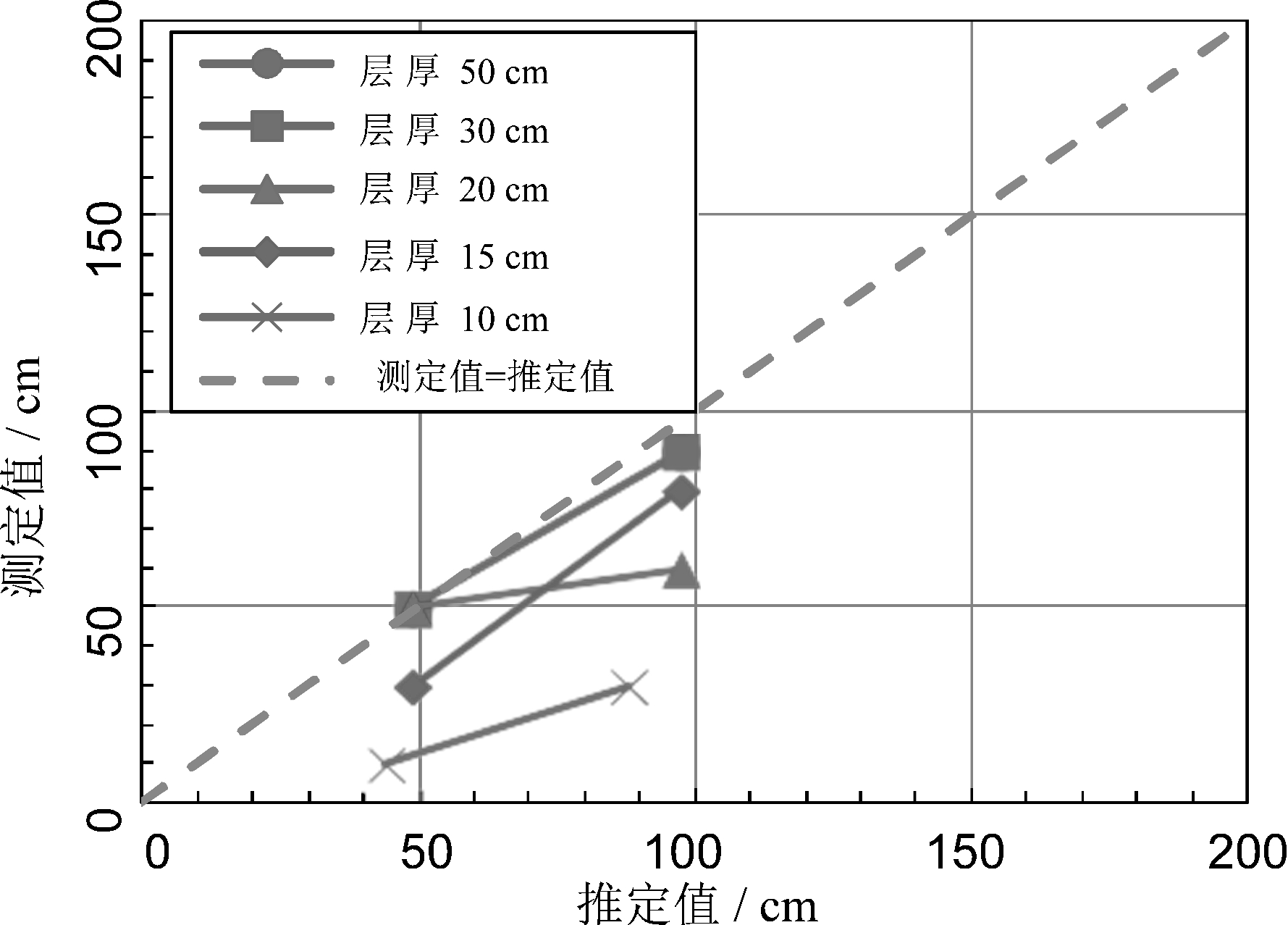
图4~图6为表3中所示的每个降雨强度对应的极限长度值(预测值和测量值)。图4显示了在降雨强度为5 mm/h的情况下,改变上层土壤厚度而产生的结果。如果该层厚度为 30 cm,极限长度的测量值与预测值基本相同,但即使在这种情况下,测量到的极限长度也会随着坡角的增加而趋于减少。当层厚<20 cm 时,极限长度的测量值往往比预测值要短。
-
图4 极限长度比较(降雨强度5 mm/h)
-
图5 所示在降雨强度为 10 mm/h 的情况下,当水层厚度不超过约 30 cm 时,极限长度的测量值有变短趋势。层厚为 10 cm 的测量值最小,与预测值的差距最大,相比来看层厚为 30 cm 的测量值与预测值基本吻合。
-
图6 所示在降雨强度为 20 mm/h 时,尽管层厚有一些变化,层厚为 50 cm 时的极限长度与预测的极限长度基本相同,这表明所需的上部土层厚度随着降雨强度的增加而增加。然而,如果该层厚度小于空气渗透值ha,在应用公式(1)时,该层厚度被视为空气渗透值ha。
-
图5 极限长度比较(降雨强度10 mm/h)
-
图6 极限长度比较(降雨强度20 mm/h)
-
综合以上结果可以得出,前人给出的极限长度估算公式即使考虑到试验条件范围内的降雨强度问题,也可以适用于50 cm的土层厚度,不过当使用 6 号硅砂作为上层土时,至少要有一个空气渗透值的厚度。研究认为,低于 30 cm 厚度的真实值可能较小,因为 30 cm 极限附近的数据往往包括了土槽边界(下游)的影响。除此之外,这些试验的上层土层厚度薄至 20 cm,也可能是试验数据被低估的原因之一。
-
3 三层CB极限长度评估试验
-
3.1 试验说明
-
为了将已应用于两层 CB 地基试验的极限长度预测公式推广到三层 CB 地基的试验结果,研究进行了三层 CB地基的大型土槽试验。同时对认为必要的上部土层(细砂层)的层厚进行评价,讨论了应用极限长度预测预测公式的方法。
-
3.2 试验材料
-
三层 CB 试验所用样品为 6~8 mm 硅砂,下土层样品为砾石料,6 号硅砂用于中层土壤,8 号硅砂用于上层土壤。
-
3.3 测定CB极限长度的试验装置
-
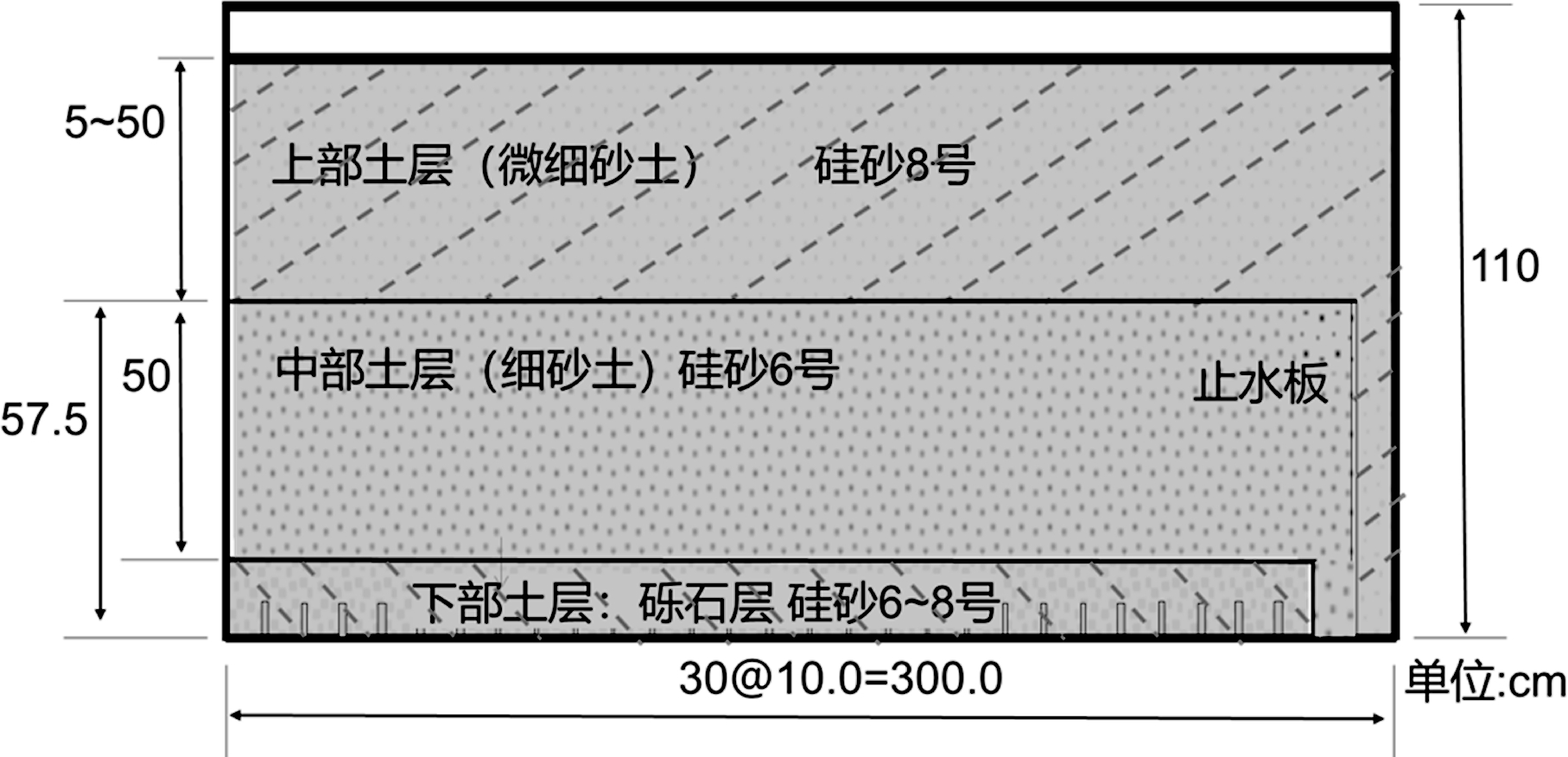
图7 为用于三层 CB 地基试验的试验装置。土槽高 110 cm,深 20 cm,宽 300 cm。降雨装置与 2.2 中所示的装置相同。
-
图7 三层CB地基的试验装置
-
3.4 试验条件
-
试验如表4 所示,中层土层厚度设为 50 cm 不变,通过改变土壤覆盖层对应的上层土层样品(细砂料)层厚,并结合各层厚度的交界倾斜度和降雨强度,总共进行了36组试验。各组试验槽底径流量及斜距测量方法同上一节。每组试验的稳态出水量在不同时间测量了 3 次,但由于得到的出水量及其分布几乎相同,图中显示了3次的平均值。
-
3.5 试验结果和分析
-
研究发现,随着水箱坡度的减小和降雨强度的增加,在稳定状态下观察到径流的出水口量增加 (Walter et al.,2000;Zhan et al.,2014)。在这种情况下,发生一次突破,大量水渗入下部土层,使 CB 功能恢复,渗入水再次形成积聚流,并发生了另一个突破。这种趋势在层厚为30 cm时也发生了。
-
图8显示了 50 cm和 30 cm层厚的渗透率,虽然降雨强度和倾斜角度没有恒定的趋势,但70%~90% 的渗透率较低,且渗透率平均值为 82%,平均偏差为0. 04。
-
图8 中部土层(细砂层)的渗透率分布
-
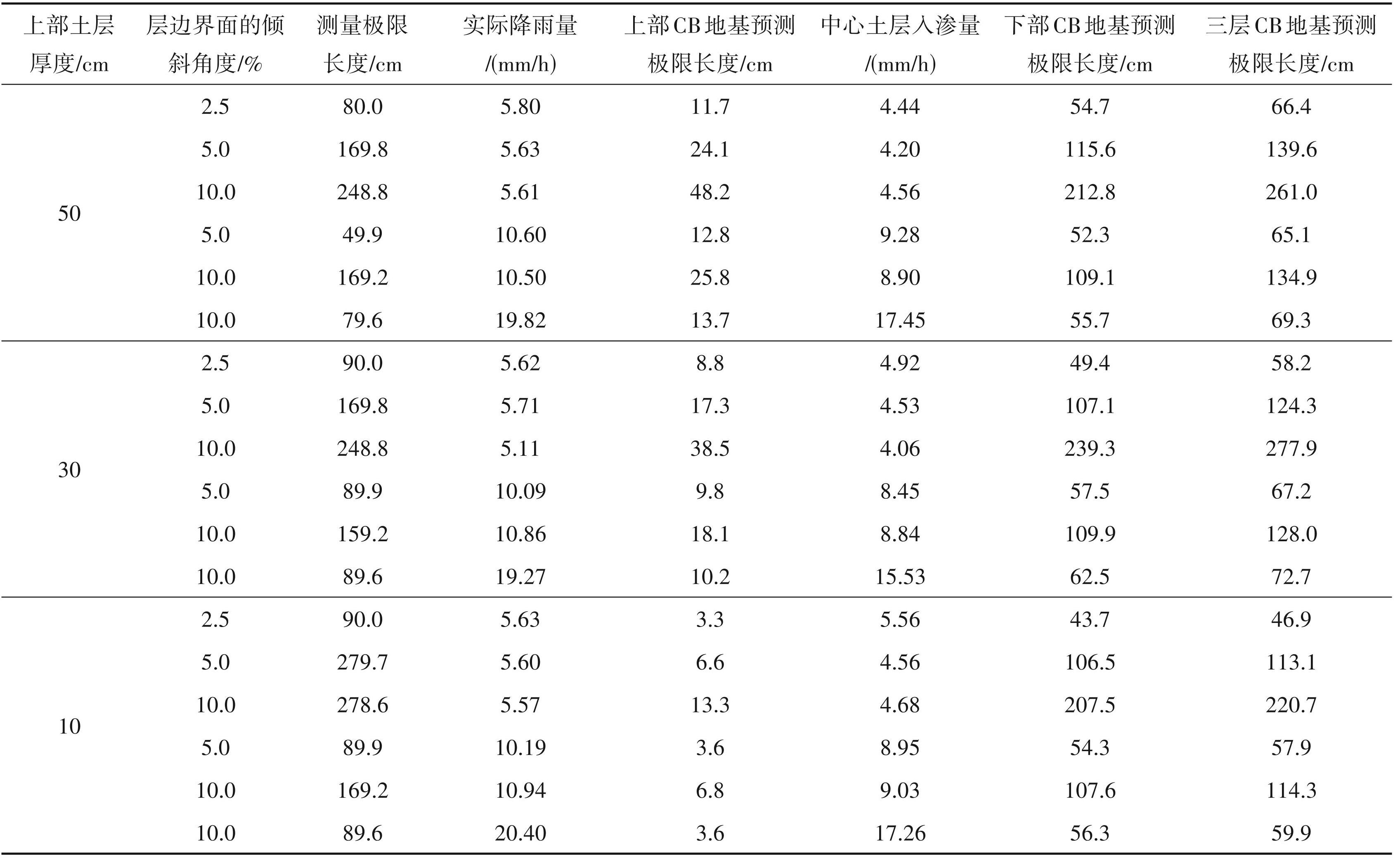
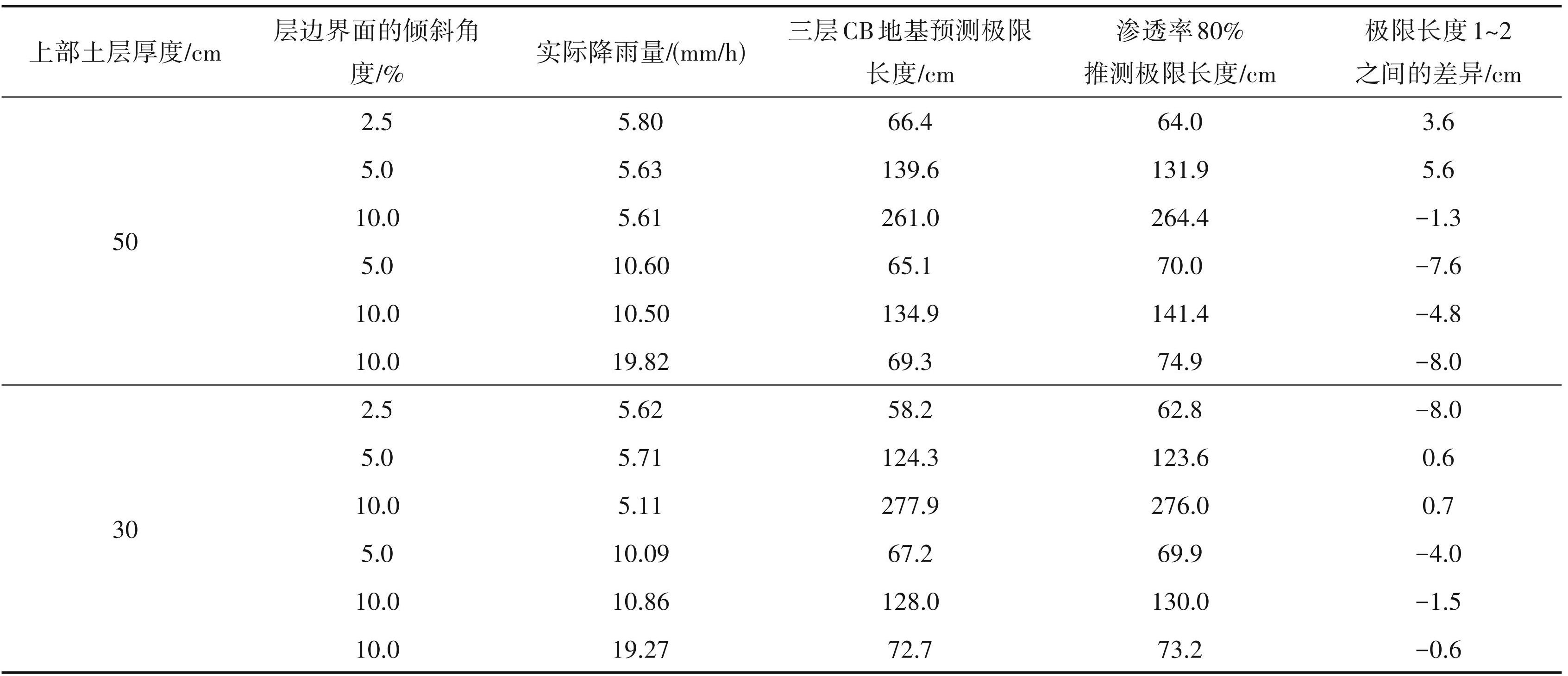
表5 为通过对试验中的斜向距离进行校正,将其转换为水平距离得到了 CB的极限长度和预测的极限长度。三层 CB 地基的估算极限长度是利用 Steenhuis et al.(1991)提出的CB极限长度估算公式得到,同时考虑上层土层和中层土层的上层 CB 地以及中层土层和下层土层的下层 CB 地的值。表6 说明了极限长度计算的流程,该层厚度为 50 cm,倾斜角为 2.5%,实际喷水强度为 5.80 mm/h。试验得到的测量极限长度是 80. 0 cm。根据公式计算,上层 CB 地(8 号硅砂和 6 号硅砂)的极限长度为 11.7 cm。此外,如果将方程应用于下层 CB 地(6 号硅砂和 6~8 mm 硅砂),使用 4.44 mm/h 的渗透通量进入中间土层,极限长度为 54.7 cm,三层 CB 地的总预测极限长度为 66.4 cm。同样的方法被用来计算三层 CB 地的预测极限长度。代入公式(1)的渗透通量 q,是根据每个试验案例获得的稳定状态下的实际径流量计算出的实际降雨强度。然而,进入上层土层的渗透通量可以通过降雨强度来获得,而进入中层土层的渗透通量应该由上层土层发生突破后进入中层土层的渗透量来获得。因此,我们将中间土层的渗透通量定义为流入出口缩水区的径流。
-
当应用经典公式来估算有土壤覆盖的三层 CB 土的临界长度时,如果上层土壤使用低渗透性(如 1. 0×10-5 cm/s)的淤泥质黏土(Ks<q),所施加的水 (2.78×10-4 cm/s)超过了渗透能力(1. 0×10-5 cm/s),一些不能渗透的水会通过表层流下来。渗透通量受到上层导水率的限制,超过导水率的水不能渗入。在这种情况下,最大的渗流通量可以被认为是淤泥质黏土的导水率 Ks(1. 0×10-5 cm/s),但是 Ks的值非常小,当应用极限长度方程时,将是 1 cm 或更小的数量级。这意味着,如果上层土壤是淤泥质黏土,导水率为1. 0×10-5 cm/s,就不会出现CB,也不需要考虑极限长度。如果期望淤泥质黏土和砂土层的组合具有 CB 功能,那么上层渗流应该足够小。使用低渗透率的黏性土作为土壤覆盖层的优势不是 CB功能,而是控制和减少渗透通量,这导致在较低的 CB 处有较长的极限长度。由于 q<<Ks 不被极限长度方程所满足,考虑到进入中间土层的渗透通量,这种情况下,上覆土壤的导水率Ks,只需考虑中间和下层土壤的CB。
-
在上部土层为细砂的情况下,只要满足条件q<<Ks,上层和中层土层以及中层和下层土层的 CB函数就可以应用经典公式,来考虑各层的非饱和特性和上述各层的渗流量。
-
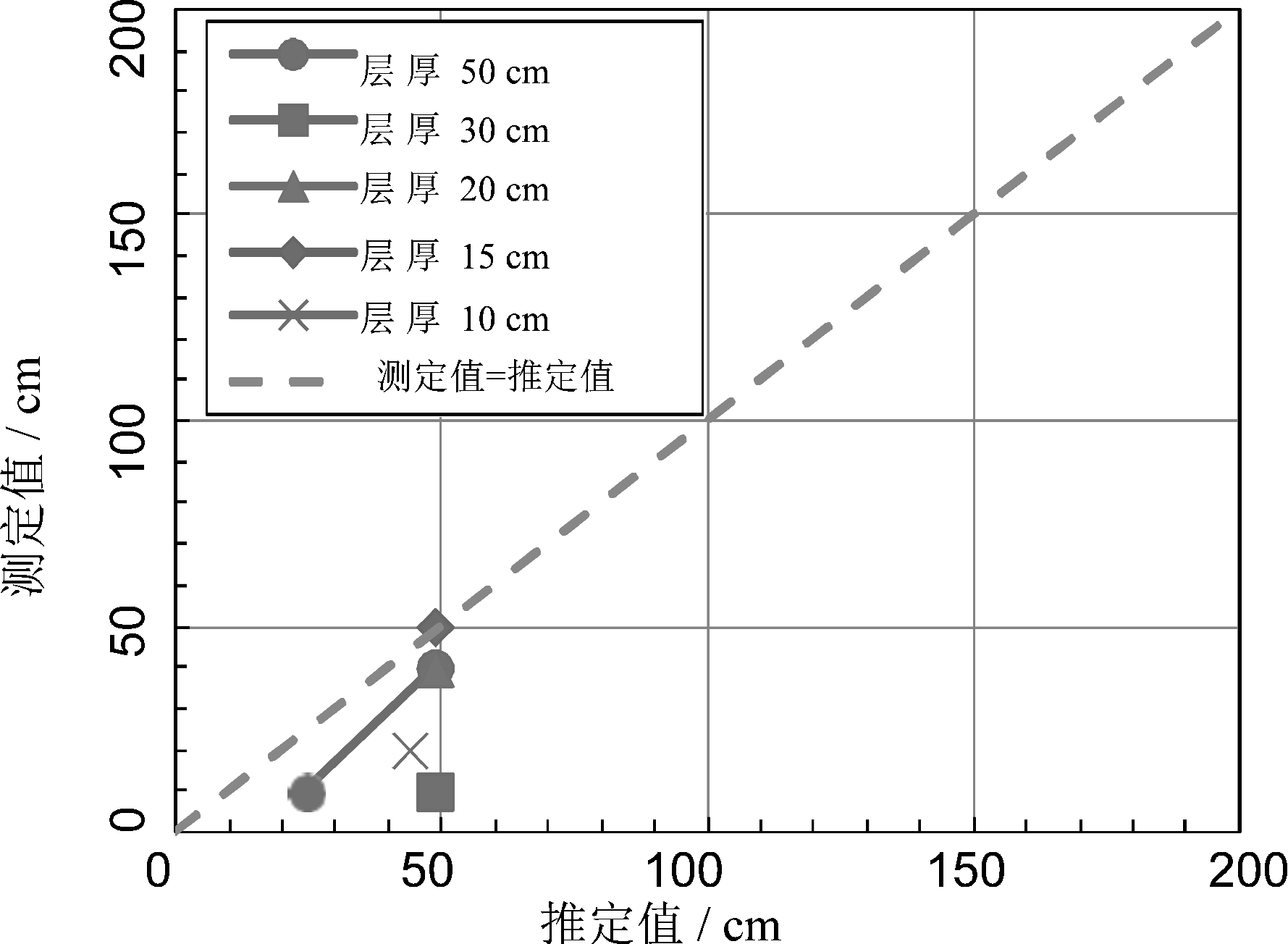
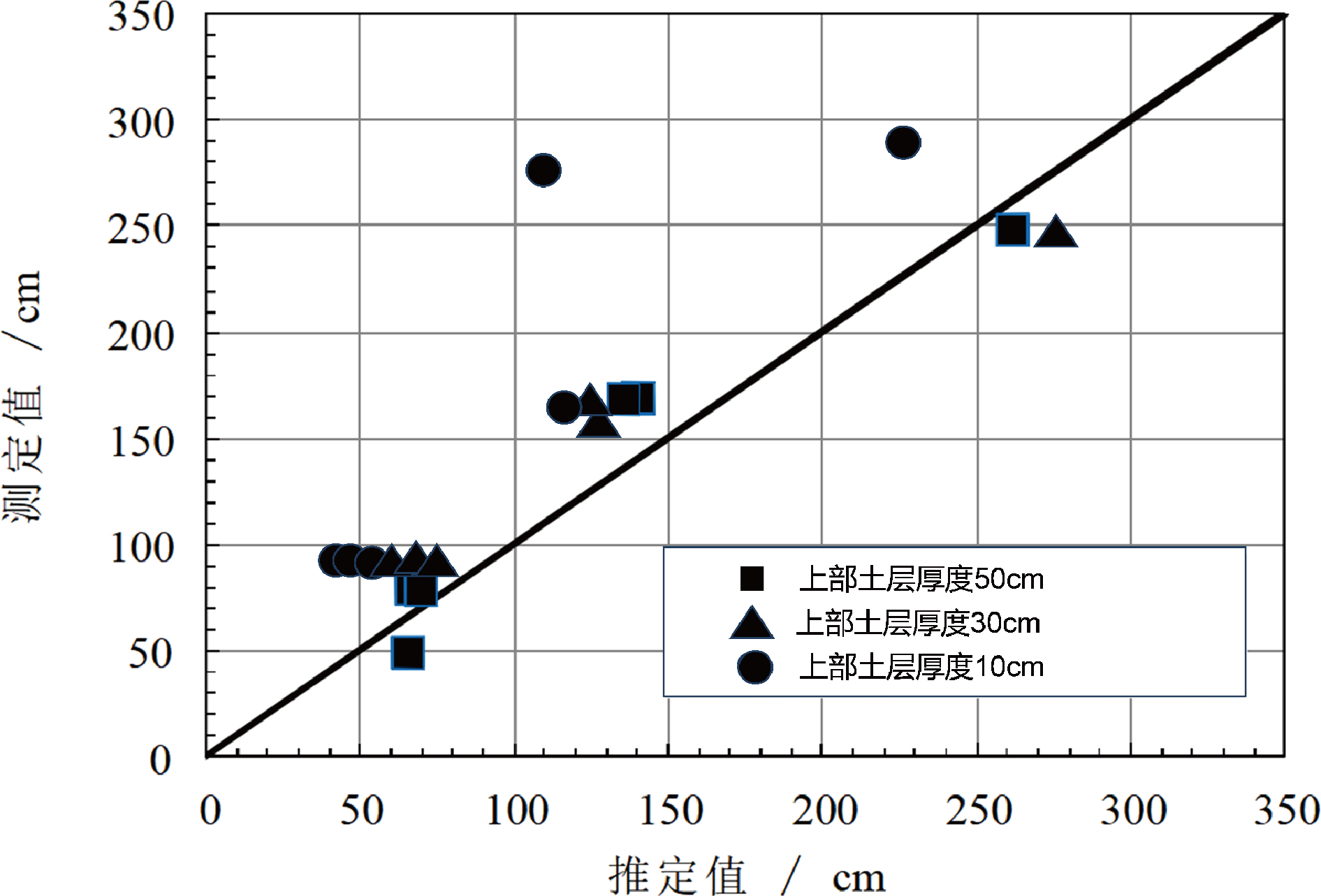
图9 显示了 50 cm、30 cm 和 10 cm 厚度的上层土壤极限长度预测值和测量值的比较结果。50 cm 厚的上层土壤(细砂)的结果,测量值和预测值之间有很好的一致性,这表明此条件是可以应用极限长度估算公式的。厚度为30 cm的上层土壤的试验结果,当极限长度较长时,测量值趋于缩短。厚度为 10 cm 的上层土壤的试验结果,但测量结果有很大差异。在上层土层 30 cm 厚和上层土层 10 cm 厚的情况下,土层厚度小于空气渗透值,应用经典公式时认为土层厚度为 ha。当上层土层 10 cm 厚,层厚极小于空气渗透值,被认为不在极限长度估算公式的适用范围内。然而,在8号硅砂的情况下,当层厚超过30 cm时,可以得到一个稳定的极限长度,并且可以应用极限长度预测公式。
-
图9 极限长度比较
-
在本试验中,通过测量没有从上层土壤渗入中层土壤的流量来评估进入中层土壤的渗透通量。表6显示了渗透率为80%时的平均值计算极限长度的结果。这两个值平均相差 4% 左右,对估计极限长度的影响很小,所以可以用这个值作为渗透率提前估计极限长度。
-
从上层突破并渗入中层的水可能在断裂点处具有局部高流速,呈指状流动。在这种情况下,中间层的水流与降雨的均匀通量分布不同,经典公式可能不适用。但是,由于从极限长度方程得到的长度与试验结果基本一致,即使在某些区域出现大的局部流动,在本试验中,中心砂层厚 50 cm,流动会在向下渗透的过程中被平均化,因此认为应用经典公式可适用。
-
4 结论
-
本文在两层CB地层和具有覆土结构的三层CB 地层上进行了大规模的土槽试验,明确了应用极限长度估算公式时所需的覆土层厚度。主要结论如下:
-
(1)当经典计算用于细砂为上层土的两层 CB 工况,上层土的厚度应在50 cm左右,且至少要有一个空气渗透值的厚度,低于 30 cm 的厚度往往造成计算值的高估。
-
(2)当经典计算用于具有覆土结构的三层 CB 地层,以微细砂为上层土,上层土的适用厚度应在 30~50 cm。
-
(3)对三层 CB 地的中、下层土层的工况应用经典计算方程,在上部土层(微细砂层)和中部土层 (细砂层)的情况下,80% 的渗透率对于结果适用性最佳。
-
参考文献
-
Froude J M, Petley N D. 2018. Global fatal landslide occurrence from 2004 to 2016[J]. Natural Hazards and Earth System ciences, 18 (8): 2161-2181.
-
Genuchten V, Th M. 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 44(5): 892-898.
-
Jian G Y, Xiong H Z, Gu P L. 2013. Study of water penetration length and processing parameters optimization in water-assisted injection molding[J]. International Journal of Advanced Manufacturing Technology, 69(9/12): 2605-2612.
-
Kobayashi K, Suzuki A, Matsumoto K, Morii T. 2019. Study on an appropriate fine soil(sand) for maximizing diversion length for capillary barrier of soil[J]. Japanese Geotechnical Journal, 14 (1): 43-46.
-
Kung K. 1990. Preferential flow in a sandy vadose zone: 2. Mechanism and implications[J]. Geoderma, 46(1/3): 59-71.
-
Miyazak T. 1995. The diversion capacity of an inclined capillary barrier [J]. Transactions of the Agricultural Engineering Society Japan, 63: 49-56.
-
Ross B. 1991. Reply [to "Comment on 'The Diversion Capacity of Capillary Barriers' by Benjamin Ross"][J]. Water Resources Research, 27(8): 2157-2157.
-
Steenhuis T S, Parlange J Y, Kung K. 1991. Comment on ‘The Diversion Capacity of Capillary Barriers’ by Benjamin Ross[J]. Water Resources Research, 27(8): 2155-2156.
-
Stormont J C. 1996. The effectiveness of two capillary barriers on a 10% slope[J]. Geotechnical & Geological Engineering, 14(4): 243-267.
-
Tojo Y, Tanaka N, Matsuto T, Matsuo T. 2010. An application of capillary barrier as a leachate drainage system at bottom of landfill. numerical analysis[J]. Proceedings of the Japan Society of Civil Engineers, 692: 53-62.
-
Walter M T, Kim J S, Steenhuis T S, Parlange J Y, Heilig A, Brad⁃dock R D. 2000. Funneled flow mechanisms in a sloping layered soil: Laboratory investigation[J]. Water Resources Research, 36 (4): 841-849.
-
Yang F, Fan X, Subramanian S S, Dou X Y, Xu Q. 2021. Catastrophic debris flows triggered by the 20 August 2019 rainfall, a decade since the Wenchuan earthquake, China[J]. Landslides, 18(9): 1-16.
-
Zhan T L T, He L, Jia G W, Chen Y M, Fredlund D G. 2014. Physical and numerical study of lateral diversion by three-layer inclined capillary barrier covers under humid climatic conditions[J]. Canadian Geotechnical Journal, 51(12): 1438-1448.
-
陈冠一, 肖杰, 陈强, 杨和平, 常锦, 邹维列, 陈汪洋 . 2022. 不同毛细阻滞覆盖层处治膨胀土边坡的渗流及稳定性研究[J]. 中南大学学报(自然科学版), 53(1): 199-213.
-
黄涛, 罗喜元, 邬强, 郑黎明 . 2004. 地表水入渗环境下边坡稳定性的模型试验研究[J]. 岩石力学与工程学报: 23(16): 2671- 2675.
-
刘利嘉, 何明辉, 余荣坤 . 2021. 四川都江堰白依庵泥岩矿高陡边坡环境治理和生态修复[J]. 矿产勘查, 12(2): 489-496.
-
刘秋强, 胡嫚, 吕杰堂, 程凯 . 2021. 地下水渗流作用下的三峡库区巴东县赵树岭滑坡稳定性研究[J]. 矿产勘查, 12(7): 1647-1654.
-
王家琛, 朱鸿鹄, 王静, 曹鼎峰, 苏立君, Narala Gangadhara Reddy. 2021. 基于主动加热光纤法的毛细阻滞入渗模型试验研究[J]. 岩土工程学报, 43(1): 147-155.
-
闫新亮, 王新建, 王继峰 . 2019. 贵西某高陡岩质边坡生态恢复治理实践[J]. 矿产勘查, 10(11): 2865-2869.
-
摘要
毛细屏障(CB)导流长度是评估边坡加固效果的关键。先前对于导流长度的推导以二层覆土结构为基础,而地质调查工程中发现,上部土层厚度影响显著,计算缺乏适用性评估。本次研究在二层结构试验基础上改变上部土层厚度,并针对三层覆土结构的降雨入渗进行分析,阐明了二、三层 CB导流长度近似方程的应用。研究结果表明:(1)二层结构中,与经典分析不一样的是,当上部土层厚度小于30 cm时,试验导流长度极限值小于计算值,而上部为微细砂时,计算值至少需要考虑一个空气渗透值的厚度;(2)三层CB 结构试验中,含有细砂上部适用厚度为 30~50 cm,80%的渗透率对于解析解的适用性最佳。一系列大型土槽试验具体指出极限长度预测公式的适用范围,大大提高了计算结果的适用性及准确性,可为边坡加固的评估提供更精准的预测。
Abstract
The capillary barrier (CB) diversion length is critical in assessing the effectiveness of slope stabilization. The previous derivation of the diversion length was based on a two-layer overburden structure. While researchers found that the thickness of the upper soil layer has a significant effect on the stability, and the calculation lacks applicability assessment during the geological investigation. In this study, the application of the approximate equations for the length of CB diversion length in the two-layer and three-layer is clarified by varying the thickness of the upper soil layer on the basis of the test of the two-layer structure and analyzing the rainfall infiltration for the three-layer overburden structure. The results of the study show that (1) in the two-layer structure, unlike in the classical analysis, the limit value of the experimental infiltration length is smaller than the calculated value when the thickness of the upper soil layer is less than 30 cm, whereas the calculated value needs to take into account at least one air infiltration value of the thickness of the upper part, when the upper part is a microfine sand;(2) In the test of three-layer CB structure, the applicable thickness of the upper part containing fine sand is 30-50 cm, and 80% permeability is the best applicable for resolved solution. In this study, a series of large-scale soil trench tests specifically point out the scope of application of the limit length prediction formula, which greatly improves the applicability and accuracy of the calculation results, and can provide more accurate predictions for the assessment of slope stabilization.
Keywords
geological survey engineering ; capillary barrier ; inflow length ; model test