-
0 引言
-
在中国地下开采的矿山中,无底柱分段崩落法占有相对较大的比重,它是一种结构简单、安全高效的采矿方法。在采场大结构参数的市场驱动下,极大地提高了采矿效率、降低了采矿成本(范庆霞和李祥凤,2016)。由于无底柱分段崩落法在空间分布上具有特殊的结构,因此近年来很多学者对无底柱分段崩落法采场的稳定性进行了研究。例如,李志鹏等(2011)发现采场的应力分布与回采顺序有关,合理的回采方案可以明显地改善矿体的应力状态,而且可以提高矿石的回收率;苗胜军等 (2016)通过数值模拟的方法对大间距无底柱分段崩落法左往右的开采顺序下采场的稳定性影响进行了研究;张昌太(2004)发现某矿山采用无底柱分段崩落法在采用了先东西后中央的不合理回采顺序的条件下,加剧了中部地段的应力集中程度,造成了局部地段的地压显现程度明显高于其他地段。郭辉文等(2020)采用FLAC3D数值模拟软件针对充填体下无底柱分段崩落法采场的不同结构参数对回采进路的稳定性进行了研究,研究结果表明无底柱分段崩落法采场的不同结构参数对采场的稳定性存在不同程度的影响,且研究发现进路两帮的安全性优于进路顶底板。王伟等(2020)通过FLAC3D 的数值模拟手段对陈四楼煤矿井下深部围岩的应力进行了分析,并对支护体的位移进行了研究,研究结果为矿山的安全生产奠定了科学基础。李川和张明(2018)通过FLAC3D的数值模拟方法对某矿山井下巷道围岩的应力、位移及塑性区进行了大量的研究。虽然无底柱分段崩落法具有上述的很多优点,但是在回采顺序、爆破和出矿管理等方面需要进行严格的把控,这样才能保证无底柱分段崩落法高效、安全的生产。本文就无底柱分段崩落法不同回采顺序对采场稳定性的影响进行研究。
-
1 研究方案
-
此次研究针对采用无底柱分段崩落法开采的矿山比较常见的 3 种回采顺序进行采场稳定性分析,采场结构参数设计为:H × B × L = 15 m × 15 m × 2.5 m,即分段高度为 15 m,进路间距 15 m,崩矿步距为 2.5 m(即为排距 L)。进路规格为 a × b = 4.8 m × 4.4 m(宽×高)直墙半圆拱,并设置 3 个分段,模拟中假设模型的埋深为200 m,测压系数为1。以首采分段为研究对象,分析无底柱分段崩落法回采过程中不同回采顺序对下部采场稳定性的影响,其 3种回采顺序的平面示意图如图1所示。此次研究的内容主要有两个,一是分析这 3 种不同回采顺序各自回采过程中采场的应力分布特点;二是分析这 3 种回采顺序当回采至相同体积矿石时,采场的受力状态的差异,并优选出哪种回采顺序条件下采场的受力最均匀、稳定性最好。
-
2 模型的建立
-
模型总体上分为2部分,上部为覆岩,下部为矿体。由于开挖巷道为直墙半圆拱形且半径为 2.4 m,因此为便于从力学角度进行分析,将巷道的围岩受力情况简化为圆形巷道进行研究,其平衡方程为,几何方程为,将边界条件 r = a,σr = 0;r → ∞,σθ → p 带入平衡方程和几何方程后得切向应力 σθ 与径向应力 σr 的解析表达式为:
-
图1 不同回采顺序平面示意图
-
a—各进路同时回采;b—呈“凸”字形阶梯状回采;c—呈阶梯状回采
-
式(1)中,a 表示巷道的半径,单位为 m;p 表示原岩应力,单位为 MPa;r表示以巷道中点为圆心巷道周边的受力范围,单位为m。
-
从工程观点考虑,应力变化不超过 5% 便可以忽略其影响,根据式(1)计算得到,当 r = 5a时,σθ ≈ 1. 04p,与原岩应力相差小于5%,故模型建立的围岩边界长度为矿体开挖半径长度的5倍即7.5m × 5 = 37.5m,除此以外模型中为保证模拟的准确性,覆岩的厚度建为30 m,矿体高度为56 m。因此模型的大小为长×宽×高=150 m×200 m×86 m。共建立 71436 个节点,67620个单元,其模型如图2所示。
-
2.1 力学参数的选取
-
模型中上部覆岩及下部矿体的力学参数参照某矿山矿石及覆岩力学指标,该矿山各岩层的岩石力学参数如表1所示。由于岩石的物理力学性质与弹塑性材料性质相似,且岩体的破坏形式主要是剪切和拉伸。因此,模型采用摩尔-库伦本构模型(吉彪,2018;王振军和邱晔,2018),开挖部分采用空单元(null)模型(黄敏等,2017)。由于 FLAC3D 中摩尔-库伦本构方程所涉及到的参数分别为:体积模量K、剪切模量G、内摩擦角fric、粘聚力coh和抗拉强度 tens。因此需要将表1 中各岩层的部分岩石力学参数根据公式(2~5)做相应的转化,可得出各岩层岩体单轴抗拉强度σmc、体积模量K和切变模量G。
-
图2 模型示意图
-
式(2~4)中,E 为弹性模量,单位为 GPa;v 为泊松比;c 为内聚力,单位为 MPa;ϕ 为内摩擦角,单位为°。
-
由于该矿山所提供的力学参数为岩石力学参数,而 FLAC3D 数值模型中所要用到的参数为岩体的力学参数,因此需要根据Hoek-Brown岩体强度折减公式(展国伟等,2007;翁敬良,2010)对其进行折减,Hoek-Brown岩体单轴抗拉强度折减公式为:
-
式(5)中,σmc 为岩体单轴抗拉强度,σc 为单轴抗压强度,m、s参照《非煤露天矿边坡工程技术规范 (GB 51016-2014)》(中华人民共和国住房和城乡建设部,2014)选取。
-
2.2 边界条件
-
边界条件分为真实边界和人为边界两类。真实边界存在于模型中的真实物理对象,而人为边界是为了封闭单元体所做的人为假定。控制模型边界的物理量主要有 2 个,分别为指定位移和指定应力。Apply 命令对模型网格内外边界、内部节点和单元体施加力学边界条件;Fix命令对模型中节点的速率、位移固定不变。鉴于此次模拟采用的是摩尔-库伦本构模型,因此模拟中假设模型为各向同性的均质体且不考虑节理裂隙、时间效应和地下水的渗流影响。
-
3 模拟结果及数据分析
-
FLACD3D数值计算结果中,最大主应力是以数值来计算的,忽略了应力的方向。因此计算结果中,实际最大主应力应为负方向应力。
-
当无底柱分段崩落法采用以上3种不同回采顺序回采相同体积的矿石时(此次模拟各回采顺序均回采3000 m3 矿石),采场中的最大主应力分布图(矿体顶部剖面图)如图3、图4及图5所示,各分段巷道顶板的最大垂直位移如图6、图7和图8所示。
-
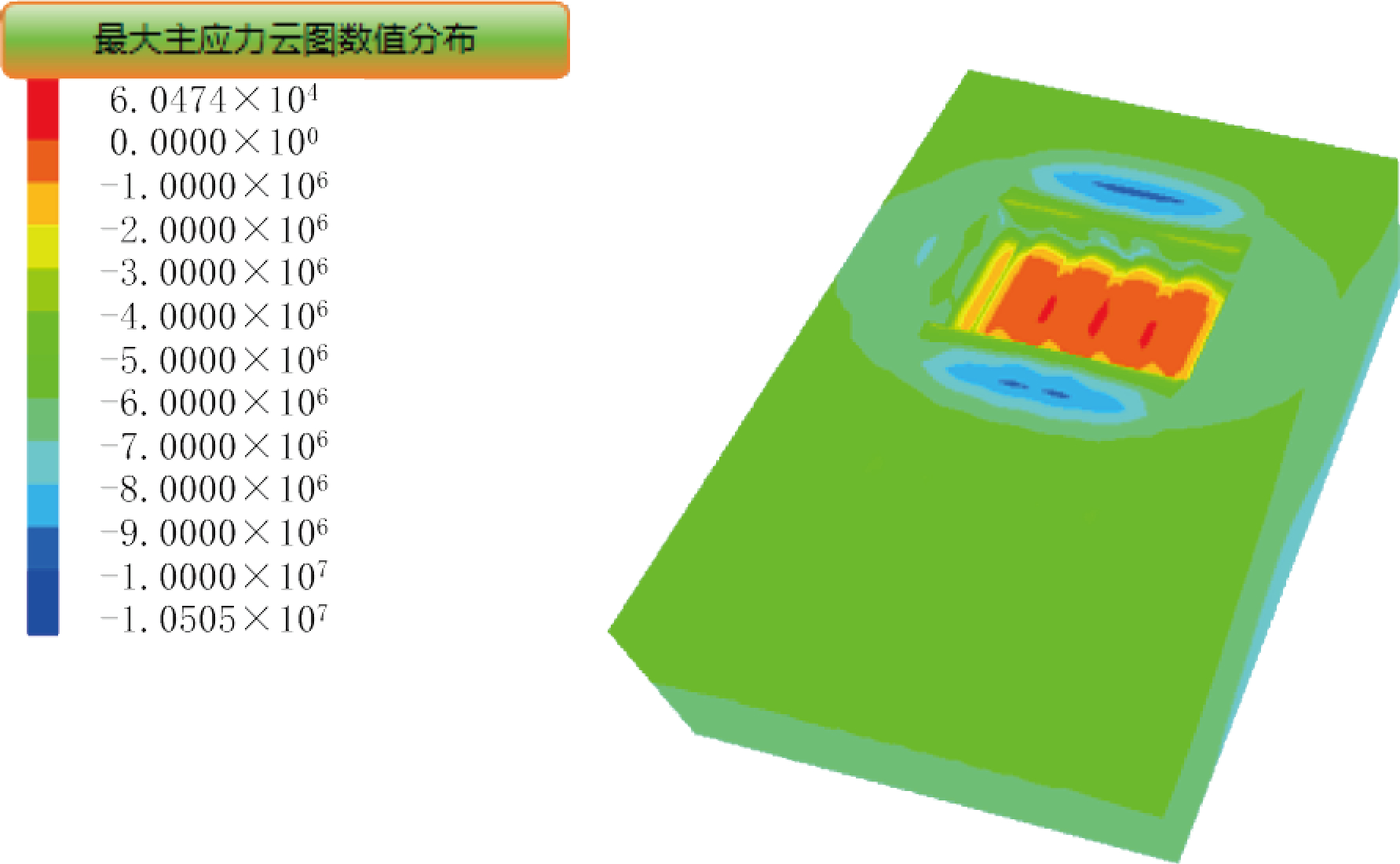
图3 各进路同时回采最大主应力分布图
-
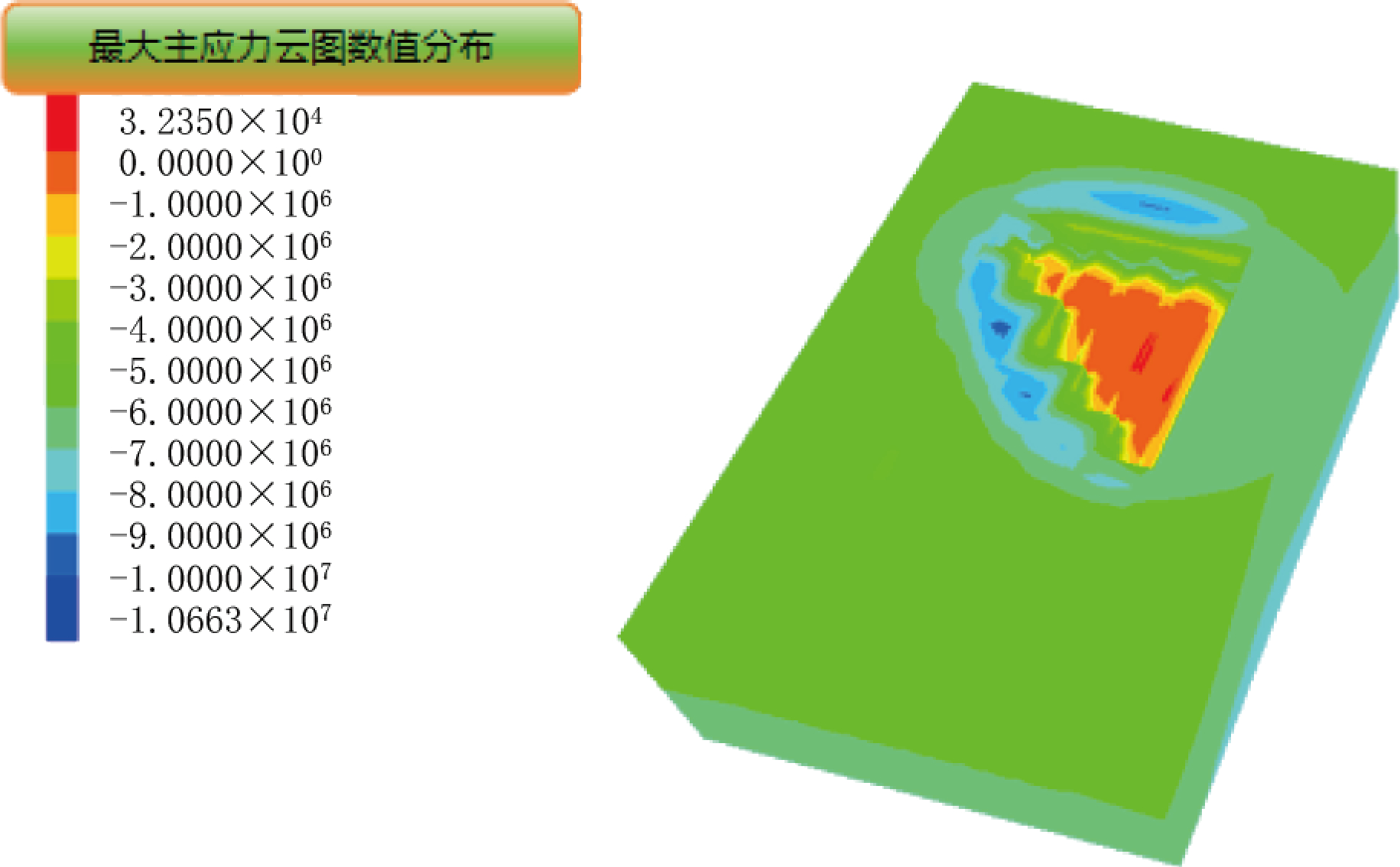
由图可知(图3、图4 及图5),无底柱分段崩落法开采中无论采用何种回采顺序只要矿体开采后,进路顶部矿体应力重新分布的结果均为剪应力占主导地位。当开采相同体积的矿石时,回采顺序 1 (各进路同时回采):采场中的最大主应力主要分布在上下盘位置,分布均匀且最大主应力约为 10.51 MPa;回采顺序 2:(各进路呈“凸”字形阶梯状回采) 采场中的最大主应力主要集中在“凸”字形阶梯附近,部分集中在上盘,且最大主应力约为 10.77 MPa;回采顺序 3:(各进路呈阶梯状回采)采场中最大主应力沿阶梯分布且分布不均匀,其中2#和3#进路顶部矿体受力最大,5#进路上部矿体受力最小。这是因为在进路 1#~5#方向上开采的矿石越来越多,空区越来越大,应力逐渐向空区周围叠加,而2# 和 3#进路开采矿石较少,空区面积较小,未开采矿体居多,4#~5#形成的空区所造成的应力叠加在 2# 和 3#矿体上部,属于应力集中区,且最大主应力约为10.66 MPa。根据以上模拟结果可以看出各进路呈“凸”字形阶梯状回采时,采场中应力叠加的值最大,各进路同时回采时,采场中应力叠加的值最小。
-
图4 各进路呈“凸”字形阶梯状回采最大主应力分布图
-
图5 各进路呈阶梯状回采最大主应力分布图
-
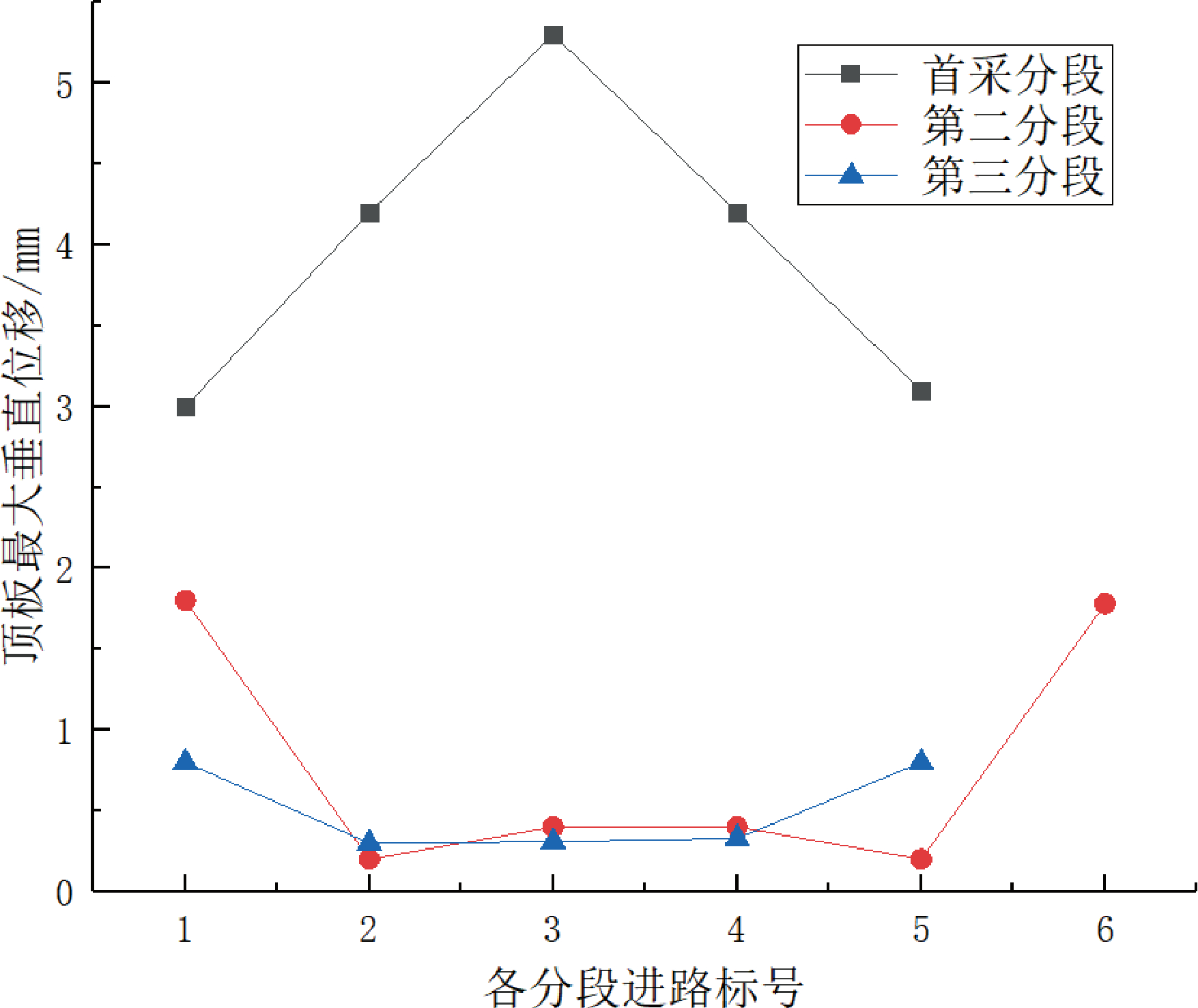
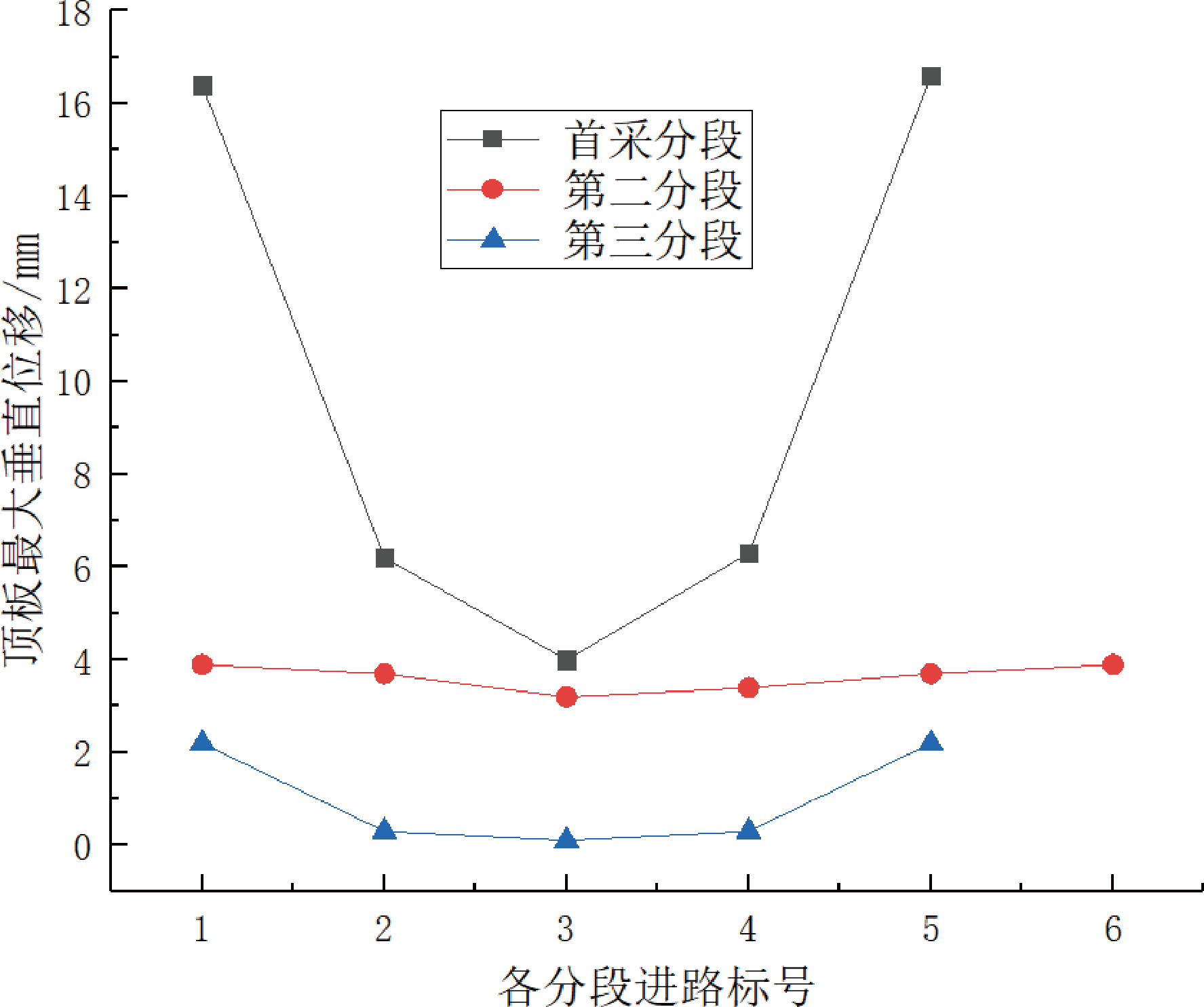
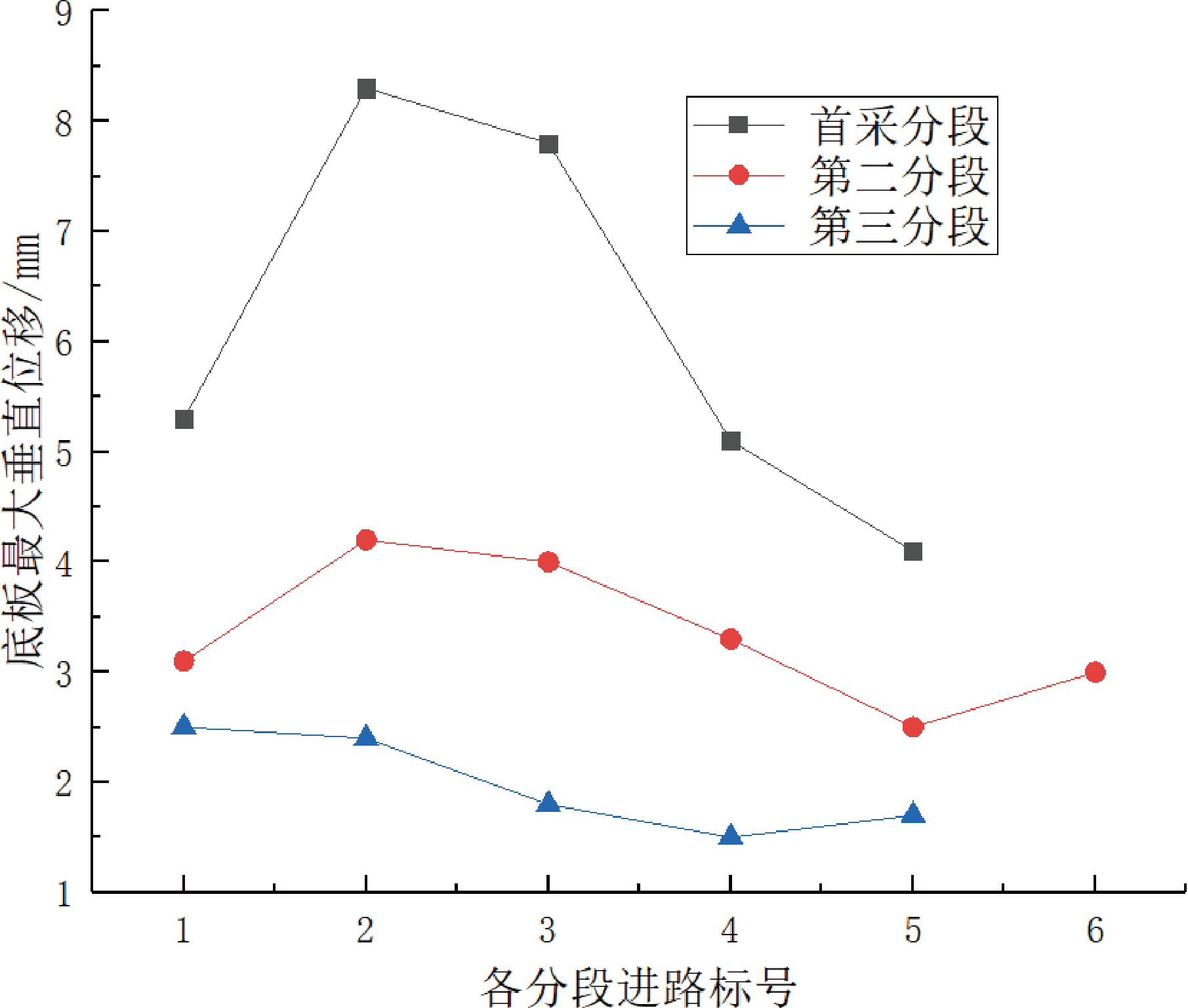
由图可知(图6、图7 及图8),无底柱分段崩落法采用上述 3 种方法回采时,首采分段进路受垂直应力的影响产生的垂直方向的位移变化最为明显,第二、三分段进路中垂直位移变化各有不同。
-
图6 各进路同时回采巷道顶板最大垂直位移分布图
-
图7 各进路呈“凸”字形阶梯状回采巷道顶板最大垂直位移分布图
-
图8 各进路呈阶梯状回采巷道顶板最大垂直位移分布图
-
其中当采用各进路同时回采的方案时,首采分段中间进路产生的位移最大,两边产生的位移相对较小,第二和第三分段位于最外侧进路中垂直位移相对较大,中间进路垂直位移变化不大,这是因为随着崩落的进行,上覆岩层的垂直压力逐渐向周围转移并向矿体中部聚集的结果。
-
当呈“凸”字形阶梯状回采时,应力会向采场中未开采矿体集中,导致进路中垂直方向的位移呈现周边位移大,中间位移小的趋势,并且第二和第三分段也呈现这种相同的趋势;当各进路呈阶梯状回采时,垂直方向上位移变化大的进路主要集中在2# 和3#进路,且第二和第三分段进路中垂直位移变化区域与首采分段相同。通过上述应力分析可知,2# 和 3#进路上部矿体是承受压力最大的位置。因此此处位移分析与上述应力分析的结果可相互印证。
-
为更科学地研究出不同回采顺序对无底柱分段崩落法采场稳定性的影响,需采用系统评价的方法将模拟得到的数据进行综合分析,本次研究采用 AHP权重分析法。
-
4 不同回采顺序的权重优选分析
-
为更科学的研究出不同回采顺序对无底柱分段崩落法采场稳定性的影响,需采用系统评价的方法将模拟得到的数据进行综合分析,本次研究采用 AHP权重分析法。
-
4.1 AHP模型的构建
-
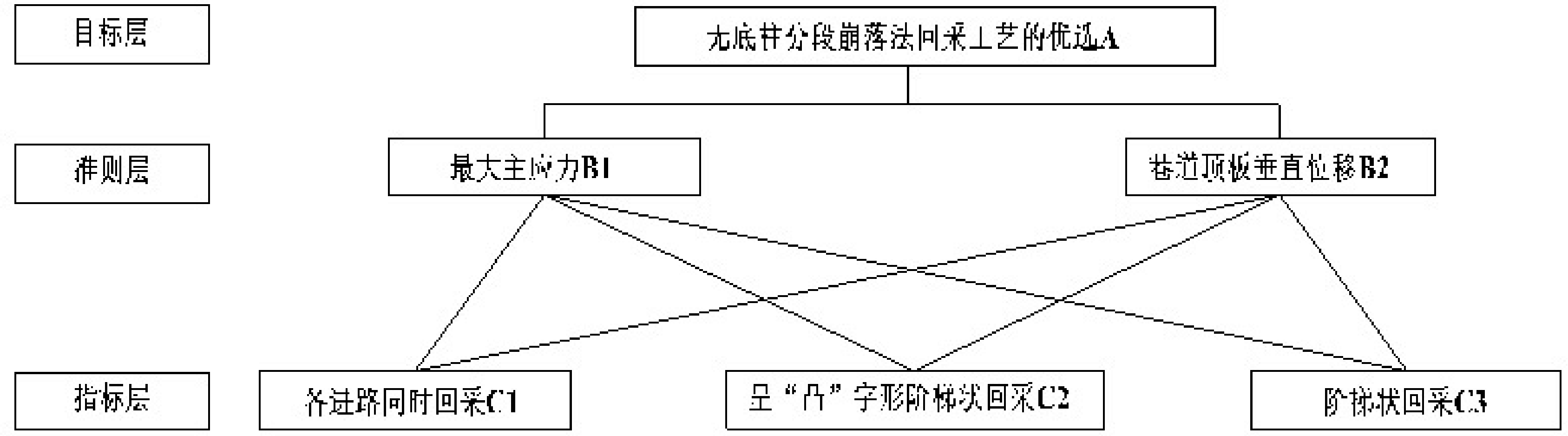
结合图1并根据上述无底柱分段崩落法 3种不同的回采顺序的模拟结果,将模拟参数进行分层构建并建立AHP模型,如图9所示。
-
4.2 各回采顺序的权重分析
-
将首采分段、第二分段及第三分段的模拟数据汇总,分别如表2、表3和表4所示。
-
结合表2~表4,构造判断矩阵,分别如下所示:
-
(1)首采分段判断矩阵
-
图9 无底柱分段崩落法回采工艺的评价指标层次结构
-
(2)第二分段
-
(3)第三分段
-
将上述判断矩阵进行权重计算得到各判断矩阵的特征向量及相应参数,具体如表5所示。
-
注:C. I. 表示一次性检验指标;R. I. 表示随机一次性指标,用于对C. I. 的校正;C. R. 为判断矩阵一次性检验准则指标。
-
将不同分段的巷道顶板及不同回采顺序条件下的最大主应力的各权重进行综合分析,并经过计算分别得到不同回采顺序条件不同分段的优选级。
-
即首采分段
-
同理可得,第二分段和第三分段的优选级分别为:(0.2737,0.3751,0.3512)T、(0.3214,0.3352, 0.3434)T。
-
由于无底柱分段崩落法具有的特殊性,首采分段开采顶板要优先冒落,尽快形成覆盖层,以确保后续的安全开采,因此首采分段需依据判断矩阵最大隶属度原则,可以得出,回采过程中“凸”字形阶梯状回采对采场的安全生产具有较大的作用;第二及第三分段开采,由于覆盖层已经形成,因此需要维护采场的稳定性,而第二和第三分段的判断矩阵是根据采场的严重程度进行构造的,因此第二和第三分段应依据最小隶属度原则对采场的安全生产做出判断,所以经计算得出,各进路同时回采时,更利于维护无底柱分段法采场的稳定。
-
5 结论
-
通过上述 3 种不同的回采顺序可以得知,当采用“凸”字形阶梯状回采时,无论是首采分段还是第二、三分段巷道产生的垂直位移均是最大的,并且矿体受来自垂直方向的力也是最大的;当各进路同时开采时,采场中受的力最小,各进路顶板的垂直位移也最小,采场最为稳定,但是各进路同时回采在首采分段产生的空区形态为矩形,且连续、完整,当上覆岩层冒落时会形成巨大的冲击地压不利于采场的安全;当各进路呈阶梯状开采时,采场受到的力和各进路顶板垂直方向的位移均介于上述两种回采顺序之间。结合对不同回采顺序的权重分析可以得出,“凸”字形阶梯状回采时,采场的应力最大,各进路同时回采时应力最小。
-
由此可见,为尽快形成覆盖层,首采分段应采用“凸”字形阶段状回采顺序;其他分段为最大程度保证采场的稳定性,需采用各进路同时回采的顺序对矿体进行开采。
-
参考文献
-
东启亮, 张路飞, 张志科, 李谦谦, 王梦然 . 2020. 基于 AHP 的大尺度空间域矿山地质环境评价研究[J]. 矿产勘查, 11(8): 1780‒1787.
-
范庆霞, 李祥凤. 2016. 无底柱分段崩落法过联络巷道回采工艺的探讨[J]. 化工矿物与加工, 45(3): 52‒54.
-
郭辉文, 何治良, 张志贵, 苏华友, 朱强. 2020. 充填体下无底柱分段崩落法采场结构参数对回采进路稳定性影响分析[J]. 矿业研究与开发, 40(4): 12‒18.
-
黄敏, 唐绍辉, 黄英华, 吴亚斌. 2017. 基于ANSYS-FLAC3D的采空区稳定性分析数值模拟研究[J]. 矿业研究与开发, 37(6): 78 ‒83.
-
吉彪. 2018. 矿井采空区地表塌陷的机理分析[J]. 山西能源学院学报, 31(5): 1‒3, 6.
-
李川, 张明. 2018. 深井上下山煤柱区巷道围岩响应特征数值模拟及其灾害控制[J]. 矿产勘查, 9(11): 2246‒2249.
-
李志鹏, 杨闯, 王宝文, 叶会师 . 2011. 回采顺序调整和结构优化在司家营铁矿Ⅲ采场的应用[C]//中国金属学会 . 第十八届川鲁冀晋琼粤辽七省矿业学术交流会论文集 . 河北钢铁集团滦县司家营铁矿有限公司, 3.
-
苗胜军, 史丽超, 白玉冰, 王浩 . 2016. 大间距无底柱分段崩落法开采稳定性分析[J]. 矿冶, 25(2): 1‒4.
-
王伟, 李小龙, 宋彦琦, 李向上, 马宏发. 2020. 基于FLAC3D的巷道分步开挖支护稳定性模拟研究[J]. 矿产勘查, 11(9): 2045‒ 2052.
-
王振军, 邱晔 . 2018. 基于 FLAC3D 数值模拟的钻孔变形特征及围岩稳定性研究[J]. 能源与环保, 40(12): 21‒24.
-
翁敬良 . 2010. 基于改进广义 Hoek-Brown 准则岩质边坡稳定性分析强度折减法[D]. 长沙: 湖南大学.
-
展国伟, 夏玉成, 杜荣军. 2007. Hoek-Brown强度准则在FLAC3D数值模拟中的应用[J]. 采矿与安全工程学报, 24(3): 366‒369.
-
张昌太. 2004. 桃冲铁矿无底柱分段崩落法采矿的地压问题与控制方法[D]. 青岛: 中国海洋大学.
-
中华人民共和国住房和城乡建设部. 2014. 非煤露天矿边坡工程技术规范(GB 51016-2014)[S]. 北京: 中国计划出版社.
-
摘要
无底柱分段崩落法是金属矿山地下开采中最重要的采矿方法之一,与其他采矿方法相比在空间上具有特殊的结构形式。在实际生产中,由于其所具备的空间结构特殊性,导致其以不同的回采顺序开采矿石时对采场的稳定性影响很大。同时在矿石回采过程中,采场极易形成应力集中的现象,不利于采场的稳定。为此,本文采用FLAC3D数值模拟技术对无底柱分段崩落法经常采用的3种不同回采顺序(各回采进路同时回采、呈“凸”字形回采和阶梯状回采)进行数值研究,研究在3种不同回采顺序下,采场围岩的应力及变形特征,而后将模拟结果通过AHP方法构造判断矩阵进行权重分析。通过大量计算最终得出:无底柱分段崩落法首采阶段覆盖层尚未形成时,应采用“凸”字形阶段状回采顺序;其他分段应采用各进路同时回采的顺序对矿体进行开采,以最大的限度维持采场的稳定性。
Abstract
The bottomless pillar segmented caving method is one of the most important mining methods in underground metal mining, and it has a special structural form in space compared to other mining methods. In actual production, due to its unique spatial structure, mining ore in different mining sequences has a significant impact on the stability of the mining site. At the same time, during the process of ore extraction, the mining area is prone to stress concentration, which is not conducive to the stability of the mining area. Therefore, this article uses FLAC3D numerical simulation technology to conduct numerical research on three different mining sequences commonly used in the bottomless pillar segmented collapse method (simultaneous mining of each mining route, convex shaped mining, and stepped mining), studying the stress and deformation characteristics of the surrounding rock in the mining area under three different mining sequences. Then, the simulation results are used to construct a judgment matrix using the AHP method for weight analysis. Through extensive calculations, it is ultimately concluded that when the cover layer has not yet formed during the first mining stage of the pillar less segmented caving method, a "convex" shaped stage mining sequence should be adopted; The mining of the ore body should be carried out in the order of simultaneous mining of each approach in other sections, in order to maintain the stability of the mining area to the greatest extent possible.
关键词
无底柱分段崩落法 ; FLAC3D数值模拟 ; 回采顺序 ; 权重分析 ; 采场稳定性