-
0 引言
-
地质灾害易发性是指某一地区发生地质灾害的概率,是由该地区的基础地质环境条件所决定,也即“某地容易发生地质灾害的可能性”(宋英旭, 2019)。地质灾害易发性分区是基于地质灾害的形成与发展所依赖的地质环境条件,结合对地质灾害现状、调查、预测和评价结果等信息,采用定性与定量评估相结合的方法来确定地区地质灾害的易发性,目的在于阐明区域内地质灾害的分布规律、发展特征以及危害程度。
-
滑坡易发性评价是一个复杂的研究领域,涉及到地质、地形、气候、土壤等多个因素的综合分析。在过去的几十年里,学者们对滑坡的发生机理与影响因素进行了深入研究,并提出了各种评价方法与模型。然而,滑坡易发性评价面临着一些挑战和局限性,例如数据缺乏、模型复杂性以及不确定性等问题。常见的处理方法包括基于滑坡机理的确定性模型,如斜坡稳定模型(康超等,2011)、水文模型 (田利川和姜建梅,2008)等;非确定性模型包括信息量法(Gao et al.,2006;Wang et al.,2014;王佳佳等,2014;许英姿等,2016)、层次分析法(Yoshimatsu and Abe,2006;许冲等,2009;Pourghasemi et al., 2012;Kayastha et al.,2013;Pourghasemi et al., 2013)、专家系统法(方浩和高姣姣,2012)以及机器学习(马彦彬等,2022)等,机器学习方法主要包括支持向量机(Support Vector Machine,SVM)(Othman and Gloaguen,2014;盛明强等,2021)、人工神经网络 (ANN)(向喜琼和黄润秋,2000;Sevgen et al., 2019)、随机森林(Catani et al.,2013;余坤勇等, 2016;Kim et al.,2017;刘坚等,2018;Dou et al., 2019)和梯度提升决策树模型(GBDT)(Song et al., 2018;陈涛等,2018)等。
-
梯度提升决策树模型(Gradient Boosting Decision Tree,简称GBDT)是一种迭代的机器学习模型,最初由 Friedman 于 2001 年提出(Friedman,2001)。 GBDT 采用梯度提升学习策略,通常称为梯度提升机,由一组函数近似器组成。该模型通过训练多棵决策树(基学习器),按顺序最小化预定义的可微分损失函数,将所有树的预测结果累加以得出最终预测。GBDT在机器学习中被认为是对真实世界分布拟合效果最好的算法之一,尤其适用于处理表格数据样本,具备出色的表征能力。其主要优点包括对连续型和离散型数据的处理能力,输入数据的灵活性,擅长回归分析,包括线性和非线性模式的拟合。由于相对较少的调参时间,该模型预测的准确率也相对较高。在中国,GBDT 模型在滑坡预测方面得到了广泛应用,并其理论已经非常成熟。陈涛等 (2018)以三峡库区秭归—巴东段阳春市,从多源空间数据中提取了9个致灾因子作为区域滑坡易发性分析的评价指标,并基于 Boosting 提升集成学习原理构建了 GBDT 模型。利用经训练的 GBDT 模型对阳春市进行了滑坡易发性分析与评价,并将结果与随机森林模型和信息量模型进行了对比分析。通过受试者工作特征曲线和曲线下的面积对3种模型进行了精度评价,结果显示 GBDT 模型的预测精度为98.9%。宋英旭(2019)使用加权的GBDT模型分析了整个三峡库区的滑坡易发性,获得了比 NASA 公布的全球滑坡易发性分布数据更符合当地实际情况的结果。
-
为确保数据分析的准确性,结合阳春市调查数据的特征与分布,同时考虑了地质灾害点与孕灾地质条件点(主要是阳春市斜坡风险点与削坡建房相关的数据)。以全区地质灾害调查数据为标签,采用机器学习方法进行易发性评价,并构建了孕灾因子样本数据集以评估孕灾因子图层数据特征。在评价过程中,采用了梯度提升决策树模型(GBDT),该模型适用于面向大样本和离散型数据特征的分析(陈涛等,2018)。
-
1 阳春市概况
-
阳春市位于广东省西南部,地理坐标为北纬 21° 50′36″~22° 41′01″,东经 111° 16′27″~112° 09′22″。全市总面积 4037.78 km2,是广东省面积第二大的市(县、区),与恩平市、阳东区、江城区、阳西县、电白区、高州市、信宜市、罗定市、云安区、新兴县相邻,南北长约104 km,东西宽约91 km。
-
阳春市属亚热带季风气候,北回归线以南。气候特征为雨量充沛,热量丰富,冬短夏长,水热光同季。根据气象局提供的资料(2010—2020年),阳春市多年平均气温为 23. 0℃,年平均最高气温为 23.8℃,年平均最低气温为22.3℃。最热的8月份月平均气温为 28.6℃,最冷的 1月份月平均气温为 14.6℃。全年平均无霜期为342 d。
-
阳春市河流主要为漠阳江干流及支流,除春湾镇东部的平河和河㙟镇北部的围底河外,其余为漠阳江的支流。漠阳江干流全长 199 km,集水面积 6091 km2,河床坡降0.494‰。其中在阳春市境内河段长约 165 km,集水面积 4016 km2,河流呈弯曲状态,河面宽度最宽达 300 m。河流水位受降雨季节变化影响,水位变化较大。
-
阳春市地貌形态与构造、地层、岩性等因素相关,成因类型包括构造侵蚀、构造剥蚀、侵蚀溶蚀和侵蚀堆积 4 种。根据形态特征,地貌类型可以细分为中低山、低山、丘陵、低山丛峰林、河谷和平原。阳春市内海拔最高的山峰是位于双滘镇七星村的鸡笼顶,海拔 1280.5 m;最低处位于岗美镇那旦村新阜组,海拔4.5 m,相对高差达1276 m。
-
2 研究方法
-
2.1 数据来源
-
本次研究所使用的数据主要包括以下内容:1∶ 2000地质灾害分辨率精度的数字高程模型(DEM)、地质灾害点(主要包括崩塌和孕灾地质条件点)的地质灾害调查数据以及地区行政区划图、道路交通分布图等多个数据集。
-
其中,DEM地质灾害数据采用地质灾害2. 0 m× 2. 0 m 地质灾害分辨率的栅格数据,用于提取整个阳春市的坡度、坡向、地形起伏度等相关数据。 DEM 地质灾害数据和地质灾害 1:1 万、1:5 万地质灾害调查资料来源于广东省自然资源厅档案馆,用于提取水系信息和区域工程地质岩组信息。地质灾害点的调查数据通过现场实际调查获得。
-
2.2 梯度提升决策树模型(GBDT)
-
GBDT模型的梯度提升算法是梯度下降法的一种近似算法,在GBDT的迭代当中,假设前一步我们获得的强分类器是 Ft-1 ( x),此时的损失函数是 L( y,Ft-1( x))。然后需要寻找一个弱分类器 ht( x)。一方面,该分类器是属于CART回归树模型;另一方面,该分类器能够最小化损失函数:
-
针对第 i 个样本的第 t 轮迭代,其损失函数 (Loss Function)的负梯度可以表示为:
-
用(xi,rti)(i = 1,2,···,m)可以拟合出一棵回归树,其中,第 t 棵回归树的叶子节点是 Rtj,j = 1,2,···,j,这里j是叶节点的数量。
-
对于叶节点的每一个样本,拟合最好的叶节点 ctj可以表示为:
-
所以,可以得到本轮迭代的决策树函数为:
-
对于一个二分类问题,GBDT 的二分类损失函数可以描述为:
-
负梯度误差可以描述为:
-
最终的决策树各叶节点(Leaf Node)de 最优残差拟合值可以表示为:
-
利用 Newton-Raphson 公式,可以将上述公式进一步近似形式为:
-
最终得到的 FM( x)与对数几率 log-odds 相关,可以用来进行概率的计算:
-
本次研究使用全区地质灾害编录数据作为标签,并以各孕灾因子图层数据作为特征构建样本数据集。各因子样本数据集为离散型数据,因子间相互独立,相关系数低,且具有表格型数据特征,适用于 GBDT 模型。因此,本文最终选择梯度提升决策树模型(GBDT)进行易发性评价模型的构建。
-
3 研究内容
-
3.1 评价单元划分
-
地质灾害发育的严重程度受到多个因素影响,在局部区域表现出明显的差异性和复杂性,因此在对阳春市进行风险评价时,评价单元的选取是首要考虑的问题。易发性评价需要对孕灾因子数据进行量化,而评价单元的选取是评价体系建立的基础 (宋英旭,2019)。目前常用的区域地质灾害易发性评价单元有3种类型:规则栅格单元、自然斜坡或地貌单元、行政或地域单元。
-
阳春市地域分布较广,总面积为4037.8 km2,斜坡单元已经不能在全区范围内清晰地表达,同时山区的孕灾地质条件点较多(如削坡建房点),地质灾害体积小,更适合以灾害点形式表示。因此,笔者选择了规则栅格单元作为阳春市地质灾害易发性评价单元。栅格单元具有统一规则的形状和大小,有利于运算和快速划分。鉴于阳春市采用了1∶5万空间比例尺,并根据国家标准《地质灾害风险调查评价技术要求(1∶50000)》的要求,本次评价将栅格大小确定为 25 m×25 m,共划分为 6461921 个栅格单元。
-
3.2 评价指标选取
-
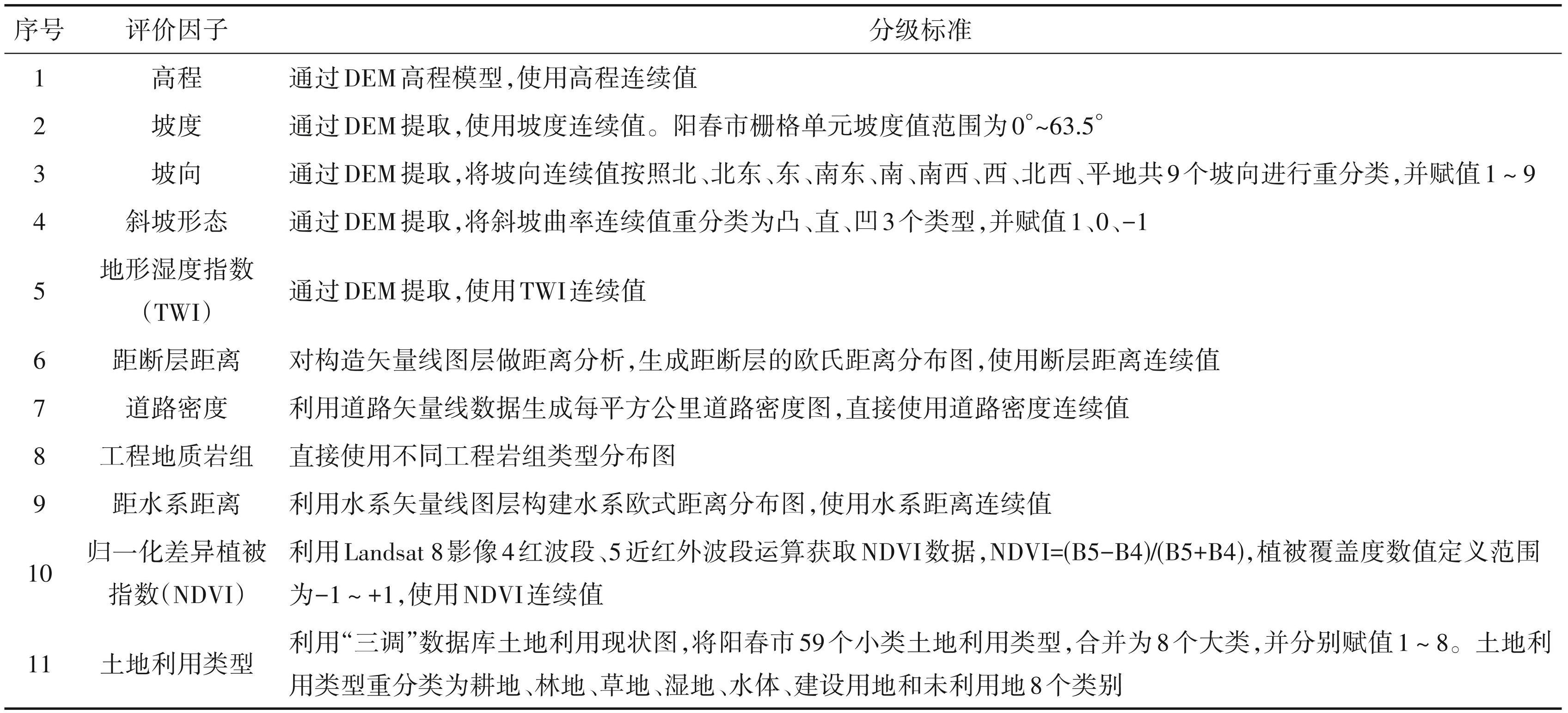
在本研究中,构建的地质灾害易发性评估体系综合选取了高程、坡度、坡向、斜坡形态、地形湿度指数、距断层距离、道路密度、工程地质岩组、距水系距离、植被覆盖度以及土地利用类型这11项关键因子作为评价指标。这一指标体系全面包括了地质、地貌、水文、地表覆盖以及人类活动等多方面因素,为阳春市地质灾害易发性的精准评估提供了一个多维度的分析框架。
-
根据上述各评价因子的数据类型与特征,以及梯度提升决策树模型 GBDT 对样本数据的格式要求,运用GIS空间分析工具对数据进行预处理,提取并制备了高程、坡度、坡向、斜坡形态、地形湿度指数、距断层距离、道路密度、工程地质岩组、距水系距离、植被覆盖度、土地利用类型和地貌分区类型等地质灾害易发性评价因子数据样本。各评价因子的分级信息详见表1,各因子样本数据的空间分布请参见图1~图11。
-
图1 阳春市高程分布图
-
海拔、坡度、坡形都影响着滑坡内部应力的分布,海拔的大小反映的是区域高程的变化情况。高程不仅影响大量的生物、物理参数和人类工程活动,对覆盖层特性也有显著影响,因此采用高程指标来度量高程变化对地质灾害的影响。综合考虑研究区地形地貌和地质灾害分布情况,研究区海拔高程为4.5~1280.5 m,按照经验判断将高程分为5 个类别:<200 m、200~300 m、300~400 m、400~500 m、 >500 m共5类,重分类并赋值1~5。
-
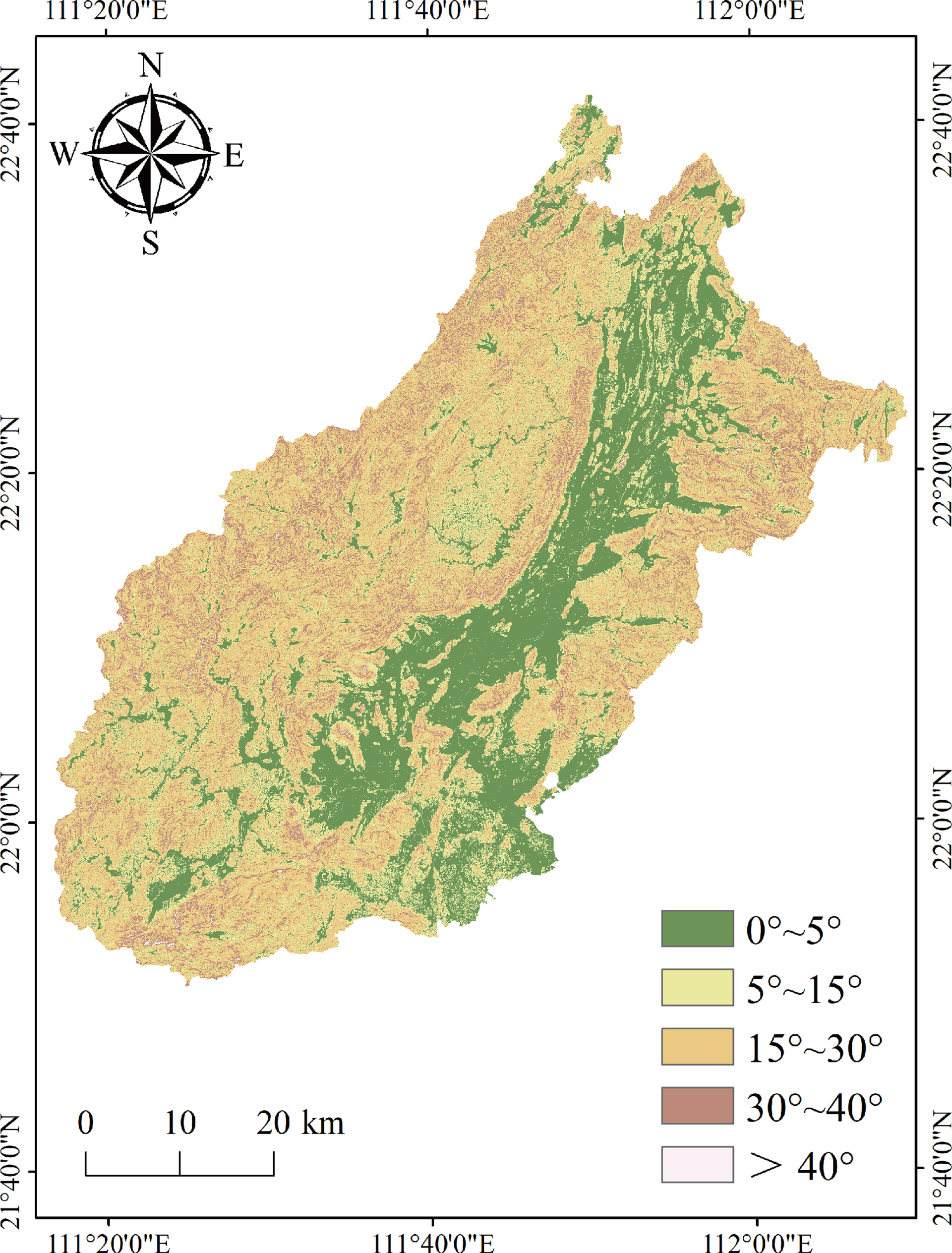
坡度的大小直接影响着斜坡体内应力的分布状态,随着斜坡体坡度的增加,坡底的应力集中且随之增大。坡度对斜坡地下水的补给与排泄、地表水的径流、斜坡上松散物质厚度等都起着控制性的作用,同时坡度也影响着区域水土流失强度以及土地的利用方式等。采用研究区高精度DEM数据,利用 ArcGis表面分析中的坡度分析,生成研究区坡度图。综合考虑研究区地质灾害分布情况,将坡度分级为 5 类,分别为 0°~15°、15°~25°、25°~35°、35°~45°、>45°
-
图2 阳春市坡度分布图
-
坡体接受日照时间的长短和阳光强烈程度受坡向控制。向阳坡(南坡)比背光坡(北坡)的日照、太阳辐射、热量等都要强烈,因此向阳坡温差大、温度高,各种物理化学的风化作用强烈,土层比背光坡更薄,植被覆盖率更低。向阳坡的径流系数较大,冲刷强烈,沟谷深,水土保持较差。基于研究区 DEM数据,利用ArcGIS表面分析中的坡向工具将坡自然斜坡坡向按照顺时针划分为 9 个类别,分别为 337.5°~22.5°(北)、22.5°~67.5°(东北)、67.5°~112.5°(东)、112.5°~157.5°(东南)、157.5°~202.5°(南)、202.5°~247.5°(南西)、247.5°~292.5°(西)、292.5°~337.5°(西北)、-1~0. 001(平面),将上述9个类别重分类并赋值为1~9。
-
滑坡、崩塌等地质灾害可以看作是斜坡体内部应力卸载达到平衡的过程,斜坡体的形状会影响内部应力的发散方向,继而影响地质灾害的发生过程,坡形无法直接计算,而剖面曲率可以表示坡度沿最大坡降方向的地面高程变化率,可以用剖面曲率间接表示斜坡形态。
-
图3 阳春市坡向分布图
-
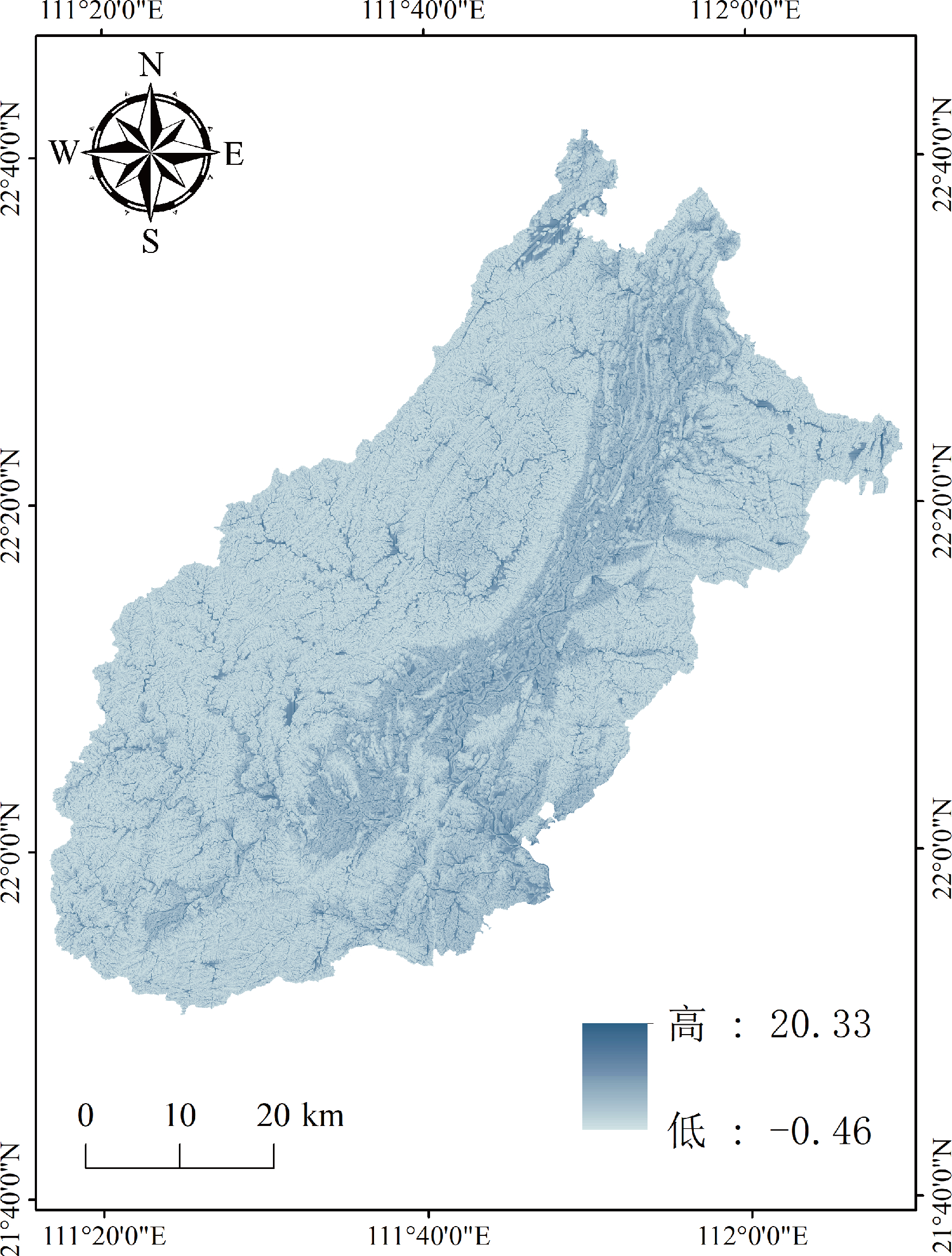
图4 阳春市斜坡形态分布图
-
本次评价选取斜坡剖面曲率<0 表示凹型坡、坡面曲率>0 表示凸型坡、坡面曲率≈0 表示直线或折线型的斜坡体,将斜坡曲率连续值重分类为凸、直、凹3个类型,并赋值1、0、-1。
-
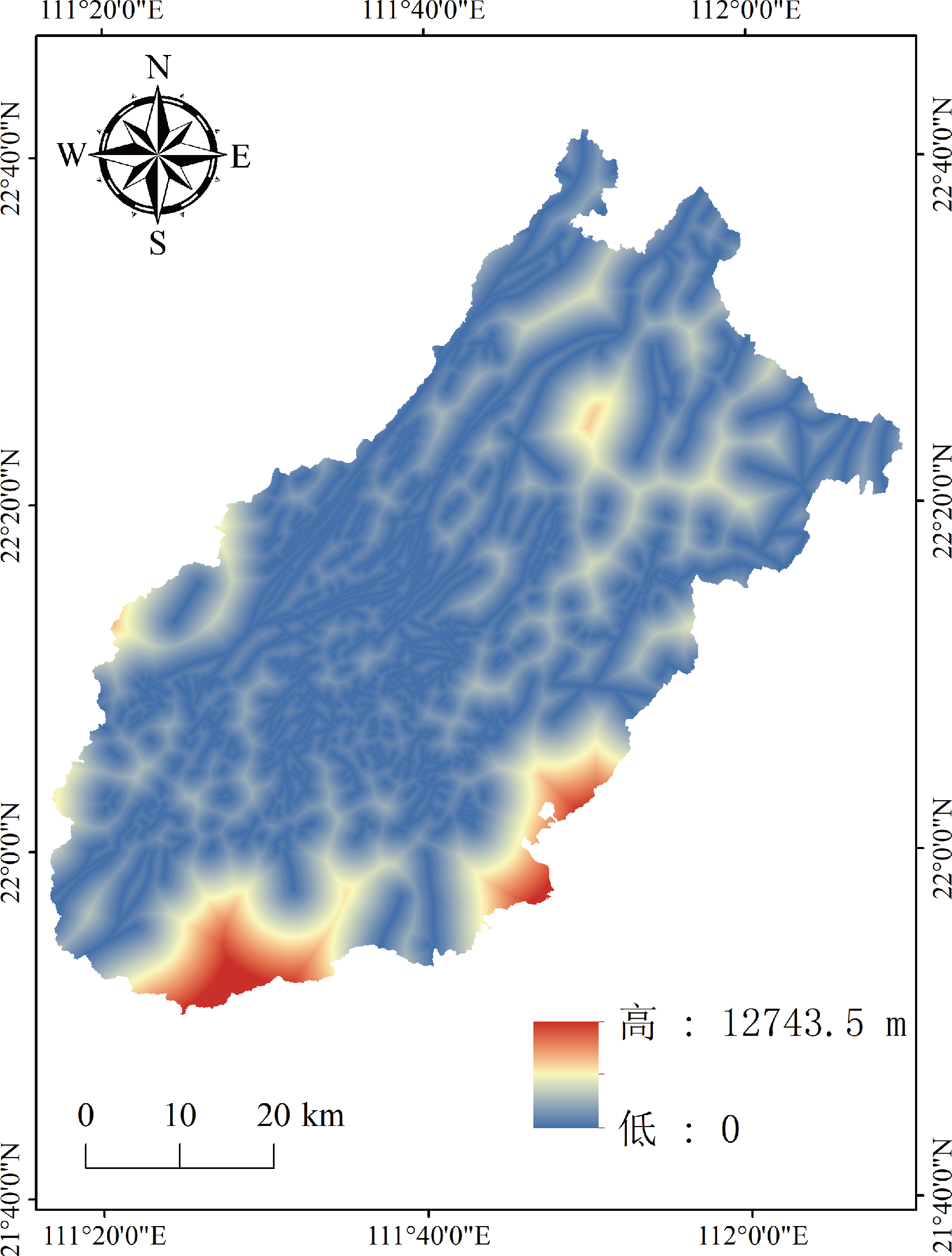
图5 地形湿度指数分布图
-
地形湿度指数(TWI)是区域地形对径流流向和蓄积影响的物理指标。该指数是关于斜坡坡度和上游贡献面积或汇水面积的函数。该指数有助于识别降雨径流模式、潜在土壤含水量增加区域和积水区域。地形湿润度指数,量化了地形对基本水文过程的控制。通过 DEM 提取,计算“单位等高线长度集水面积”或“单位栅格汇流面积”,以表征流域内土壤水份的空间分布。基于 GIS 空间分析,运用地形分析、水文分析等工具完成数据预处理。地形湿度指数(TWI)计算方法在应用于地形平缓地区时会得到不太合理的结果,即在河谷地区,TWI值仅在狭窄的汇水线上数值较高,而在汇水线以外的位置则阶跃式地变为异常低的TWI值。
-
断裂构造对滑坡的影响主要是断层带及其附近一定范围内的岩土体结构遭到破坏,降低了斜坡的完整程度,同时作为重要的地下水通道,对斜坡的变形和破坏带来不利影响。褶皱除引起大范围的岩层产状的变化,而且在褶皱轴迹附近,强烈的构造挤压破坏了岩体的完整性。一般采取对断裂和褶皱轴迹的距离分析来实现,根据断裂或褶皱轴迹的延伸性、规模、类型等地质特征来确定影响范围。为体现断裂构造对研究区地质灾害易发性的影响,本次研究对断裂带两侧延伸范围设置缓冲区,基于GIS空间分析,对构造矢量线图层做距离缓冲分析,生成距断层的欧氏距离分布图。
-
图6 阳春市距断层距离分布图
-
基于GIS空间分析,利用公路、铁路矢量线数据生成每平方公里道路密度图和距道路欧氏距离图。道路密度图通过线密度函数计算获得,为邻域范围内路网长度的连续值。公路矢量图层包括研究区 “三调”数据库中各类道路类型。
-
研究区岩土体按岩石坚硬程度划分为 6 种类型,强度从小到大分别为:松散土层(I)、层状较软变质岩组(Ⅱ)、层状较软红层岩组(Ⅲ)、层状较硬碎屑岩组(Ⅳ)、层状强岩溶化硬碳酸盐类岩组(Ⅴ)、块状较硬—坚硬侵入岩组(Ⅵ),因子数据预处理中将此6类工程地质岩组按1~6进行栅格赋值。
-
基于GIS空间分析,利用研究区水系矢量线、面图层构建水系欧式距离分布图。数据制备过程中对水体数据进行了简化,去除了小面积分布的山塘、养殖坑塘、毛细状人工沟渠,保留了河流、水库和干渠等主要水系。
-
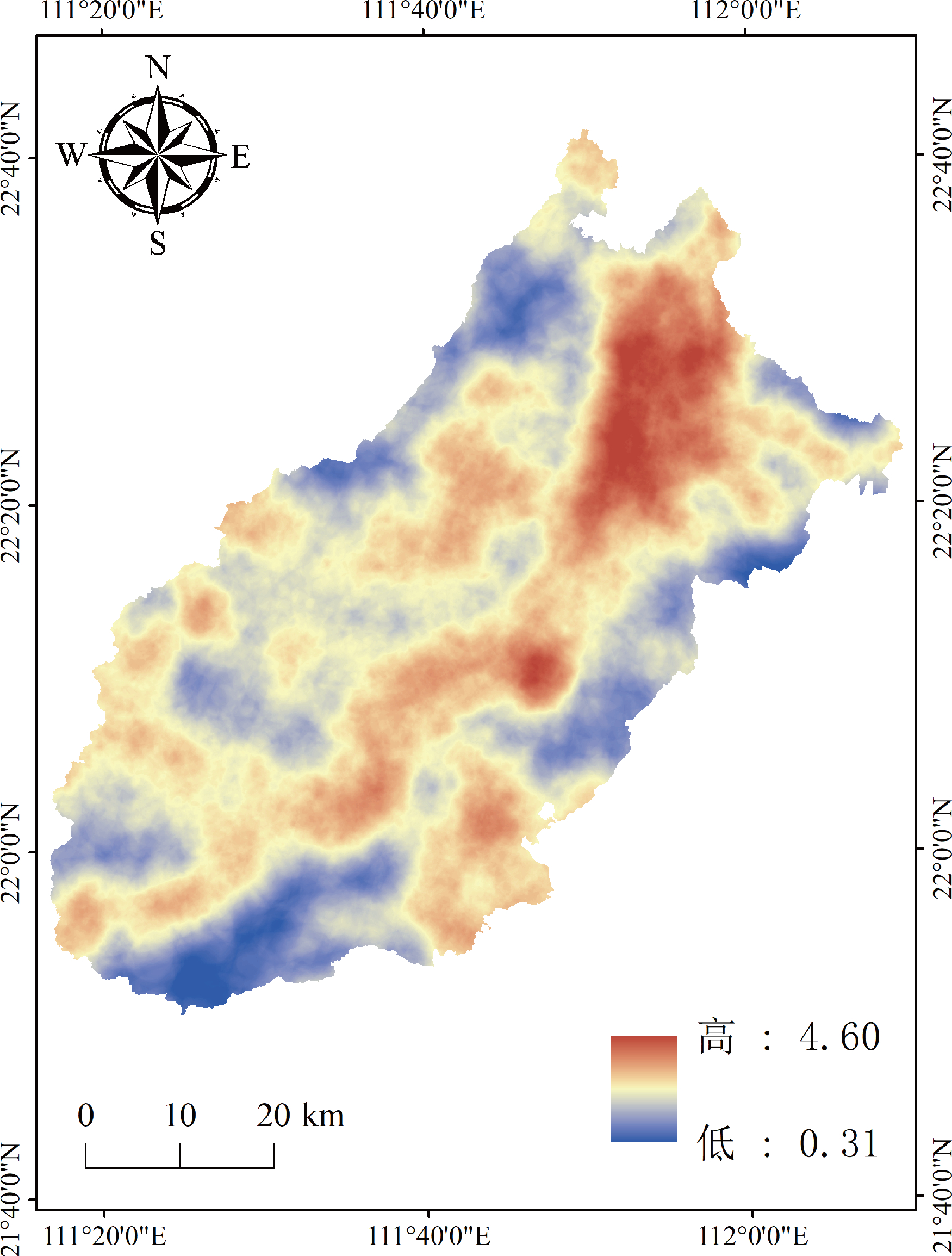
植被覆盖度影响滑坡、泥石流等地质灾害的发生与发展,主要通过间接控制降雨的留存度影响地质灾害。不同林冠对降雨的截留作用,减缓了降雨对坡体的直接冲刷,总体上植被覆盖率越高其对降雨的截留率越高,地表径流冲刷作用受限。但当降雨强度达到或超过暴雨强度时,森林对降雨的截留率减少。同等地质环境条件下植被覆盖率低,地表越裸露,地表径流冲刷作用愈强烈,滑坡等灾害较易发生。
-
图7 阳春市道路密度分布图
-
图8 阳春市工程地质岩组分布图
-
图9 阳春市距水系距离分布图
-
图10 阳春市植被覆盖度分布图
-
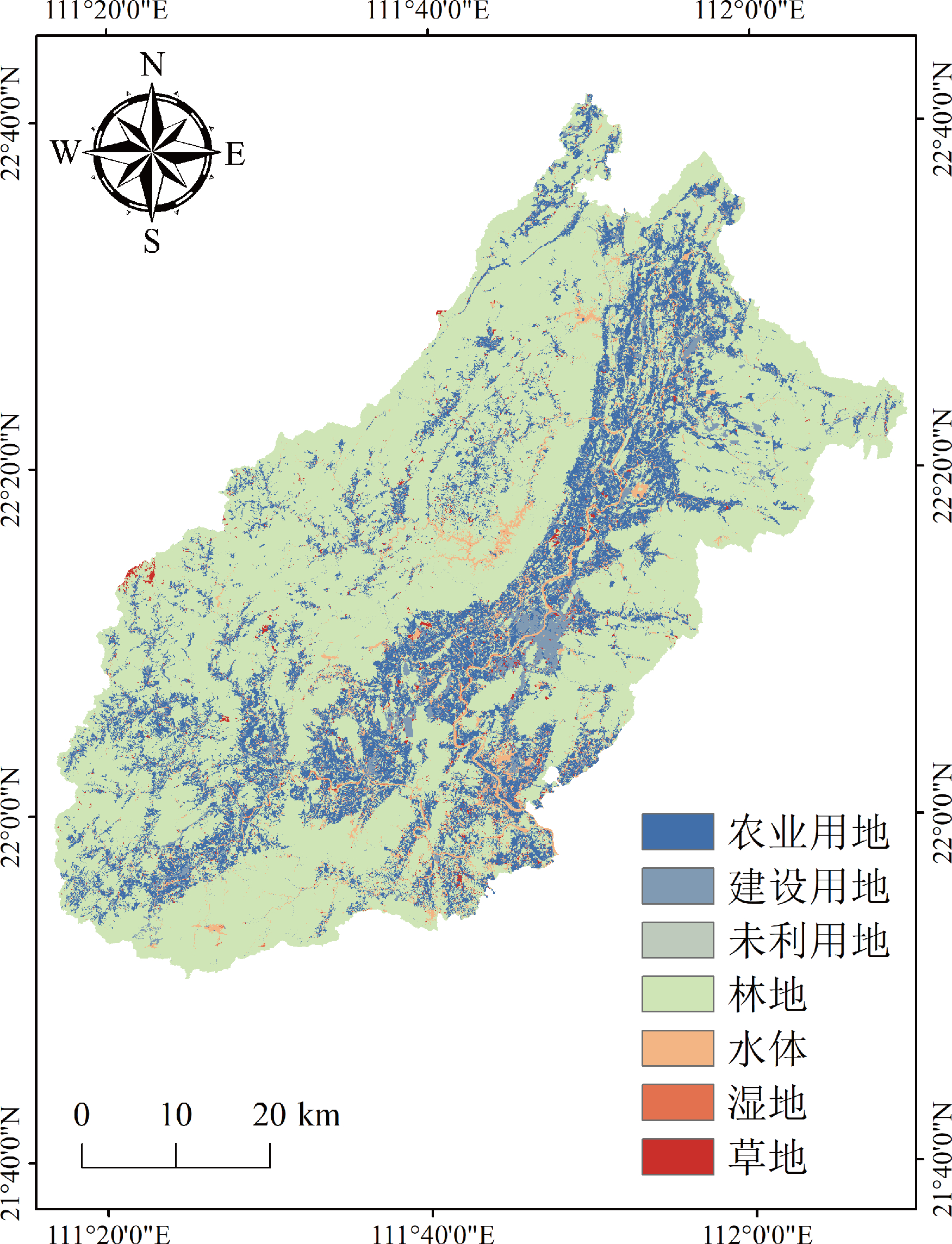
图11 土地利用类型分布图
-
土地利用现状通常代表人类活动对地表的影响程度,人类活动为地质灾害发生的主要外因和动力条件之一,且研究区已有灾害点、孕灾点威胁对象均为建成区、耕地等高价值地类。
-
利用“三调”数据库土地利用现状图,将研究区 59个小类土地利用类型,合并为7个大类,重分类并分别赋值1~7。土地利用类型重分类为农业用地、林地、草地、湿地、水体、建设用地和未利用地 7 个类别。
-
3.3 评价因子相关性分析
-
易发性评价因子之间的相关性可能会影响模型的精度。存在高相关性的因子会导致评价因子数据冗余,从而降低模型评价的精度。因此,在建立模型之前需要对因子进行相关性分析。相关性分析是一种数学统计方法,用于衡量 2 个或 2 个以上处于同等地位的随机变量之间的相关密切程度。目前主流的相关性分析方法有 3 类:皮尔逊相关系数法、肯德尔等级相关系数法和斯皮尔曼等级相关系数法。虽然它们都用于对因子进行相关性分析,但适用范围不尽相同。
-
在本文中,笔者选择采用皮尔逊相关系数法来计算变量之间的相关系数。通过计算变量的协方差与标准差之比来衡量两两变量之间的相关性。它对数据的兼容性较强,原始变量的随机分布对分析结果几乎没有任何影响。相关系数一般用符号 r 表示,给定两个随机变量 X 和 Y,r 值的计算公式如下:
-
式(1)中,n 是样本数量;Xi、Yi 是变量 X、Y 对应的i点观测值;、分别为X、Y样本的平均数。
-
相关系数 r 的取值范围是[-1,1],当 r>0 时,表示两变量正相关;当r<0时,表示两变量负相关;当r =0 时,表示两变量不相关。一般情况下,皮尔逊相关系数法仅参考相关系数r的绝对值来表示两变量的相关性等级,记作|r|,各相关性等级|r|的取值范围见表2。
-
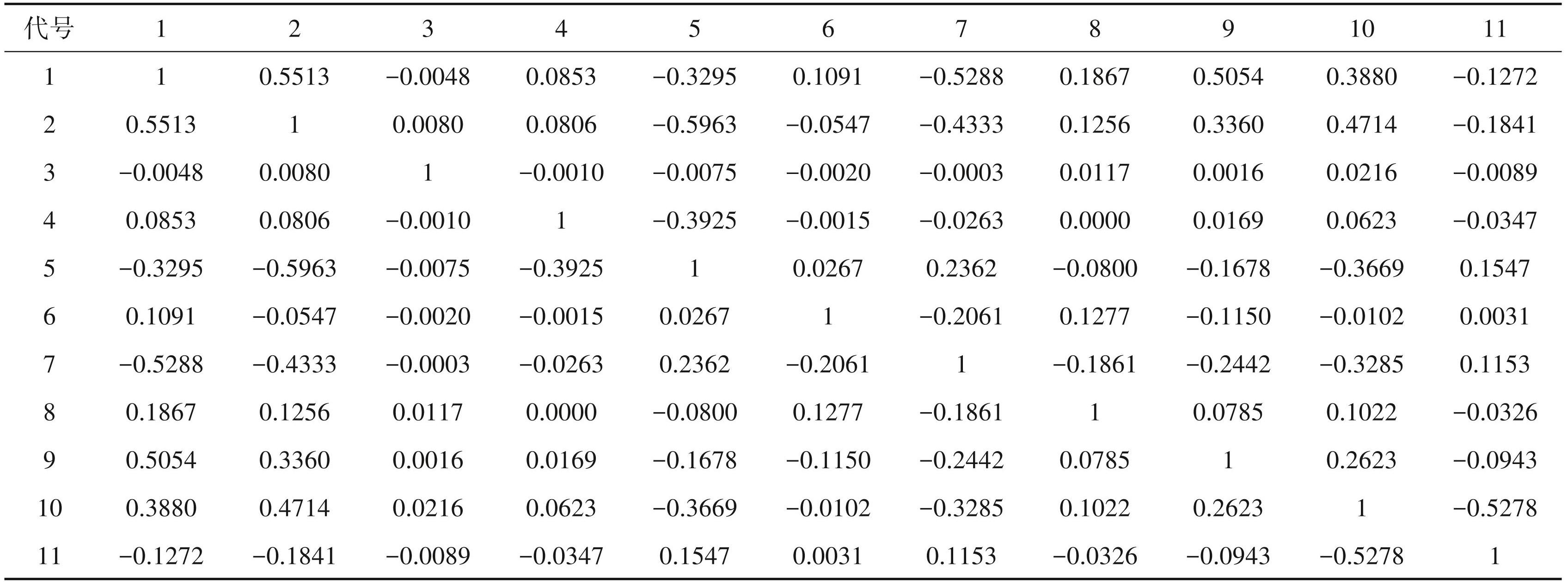
利用 GIS 空间分析工具进行分析,最终得到阳春市易发性评价因子之间的相关系数,代号对应关系为:1—高程;2—坡度;3—坡向;4—斜坡形态;5 —地形湿度指数;6—距断层距离;7—道路密度;8 —工程地质岩组;9—距水系距离;10—归一化植被指数;11—土地利用类型,结果如表3所示。
-
由表3可知,阳春市易发性评价 11个评价因子之间的相关性系数均小于 0.6,其相关性系数的众数区间为-0.30~0.30,表明上述各评价因子之间基本不相关或低度相关,评价因子之间属于相互独立关系,各因子均可用于易发性评价。
-
3.4 评价结果
-
在利用 GBDT 模型进行地质灾害易发性评价时,首先根据各因子数据制备样本数据集。根据生成的阳春市 25 m×25 m 的栅格数据,按 FID 将其转化为矢量点数据,形成样本点。通过样本点获取各个评价因子图层的对应栅格单元值,形成样本数据集。再利用灾害点和孕灾点图层获取对应空间位置的各个孕灾因子图层的栅格单元值,形成正样本数据 A。在阳春市中,从非地质灾害点空间范围内随机生成了 3 倍地质灾害编录数据的随机点,并获取对应空间位置的各个孕灾因子图层的栅格单元值形成负样本数据B。将正样本数据A和负样本数据 B 合并形成样本数据集,其中灾害数据与非灾数据的样本点数比为1∶3。
-
将样本数据集按7∶3的比例分割为训练和测试数据集,并利用梯度提升决策树模型(GBDT)进行易发性评价模型构建。在 PyCharm 编译器中,基于 Python环境调用sklearn库,调整了GBDT模型参数,最终设置为:learning_rate=0. 05,n_estimators=160, max_depth=13,min_samples_leaf=70,min_samples_ split=800,max_features=13,subsample=0.85。通过模型自带的训练精度和测试精度反馈结果为(训练精度:0.894;测试精度:0.893),这表明模型结果精度较高,适合进行易发性评价分析。
-
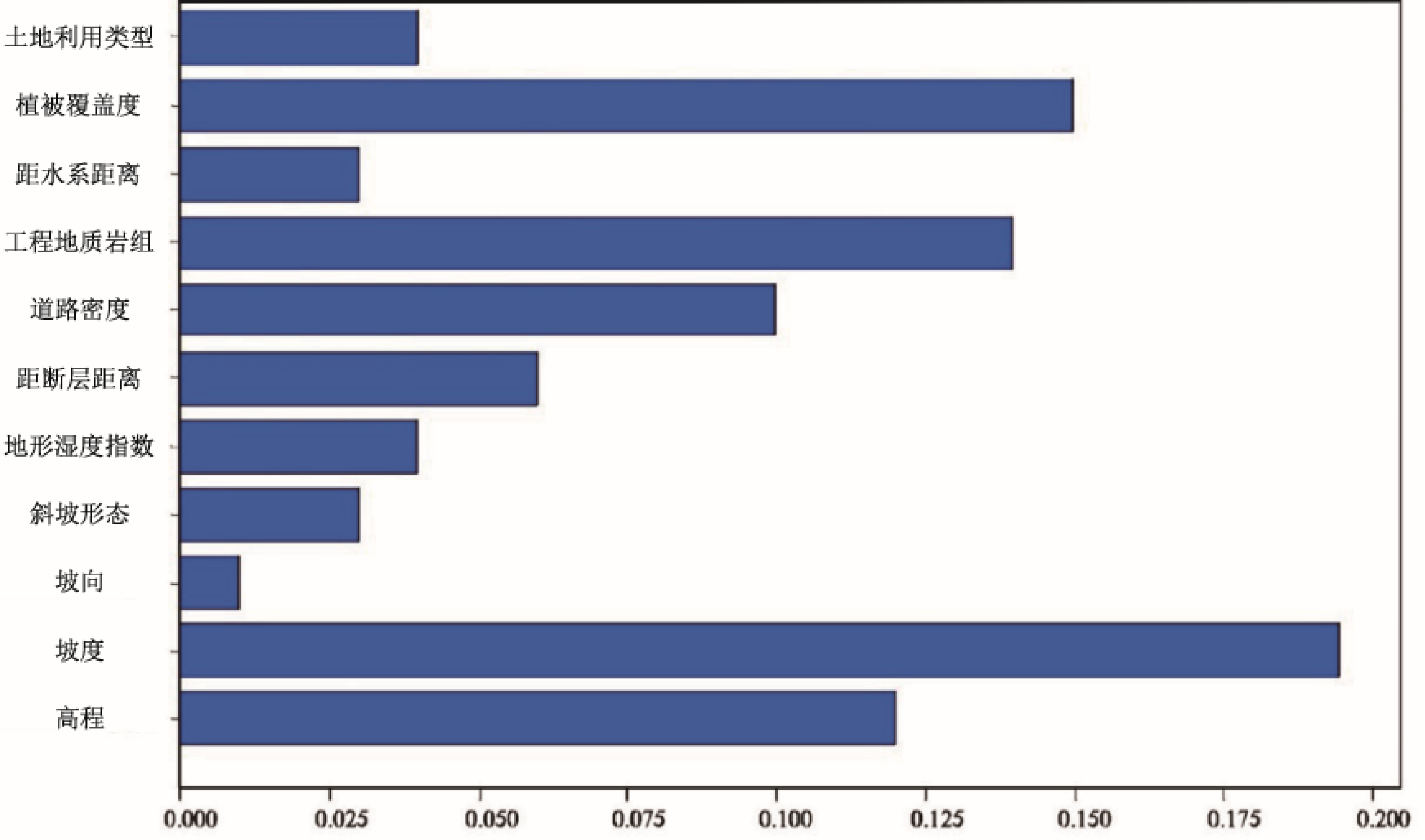
在模型训练基础上,将所有数据集导入,使用训练出的模型进行预测,并通过分类器将其映射到 0~1之间的概率值,表示易发性程度。图12显示了各评价因子的信息量大小,表明地形地貌和基础地质背景是地质灾害易发性的主要控制因素。
-
利用 GIS 分区统计,计算各灾害易发性级别所占面积和各级别中灾害栅格所占的频率比(表4)。并将分类结果利用GIS进行绘制(图13)。从表中可以看出,高易发区和中易发区的灾点占比分别达到了 23.93% 和 64.41%,两个分区灾害点占比达到了全部灾点的 88.34%,从侧面证明了本文所用方法的有效性。
-
图12 GBDT模型评价因子重要性直方图
-
图13 阳春市地质灾害易发性评价图
-
4 结果分析
-
4.1 模型精度评价
-
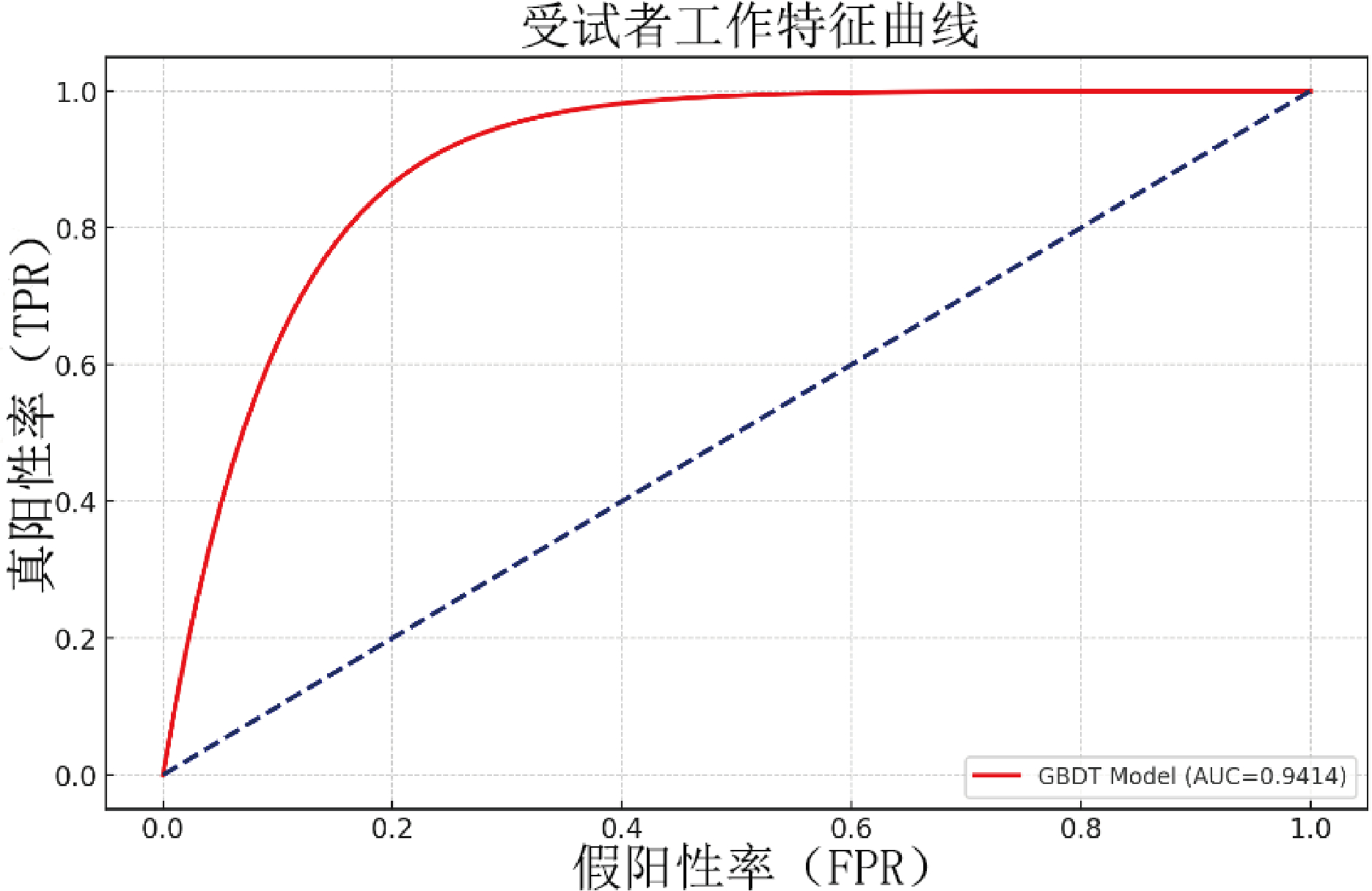
为验证所用易发性评价模型的可靠性,本次实验采用了受试者工作特征曲线(Receiver Operator Characteristic,ROC曲线)对结果进行检验。ROC曲线是地质灾害易发性评价过程中非常有效且常用的一种精度评价方法。将易发性大小等分为 30 个区间,并按易发性从大到小逐步统计易发性累计发生频率,绘制出检验样本的ROC曲线图(图14)。
-
在地质灾害易发性ROC曲线图中(图14),纵轴表示真阳性率,即实际灾害点百分比累加量,横轴表示假阳性率,即易发性面积百分比累加量。通过计算曲线下的面积(Area Under Curve,AUC),可以确定模型的模拟精度。AUC 指数是度量分类模型好坏的一个标准,其值为0.5~1,越接近1,则模型模拟值和真实值越接近。
-
基于GBDT模型的易发性评价模型得到了较高的AUC值为0.9414,显示该模型在预测地质灾害易发性方面表现优异。AUC 值作为评估分类模型性能的重要指标,表明该模型对样本数据的分类准确度较高。由于 AUC 值接近 1,表明该基于 GBDT 的评价模型具有较高的精度和较好的效果,适用于阳春市地质灾害易发性评价,可以采用该模型的结果进行地质灾害易发性分析和决策支持。
-
图14 地质灾害易发性ROC曲线图
-
4.2 易发性分区及结果分析
-
使用ArcGIS空间分析功能,提取了评价栅格单元的坡度、坡向、斜坡类型等11个指标的评价结果。再对各因子的评价结果进行归一化处理,将它们映射到 0~1 之间。最后通过栅格计算器将各因子的归一化结果叠加分析,得出地质灾害易发指数值。
-
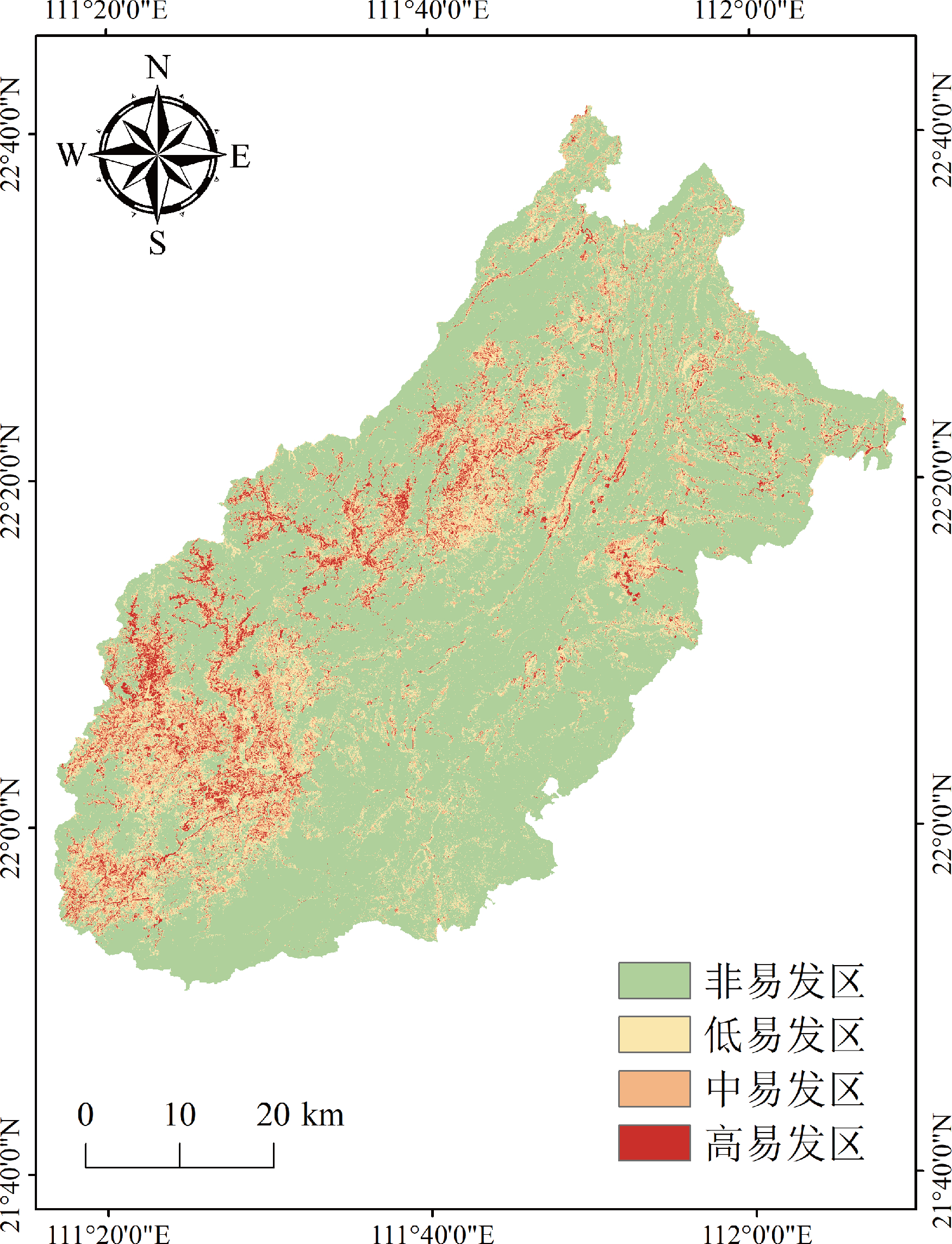
图15 阳春市地质灾害易发性分区图
-
为了将易发指数值进行直观呈现,采用了自然间断法将其分成 4 个等级,分别为:非易发区、低易发区、中易发区、高易发区,对应的指数值范围为:<-0. 013、0. 014~0. 060、0. 061~0.248、0.249~0.994。为了获得更合理的易发分区图,采用了数据分级(即专家判断法)、栅格概化及人机交互处理。最终,经过以上步骤,得到了阳春市地质灾害易发分区图(图15)。
-
经过分析,阳春市地质灾害高易发区主要集中在西部的“西山”地区,具体表现在三甲、双滘、永宁 —圭岗一带,以及马水镇石菉铜矿区和河西街道一带。这种高易发性主要由以下几个因素的综合作用:(1)地形起伏大:该地区地形起伏较大,可能存在悬崖峭壁、陡坡等地形特征,增加了地质灾害发生概率;(2)地形切割相对较强烈:地形切割指的是地质构造对地形的切割作用,可能导致地层错动、滑坡、崩塌等地质灾害;(3)人类工程活动较强烈:该地区受到较多的人类工程活动影响,如开采、挖掘、填埋等,这些活动影响孕灾地质环境条件;(4) 隐伏岩溶分布:岩溶地区容易发生溶洞、塌陷等地质灾害,如存在隐伏的岩溶,易发性将会增加。
-
综合上述因素,这些地区的地质灾害易发性较高。因此,在进行规划、工程建设以及灾害防治时,需要充分考虑这些地质灾害的风险因素,并采取相应的防范措施。
-
5 结论
-
(1)本研究选取了包括坡度、坡向、地形起伏度、工程岩组及距道路距离等在内的11种地质灾害因素,以广东省阳春市为例,探讨了梯度提升决策树(GBDT)模型在地质灾害易发性评价中的应用,经过分析认为阳春市地质灾害高易发区主要集中在西部的“西山”地区,具体表现在三甲、双滘、永宁 —圭岗一带,以及马水镇石菉铜矿区和河西街道一带。
-
(2)采用了数据分级、栅格概化及人机交互处理,分析得出阳春市地质灾害易发分区图,其中高易发区占 4.98%,中易发区占 8.42%,低易发区占 16.39%,非易发区占 70.22%。高易发性主要受地形起伏大、地形切割相对较强、人类工程活动强烈、人类工程活动影响、隐伏岩溶分布因素影响。
-
(3)利用GBDT模型,对广东省阳春市滑坡易发性进行评价。研究结果表明,模型的AUC值达到了 0.9414,反映 GBDT 模型在阳春市滑坡易发性评价中表现出较高的准确性和可靠性,可用该模型的结果为本地区提供防灾减灾决策参考。
-
参考文献
-
Catani F, Lagomarsino D, Segoni S, Tofani V. 2013. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues[J]. Natural Hazards and Earth System Sciences, 13(11): 2815‒2831.
-
Dou J, Yunus A P, Bui D T, Merghadi A, Sahana M, Zhu Z, Chen C W, Khosravi K, Yang Y, Pham B T. 2019. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan[J]. Science of The Total Environment, 662: 332‒346.
-
Friedman J H, 2001. Greedy function approximation: A gradient boosting machine[J]. The Annals of Statistics, 29(5): 1189‒1232.
-
Gao K, Cui P, Zhao C, Wei F. 2006. Landslide hazard evaluation of Wanzhou based on GIS information value method in the Three Gorges Reservoir[J]. Yanshilixue Yu Gongcheng Xuebao/Chinese Journal of Rock Mechanics and Engineering, 25(5): 991‒996.
-
Kayastha P, Dhital M R, Smedt F D. 2013. Application of the analytical hierarchy process (AHP) for landslide susceptibility mapping: A case study from the Tinau watershed, west Nepal[J]. Computers & Geosciences, 52: 398‒408.
-
Kim J C, Lee S M, Jung H S, Lee S. 2017. Landslide susceptibility mapping using random forest and boosted tree models in PyeongChang, Korea[J]. Geocarto International, 33(9): 1000‒1015.
-
Othman A, Gloaguen R. 2014. Improving lithological mapping by SVM classification of spectral and morphological features: The discovery of a new chromite body in the mawat ophiolite complex (kurdistan, NE iraq)[J]. Remote Sensing, 6(8): 6867‒6896.
-
Pourghasemi H R, Moradi H R, Aghda S M F. 2013. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances[J]. Natural Hazards, 69(1): 749‒779.
-
Pourghasemi H R, Pradhan B, Gokceoglu C. 2012. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz watershed, Iran[J]. Natural Hazards, 63(2): 965‒996.
-
Sevgen E, Kocaman S, Nefeslioglu A H, Gokceoglu C. 2019. A novel performance assessment approach using photogrammetric techniques for landslide susceptibility mapping with logistic regression, ANN and random forest[J]. Sensors, 19(18): 3940.
-
Song Y, Niu R, Xu S, Ye R, Peng L, Guo T, Li S, Chen T. 2018. Landslide susceptibility mapping based on weighted gradient boosting decision tree in Wanzhou section of the Three Gorges Reservoir Area (China)[J]. International Journal of Geo-Information, 8(1): 4.
-
Wang J, Yin K, Xiao L. 2014. Landslide susceptibility assessment based on GIS and weighted information value: A case study of Wanzhou district, Three Gorges Reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 33(4): 797‒808.
-
Yoshimatsu H, Abe S. 2006. A review of landslide hazards in Japan and assessment of their susceptibility using an analytical hierarchic process (AHP) method[J]. Landslides, 3(2): 149‒158.
-
陈涛, 朱丽, 牛瑞卿 . 2018. 基于 GBDT 模型的滑坡易发性评价 [C]//高分辨率对地观测学术联盟 . 第五届高分辨率对地观测学术年会论文集 . 中国地质大学(武汉)地球物理与空间信息学院, 511‒520.
-
方浩, 高姣姣. 2012. 油气长输管道滑坡地质灾害危险性评价专家系统研究[J]. 水文地质工程地质, 39(4): 126‒131.
-
康超, 谌文武, 张帆宇, 和法国, 宋丙辉. 2011. 确定性模型在黄土沟壑区斜坡稳定性预测中的应用[J]. 岩土力学, 32(1): 207‒ 210, 260.
-
刘坚, 李树林, 陈涛 . 2018. 基于优化随机森林模型的滑坡易发性评价[J]. 武汉大学学报(信息科学版), 43(7): 1085‒1091.
-
马彦彬, 李红蕊, 王林, 仉文岗, 朱正伟, 杨海清, 王鲁琦, 袁兴中. 2022. 机器学习方法在滑坡易发性评价中的应用[J]. 土木与环境工程学报, 44(1): 53‒67.
-
盛明强, 刘梓轩, 张晓晴, 胡松雁, 郭子正, 黄发明. 2021. 基于频率比联接法和支持向量机的滑坡易发性预测[J]. 科学技术与工程, 21(25): 10620‒10628.
-
宋英旭 . 2019. 基于空天地一体化监测的滑坡风险动态评价研究 [D]. 武汉: 中国地质大学.
-
田利川, 姜建梅. 2008. 基于滑坡水文耦合模型的区域斜坡稳定性研究[J]. 资源环境与工程, 22(2): 208‒212.
-
王佳佳, 殷坤龙, 肖莉丽 . 2014. 基于 GIS 和信息量的滑坡灾害易发性评价——以三峡库区万州区为例[J]. 岩石力学与工程学报, 33(4): 797‒808.
-
向喜琼, 黄润秋 . 2000. 基于 GIS 的人工神经网络模型在地质灾害危险性区划中的应用[J]. 中国地质灾害与防治学报, (3): 26 ‒30.
-
许冲, 戴福初, 姚鑫, 陈剑, 涂新斌, 孙瑜, 王志一. 2009. GIS支持下基于层次分析法的汶川地震区滑坡易发性评价[J]. 岩石力学与工程学报, 28(S2): 3978‒3985.
-
许英姿, 卢玉南, 李东阳, 陈立华. 2016. 基于GIS和信息量模型的广西花岗岩分布区滑坡易发性评价[J]. 工程地质学报, 24 (4): 693‒703.
-
余坤勇, 姚雄, 邱祈荣, 刘健 . 2016. 基于随机森林模型的山体滑坡空间预测研究[J]. 农业机械学报, 47(10): 338‒345.
-
摘要
本研究旨在利用梯度提升决策树(Gradient Boosting Decision Tree,GBDT)模型,对广东省阳春市滑坡易发性进行评价。通过收集大量地质、地形、气象等相关数据,提取了坡度、坡向、工程岩组等11个地质灾害易发性评价指标,构建了全面的滑坡易发性评价指标体系,并采用GBDT模型进行训练和预测。受试者曲线 (Receiver Operator Characteristic,ROC曲线)和AUC值(Area Under Curve,AUC)被用于评估模型的准确性,研究结果表明,模型的 AUC值达到了 0. 9414,说明 GBDT模型在阳春市滑坡易发性评价中表现出较高的准确性和可靠性。易发性分区统计结果显示,整个阳春市中,高易发区占 4. 98%,中易发区占 8. 42%,低易发区占16. 39%,非易发区占70. 22%。本文研究方法可为开展区域地质灾害易发性评价提供参考。
Abstract
This study aims to use the Gradient Boosting Decision Tree (GBDT) model to evaluate the landslide susceptibility in Yangchun City, Guangdong Province. A comprehensive system of evaluation indicators for geological disaster susceptibility was constructed by collecting a vast amount of geological, topographical, and meteorological data and extracting 11 key indicators, such as slope, aspect, and engineering rock group. The GBDT model was trained and predicted using these indicators. The accuracy of the model was assessed using the Receiver Operator Characteristic (ROC) curve and the Area Under Curve (AUC) value. The results showed that AUC value of the model reached 0. 9414, indicating high accuracy and reliability of the GBDT model in evaluating landslide susceptibility in Yangchun City. The statistical results of susceptibility zoning showed that in the entire study area, highly susceptible areas accounted for 4. 98%, moderately susceptible areas for 8. 42%, low susceptibility areas for 16. 39%, and non-susceptible areas for 70. 22%. The research method of this paper can be used for the evaluation of regional geological disasters.