0 引言

建设工程中，偏心有几何形态的偏心和受力作用下的偏心，既然有了几何的偏心，就会有偏心距，在力学体系里，也就有了偏心矩，也就是说：工程上的偏心距是偏心受力构件中轴向力作用点至截面形心的距离，而偏心矩是合受力中心到支承点距离与合受力乘积的矢量值。偏心随时存在于建设工程中，由于结构形体偏心存在，故在内外力作用下产生了偏心矩，偏心矩在地面空间、地下空间都存在；同时在房建工程、地下通道工程隧道同样存在。而正因偏心现象的存在，所以导致建设工程出现偏心力矩，当整个工程的力学重心偏移基础宽度一定值时，则产生工程整体不稳定，随时因力学体系改变而失稳；在实际结构中，理想的轴心受压构件是不存在的（张卫民等，2020），由此可见，偏心现象存在于任何建设工程中。

而分析偏心问题方法，多见建立于理想模拟数值分析，拟以非线性有限元分析软件为平台，建立如钢管高性能混凝土偏压构件的有限元分析模型 （于清等，2009）。应该指出：上述的分析是在理想条件进行的，例如假定洞壁各点的径向位移都相同、假定支护需求曲线和支护刚度无关等（彭琦， 2008）。但实际工程施工中，在塑性工程的岩土力学作用则受围岩体的地下水、裂隙分布、层厚，以及各个岩土力学指标复杂的叠加影响，而弹性工程同个构件则受屈服强度、弹性系数不均分布及各种不同轴面惯性矩分布影响，力学规律只是按实际条件发展，而理想假设只能使分析理论尽可能趋于精确，以至成为设计和解决问题的一种途径；然而，实际工程中最重要的是以现场实测为依据，在试验数据分析的基础上，根据应变协调条件（于峰等，2014）。

建设工程未超出限值的偏心属于小偏心，而超出限值的属于大偏心；小偏心无处不在，超限值的大偏心也很常见，以致工程失稳现象经常发生，其中质量安全隐患随时存在。在实际工程须解决，以研究偏心力学因素为突破口，以各种力学因素在整个体系中相关性、分项性能指标重要性、等效性，从中研究出相关的趋于精确、能以数学表达描述的数学计算式，推定解决偏心问题的方案，从而以准确的方法验证方案的实施效果。但不管如何结合实测，运用实测值进行数学模拟，反证方案实施的可靠性和实效更显重要。所以，本文欲通过运用此数学理念进行建设工程的偏心距和偏心矩分析，揭示消除因偏心而导致的工程隐患，进一步阐明解决偏心问题的理论依据。

1 建设工程偏心的分类

在一形态体系中，因形态分布不均匀内力作用或是受外力而导致偏心距和偏心矩的产生。从而，在同一形态物体中，由于存在质量分布均匀而出现质量偏心；由于同一平面内构件受荷不均衡而导致刚度偏心；由于同一构件受荷屈服强度不一致而导致强度偏心；所以，建设工程偏心可分质量偏心、刚度偏心，强度偏心 3类。受力之下，此 3类偏心现象均产生偏心力矩。但本文侧重研究质量偏心距和偏心矩。

2 建设工程质量偏心现象的形式

建设工程的质量偏心现象既可以存在地面工程，也可以存在地下工程；建设工程质量偏心现象既可以因工程构件复杂构成形体偏心，也可以是因外力作用、并形成合力作用偏离形体中轴线的偏心。

地面工程存在偏心即可以由建筑结构设置如挑臂梁悬臂结构、或局部受外水平力以及外竖向压力作用所导致；而建设工程的基础工程中所存在的偏心，则是因构筑物形心不对称或是受水平土压力作用所导致；而地下空间工程中所存在的偏心，如隧道工程，则是存在构筑物形心不对称或受水平岩土压应力作用导致的质量偏心现象。而本文则着重阐述工程构造形态分布和受力作用不均的力学机理，并阐明其所带来的病害，总体来说，此类病害因局部压应力作用而形成的应力集中，造成偏心距 e 绝对值过大，所引发的不均匀沉陷和坍塌（姚祖康，1993）。

建设工程质量偏心现象问题很多，在此运用基础工程和支护工程力学分布与作用机理，分析因偏心距存在给永久性工程带来的诸多损害，下文将分别分析汕汾高速和揭普高速的软基段桥台超载预压偏心导致地拱和桥台桩基被压倾斜问题，以及博深高速杨岗 1^＃隧道工程的偏压造成隧道拱环结构偏心现象的问题。

3 建设工程质量偏心距问题分析

一般地，若是体系受力处于极限平衡之内，则形心只出现偏差现象，仍在允许的范围，未致体系失衡；若是体系受力超出极限平衡状态，则致形心偏离于允许的界限，而出现体系失衡，导致体系破裂解体。

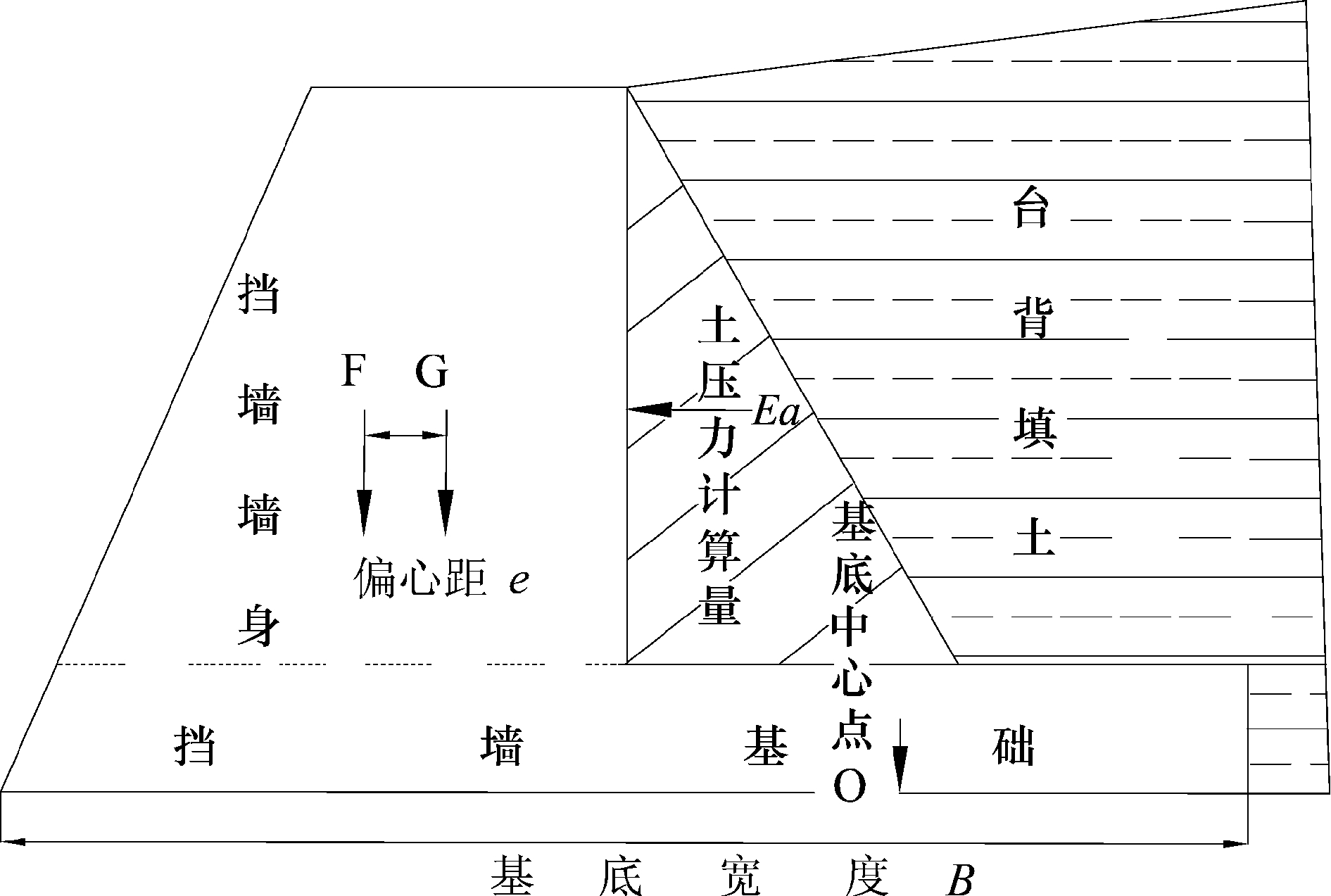
行业规范中，偏心距 e，支挡构件基底宽度 b，e 值不能超出 b 值的 1/6（广东省住房和城乡建设厅， 2016）。理想模式里，也就是在假定的匀布受力空间内，以支挡结构基底宽度的中点为区间 0 点，在$\left\{-\frac{b}{6}，\frac{b}{6}\right\}$区间，支挡结构基底所承受荷载不能超出地基承载力的 1.2 倍。在实际计算上，首先须确定几何形心和重心的位置，若是体系为单个规则的几何形体，则通过几何计算而确定重心；若是体系为若干规则的几何单体叠加，则分解为若干规则的几何单体，通过力矩平衡方程求解确定重心；若是体系为不规则的几何形体，则需分解为若干的近乎于规则的几何单体，通过力矩平衡方程、运用微积分求得单体近乎于规则体的几何重心，然后叠加合成求得不规则体的几何重心（图1）。

假若（梯形上底+梯形下底）/2×高×x＝矩形底边×高×（三角形底边＋矩形底边一半）＋1/2×三角形底×高×直角三角形底边×2/3，可求得 x 值，x 为挡土墙整体重心与支点的距离（m）；假若在整个支挡结构抗倾覆体系中，力矩支点也就是直角三角形底边的端点，挡土墙基础宽度等于直角三角形与矩形两底边之和；那么，挡土墙的重力作用线由于多形体叠加所产生的偏心距离，此距离就是重力偏心力臂，其值 x 为基础宽度一半。若竖直向未出现其他荷载时，高边坡的土压力就是使支挡体系产生偏心距的另一因素，土压力作用而导致支挡体系产生偏心力矩，土压力作用线与作用点（支挡结构底边中点）的距离即为土压力作用力臂。

由此，验算判别支挡结构体系抗倾覆稳定性，但首先必须验算偏心距是否满足处于规范要求的限定$\left\{-\frac{b}{6}，\frac{b}{6}\right\}$的区间内，以及验算地基荷载是否满足不超出规范的要求。控制偏心距小于支挡结构基底宽度的 1/6是结构体系具有抗倾覆和稳定性的必要条件，在偏心距符合规范要求的前提下，如果结构体系偏心力矩引起的地基荷载最大值仍处于 1.2 倍地基承载力内，那么抗倾覆稳定性的验算判别条件成立，也就是首先具备偏心距小于 b/6 和地基最大荷载小于 1.2 倍地基承载力的两必要条件，才能进行抗倾覆稳定性的验算判别。然而，当偏心距在$\left\{-\frac{b}{6}，0\right\}$半区间里，即是偏心距为-e时，在偏心力矩将引起的地基荷载产生增量条件下，地基荷载最大值能否控制于 1.2 倍地基承载力内（常士骠和张苏民，2007），也必须纳入验算分析程序。

4 建设工程基础和支护结构质量偏心分析

建设工程质量偏心现象普遍存在于任何工程中，其所造成的工程病害轻重不一，对基础工程和支护工程危害性较大。基础工程常见有软基段的桥台超压，由于偏心土压力作用，导致周边地基地拱和桥台桩基倾斜垮塌；支护工程常见有隧道支护拱环的坍塌，仰拱变形起拱的破坏性极高。

基础工程中软基段的桥台需超高堆载预压，因土体堆载造成质量偏心，使得土压应力局部集中，除可能导致桥台坍塌外，还存在周边地基地拱风险，严重危害周边构筑物使用及生命安全（黄朝煊等，2021）。

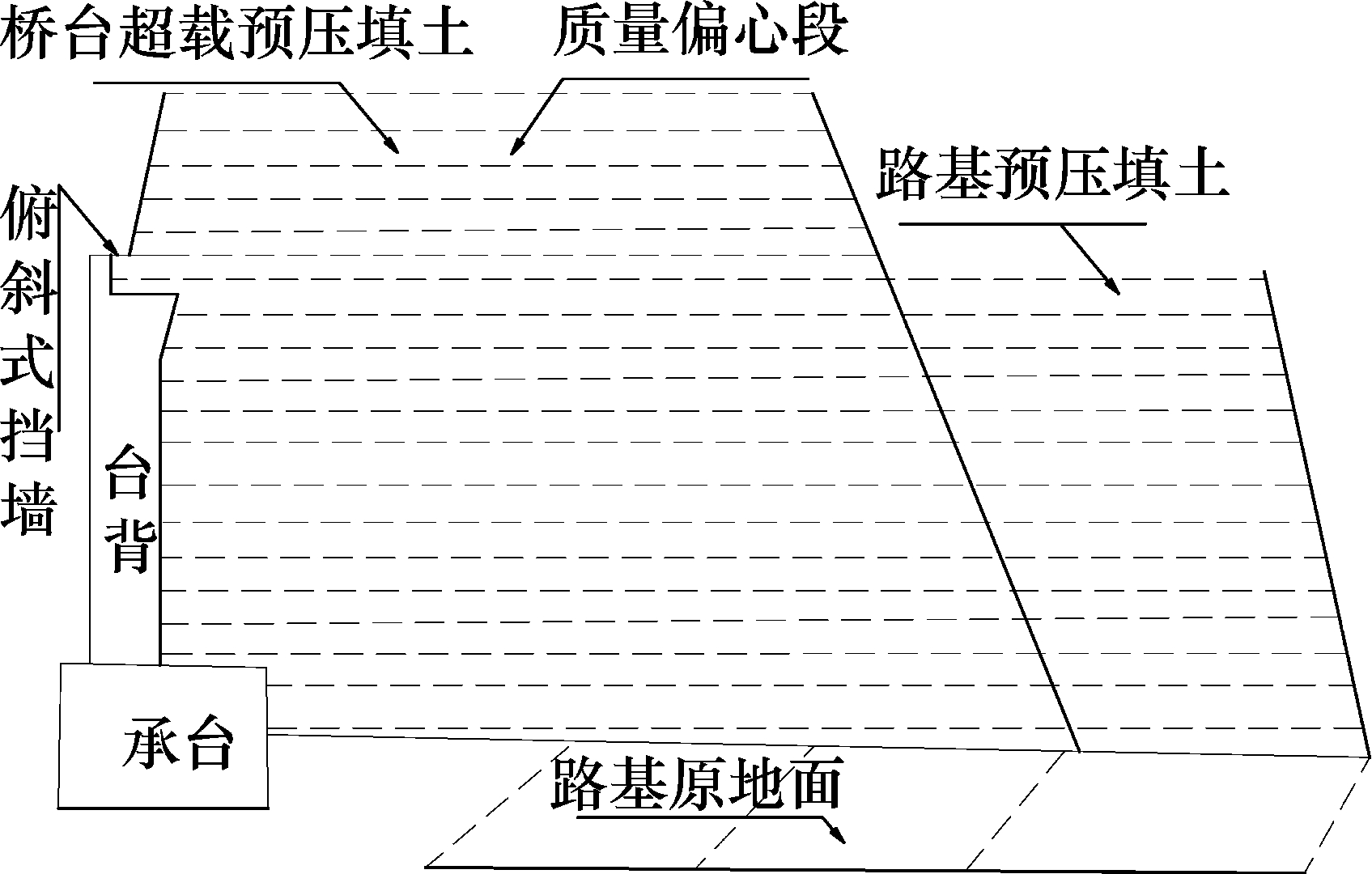
软基段桥台超载预压多见于高速公路工程中，处于沿海高速的汕汾高速公路和揭普高速公路，软土淤泥层分布广、层厚巨大，工程力学指标极差，软土的含水量超过 95%，揭普高速公路的霖磐段淤泥的含水量因其混有大量的腐殖物，故都超过 100%。软土淤泥层厚15～30 m，地基承载力都未达30 kPa，桥台超载预压的土层大都超过15 m，预压土层的孔压观测标高超过附近民居的 6 层楼顶，由此出现了路基堆载预压的质量偏心段，由于上填层巨厚，预压土在基底集中巨大附加应力，造成软基侧向变形对邻近桥台及桩基有直接影响（谢洪涛和杨春和， 2002），其表达式为附加应力 σ=kγH，k 为竖向附加应力系数、γ 为预压土容重、H 为预压土上填净厚度。虽然严格控制预压土的上填速率、桥台的施工时间，但肋式桥台的排桩还是被挤而出现倾斜；桥台坡脚地面，为隔离堆载预压的水平剪切力而挖出多道剪力沟，但周边的民居平房墙体还是因地拱而抬升变形、出现剪性裂缝；其剪性裂缝就是堆载预压所出现质量偏心距和偏心矩，导致出现质量偏心病害。桥台预压质量偏心段如图2所示。

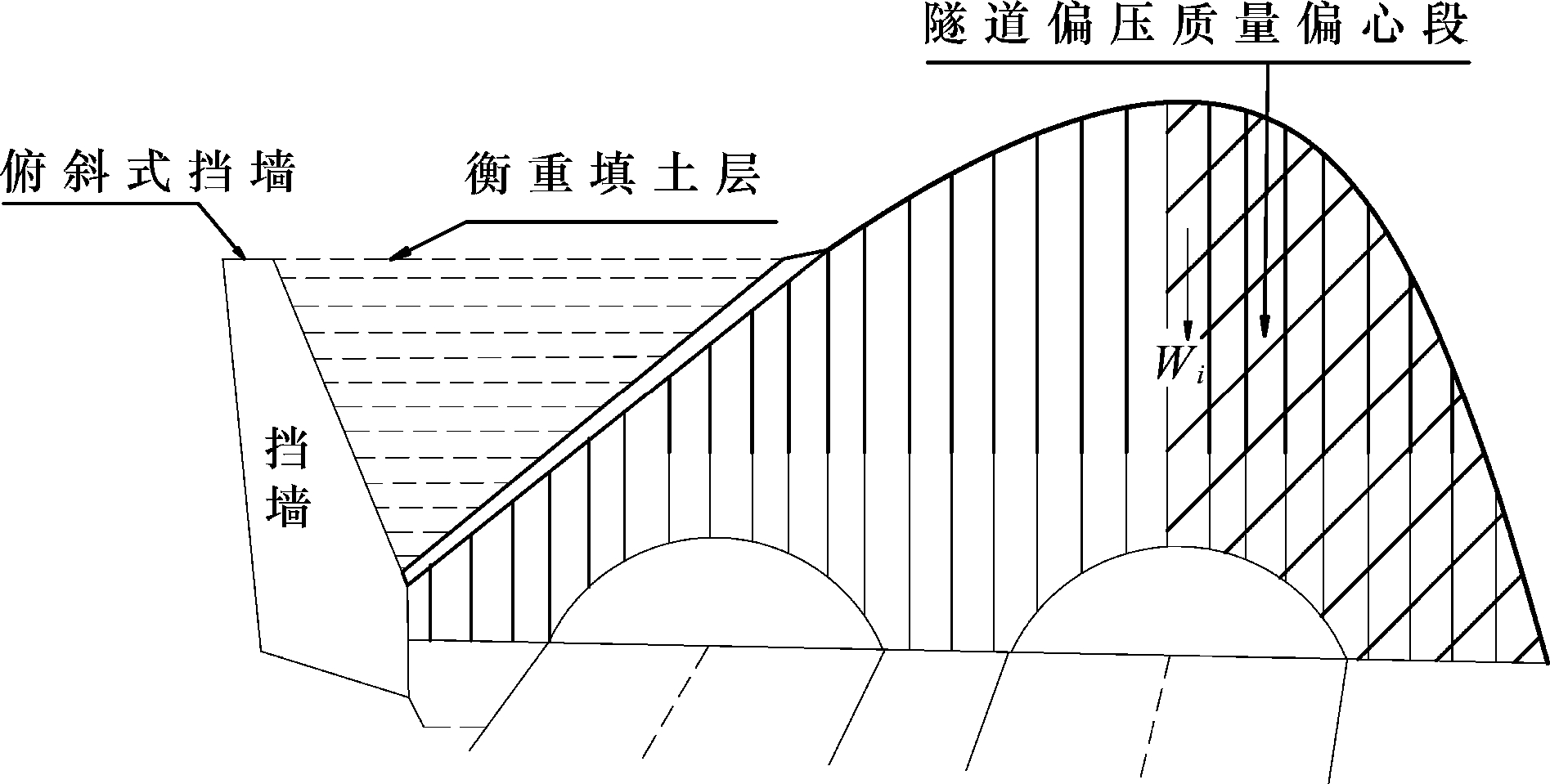
支护工程中，偏心最常见于隧道工程。暗洞的拱环，明洞的边墙，洞顶支撑梁、底板等，隧道洞内结构都需要受围岩的岩土压力作用，对于拱顶或支撑梁则受竖向与水平向的围岩土压力作用，而边拱或边墙则受围岩的水平土压力，至于仰拱或底板则受隧道下围岩和地下水的上拱的压力。从力学作用上讲，以拱环为中心，各方的受力方向是相反的，而大小则基本相等，从而具有闭合拱环的隧道，把各向受力转化为作用于同一轴面的轴力，基本可相互抵消，处于相对平衡稳定状态。然而，若是拱顶及边墙的某一方存在较高凸起围岩，那么凸起围岩则形成形体偏心，土压应力则形成偏压，也就此构成隧道的偏压段。由于偏压段存在，导致隧道拱顶出现质量偏心距和偏心矩，导致出现质量偏心病害。隧道偏压质量偏心段如图3所示。

5 隧道偏压段质量偏心的力学分析

5.1 偏心距与隧道偏压偏心力学关系

偏心距在物体形态上，属于中心偏离的几何参数，而在力学里，由于内力和外力作用，则是把形态存在的几何偏心距参数演变成一个力学作用的参数——偏心矩。

隧道工程，因交通轴线两侧存在不对称围岩压应力，而必然出现偏压，特别是山地隧道和海底隧道，经常在边仰坡出现偏压现象，且由于偏压而导致作用于隧道洞身的土压应力集中，出现围岩体重心偏离，因此而存在偏心距。也就是说因为隧道的偏压才造成偏心距的存在，在围岩土压应力的作用偏心力矩也就出现。

偏心距在建造物的上构存在，在建造物的基础中也必定存在；在地面建筑空间存在，在地下空间也必定存在。隧道岩土工程属于地下通道工程，属于地下空间建筑，如今隧道结构多种多样，可以山地隧道、海底隧道，而此两种隧道受结构物外岩土体和水体不均匀或偏离中心的土力学作用，形态上就会出现偏心距几何量数，力学里则会出现偏心矩力学参数（孙闯等，2023）。

在博深高速的龙岗1^＃隧道的勘察设计阶段，为研究已初步设计龙岗 1^＃隧道偏压围岩段对隧道拱圈的应力动态，对初步设计的隧道拱顶处的围岩取多个实测断面，采取钻孔进行现场原位试验。在初步设计的隧道拱顶相应标高，采用盲孔应力检测法，以初步设计隧道拱顶为中轴线，在同一断面内，分别在两侧拱肩各布置7个隧道拱肩竖向应力观测点，并且把两侧拱肩分为向偏压面和背偏压面，以近拱顶为第一检测点，远离拱顶向依次排序到第七点，点号为 d _向和 d _背。向偏压面检测值：σ_{d 向1}= 1537. 0 kPa、σ_{d 向2}=1471.4 kPa、σ_{d 向3}=1511.7 kPa、 σ_{d 向4}=1479.3 kPa、σ_{d 向5}=1499.8 kPa、σ_{d 向6}=1503.5 kPa、σ_{d 向7}=1547.1 kPa；背偏压面检测值：σ_{d 背1}= 518.4 kPa、σ_{d 背2}=499. 0 kPa、σ_{d 背3}=475.6 kPa、σ_{d 背4} =445.9 kPa、σ_{d 背5}=335.5 kPa、σ_{d 背6}=303.9 kPa、 σ_{d 背7}=391.3 kPa。而每个断面的向偏压面和背偏压面同一数位点 n 是对称的，在此以同一数位点作对比，求出其比例系数，ν_n=σ_{d 向n} /σ_{d 背n}，即 ν₁=2.96、ν₂= 2.94、ν₃=3.18、ν₄=3.31、ν₅=4.47、ν₆=4.95、ν₇=3.95，自上计算可知，未经处理的隧道拱肩偏压明显，工程质量偏心隐患严重。

5.2 隧道偏压偏心段岩土特征

在项目工程的隧道偏压实际研究中，以博深高速公路的杨岗 1^＃隧道岩土工程为例。博深高速公路杨岗 1^＃隧道洞口处于多级边坡的中、下台级上，洞口工程处于山地坡脚，洞口围岩可见严重偏压，并且属于埋深小于 40 m 浅埋段，洞口边仰坡坡率大，边仰坡土层为巨厚风化层覆盖的植皮台级的山地坡体。坡体岩土层构成由上而下分别为耕作土、含砾黏土，风化残积层的砂质黏性土，强风化、中风化花岗岩和微风化花岗岩构成。

根据现场岩土勘察的土力学指标平均值：表层土为含砾黏土，最大层厚 7. 00 m，含水量 ω = 27.58%，湿密度ρ=1.92 g/cm³，孔隙比e=0.809，液性指数 I_L=0.81，内摩擦角 ϕ=14.7°，黏聚力 c=15.3 kPa，压缩模量 E_S=2. 01 MPa，下覆层为砂质黏性土：最大层厚 23. 00 m，含水量 ω=20.51%，湿密度 ρ= 1.95 g/cm³，孔隙比e=0.601，液性指数I_L=0.17，内摩擦角 ϕ=18.7°，黏聚力 c=14.33 kPa，压缩模量 E_S= 4.35 MPa，按隧道工程的围岩软硬等级分法，自上试验参数描述的两土层都属于六级软弱围岩（王毅才，2006），围岩特征如图4所示。

5.3 隧道偏压偏心段岩土工程土力学分析

隧道围岩偏压体也是质量偏心现象，岩土体的偏心距超出极限平衡影响稳定性的病害，如下进行土力学体系平衡稳定性分析。

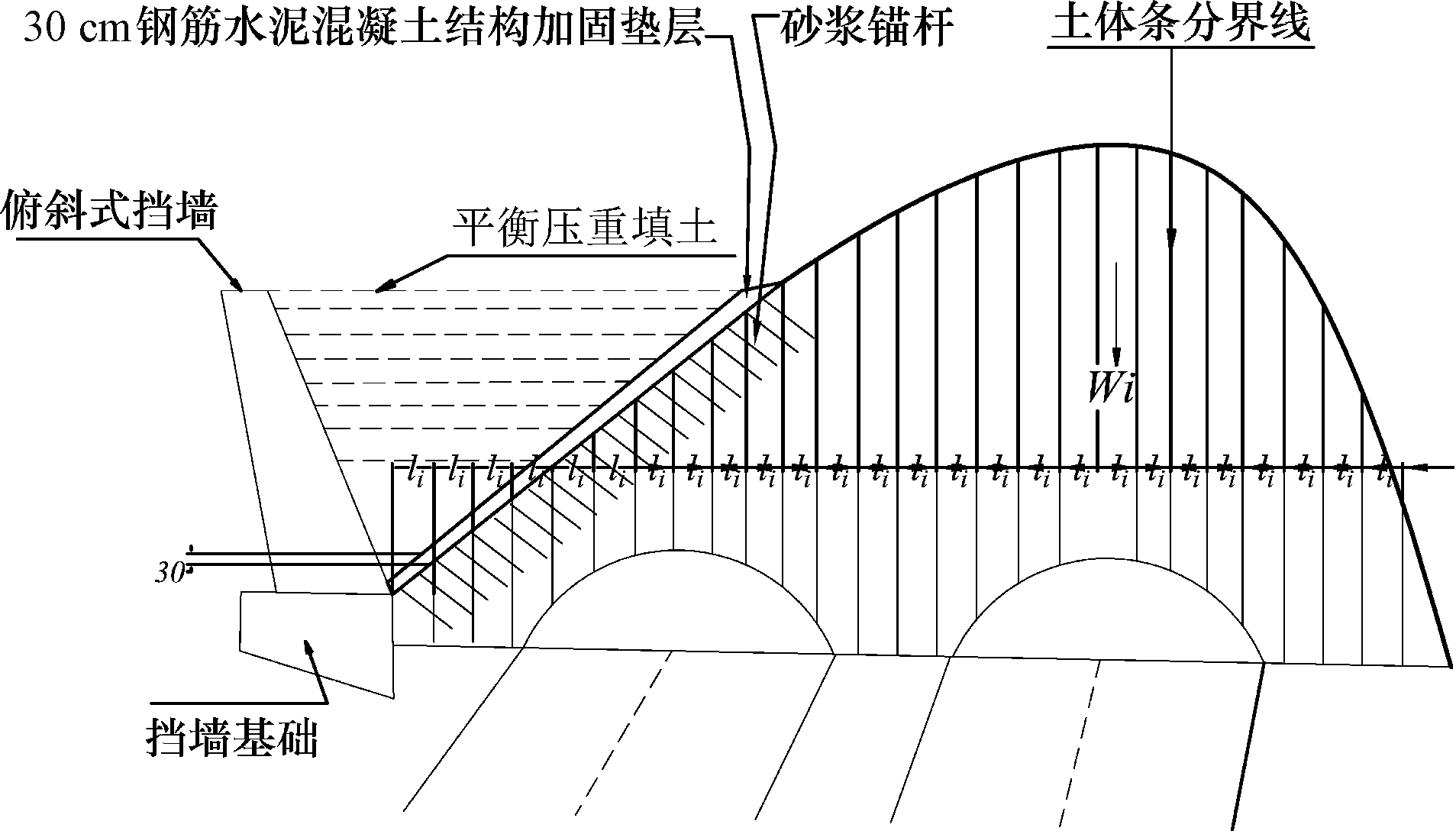
首先必须进行隧道洞口围岩岩土体偏压体精确的力学参数量测和土力学分析。荷载原剪切平衡面处于平衡压重填土的基底原地面应精确测量； 其次，根据隧道洞口隧道工程的岩土勘察结果，把偏压围岩土体按不同容重岩土体细划成近似规则几何形状的单元体分区，再次，按每个单元体分区单位长度的近似几何形状面积所对应的方程函数微积分，求出每个单元体分区单位长度几何体截面面积，由此，根据其所相应容重（γ_i）推算出每个单元体分区自重，假若岩土体取单元体，那么对于任何 i 有l_i =1，其中，每个单元体分区岩土体内摩擦角（ϕ_i）、黏聚力（c_i）和工程设计施工要求的安全系数（F），可根据岩土勘察、现场实测结果以及设计要求获得； 从而，推算出隧道工程偏压围岩土体滑移力（P），验算隧道岩土体整体稳定性（图5；李广信，2004）。

偏压岩土体土力学因素有：N 个单元体分区自重（W_i）的和总重（W）、N 个单元体分区的侧向剪切应力（T_i）——岩土的剪切应力（T_i）的和总剪切应力 （T）和上个单元体分区连续传递的滑移力 P_i-1cos （α_i-1-α_i）； 假设偏压岩土体受力达到塑性极限平衡状态的侧限的被动土压力（σ₃），即将变形位移之前的平衡状态，偏压岩土体总重（W）、单元体分区连续传递的滑移力 P_n-1和总剪切应力（T）的合力便是隧道工程偏压围岩土体滑移力（P）。

根据土体稳定性分析的条分法和传递系数法有：P_i =W_i sinα_i +P_i-1cos（α_i-1-α_i）-T_i，其中，T_i =（C_il_i + N_itgφ）/F、N_i =W_icosα_i +P_i-1sin（α_i-1-α_i）、P_n-1=P_n-2cos（α_i-2-α_i-1）。因此，P=W_nsinα_n+P_n-1+T_n-1，若 P≤0，则隧道偏压岩土体稳定；反之隧道偏压岩土体不稳定 （王毅才，2006）。

实际上，隧道工程偏压围岩土体滑移力（P），是由于每一土条偏心产生偏心距，导致下滑趋势产生，这些偏心距的叠加，成为岩土体下滑总的趋势，即总的偏心距，导致围岩土体产生总的滑移力，滑移力就是偏心矩，围岩土体因偏心矩作用而失衡不稳定，因此，隧道围岩土体偏压同样是由于岩土体偏心距导致直接影响其稳定性。

5.4 隧道偏压偏心段加固岩土工程力学分析

面对隧道围岩土体因偏心距影响其稳定性的病害，须设法使将要变形而未完全变形的软弱岩土体获得新的塑性应力以达到平衡，设置等效于加固的工程，如在地表设置砂浆锚杆，并在设置砂浆锚杆后铺设一层或多层的钢筋网水泥混凝土结构层，使之与地表砂浆锚杆构成整体。地表设置砂浆锚杆土力学作用同于隧道工程初期支护的系统锚杆，加固围岩，使围岩的土力学性质得到改善和抗剪强度加强，围岩整体稳定性和支承力得到提高（朱鸿鹄等，2022）。虽措施可以多种和复杂，但都可视作对隧道偏压段地表的软弱岩土体加筋加固，以提高围岩土体力学性能的措施，也即相当于岩土体内摩擦角（ϕ）、黏聚力（c）均取得一增量△ϕ、△c，且△ϕ、 △c＞0。以此，利用库伦和朗肯定律深入分析：假设平衡压重填土体作用于基准面的荷载为（Q）、侧向应力和达到塑性极限平衡状态的侧限被动土压力为（σ₃）、岩土体内摩擦角（ϕ）、黏聚力（c）；则塑性极限平衡状态的侧限被动土压力（σ₃），σ₃=Q×tg²（45°+ ϕ/2）+2c×tg（45°+ϕ/2），加固后，塑性极限平衡侧限剪切应力（σ_f），σ_f =Q×tg²[45°+（ϕ+△ϕ）/2]+2（c+△ c）×tg[45°+（ϕ+△ϕ）/2]；而式中Q×tg²（45°+ϕ/2）＞0，岩土黏聚力c因工程加固地表砂浆锚杆和铺设一层或多层的钢筋网水泥混凝土结构层得到一增量△c，所得c+△c参数比原来c值大幅度提高；又因正切三角函数在第一象限是增函数，且均为正值，故得σ₃+ △σ₃=σ_f ＞σ₃，即△σ₃＞0，因此，隧道偏压和浅埋段地表的软弱岩土体整体侧抗限剪应力大大加强提高，从而，相应提高隧道围岩的整体稳定性，提高了隧道施工和使用的安全性。

隧道偏压段采用的地表砂浆锚杆与钢筋网混凝土层加固处理，其作用等效于其围岩内摩擦角和黏聚力均取得一个较大的增量，其理论相当于隧道围岩系统锚杆加固围岩增强抗剪应力。由此可知，加固锚杆的力学作用，等效于软弱岩土体都有△ϕ、 △c的正增量。

由此可知，在趋于变形的建设工程中，假如充分运用加固措施的力学性能与岩土力学性能所具有的等效性，那么，处于失衡土体完全可转化为另一新的平衡状态，使围岩土体控制在一个新的极限平衡状态内，在新的平衡状态系统中保持永久性的稳定。

5.5 建设工程质量偏心现象加固机理

5.5.1 软基段桥台预压超载质量偏心现象加固机理

软基段桥台超载预压加载土层一般较高，而且与软基段路基同堆载预压；但两者填土量需求不同，桥台的预压土须较高，在桥台形成较高堆载体。一般来说，处于软土地基桥台堆载预压的层厚都要大于 10 m，如果需要超载预压者，则需要层厚大于 15 m以上，因此，超高路堤下的地基土将要受到0.3 MPa 土压力，而软土淤泥地基承载力一般为 0. 03 MPa 左右，这就是桥台超载形成的偏压现象。由于桥台预压超载土体造成偏压，存在偏心距，产生偏心力矩，故此引发周边地基土地拱，破坏已建建筑。

由此，采用水泥搅拌桩加固地基，并采用地下连续墙围护，围护结构与水泥搅拌桩形成一体复合地基，加强了搅拌桩的水平抗剪力，使整个复合地基稳固而不致于沉陷坍塌。其中，地下连续墙既可作为复合地基，也可切断因偏心矩产生的地基水平剪切力。地下连续墙是由5 m深的高干密度级配砂性填土和多层的土工格栅构成，其内部铺设多层的土工格栅，可使回填砂性土的内摩擦角ϕ₁和黏聚力 c₁形成一个相对较大正的增量（王家全等，2022），即得到较大的△c₁和△ϕ₁，从而提高回填土抗剪力（牛笑笛等，2021），按照试验段的采用十字板试验表明：平均可提高 0.13 MPa。由上述分析可知，加固结果剪切应力可用数理描述，其剪切应力表达式为：（σ_f1），σ_f1=Q₁×tg²[45°+（ϕ₁+△φ₁）/2]+2（c₁+△c₁）× tg[45°+（ϕ₁+△ϕ₁）/2]，从上式可知，σ_f1已经获得大幅度的正增量。

5.5.2 隧道偏压质量偏心现象加固机理

隧道工程中，因不对称压应力而出现偏压，在隧道洞身顶部，若存在偏压段则会形成的形体偏心土体。首先，由于形体偏心土体而存在偏心距，在围岩内外力共同作用下，而产生了矢量的偏心矩； 再次，因偏向力矩作用则可导致隧道工程遭破坏。

但是，通过地表砂浆锚杆或注浆小导管的加固、回填衡重的级配砂性土，因其每间隔一层铺设土工格栅，可使加固后的回填砂性土的内摩擦角 ϕ₂ 和黏聚力 c₂形成一个正的增量，即△c₂和△ϕ₂，从而提高回填土的抗剪力。按照试验段的采用十字板试验表明：平均可提高 0.10 MPa，侧限剪切应力 （σ_f2），σ_f2=Q₂×tg² [45°+（ϕ₂+△ϕ₂）/2]+2（c₂+△c₂）×tg [45°+（ϕ₂+△ϕ₂）/2]。

为验证隧道偏压质量偏心的加固效果，在博深高速的龙岗1^＃隧道的偏压段开挖施工中，进行深入研究偏压围岩段对隧道拱圈的应力动态，对应的初步设计标高对工程实体进行原位试验，采用盲孔应力检测法进行现场监控实测，以施工图隧道拱顶为中轴线，在中轴线两侧同一断面内拱肩内，各布置7 个竖向应力观测点，连续实测多个断面。两侧拱肩分向偏压面和背偏压面，在拱顶设置第一检测点，远离拱顶依次排序到第七点，点号为l _向和l _背。向偏压面 σl _向1=1336. 0 kPa、σl _向2=1372.1 kPa、σl _向3= 1391. 0 kPa、σl _向4=1322.5 kPa、σl _向5=1400.2 kPa、 σl _向6=1301.7 kPa、σl _向7=1333.5 kPa，背偏压面 σl _背1=819.7 kPa、σl _背2=859.8 kPa，σl _背3=799.7 kPa、 σl _背4=905.7 kPa、σl _背5=951.2 kPa、σl _背6=883.6 kPa、 σl _背7=892.8 kPa。而每个断面的向偏压面和背偏压面同一数位点 n 是对称的，在此以同一数位点作对比，求出其比例系数，ν＇_n=σl _向n/σl _背n，即 ν'₁=1.63、 ν'₂=1.60、ν'₃=1.73、ν'₄=1.50、ν'₅=1.54、ν'₆=1.47、ν'₇ =1.49，自上计算可知，隧道拱肩向偏压竖向应力明显消减，拱肩向偏压与背偏压比例系数大幅度降低，拱肩两端出现向平衡的趋势，工程质量偏心隐患大大减少。

在实际工程试验段连续共布置30个断面，形成网格，网格之间为步长，在连续空间形成数学矩阵。

5.5.3 建设工程质量偏心现象加固机理的微观分析

从微观角度看，不管是后填的改造土层，还是原生围岩，都是细微的岩土单元组成。在土层里，组成单位是土粒；在块状的岩石里，组成单位是矿物，但无论哪种组成，岩土层里的每个单元内总有组成单位的摩擦力和吸附力，而每个组成单位的摩擦力会叠加成总内摩擦力、每个组成单位的吸附力会叠加为总吸附力，总的摩擦力与吸附力分别以内摩擦角、黏聚力呈现，从而土单元可构成土粒，土粒则可通过内摩擦角和黏聚力合成力限制彼此相对移动。倘若每一土层间铺设土工格栅或竖向砂浆锚杆，即同样限制阻碍每层土粒作相对移动变形，也就是说土工格栅或竖向砂浆锚杆的加入提高了岩土体的内摩擦角和黏聚力。

在软基段桥台预压地下连续土围护墙里，因回填土经过密实，土粒的内摩擦角、黏聚力得到大幅度提升，因此通过加入土工格栅形成加筋土地下连续墙，加筋则对土粒限位效应更大。由原位测试结果可知，与铺设土工格栅前相比，加筋土的地下连续墙抗剪应力得到很大提高。由此，验证了如下数学式的理论正确性，经加固填土的剪切应力（σ_f1 ），σ_f1=Q₁×tg² [45°+（ϕ₁+△ϕ₁）/2]+2（c₁+△c₁）×tg[45°+ （ϕ₁+△ϕ₁）/2]。

在隧道偏压地表砂浆锚杆、填土分层间铺设土工格栅的衡重体系里，除了土工格栅对土粒限位效应外，还有砂浆锚杆和支挡结构挡土墙也可进一步提升回填土抗剪应力，更能提升回填土与原偏心偏压围岩的整体性，从而更大程度地提高隧道工程在偏压段、特别是在洞口浅埋偏压段的永久稳定性。同样地，由原位测试结果可知，经加固的回填土比未加筋加固时抗剪应力显著提高。因此，解释土体加固后的剪切应力（σ_f2），σ_f2=Q₂×tg²[45°+（ϕ₂+△ϕ₂）/ 2]+2（c₂+△c₂）×tg[45°+（ϕ₂+△ϕ₂）/2]数学式的理论正确性。

5.6 建设工程质量偏心的工程隐患治理力学机理

建设工程因质量偏心现象出现，导致产生标量偏心距，在岩土体系内外力的作用下，因而形成矢量偏心矩。由于岩土体系偏心矩形成，导致岩土力学体系超出极限平衡出现不平衡状态（章瑞环等， 2021），即产生不平衡因素，致使岩土体系存在工程质量安全隐患。

然而，岩土体系因质量偏心造成的工程隐患是可治理的。从以上工程案例可知，在岩土力学结构上，采用支挡限位、利用支挡力矩抵消因偏心产生的偏心矩。在桥台预压和隧道偏压的偏心现象已经阐明：桥台预压的偏心力矩可用搅拌桩加固地基土和地下加筋土的连续挡土墙，抵消因超高的预压土在软土地基所产生的水平剪应力，当然，因水平剪应力较大，地下加筋土连续墙的质量需较高、墙厚需较大；而隧道偏压偏心现象的治理则是采用地表砂浆锚杆、台背回填加筋土形成与偏压段围岩抗衡的容重，并且与偏压段成为一体，其中，因地表锚杆于竖向、加筋土于横向加固，致使工程体系水平抗剪应力得到大幅度提升，从诸多方面抵消了隧道偏压水平偏心矩。

其实，在软土地基的路基段，因同样需堆载预压，故存在偏心距和偏心矩，但路基填筑不像桥桩受工期过紧限制，可通过加密沉降观测、严格控制路基填筑速率，通过边坡反压护道反压限制，更重要的是路基的软基处理的排水板或袋装沙井或沙桩或粒料桩使孔隙水排出，使孔压稳定，不致于软土地基产生过大的水平剪应力，并且大大提高地基承载力；另者，采用 CFG 桩或搅拌桩或预制桩则大幅度提高软土地基的承载力，由预压路堤传递来的偏心矩在水平向上也得到限制抵消，可使路基坡脚不发生滑移坍塌，以达到限制路基工后沉降量，避免造成周边地拱。

5.7 建设工程质量偏心的工程隐患治理必要性

建设工程中，质量偏心现象在实际工程中是常见的，并且对建设工程存在不小的质量和使用安全隐患，而此类隐患是可治理的，也必须治理的。

隧道的岩土体出现偏压失衡现象，导致隧道结构稳定性和安全性受到威胁。实际工程中，必须采用工程技术手段消除因偏压所产生的偏心距的不利因素，也就是说：由于工程的偏压段造成偏心距的出现而导致偏心力矩的产生，由于偏心矩的产生导致隧道洞口和洞身潜伏隧道工程质量和使用安全的病害，致使隧道工程埋下安全隐患，所以，采取必要的技术和方法治理，才能保证隧道工程相对永久性的稳定与安全。

在如同软土地基的桥台超载预压实际工程中，采用填土加设土工格栅形成地下连续墙等措施，可大幅度提高土体抗剪应力，得到足够抗剪力抵消由于偏压带来的偏心矩，因此加固工程，从而消除由偏心力矩所产生的影响工程整体稳定性和安全性的因素。

其实，存在质量偏心现象的工程中，因其往往处于变化复杂的力学体系环境，致使偏心距变化值超出界定，偏心矩作用也超出安全控制范围，成为工程体系偏心病害，若不正确对待偏心距和处于复杂力学环境的偏心矩，必然造成极大后患。如未作出相应的措施治理，一旦土应力集中，将会造成建设工程整体失稳，造成建设工程地基或围岩或支挡结构大规模沉陷与坍塌。因此，针对建设工程偏心极可能导致偏心距超出维持岩土体稳定的必要条件，必须治理工程体系因偏心距超出界定而导致偏心矩失衡，致使工程坍塌的病害。

6 结语

因本文侧重研究建设中的工程岩土工程，在研究岩土工程中，侧重研究岩土工程质量偏心现象，而对于建设工程的刚度和强度偏心问题有待于其他领域再深入探讨。

在此说明：首先，在隧道工程中，虽以现场实测试验数据已在连续空间形成数学矩阵，并建立行列式方程，由于所建立函数方程在定义域区间连续，因此可建立微分方程求得拱顶空间任一点竖向土压应力的叠加量，但此仅是建立在理论探究。因未利用计算机使用数据模拟方法更精准地验证理论分析的可靠性，所以，有待采用有限元数学方法建立计算机程序，并深入地探索理论的科学性；其次，在陡峭岩土高斜边坡坡体，相对于原地面，也属于质量偏心的现象，在复杂地质条件下，高陡斜坡崩塌等地质灾害时有发生，崩塌稳定性计算及评价的精确度仍有待进一步深入探讨（付方华等，2023）。

综上所述，不管在软土地基桥台工程和隧道岩土工程，还是陡峭岩土高边坡中，常存在超限值的较大偏心，而出现质量偏心现象，从而产生了偏心距，在新建的力学体系作用下，因为偏心的存在，导致偏心矩的产生。偏心距在超出允许力学条件要求时，都会影响建设工程的整体稳定性，致使工程的质量和使用安全存在隐患，对于永久工程来说，因其危害性极大，正确认识、对待所有的建设工程的偏心距和偏心矩是十分必要的。

建设工程出现质量偏心，工程体系不稳定，可以是偏心矩或荷载至少已超出允许要求，造成应力局部集中所致，对于地基基础工程来说，导致支挡体系存在倾覆与坍塌的病害隐患，危害整体体系的稳定安全。而导致建设工程质量偏心的因素不论是内力还是外力，都存在随机性和频繁性，因而偏心现象随时威胁建设工程整体安全稳定性，而诸如此类的防护措施仍缺少实质性探究。

在实际工程中，建议如下两方面研究，首先，针对问题加大原位测试频数，加密观测点频率，对实测数据采用数理回归分析（李斌等，2022），准确推算相应的回归系数、建立实际工程所相对应的回归方程、印证本文所提出的加固土力学机理分析方程 （σf），σf=Q×tg2[45° +（ϕ+ △ ϕ）/2]+2（c+ △ c）×tg [45°+（ϕ+△ϕ）/2]成立；其次，因方程（σf），σf=Q×tg2 [45°+（ϕ+△ϕ）/2]+2（c+△c）×tg[45°+（ϕ+△ϕ）/2]中的加筋土两个增量值△ϕ、△c与加筋材料的纵横二维向伸长率ρ相关，且存在一个成反比例关系，即式中加筋土两个增量值△ϕ、△c，△ϕ=β/ρ、△c=γ/ρ，而β、γ分别为 β、γ两项不同的待定分项系数（张玲等， 2021），整理后成方程（σf），σf=Q×tg2[45°+（ϕ+β/ρ）/ 2]+2（c+γ/ρ）×tg[45°+（ϕ+△ϕ）/2]，其中σf矢量方向与ρ伸张方向同向。

此外，在破碎的岩质边坡工程中，经常采用锚杆、锚索加格构梁、桩板墙加固限位的措施，以此解决岩质边坡的质量偏心问题。采用锚索格构梁和桩板墙两者相结合的治理方式，对破碎性的岩质双滑面的滑坡的治理效果较好，既能对已发生位移的滑坡进行有效巩固，还能有效提高滑床在滑坡体初始运行阶段的抵抗能力。从而更充分证明了本文提出的加固土力学机理分析方程的正确性（岳庆等，2023）。

因此，在治理因存在偏心矩作用问题而潜伏病害隐患的建设工程中，要使建设工程长期处于安全稳定状态，除了要有可靠定性的理论依据外，还须建立定量的分析理论。仅有如此，因质量偏心存在的偏心距和偏心矩问题，以及由其所引发的建设工程安全隐患才能得到精准防护和深入研究。

参考文献