0 引言

固体矿产资源储量估算是矿产勘查和矿产资源管理的关键环节，也是实施数字矿产战略的重要技术。在矿产的逐步开采过程中，由于固体矿产资源储量的减少和勘探方法等因素，矿体的储量总是处于不断变化的状态。因此，矿体储量估算是一项相对复杂的系统工程，准确估算矿产储量可以为合理制定矿体开采程序和方法提供参考价值（宋彦东等，2023）。

目前，广泛使用的矿产资源储量估算方法包括克里格法和垂线法。克里格法以统计指标作为估值准确性的不确定性指标，以原始样本数据为基础，根据估值的优点分析研究矿区矿体的基础数据，进而估计矿体储量。但该方法受矿体品位和体积的影响较大，对于动态变化范围较大的矿产资源，其估计误差较大；垂线法根据矿层厚度和向下运动角度计算矿物边界的覆盖程度，并结合矿体的空间形态和矿化强度的可变性估计矿产资源储量。然而，这种方法缺乏对估计结果的不确定性描述，并且忽略了矿石品位分形的影响，因此估计结果与实际结果之间存在显著偏差。

鉴于以上分析，本文以平行断面法为技术支持，提出一种固体矿产储量估算方法，通过矿体边界圈定、矿体体积计算，估算出研究区内矿产储量值。

1 固体矿产储量估算方法设计

1.1 矿体边界圈定

单工程矿体圈定可将矿区内矿体的分布情况展现出来，为后续矿产储量估算奠定基础。矿体边界圈定是根据地下矿床的矿体平均品位与开采厚度对矿体和周边围岩进行划分，并对单个勘查项目中的超高品位矿体进行厚度调整与处理（王刚和魏文强，2023）。

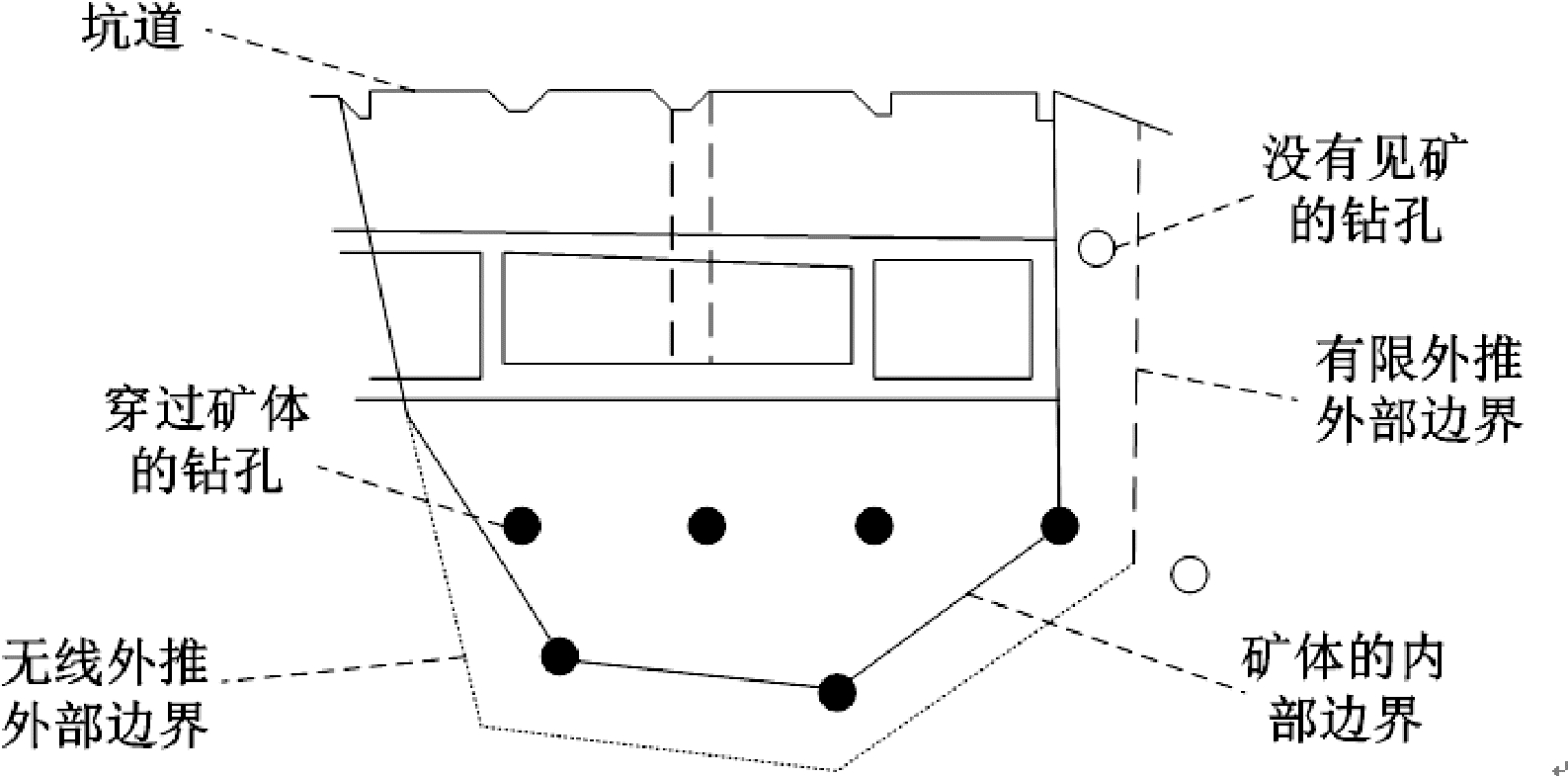
本文采用阵面推进法将矿体边界用网格的形式来表示，根据图形数据结构，提取目标区的所有约束边界，从而生成矿体的四面体网格边界。矿体圈定剖面图如图1所示。

当矿体与围岩的边界线相对清晰，可以利用自然勘查工程对剖面进行直接观测和测量来确定（张与伦，2023）；当矿体与围岩的边界相对模糊且呈现渐变关系时，则需要根据目前的工业指标，采用前沿推进法确定矿体边界的基点位置。

首先，将地下矿床抽象为空间连续的品位数据场，将穿过矿体但没有看到矿石的钻孔数据作为原始钻孔数据集，记作 P{ p₁，p₂，. . .，p_n}。由于多金属矿床本身的品位值不符合正态分布，为了简化计算过程，准确估计矿产资源量，有必要对原始数据集进行对数处理，使其符合标准状态分布（岳鹏军等， 2021）。计算公式为：

式（1）中，Y（u）表示矿体区域化变量；ΔZ 矿体品位变化最大值；a表示变换系数。

假设对数变换后的数据区域，未知点位置的数据也遵循高斯分布，则原始数据的条件概率分布函数可以表示为：

式（2）中，G表示高斯函数；ϕ（z）表示分位函数； G'表示高斯函数的逆函数；f_p 表示原始数据的条件概率分布函数。

对该集合中的所有数据对象进行三角变换，变换公式如下：

式（3）中，p'_i 表示新点集；C_i表示协方差；p_i表示第i个原始钻孔数据；Z_i表示方差。

经过上述对原始数据的变换处理，结合计算机程序对矿体边界进行圈定，具体步骤如下：

将新点集中由水平点、数值点和相应原始数据点组成的简单截面 F 添加到新点集 P'中的外部点集，并选择 F面的外部点集中最远点 F₀与每个点集中非空面的连接面作为可见面集（王永亮，2022）； 创建一个由 F₀与相邻面 V组成的新面，将新面连接到截面 F，并删除 V 中的所有脊面；在这一点上，获得了新点集P'的凸边界；再从凸边界去除一维数据之后，可以获得原点集的三维网格数据。依次连接网格数据点，生成地下矿体边界（赵辉军等，2022）。

利用上述方法，矿体所有的线边界均已出现在四面体网格中，即完成固体矿产的边界圈定。便于接下来计算边界内的矿体体积。

1.2 基于平行断面法的矿体块段体积计算

平行断面法的特点是可以根据矿体边界剖面所代表的矿体的产状、结构和不同性质来研究矿体块体的分布（王玉祥等，2022）。

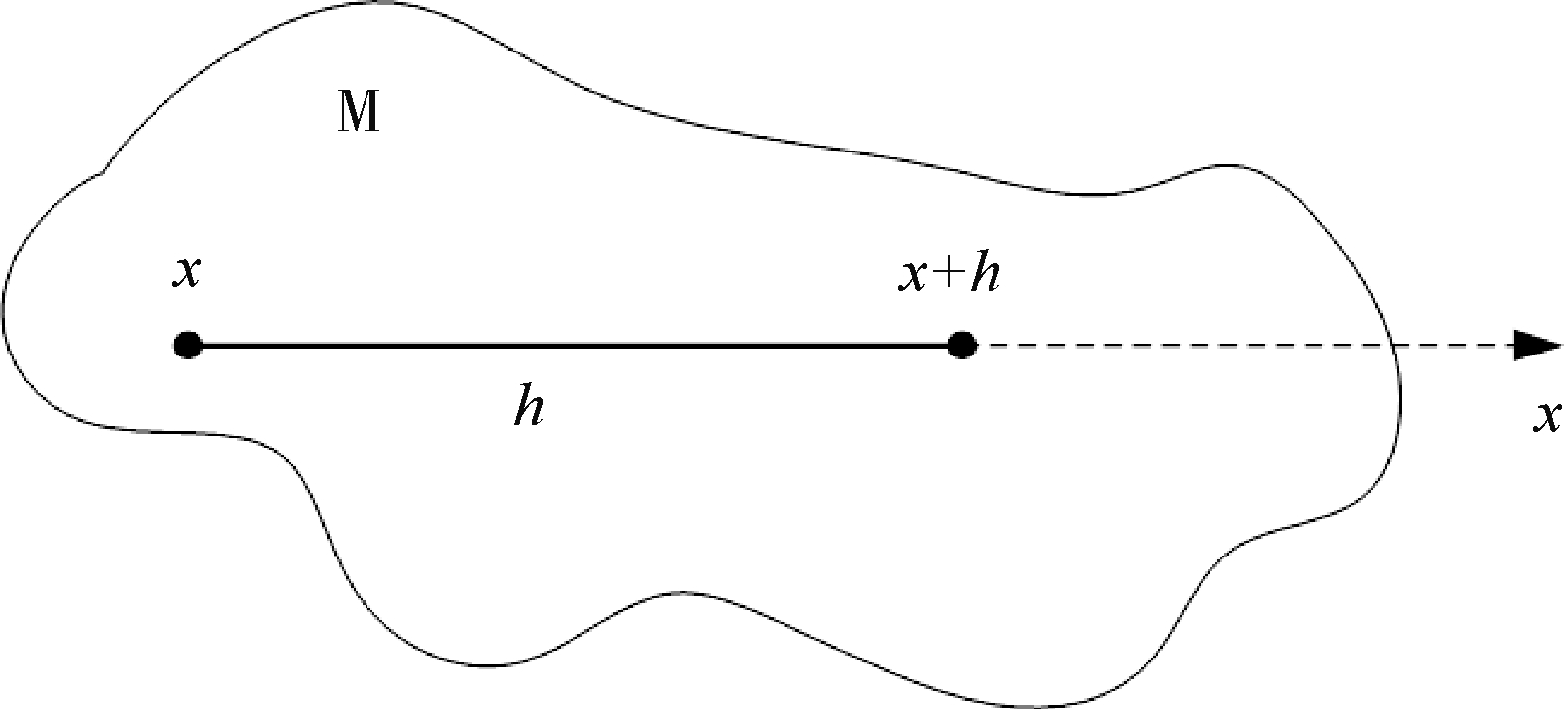
将矿石带视为空间中的一个区域 M，该区域中的所有值都可以视为该区域内从一个点到另一个点的可变值，如图2所示。

沿矿带区域x方向将域内分割为若干个具有相同矢量 h的对点时，即可得到两个对应观测值 Z（x）与 Z（x + h），则两者差值平方的期望可用变异函数表示：

矿产资源的分布属于具有地质意义的构造信息，因此可以将矿体的体积视为一个变量。然而，在实践中，矿体样本的数量是有限的（戴家铖和邓飞，2022）。因此，实验变化函数是通过对由有限的测量样本值组成的变化函数进行属性转换而获得的，记为α（h） ^*：

式（5）中，N（ x）表示区域化变量值的增量方差。嵌套结构中的每个实验变异函数都代表了矿体在特定尺度上的变异性。在定量描述矿床特征时，根据矿床的变化结构，使用以下公式推断出矿床的理论分布：

式（6）中，a₀表示矿带区域变程；A₀表示矿层与岩层的交互现象；α₀（ h）表示矿带的范围。

在计算矿体块体的体积时，还应考虑矿化的性质。当矿化现象在各个方向上具有相同的特征时，它是各向同性的，反之亦然，均表现在 α₀（ h）的不同方向上的差异（蔡家驭等，2022）。不同方向上矿化可变性的差异可以表示为：

式（7）中，k_v表示矿体偏度；a₁表示变异系数；β₀ 表示矿体峰度。

对于任一待计算体积的矿体块段，矿体的平均品位估计值的计算公式为：

式（8）中，h 表示矢量值；n 表示矢量对点个数； λ_h表示加权因子；y_h表示无偏估计值。

在给定的待计算区块 M 和一组待计算信息 {y_h，h = 1，2，. . .，n}中，如果估计的方差最小化，则可以在尽可能小的质心间隔内生成区块 M 的计算值（朱梦菡和王昭，2022），进而得到用于获得矿体品位的替代阈值为：

式（9）中，GL表示替代特高品位矿体的阈值；σ₀ 表示特异值；m表示矿体特高品位临界值，其计算公式为：

式（10）中，μ₀ 表示拉格朗日常数；γ 表示诸权系数。

为了抵消相邻两段矿体的形状和相对面积差异，以及矿体夹出位置的形状对矿体块体体积计算结果的影响，引入矿体计算点的权重，对体积进行演化和估算（袁姝和刘粱金，2022）。计算公式为：

式（11）中，h_w 表示垂直矿层方向的变异性；η_x表示矿层尖灭距离；z^* 表示矿体平均品位。

最终得到计算矿体块段体积V的公式为：

式（12）中，L表示相邻剖面间距；S₁、S₂分别表示相邻剖面对应矿层面积；R表示指示阈值。

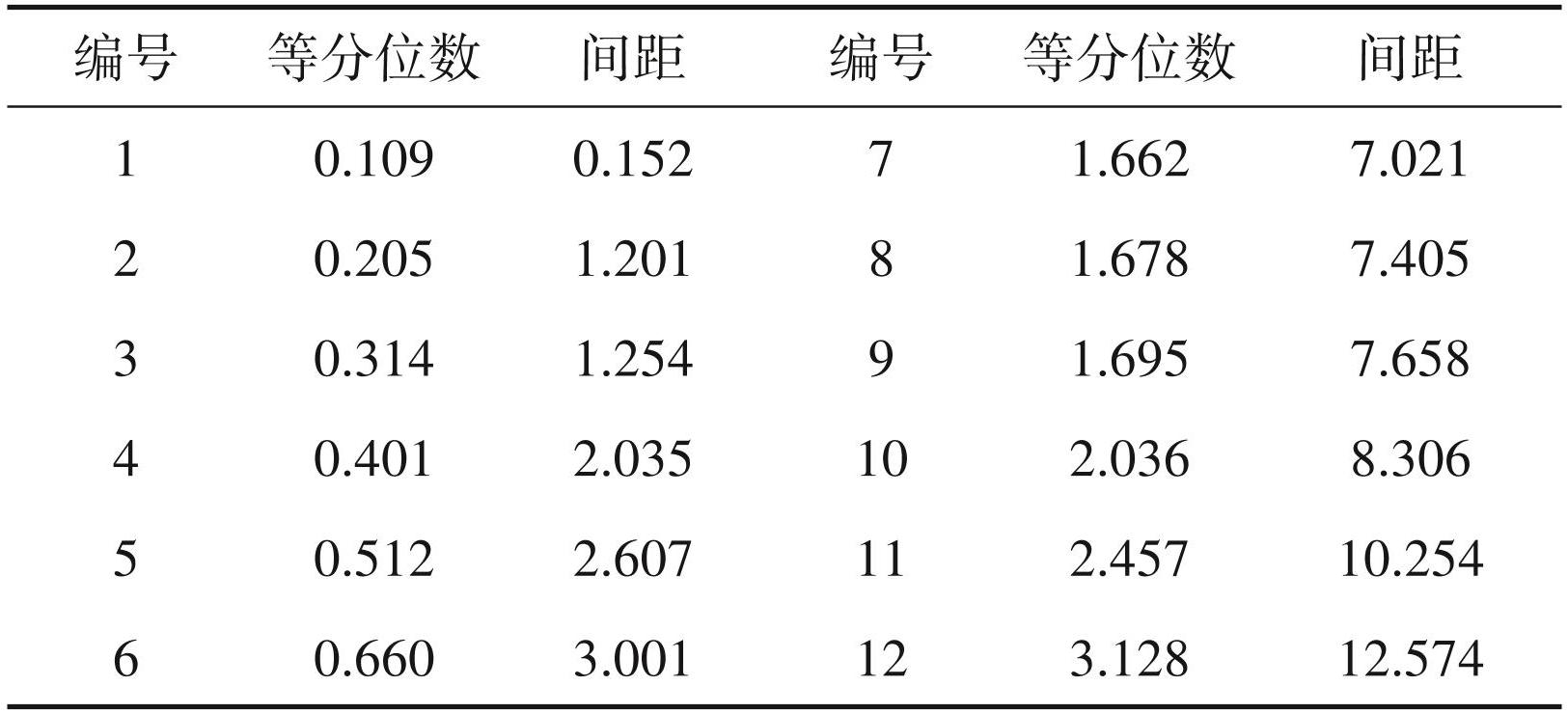
根据计算需要，指示阈值 R 的选取通常由矿体的等分位数与相邻间距决定（刘金刚等，2020），根据此种方式设定的12个指示阈值如表1所示。

根据矿体边界圈定范围内矿体的几何形状、构造与质量，将矿带区域划分为多个具有矢量对点的观测值，结合矿体在空间尺度方向上的特异性，估算矿体的平均品位，并推导矿体地理分布，继而通过合理选取矿体特高品位的指示阈值计算出矿体块段的体积。为估算矿产资源的储量提供了便利条件。

1.3 固体矿产储量估算

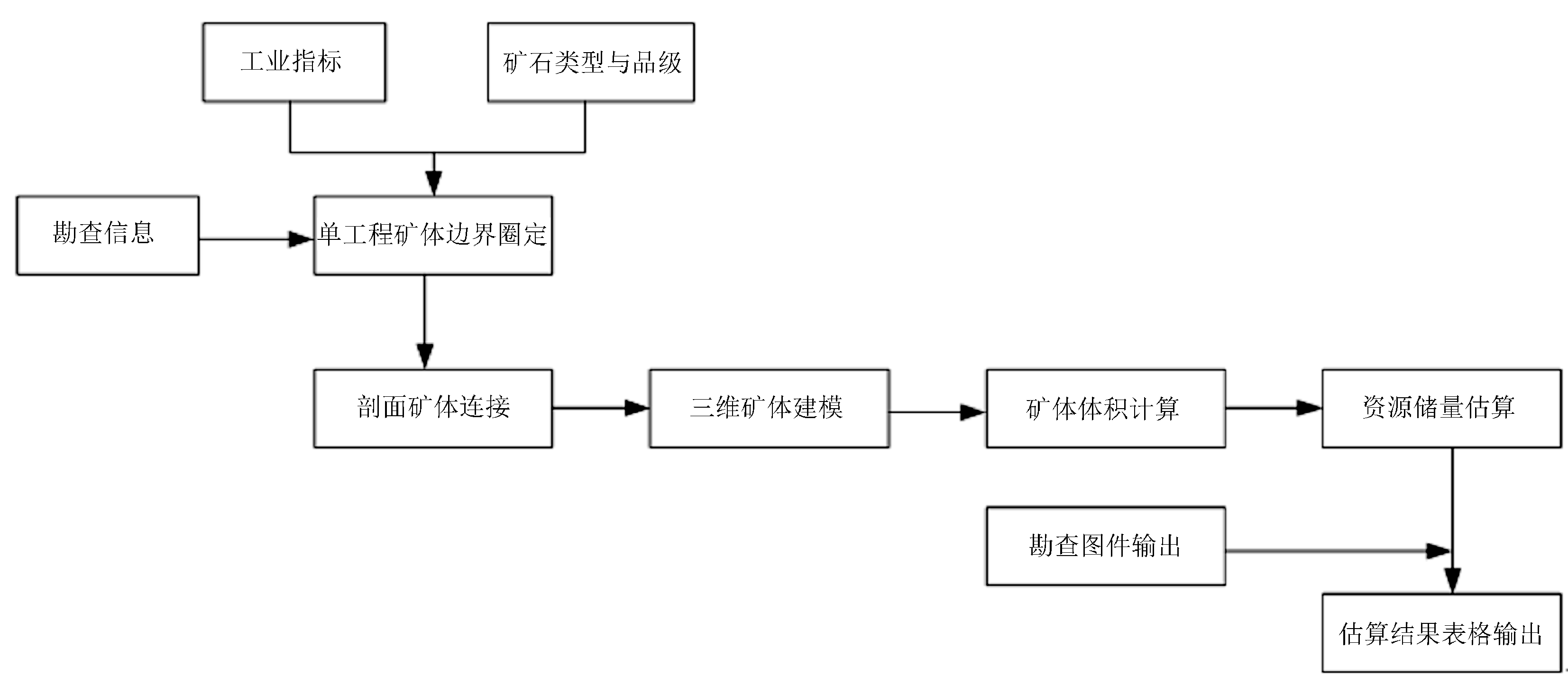
根据矿体块体的体积计算结果，根据勘察工程获得的信息，科学地估计矿床的质量、伴生元素的分布、金属含量和储量，以明确目标区域的矿产资源分布（乔淇等，2020）。固体矿产资源储量估算过程如图3所示。

将勘查所取矿体的所有边界断面置于三维空间中，根据矿体的延伸趋势，利用轮廓拟合技术将相邻的勘查线用三角形网络连接起来，形成三维矿体表面。随机选择一个矿体边界，从边界的一角向三维矿体表面方向画一条垂直线（刘文凯和张雄天，2022）。其长度由以下公式表示：

式（13）中，H_P 表示矿层埋深；h_p 表示松散层厚度；c表示围护带宽度；β'表示矿层与水平线夹角。

将设计的线路工程坐标投影到矿层储量估算平面上，在工程外侧围护带 10~20 m 处计算各剖面矿层的移动角，即：

式（14）中，θ 表示走向方向岩层移动角；V 表示矿体体积；g表示矿体密度。

矿体密度的计算公式为：

式（15）中，（ x₁，y₁，z₁）、（ x₂，y₂，z₂）、（ x₃，y₃，z₃）、（ x₄，y₄，z₄）分别表示矿体模型的4个顶点指标。

假设围护带边界与矿层走向之间的夹角 ΔB在矿区中随矿层倾角的变化而变化，则根据矿层移动角可计算出区域化变量的全部协方差的平均值（马艳平等，2019），即：

式（16）中，ΔA表示分隔矢量的变化量。

为便于计算，将矿体组合样品进行正态变换，得到沿矿体垂直方向的松散层压覆体积为（董泽宝，2022）：

式（17）中，ω表示岩层上山斜交剖面的移动角。

将最小方差作为矿产资源储量的估算限制条件，以消除指示阈值对结果的影响（孙远强等， 2022），计算公式如下：

式（18）中，d_u表示估算最小方差；f_u表示品位值小于阈值的累积概率；Cov（.）表示换阶函数。

由此得到研究区内固体矿产资源储量的估算公式为：

式（19）中，Q表示矿产储量；S表示块段面积；H 表示块段平均厚度；R表示块段平均体重。

依据对矿区的勘查资料，计算三维矿体表面的垂线长度与矿层移动角，设置最小方差为储量估算限制条件，结合区域化变量协方差，求取研究区域固体矿产储量（李海泉，2021）。至此，完成基于平行断面法的固体矿产资源储量的估算过程。

2 实验论证

为验证文中设计的方法在矿产资源储量估算应用中的可行性，以实际矿区为研究背景，测试该方法的应用性能。

2.1 研究区概况

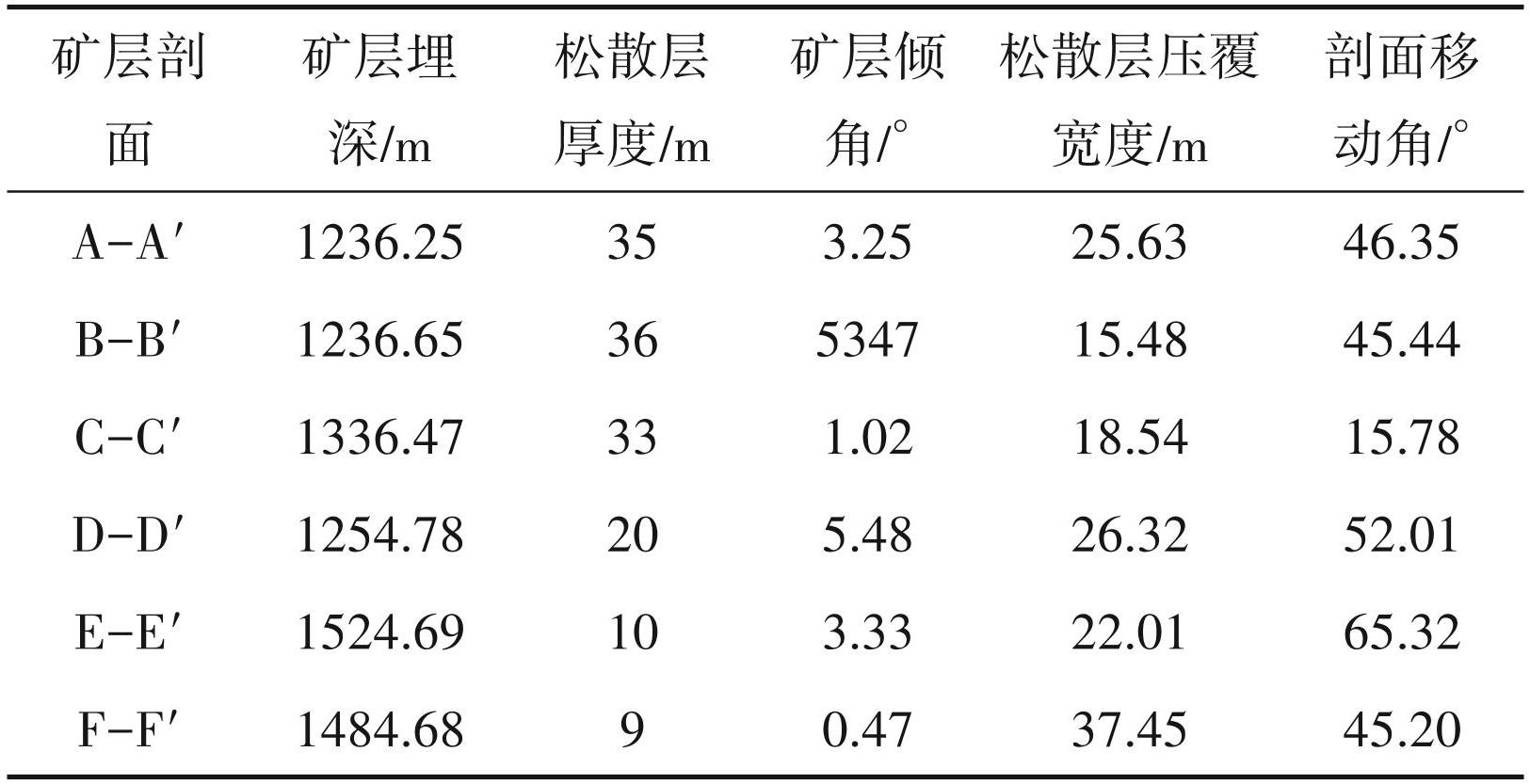
矿区出露地层主要为三叠系并伴有酸性岩出露；区域岩浆活动较强，矿化带主要分布在东北— 西南方向；整个矿化带全长约 1.65 km，矿化层的连续性较强；工程框架品位为1. 00%～1.56%，平均品位为 1.26%；矿区矿体呈平面状，长约 1256 m，南北宽分别为 453 m 和 457 m；矿体规模一般，形态相对简单；矿层最大厚度 20.45 m，平均厚度 5.32 m，矿体重量2~3 t·m^-3。矿区固体矿物剖面特征见表2。

本研究从矿区选取 162 个工程钻孔数据，包括矿体厚度（m）和平均矿体品位（%）。根据相关规定，以最小工业品位Ni ≥ 1%为工业开采厚度，以最小厚度为≥ 1 m 作为工业采矿厚度。因此，在采矿项目中，有 41个工业采矿项目和 114个低品位采矿项目。根据工程布局的原则和质量，划定了 102 类和123类资源储量水平范围。

2.2 实验准备

在实验中，使用采矿软件 DIMINE，采用平行剖面法估算矿产资源储量。首先，将钻孔等勘探地质数据按照线性关系有机地组合起来，表示钻孔的完整信息；其次，将其保存为 CSV 文件、孔径文件、倾角文件和矿体样本文件；最后，将这些文件导入 DIMINE 进行合并处理，作为建立地质调查数据的源数据，并更正缺失、不正确或重复的信息。将钻孔数据投影到每个剖面上，并根据钻孔走向、倾角和厚度的变化范围，或矿石类型和分布，使用文中描述的方法划定矿体边界线，如图4所示。

在划定的矿体中添加字段，并根据每个矿体的性质为这些字段赋值（官荣柱，2021）。

2.3 实验说明

该矿区样品的采样长度集中在 0.5~1.8 m。根据原始采样长度最小分割的原则，选择 1.2 m 的样品长度作为样品的组合分割长度。单个矿体内的样品数据之间存在一定的相关性，一般认为矿体内样品与矿体外样品之间不存在相关性。因此，在估算矿区内的储量时，只应使用矿体内的样本数据。通过样本组合和矿体边界约束，共得到矿体组合 I 的样本数量为1205个，最小样本值为0.2%，最大样本值为 11.254%，平均值为 1.48%，中值为 2.51%，方差为 1.204，变异系数为 0.652，偏度为 0.457，峰度为3.255。

2.4 矿产储量估算结果分析

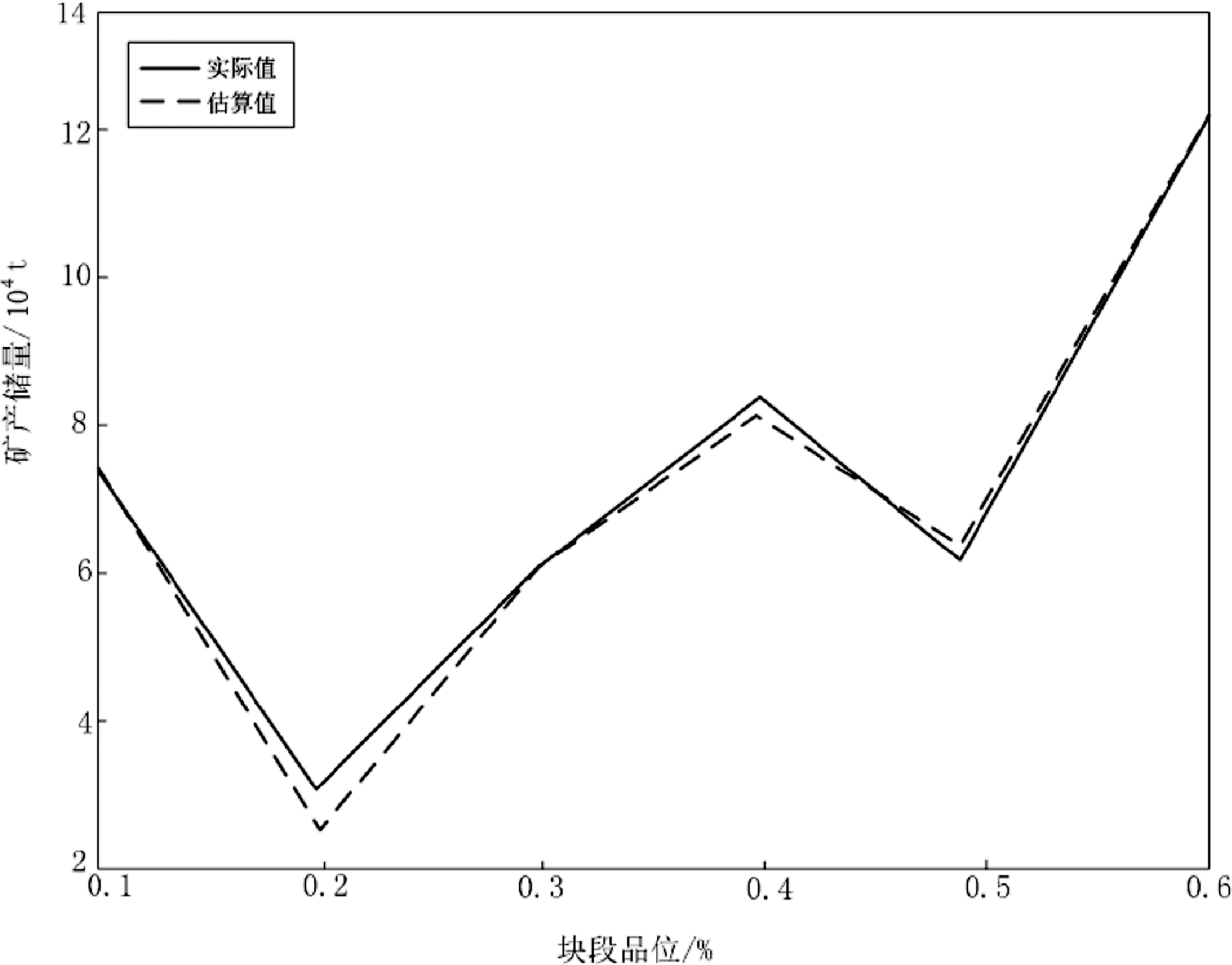
在实验中，设置矿体元素单元和字段等相关参数后，根据区块的平均品位计算矿体体积，并结合矿体边界划定结果，利用文中提出的平行断面法求取矿区内固体矿产储量，并与实际结果相比较，以评估设计方法的估算性能。结果如图5所示。其中采用密度仪对矿体进行实测和量化，得出矿产储量实际值。

分析图5 可知，应用本文所提方法对研究区内固体矿产资源储量进行估算，得到的估算值与实际值相一致，其中，准确估算出了块段品位为 0.1%、 0.3% 和 0.6% 条件下的固体矿产资源储量，且估算最大误差不超过 0.5。由此可见，本文设计的矿产储量估算方法具有较高的估算准确度。

2.5 估算准确性对比实验分析

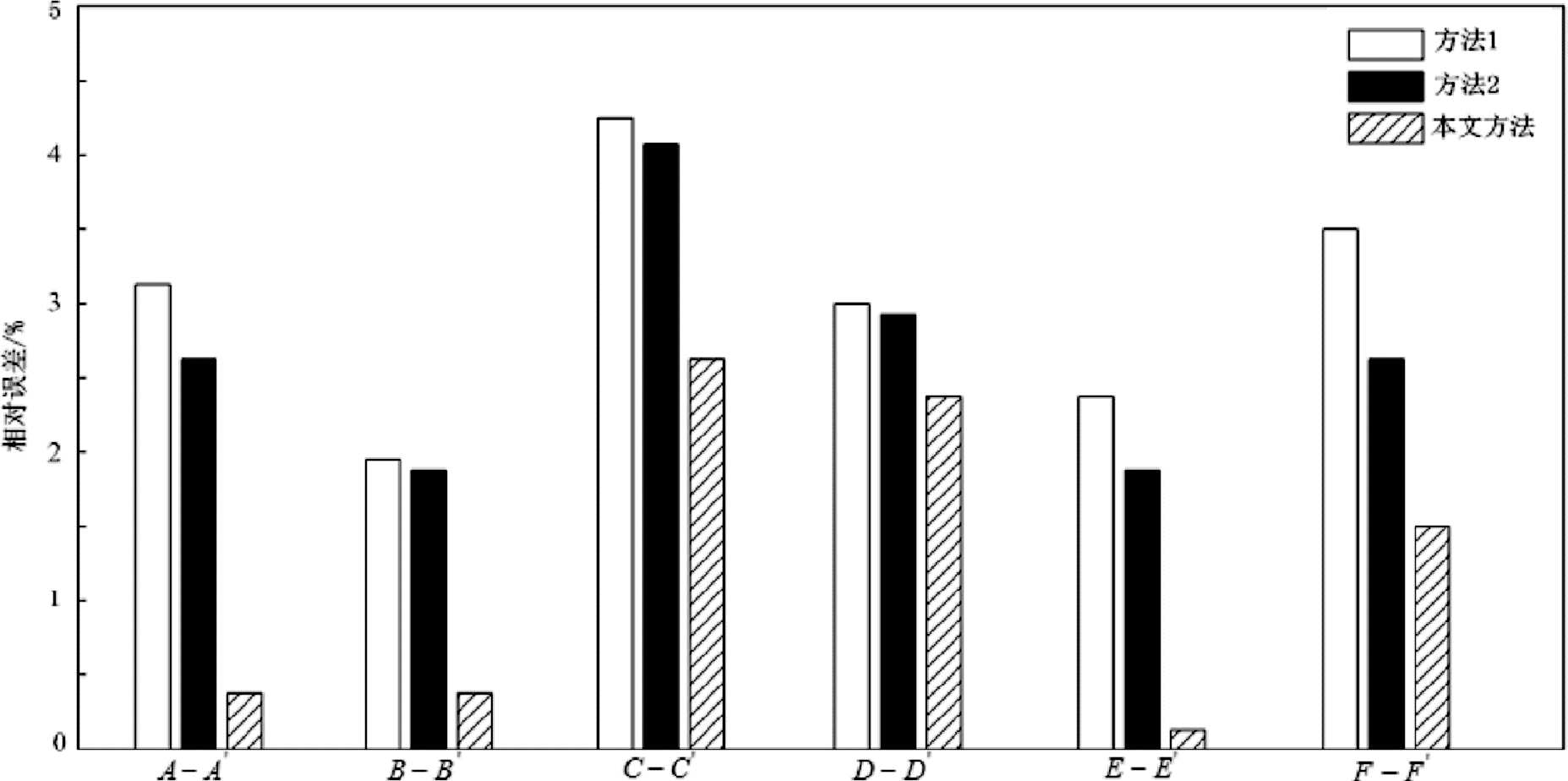
为进一步验证本文方法在矿产储量方面的估算优越性，采用克里格法（方法1）和垂线法（方法2）与本文方法进行对比，分别使用以上三种方法对矿区内 6 个矿层剖面的矿产储量进行估算，将估算结果与实际储量相比较，统计不同方法的估算相对误差，结果如图6所示。

从图6 可明显看出，对于不同矿层剖面的矿产储量进行估算，以矿层剖面 A-A'为例，方法 1 估算相对误差为3.1%，方法2估算相对误差为2.6%，本文方法估算相对误差仅为 0.4%，本文方法较其他两种方法降低了 2.7%、2.2%；方法 1估算准确性较低的原因是，该方法在进行矿体品位模拟时使用二项插值作为矿体体积的指示阈值，忽略了指示阈值具有动态变化特性；方法 2较优于方法 1，但总体估算效果仍然不佳，主要是由于其在划分压覆块段时，未将块段平面积考虑进去，故最终估算结果与实际值存在较大偏差。通过比较可知，本文方法能够提高固体矿产储量估算的准确度，估算结果更具可靠性

3 结论

利用平行断面法进行固体矿产储量的估算，可实现两相邻剖面间任意块段大小的矿产资源储量计算。经对比实验结果表明，基于平行断面法的矿产储量估算具有更高的估算准确性。该方法可作为矿产合理开采与生产进度策略制定的依据。

断面法是一种常用于固体矿产储量估算的方法，其基本思路是通过断面实测数据，推算出矿体的几何参数，然后采用正确的计算公式计算矿体的横截面积和体积，再进一步推算出矿体的储量。其优点主要包括：

（1）测量数据容易获取：采用断面法计算矿物储量时，测量数据较为简单和易于获取，只需要利用地质钻孔、隧道、巷道等工程断面实测数据进行分析和计算，在实际应用中具有一定的可操作性和实用性。

（2）计算过程简单快捷：断面法的计算过程相对简单，只需要利用相应的公式推算出矿体的几何参数和体积，进而计算出矿物储量。在软件和计算机辅助计算等技术的支持下，可以快速实现储量估算的工作。

（3）节省成本：断面法所需的数据比较简单，不需要消耗大量的时间和资金去实施大规模勘探和开挖，因此可以节省大量勘查成本。

缺点包括：

（1）示差大：断面法估算得出的数据可能与矿床实际储量存在一定误差，因为矿床的形态、尺寸、厚度和特殊条件等复杂因素会对结果产生一定的影响。

（2）适用范围较窄：断面法需要有完整的断面实测数据作为基础，适用于固体矿物床、薄煤层和柱状煤矿等，但对于难以测量的储量、扇形矿体和较大的煤层等复杂矿体类型，会受到限制。

综合来看，断面法对于某些固体矿产储量的评估仍然具有一定的重要性和可行性，但在实际应用中，需要充分考虑其优缺点，结合不同的矿床类型、勘查数据和评估需求选择合适的方法和工具，以保证储量评估的准确性和可靠性。

参考文献