0 引言

目前自然界中的土体，大多处于非饱和状态，不仅限于干旱或半干旱区域，即便土体层靠近河流也可能呈现出非饱和状态（王梓等，2021；钱建固和林志强，2023）。这种情况下，很多工程项目的施工都可能会碰到非饱和土体。由于该土体会严重危害工程，人们开始不断重视对土体抗剪强度的研究。本研究选定湖北省咸宁市通城县某一土体区域为研究区，该区域坐标位置为 113°46′26″E、29° 12′39″N。据前人研究报道，该地区非饱和土体内部存在很多微孔隙、微裂隙（叶云雪等，2022；刘才伟和赵丹凝，2023；张一豪，2023），当土体内部出现水的往返作用后，土体内部结构会出现不均匀性胀缩性，使得土体内部出现复杂的不连续面，引起土体抗剪强度降低。为了更好地抑制土体变形和土体破坏，需要提出合理的方法对土体抗剪强度衰减情况进行准确预测。

基于不同 PSO-ELM 模型的碾压黏土抗剪强度预测方法，金坎辉等（2022）为满足抗剪强度预测要求，设计包含激活函数的极限学习机预测模型，并引入粒子群算法对模型进行优化，通过优化后的模型得出抗剪强度最优预测结果。实践结果表明，该方法预测行为需要大量数据的支撑，使得预测方法应用局限性较大。矿渣微粉改良黄土力学性能及抗剪强度预测模型（杨国辉等，2023）以不同掺量配置的土体为研究对象，提出针对其开展无侧限抗压强度测试和湿陷性试验，根据实验数据了解土体机理，构建对应的抗剪强度预测模型。但是，该方法预测结果相对误差较大。酸雨环境下低矮 RC剪力墙抗震性能试验研究与抗剪强度预测方法（郑山锁等，2023），在人工气候实验室中，对土体抗震性能变化规律进行模拟，并在模拟过程中进行模拟静力加载试验，观察不同模拟参数下土体的变形情况，了解土体抗剪强度衰减规律，基于此得出抗剪强度衰减预测结果。试验结果表明，该方法进行抗剪强度衰减预测耗时较长。

考虑到以上几种研究方法无法准确预测土体抗剪强度衰减情况，为了有效解决这一问题，本文提出基于非饱和渗流特征模拟的土体抗剪强度衰减预测方法，以非饱和渗流特征模拟为核心，进行准确的抗剪强度预测。该方法通过有限元模拟分析模型，提取土体的非饱和渗流特征，并绘制土-水特征曲线，基于此计算出最优抗剪强度预测结果。实验结果表明，所提方法能够准确地预测土体抗剪强度衰减情况。

1 非饱和渗流特征的土体抗剪强度衰减预测方法

1.1 构建非饱和渗流数学模型

非饱和土是指土壤孔隙中既有空气又有水分存在的土体，这种状态下的土体性质与完全饱和或完全干燥的土体有显著不同。构建非饱和渗流数学模型，以分析非饱和土体中的水分分布和运动对土体的力学性质有着显著的影响，其非饱和渗流原理为：土壤的非饱和渗流原理是指在土壤中存在空气和水分的情况下，水分在土壤孔隙中流动的过程。在非饱和状态下，土壤孔隙并非完全被水填充，而是部分被水和部分被空气占据。这种状态下，水分的流动受到土壤孔隙结构、水分含量、土壤颗粒大小和形状以及土壤中空气压力的影响。非饱和渗流遵循达西定律的修正版，即非饱和渗透定律，其中渗透率是土壤水分含量的函数，随着土壤含水量的减少而降低。

以水体质量守恒方程为基础，针对目标土体，建立非饱和渗流控制方程，其表达式为：

式（1）中，A 表示容水度（%），c 表示压力水头 （Pa），B表示饱和度（%），S表示单位贮存量（m³），W 表示水的容重（kg/m³），v表示非饱和渗流特征系数。

式（1）中涉及的非饱和渗流特征系数是用来表示非饱和渗流规律的，可以通过 Darcy（达西）定律求出具体值（赵煜鑫等，2022）。

式（2）中，k表示土体的相对渗透率，K表示饱和渗透张量（Pa·s），α表示总水头（Pa）。

确定非饱和渗流控制方程后，为了更加准确地体现土体区域内渗流场具体分布情况，定义水头、流量、第三类边界条件（李嘉薏等，2022），得到优化后的非饱和渗流数学模型。其中，水头边界条件 c（t）的数学表达式为：

式（3）中，t表示时间（s），$\stackrel{-}{c}$表示已知水头（Pa），φ 表示水头边界上存在的已知水头数量。

为了规范非饱和渗流过程中的流量范围，将流量边界o_d表示为公式（4）：

式（4）中，o 表示流量（m³/s），$\stackrel{-}{o}$表示边界上的已知流量（m³/s），d表示单位外法线向量。

最后，针对饱和溢出边界和降雨蒸发边界形式进行分析，形成第三类边界条件。

式（5）中，δ 表示指示变量，c′表示水头极值 （Pa），o_d′表示流量极值（m³/s），T表示第三类边界，T₁ 表示饱和溢出边界，T₂ 表示蒸发边界，T₃ 表示降雨入渗边界。

结合式（3~5）所示的边界约束条件，构建非饱和渗流数学模型，作为后续非饱和渗流特征模拟的基础。

1.2 建立非饱和渗流特征有限元模拟方案

采用空间域离散策略和时间域差分原理（刘维明等，2023），对非饱和渗流控制方程处理，具体步骤如下：

（1）在数值计算中，一般采用数值方法对方程进行求解，而对于复杂的非饱和渗流控制方程，很难计算结果，因此需要将其离散化，转化为离散问题，以便使用计算机进行求解。

（2）时间域差分法是一种常见的求解控制方程的方法，将时间轴上的连续问题离散化为一个个时间步，通过迭代求解每个时间步上的问题，最终得到整个时间段的解。因此，将离散方程组转化为时间步进的形式可以方便地使用时间域差分法进行求解。

（3）空间域离散策略是指将空间上的连续问题离散化为一个个单元，然后在每个单元内利用有限元方法进行求解（郭涛等，2021；韩超等，2022）。有限元方法是将土体区域划分为若干个小单元，在每个单元内构建数学模型，用数值计算方法进行求解。

基于以上步骤，设置水头作为未知量，得到可以表达土体非饱和渗流特征变化情况的有限元计算模式（徐广泽等，2023；蒋胜波等，2021）。

式（6）中，∆t表示时间步长，I表示积分常数，i表示时间步。

其中：

式（7~8）中，λ 表示几何矩阵，N 表示形函数矩阵，均属于有限元模型中的关键参数。

基于上述计算公式建立的有限元模拟模型，是以网格的形式存在的。非饱和渗流特征模拟过程中（李叶鑫等，2022），考虑到土层分界面中压力水头不是保持不变的，为了更加准确地表现非饱和渗流特征，需要加密有限元模型的网格（郑威威等， 2022）。因此，提出以 Chebyshev（契比雪夫）网格法为基础，对有限元非饱和渗流特征模拟模型的均匀网格进行优化。均匀网格和 Chebyshev 网格示意图如图1 所示，实际操作过程中，网格点位置可以表示为：

式（9）中，j 表示网格点编号，η 表示网格点位置，L表示土体层厚度（m）。

如图1a所示，最初有限元模型中的网格属于均匀分布状态，相邻网格之间的距离完全相等，而经过 Chebyshev 网格法进行加密处理后（Nguyen et al.，2021；Xu et al.，2022），网格之间的距离发生改变，使得界面处网格节点发生高度加密（图1b）。此时，有限元网格间的离散格式可以表示为公式（10）。

式（10）中，z表示去除目标节点后，前后两个网格点之间的不等间距，Δz 表示 Chebyshev 网格节点间的不等间距（m），m 表示时间节点数量（个），ψ 表示水力传导系数，h表示网格列向量。

考虑到具有互补性能的第三类边界存在明显的非线性特征，使得非饱和渗流特征求解难度较大。在非饱和渗流特征有限元模拟方案建立过程中，引入抛物线型变分不等式方法，将互补边界条件看作自然条件，便于求解有限元模拟数值。

1.3 绘制土体土-水特征曲线

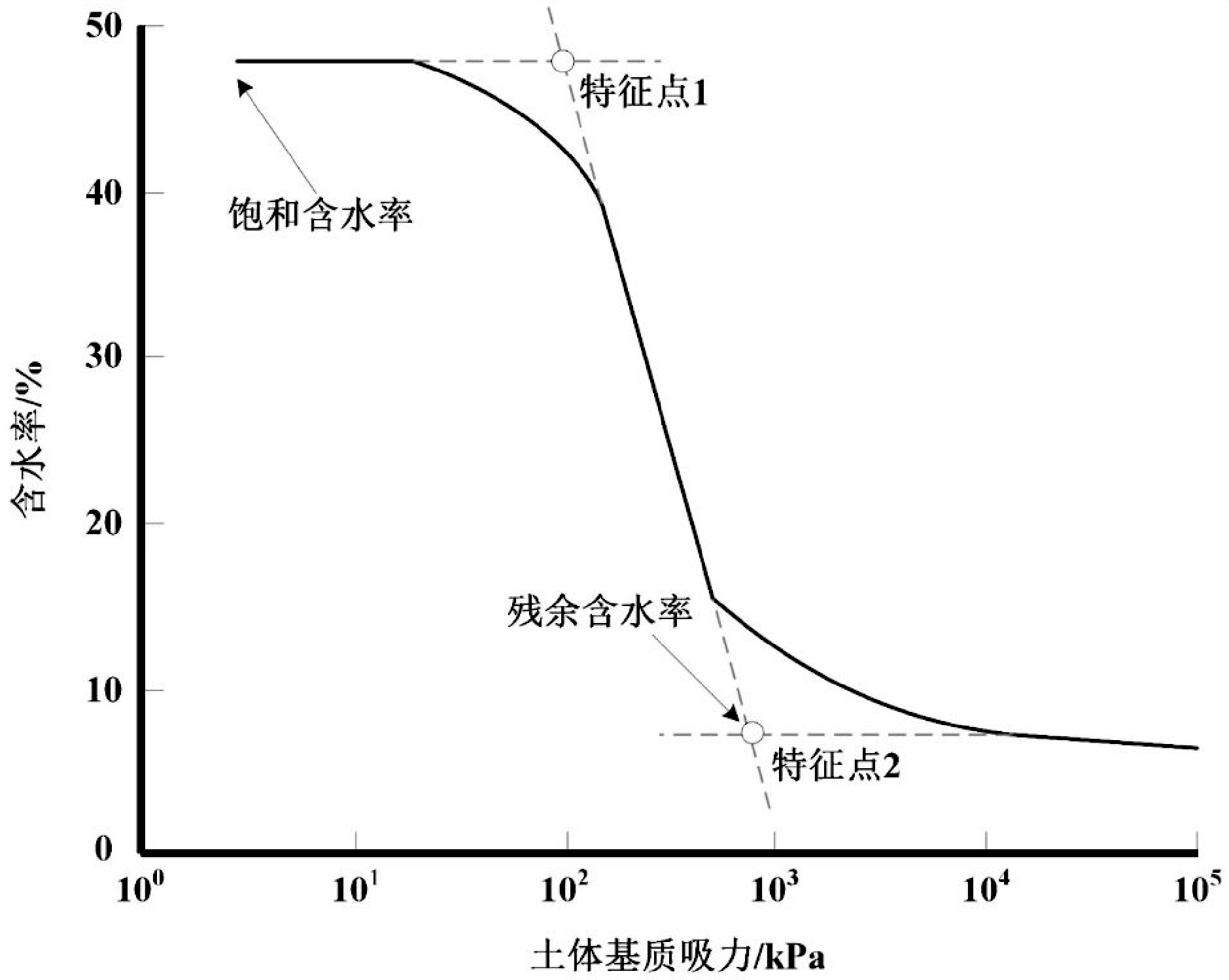
依托于有限元模型模拟非饱和渗流特征，可以基于此绘制出土体土-水特征曲线，通过该曲线可以体现含水率与吸力之间的联系。土体的土-水特征曲线是由脱湿曲线和吸湿曲线组成的，整体形成一个滞回环形状。脱湿阶段土体的基质吸力增加，孔隙水排出，实现水-气平衡。吸湿阶段，水慢慢进入孔隙，基质吸力对应的含水量更大。按照上述土-水特征曲线绘制原理，文中将土体脱湿过程对应的特征曲线表示为图2所示。

非饱和渗流特征模拟完成后，根据模拟结果绘制对应的土-水特征曲线，该曲线中包含饱和含水率、体积含水率、残余含水率共 3 个关键参数，三者之间的关联性如式（11、12）所示：

式（11~12）中，θ表示体积含水率（%），θ′表示饱和含水率（%），θ″表示残余含水率（%），E表示土体基质吸力（Pa），τ₁、τ₂、τ₃ 表示对应含水率的相关系数。

1.4 生成土体抗剪强度衰减预测结果

考虑到影响土-水特征曲线的基质吸力，会对非饱和抗剪强度预测产生很大贡献，而含水率又会影响土体有效黏聚力、有效内摩擦角两项参数（耿佳弟等，2021）。因此，可以从土-水特征曲线入手，建立抗剪强度衰减预测公式：

式（13）中，φ 表示土体抗剪强度（Pa），ρ 表示有效黏聚力（Pa），R 表示净法向应力（Pa），γ表示有效内摩擦角（°），g 表示土体归一化体积含水率（%），f 表示土性参数。

上述计算过程中，土性参数的取值是由土体类型决定的，土性参数加强了抗剪强度与土-水特征曲线之间的联系。为了得到更加真实的土体抗剪强度衰减预测结果，提出先确定一个较大的基质吸力范围，提升土体基质吸力的表达力。

式（14）中，e 表示自然对数函数的底数，ς 表示曲线拐点处斜率的土性参数，f′表示与残余含水率相关的土性参数。

基于式（14），得出符合土体抗剪强度衰减预测要求的预测公式：

通过式（15）所示的预测公式进行计算，即可获取准确的土体抗剪强度衰减预测结果。

2 实验分析

2.1 实验准备

在基于非饱和渗流特征模拟抗剪强度衰减预测方法设计完成后，为了测试这种新提出的预测方法是否可以发挥较大的应用价值，选定湖北省咸宁市通城县某一土体区域为研究区，该区域整体海拔 140 m 左右。通过实地考察可以发现，该研究区域的植被盖度仅为 30%，含水率为 12. 01%，孔隙比为 0.25～0.45，土体内部结构松散，且当前已经出现变形问题，急需进行抗剪强度衰减预测，并根据预测结果提出对应的工程处理措施。

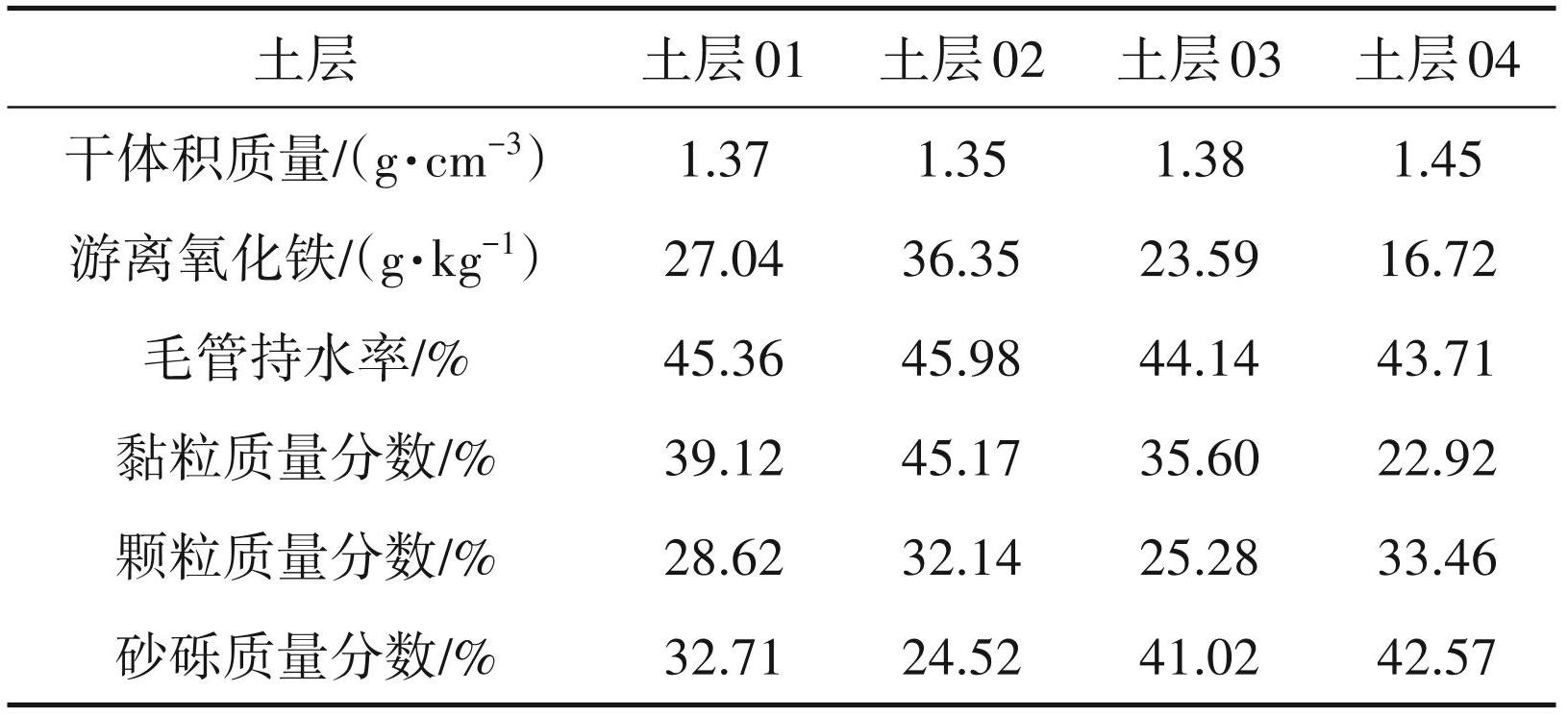
在实验开始之前，针对研究区域的土体进行取样，土体取样现场如图3 所示。根据取样的土体进行分析，确定当前土体主要包括4个土层，各层土体基本性质参数测试结果如表1所示。从表1所示的土体基本性质参数入手，构建非饱和渗流数学模型，并展开非饱和渗流特征有限元模拟。按照上文提出的操作模式，利用 Matlab 软件建立研究区土体有限元计算模型（图4），获取土体的非饱和渗流特征，作为后续抗剪强度衰减预测的依据。

2.2 实验预测结果

（1）抗剪强度衰减预测结果

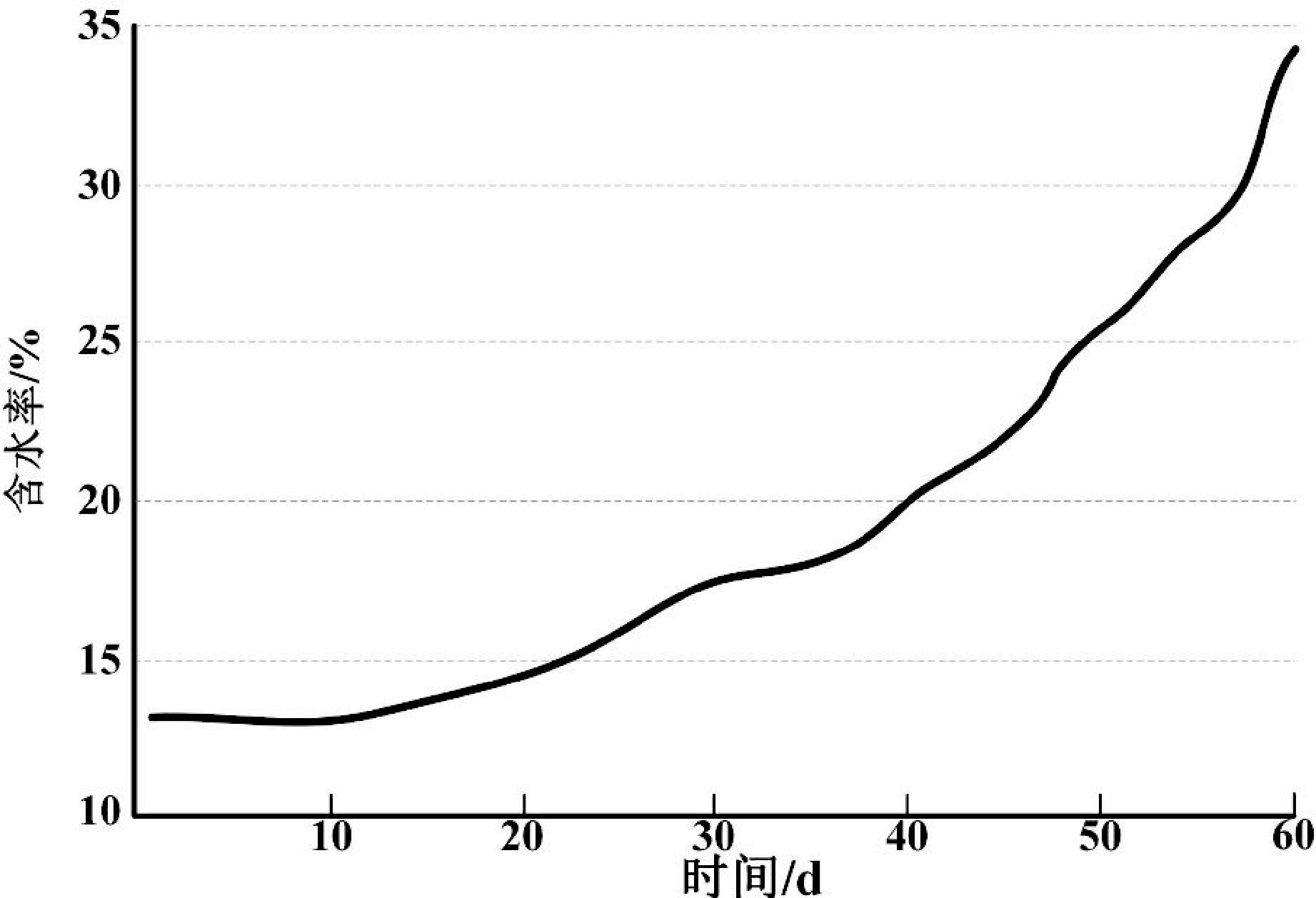
考虑到未来几个月研究区域可能会出现频繁降雨，依托于该模型模拟未来两个月的土体非饱和渗流特征，其模拟土体含水量预测曲线如图5所示。根据图5 显示，土体含水量预测曲线呈现出不断上升的趋势，土体含水率从最初的 12. 01% 增长至 33.98%。

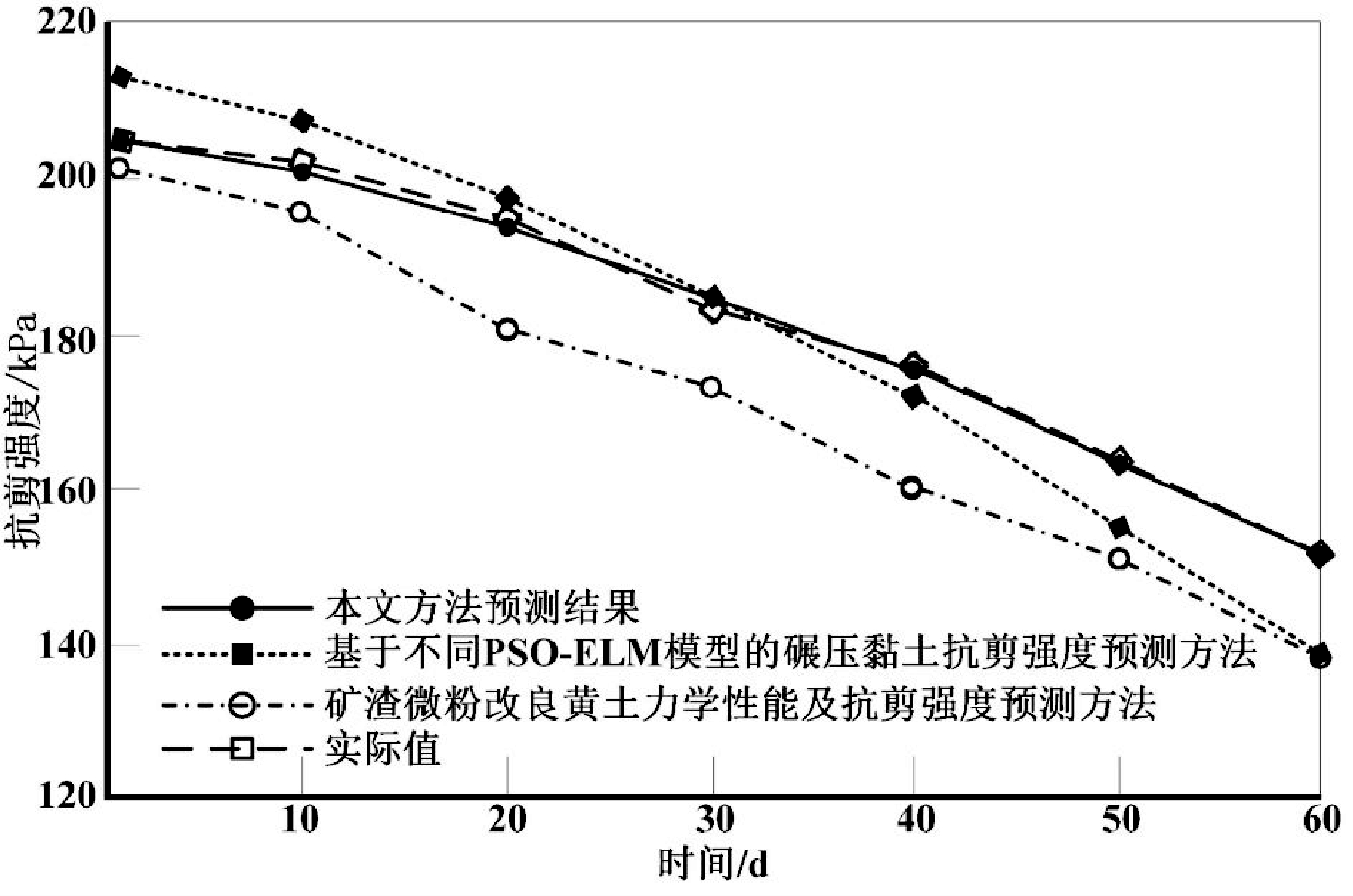
以土体含水量预测曲线为依据，采用本文所提方法进行抗剪强度衰减预测，分别采用基于不同 PSO-ELM模型的碾压黏土抗剪强度预测方法、矿渣微粉改良黄土力学性能及抗剪强度预测方法作为对比方法，不同方法抗剪强度预测结果如图6所示。根据图6可知，基于不同PSO-ELM模型的碾压黏土抗剪强度预测方法、矿渣微粉改良黄土力学性能及抗剪强度预测方法的抗剪强度预测结果，相比实际值存在很大差别，但本文所提方法的抗剪强度预测结果与实际抗剪强度衰减情况几乎一致。

（2）不同方法预测结果对比

为了验证本文所提方法的准确性，对该方法、基于不同 PSO-ELM 模型的碾压黏土抗剪强度预测方法和矿渣微粉改良黄土力学性能及抗剪强度预测方法分别进行测试，将均方根误差（RMSE）作为测试的评价指标，衡量不同预测方法应用性能，均方根误差的表达式为：

式（16）中，M 表示均方根误差，ι表示总预测次数，Y_u表示第u次预测结果，Y_u′表示第u次预测对应的实际值。

结合式（16）对图6 所示的预测结果进一步计算，最终得出本文设计方法预测结果的均方根误差为1.26%，基于不同PSO-ELM模型的碾压黏土抗剪强度预测方法、矿渣微粉改良黄土力学性能及抗剪强度预测方法的均方根误差分别为 11.35%、 19. 02%。

2.3 讨论

（1）非饱和渗流控制方程描述了水在土体中的运动，如果模型中的渗流条件（如水头、渗透率、边界条件等）导致水不断进入土体，那么土体含水量自然会上升。从土体含水量预测曲线可以看出，未来一段时间内可能会受到降雨等因素的影响。通过模拟土体含水量变化，可以更好地评估在不同气候和地下水条件下的工程风险，为工程设计和施工提供科学依据。

（2）通过水体质量守恒方程和非饱和渗流控制方程建立的数学模型，能够准确描述土体中水分的迁移和分布，定义的第三类边界条件考虑了实际工程中土体与外界环境的相互作用，如降雨、蒸发等，这些因素直接影响土体的含水量和抗剪强度。因此，在气候变化和极端天气事件频发的背景下，该方法抗剪强度预测结果也较为准确，有助于评估和预测土体在不同环境条件下的稳定性，为环境保护和灾害预防提供科学依据。

（3）采用空间域离散和时间域差分原理，结合 Chebyshev网格法，能够有效地处理复杂的几何形状和边界条件，提高计算精度。在实际工程中，如边坡稳定、基础设计、地下水管理等领域，通过预测土体抗剪强度的衰减，可以更准确地评估工程的安全性和稳定性，从而采取相应的防护措施。

3 结束语

由于越来越多的工程施工区域位于非饱和土体环境中，对工程的稳定性产生极大威胁。为了进一步提升工程安全性，提出一种基于非饱和渗流特征模拟的土体抗剪强度衰减预测方法。

（1）针对所构建的非饱和渗流控制方程，规范了非饱和渗流过程中的流量范围，以此设定第三类边界条件，实现非饱和渗流数学模型的构建。

（2）通过获取的土体特征变化情况的有限元计算模式，采用了 Chebyshev网格法，优化了模拟模型的均匀网格，获得模拟方案，并绘制了土体土-水特征曲线，以此建立抗剪强度衰减预测公式，实现了土体抗剪强度衰减预测。

（3）实验结果表明，本文所提方法抗剪强度预测结果与实际抗剪强度衰减情况几乎一致，且预测结果的均方根误差小，证明了该方法的优越性。

参考文献