0 引言

滑坡被认为是当今世界上最危险的灾害之一 （杨天鸿等，2020）。山体滑坡几乎发生在人类居住或工程活动发生的所有地区。每年，山体滑坡都会在世界各地造成巨大的生命和财产损失。导致山体滑坡的因素有很多，例如地震活动引起的土壤破坏、地下水位上升和河流持续侵蚀（郑宏等，2002）。除了自然斜坡和山体滑坡外，人类的工程活动也可能导致山体滑坡。随着露天坑深度的增加，斜坡高度逐渐增加，导致露天坑斜坡急剧上升（郑颖人等， 2006）。高坡和斜坡的稳定性不仅受到岩石和土壤特征、地质特征结构和条件等内部因素的影响，还受到降水、地下水、爆炸性振动、斜坡相关参数等外部因素的影响（陈毓和周西华，2019）。存在坍塌、倾倒和山体滑坡的固有风险，这对矿山生产安全构成重大风险（李建华，2021）。因此，计算和分析露天矿山斜坡的稳定性对于新建或扩建矿山的生产安全和安全设施设计变得越来越重要。本文结合开采条件和开采场地的边坡角度等（欧湘萍等， 2009；颜红迪等，2023），对西藏某铜矿高陡边坡的稳定性进行了定量计算和分析，对目前的边坡稳定性进行了研究，为该矿后续的安全生产提供参考。

1 矿区概况

矿区地处雅鲁藏布江一级支流拉萨河流域南部，位于拉萨河南侧甲玛河支流——甲玛西沟上游的支沟荣木错拉河上游及两侧山地，属极高山区，地貌类型中等复杂，分布有构造剥蚀极高山地貌、河谷侵蚀堆积地貌及冰川地貌。

矿区极高山构造剥蚀地貌区，地形切割较强烈，山脊尖棱，山体斜坡多为直线坡，斜坡表面倒石堆、岩屑流（碎石流）、坡积堆、坡积裙等十分发育； 植被以高山草甸为主，并有少量高山耐寒苔藓，覆盖率 20%～30%。该地貌区地势总体为东、西高山脊，中间低的冰川槽谷，南西侧为山体最高点—该矿区驻地以东、测试控制点 GPS11号山脊点以南山顶，海拔 5565 m，两侧山脊、斜坡陡峻，坡度 30°～35°；荣木错拉河上游为冰川槽谷，槽谷一般宽 150～500 m，纵坡降 5°～15°。最低点为荣木错拉河在矿区外围北东段汇集流入甲玛西沟处标高 4930 m 处，相对高差约 735 m。区内主矿体主要分布在荣木错拉河流上游河谷及两侧山坡。

矿区东南侧、西侧分别为浪母家果沟、且津朗铁格沟河谷侵蚀堆积地貌，河谷宽 150～200 m，河床向北倾斜，坡度 5°～10°，两侧山前地带残存侧碛垅，中部为平缓的冲洪积阶地侵蚀堆积地貌，阶面宽 100 m 左右，略有起伏，向河流下流方向倾斜，坡度10°～15°。阶地前缘陡坎高1～3 m。

该矿区平均海拔大于 5200 m，属极高山区；区内冰缘地貌特征明显，发育不同时期的冰斗、角峰、悬谷、冲沟、侧碛垅、终碛垅以及倒石堆、寒冻石流 （碎石流）、坡积堆、坡积裙等。地形坡度一般 30°～40°，局部形成陡岩。

矿区地形复杂，露天矿坑中的岩层相对简单。然而，露天矿坑的地质条件是中等至复杂的，属于被风化和裂缝潜水顶板直接充水矿床。预计露天矿坑中的水流超过300 m³ /h，水文地质条件应适中。铜矿和周围岩石坚硬，结构简单，各种类型的高级机身岩石。该地区气态岩石很强，该地区气态厚度很大，影响了页岩的稳定性，但大多数气态强的半开放采矿区在对稳定性影响不大的地层中幸存下来。地质工程采矿的主要问题是采矿过程中存在断裂带密度。由于松散稳定性差和岩石断裂，需要各种支撑方法。

转化后的液化气在采矿中占主导地位，周围的岩石正在发生变化和演变。改变主要由浮力组成的周围岩石后，岩石的强度和硬度增加，岩石稳定性增加。天然矿区的斜率，斜率切割，人工斜率基本稳定。目前，碎片流、山体滑坡、山体滑坡等负面物理和地质现象尚未形成。然而，在降雨量充沛和季节性土壤融化的地区（急坡或急坡至慢坡），可能会发生小规模的侵蚀性坍塌或碎片流动，这不利于斜坡的稳定性。存在许多工程和地质问题，例如断裂区域密度分布不稳定。

设计确定的露采边坡参数如下：（1）台阶高度 15 m；（2）终了并段台阶高度 30 m；（3）终了台阶坡面角 65°～70°；（4）清扫运输平台宽度 8～18 m；（5） 运输道路宽度26~38 m，坡度8%，转弯半径≥30 m。

2 边坡分区及稳定性分析方法选取

2.1 边坡分区

边坡分区是根据边坡形状、位置、高度、岩体优势结构面产状以及与边坡的组合关系、工程地质岩组的分布特征、不连续面特征、地下水状况等要素进行的。划分原则是在同一地质工程区内划分类似元素或相同区域（虎万杰，2020）。

本文将该矿区露天开采境界分为3个边坡稳定性分区（图1），其中：I 区（北部）边坡采高达 135 m，沿最高边坡位置选取 2 条剖面，边坡高度分别为 105 m 和 136 m；II 区（西部）边坡的采高推进较快，边坡高度已达 150 m，沿最高边坡位置选取 1 条剖面，III区（南部）边坡较缓，边坡高度约 65 m，选取 1 条分析剖面。图1 中蓝线为分区界限，红线为分析剖面（姜德义等，2005）。

2.2 边坡稳定性分析方法

边坡稳定性计算是最终为边坡稳定性研究提供定量指标的分析过程，是边坡研究的核心（马毓婷等，2022）。它是在工程水文地质调查与分析、岩石力学试验研究与工程处理、破坏模式分析等各项工作的基础上，获得符合客观实际的几何参数和各种力学参数，最终计算出表征边坡稳定程度的定量指标（赵亭和王畅，2019）。

边坡稳定性分析的极限平衡法是土壤力学中的经典问题之一。极限平衡法采用分片的基本思想，假设边坡处于极限平衡状态，寻找最危险的潜在滑动面，并计算相应的最小稳定系数。这方面的理论研究逐渐变得更加严格，从早期的瑞典方法到适用于圆形滑动面的毕晓普方法，再到适用于任意形状并完全满足静态平衡条件的 Morgenstern-Price 方法。边坡稳定性分析方法主要包括：简化毕晓普法、Spencer法、Janbu法、Morgenstern-Price法、Sarma 法、Army Corps法、Lowe-Karafiath法、瑞典圆弧滑动法、不平衡推力法等（黄帅等，2015）

各种分割方法的最大差异在于对相邻块体之间的内力相互作用的假设不一致，即使用不同的方法将超静态问题转化为静态问题（宋波等，2014）。这些假设的物理含义不同，它们所能满足的平衡条件也不同，从而产生了不同的适合计算的场景。对各种方法进行不同程度的比较分析，一般认为：

（1）瑞典法在平缓边坡或高孔隙水压力情况下得到的边坡稳定性系数误差较大。

（2）简化 Bishop 法在大部分情况下均可获得与通用条分法基本相同的结果。其局限性主要是仅适用于圆弧滑裂面及有时会遇到数值分析问题。当简化 Bishop法的结果比瑞典法小时，可以认为此时存在数值分析问题。

（3）Spencer法在个别情况下会出现收敛困难的问题，如土压力问题、滑裂面包含拉裂缝并充水等情况。

（4）仅满足静力平衡条件的方法的结果对所假定的条间力方向极为敏感，不同的条块间方向获得的稳定性系数差别较大。

（5）满足全部平衡条件的方法（如 Morgenstern-Price 法、Sarma 法）在任何情况下都是精确的（除非遇到数值问题外）。因此，计算中尽量使用同时满足力和力矩平衡的条分法。

（6）各种稳定性分析的图表，在边坡几何条件、容重、强度指标和孔隙水压力可以简化的情况下可得出有用的结果，其局限性在于使用图表时需要对上述条件进行简化处理。使用图表的优点在于可以快速得到稳定性系数。通常可先使用这些图表进行初步核算，再使用计算机程序进行详细核算 （刘金龙，2017）。

大量研究和工程实践证实，运用同时满足力和力矩平衡的严格法计算结果较相近，各种非严格法，除简化 Bishop 法和不平衡推力法外，各种方法都有较大误差。运用同时满足力和力矩平衡的计算方法得到的稳定性系数和 Bishop 法的结果非常接近；瑞典法和 Janbu 法在的结果受条块数目的影响较小，但其结果较同时满足力和力矩平衡的方法偏小。

因此，在边坡稳定性分析中，使用 Morgenstern-Price 法和 Bishop 法等极限平衡条分法得到的稳定性系数较合理和可靠。

（1）简化Bishop法

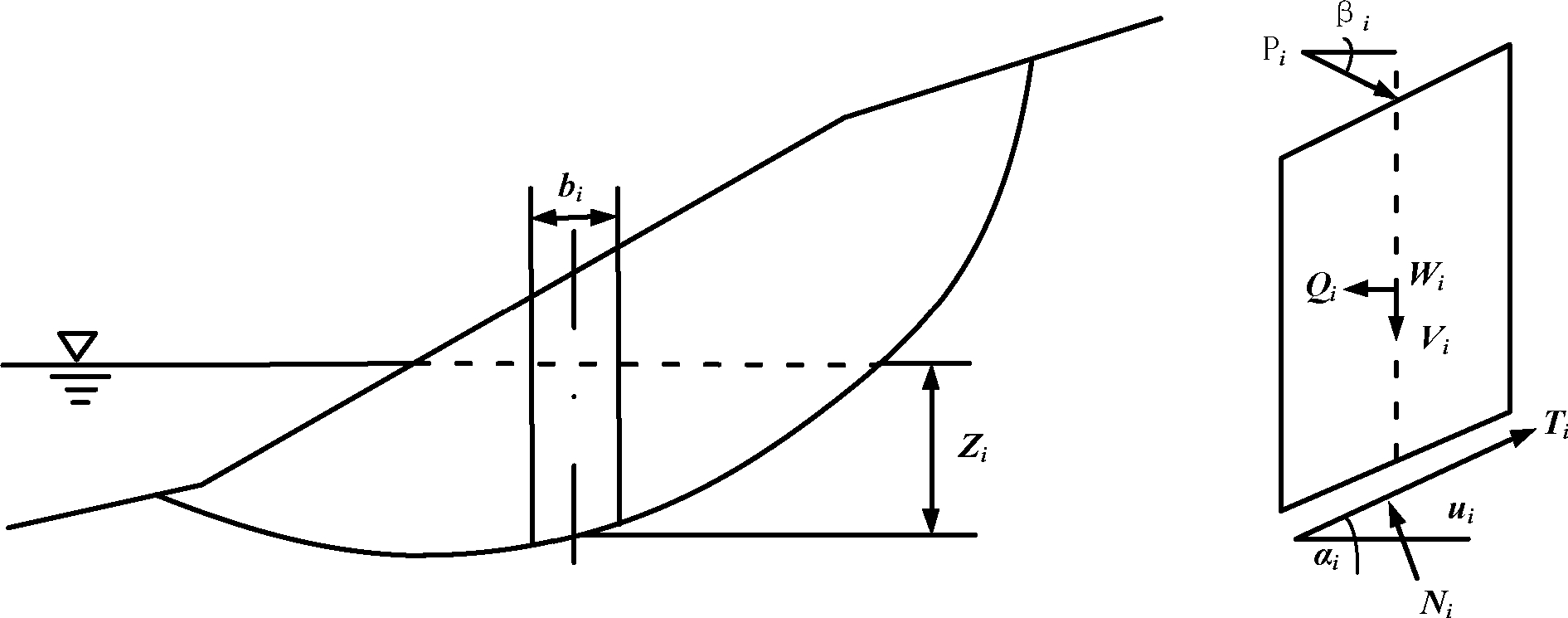
简化Bishop法计算简图见图2所示。

式（1）中：c_i、φ_i —分别为第 i 条块岩体的黏结力和内摩擦角；W_i —条块i的重量；L_i ——条块i的底边长；Q_i —作用在条块 i上的水平力，可为地震爆破作用等效水平力或垂直裂隙上的静水压力；α_i —条块i 底边与坐标轴水平面的夹角；U_i —条块i上作用的水平力（王凯，2012）。

（2）Morgenstern-Price法

摩根斯坦—普赖斯法是假定两个相邻的土条之间存在法向力和切向力，假定这两个力之间在水平的方向存在一定的函数关系，该函数关系可以表达为（式2）：

式（2）中：X—土条之间的切向力；E—土条之间法向力；λ—待定常数。

在摩根斯坦-普赖斯法中取 f（x）=0 时，其计算结果与简化 Bishop 法相同。该方法理论上比较严密，适用于任意形状的滑裂面，全面满足力的平衡条件和力矩的平衡条件，适用于滑面为折线形的边坡的稳定性计算。

3 边坡破坏模式及滑面类型

破坏模式的确定是边坡稳定性研究的一个重要方面。不同的破坏模式适用于不同的稳定性分析和计算方法，不同的稳定性判别会导致对边坡稳定性的不同结论。

在分析一般露天边坡的稳定性时，边坡破坏模式的确定主要考虑岩石类型、岩体结构面类型、主导结构面产状和边坡结构参数等因素及其关系（武飞和胡崴，2023）。一般而言，岩石边坡的主要依据是岩体结构与边坡的组合关系，主要遵循以下原则：

（1）根据现有的工程地质和水文地质数据，尝试识别“确定面”或“特征面”，即与边坡内的不连续或软弱夹层、断裂带和岩石控制面相互连接的潜在剪切面，其形状、位置和大小已与边坡的自由面确定。这些潜在的剪切面主要受工程地质和力学特性的控制。

矿区内有两条主断层F4和F5，主要位于B区北部。F4 位于北部 B 区顶部约 200 m 处，F5 位于 B 区斜坡顶部。断层与边坡的倾斜度相反，对裸露的矿坑影响有限。

（2）根据节理裂隙组的数量、产状或岩石强度，如果满足以下条件之一，则边坡破坏模式可确定为圆弧破坏模式：

破坏模式的确定是边坡稳定性研究的一项重要内容，不同的破坏模式适用于不同的稳定性分析计算

①均匀松散介质、冲积层、大型岩层破碎带；

②有至少三组产状各异的软弱结构面，同时与边坡面不为同向；

③强风化碎裂结构的岩体；

④某些强度很低的岩石边坡；

⑤软弱面的产状各异且均不与边坡面同向；

⑥两侧面脱开。

岩质边坡潜滑面的形状一般来说不会是很严格的圆弧形，经验已表明：大量滑坡实测的滑动面都可近似地表示为垂直裂隙加圆弧形（高庆等， 2023；张志文，2023）。

（3）楔形滑动破坏判别

楔形四面体通常由两组弱面组成，楔体沿某弱面滑动的判别准则如下：

①两结构面中必定有一个倾角较大的陡立面，通常为直立的最小断裂面；

②最小断裂面被拉开后，楔体沿另一结构面滑动；

③沿该结构面滑动的面上的内摩擦角要小于该面的倾角。

综上所述，该铜矿矿区露天边坡的破坏模式为垂直裂隙加圆弧形破坏，边坡稳定性研究时应按圆弧形破坏模式进行分析。

4 边坡稳定性极限平衡分析

4.1 分析剖面与计算工况

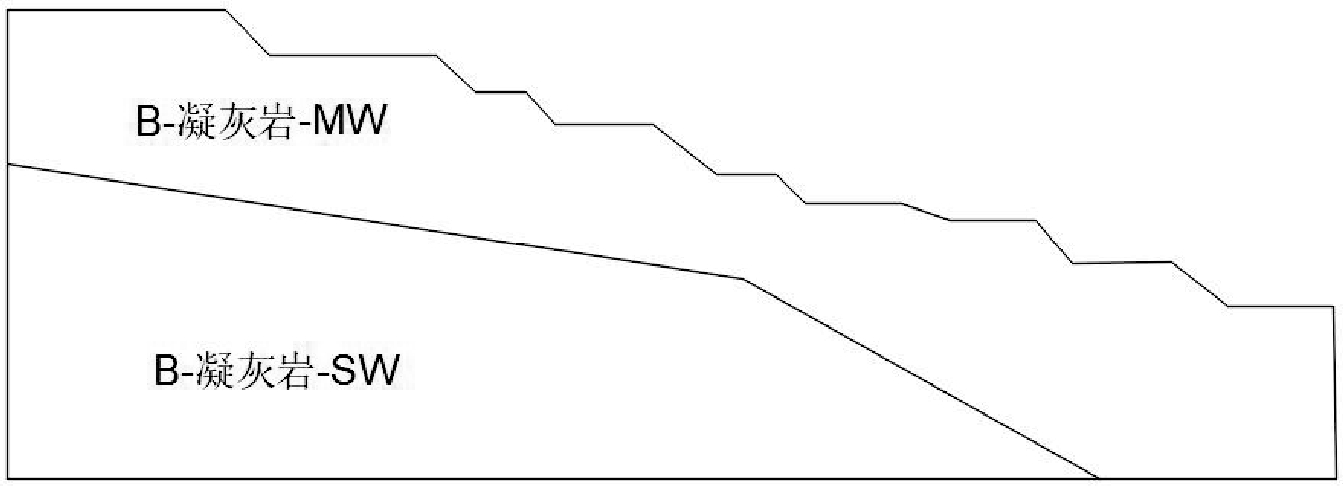
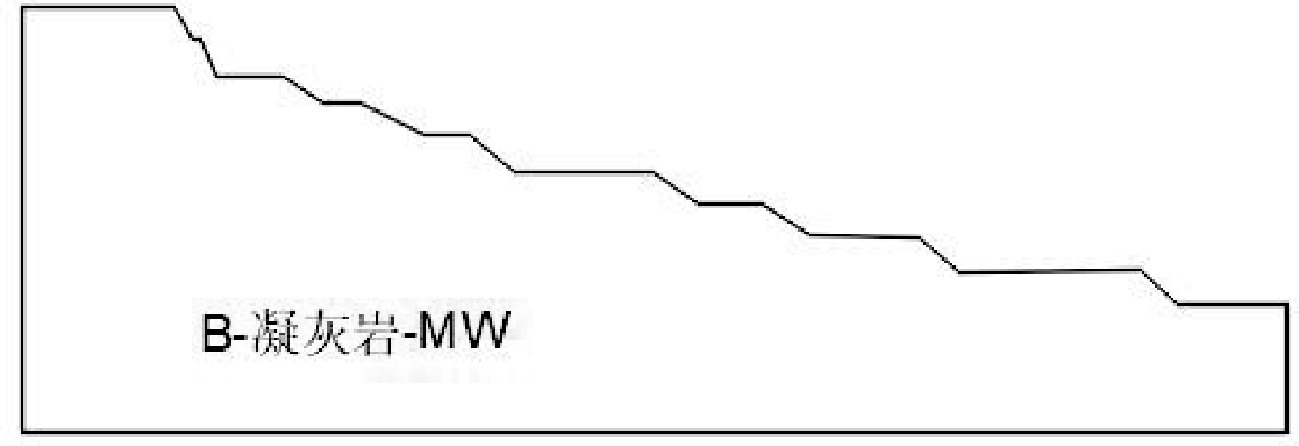
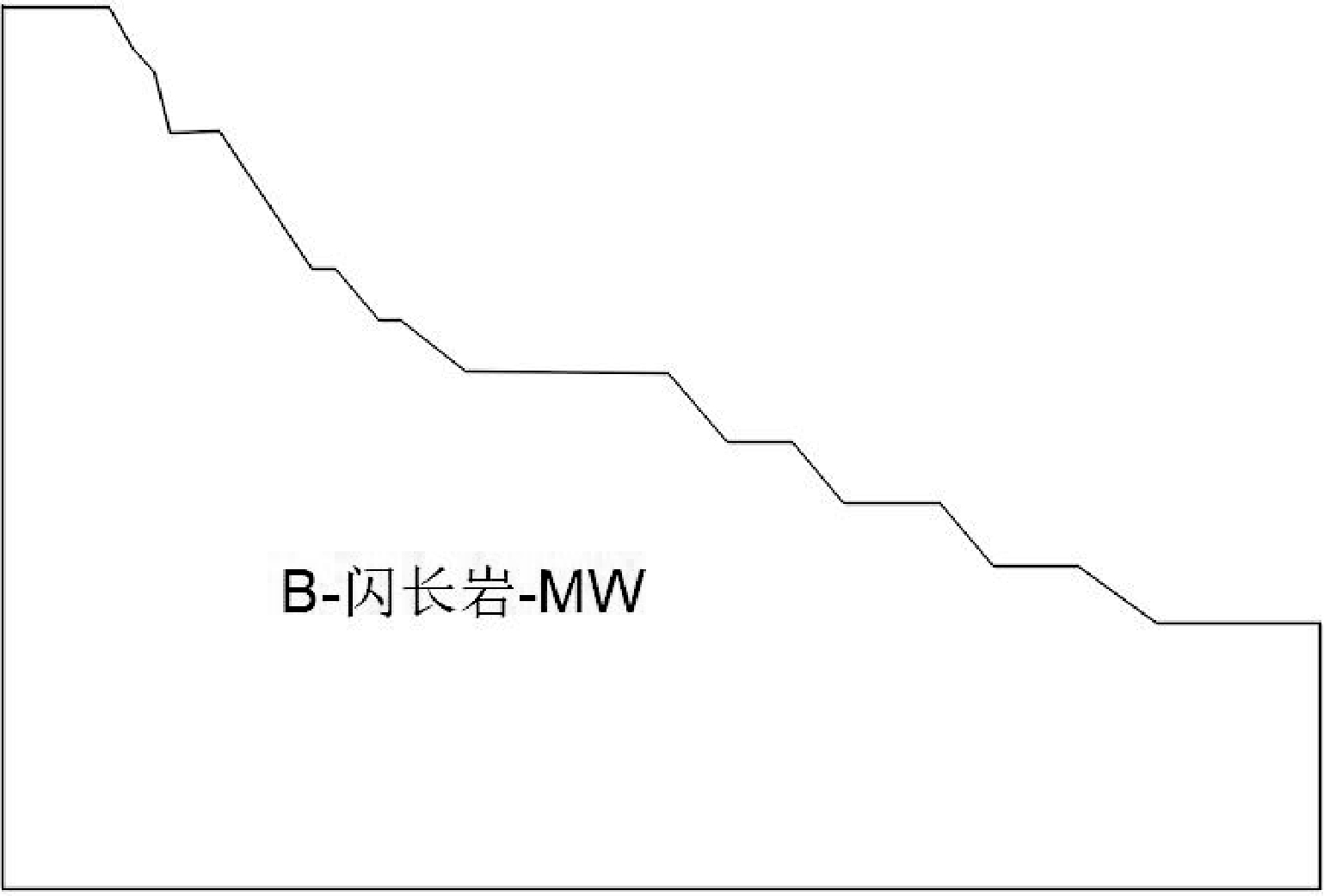
根据前述的露天边坡稳定性研究分区，本次对该矿区边坡进行极限平衡分析的剖面数为 4 个（图3~图6），即 I 分区的 1-1、2-2 剖面，II 分区的 3-3 剖面，III分区的4-4剖面。

对该矿区现状边坡的 4个剖面进行如下 3种受力情况的分析：荷载组合 I：自重+地下水；荷载组合 II：自重+地下水+爆破振动力；荷载组合III：自重+地下水+地震力。

4.2 岩体物理力学参数及许用安全系数

通过对该铜矿岩石力学参数相关的一些试验结果的工程处理，综合选取的岩体力学参数（表1）。其中：A、C 区凝灰岩组物理力学参数选取较 B 区稍高，因 A、C 区凝灰岩强度较高；结构面参数取为 c= 0.1 MPa，φ=25°。对矿区内的强风化层及第四系物理力学参数选取为参考大型直剪试验结果而定。

该铜矿设计最终边坡最大高度均在585～945 m，根据《非煤露天矿边坡工程技术规范》（GB 51016-2014）划分标准，该露天边坡属超高边坡，边坡危害等级为Ⅰ级，边坡安全等级划分为Ⅰ级。

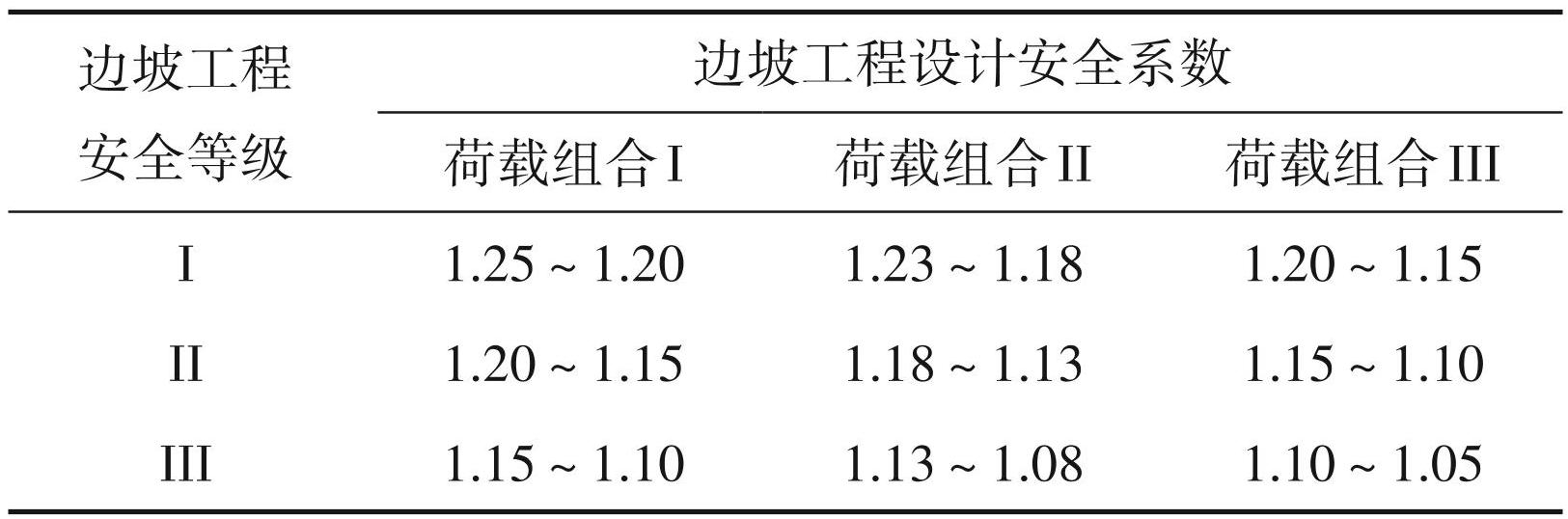
对台阶边坡和临时性工作帮，允许有一定程度的破坏，设计安全系数可适当降低，根据《有色金属采矿设计规范》（GB50771-2012）的规定，露天边坡安全系数K的选取，可按表2选取。

综合分析，该铜矿边坡的勘探程度为一般，确定的许用安全系数[K]如下：

注：1. 荷载组合Ⅰ为自重+地下水；荷载组合Ⅱ为自重+地下水+ 爆破振动力；荷载组合Ⅲ为自重+地下水+地震力（习泳等。2021）。

①正常情况下：[K]=1.20；

②VII度地震时：[K]=1.18；

③Ⅷ度地震时：[K]=1.15。

若剖面计算所得的安全系数：K＞[K]时属稳定；1＜K＜[K]时基本稳定，K＜1 时不稳定（马可， 2021；王家全等，2021；贾文松等，2022）。

4.3 边坡剖面的极限平衡分析

根据前文分析，本文选用 Morgenstern-Price 法和简化Bishop方法进行边坡稳定性分析。

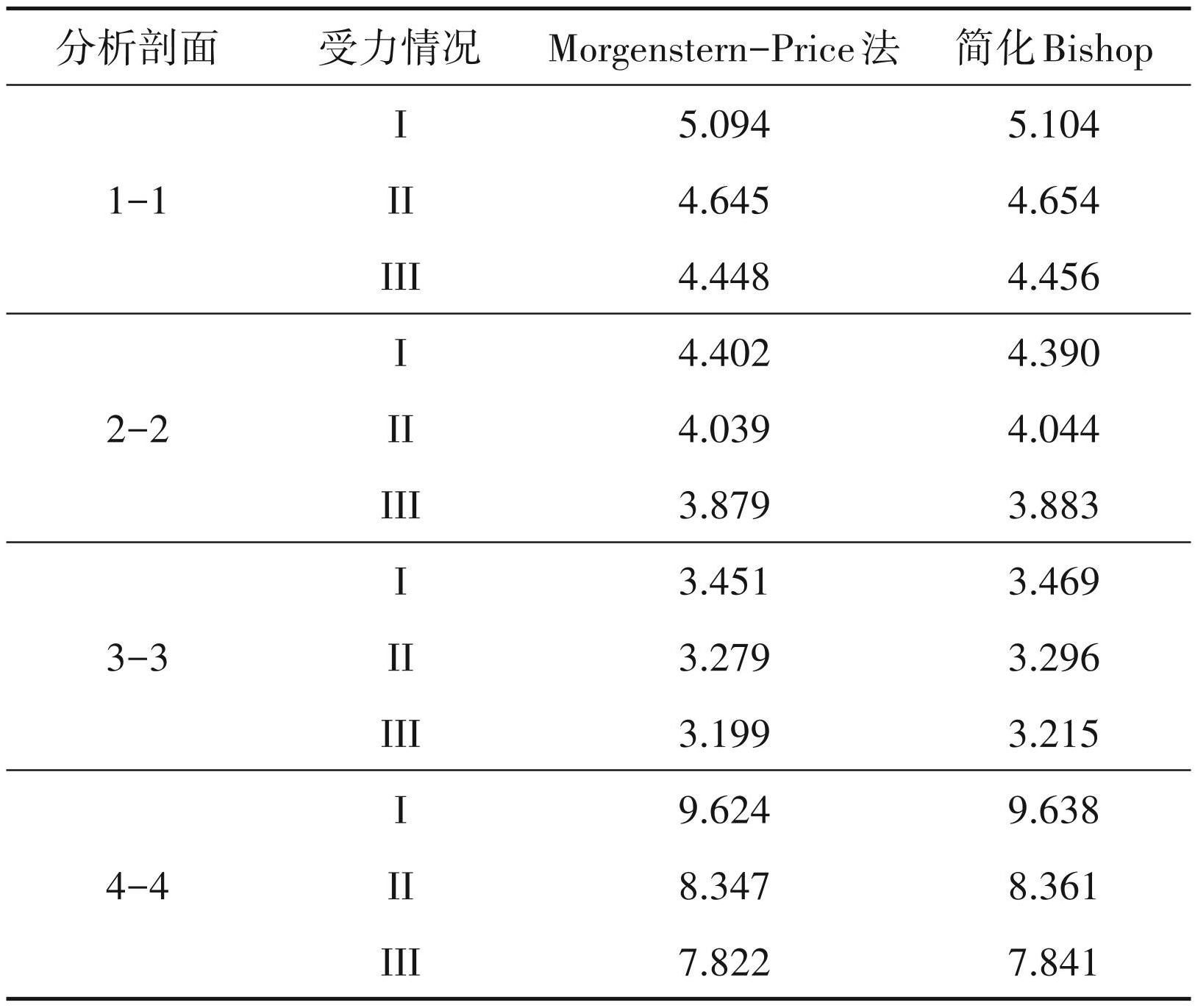
该矿现状边坡 4 个剖面在 3 种不同受力条件下，边坡稳定性的极限平衡分析结果如表3所示。

根据表3 结果，所有分区边坡剖面在荷载组合 I、II、III情况下，计算得到的安全系数均大于相应许用的安全系数。

5 结论

（1）通过以往的地勘资料以及现有的地质资料总结分析，区内岩体风化较强烈，风化带厚度较大，影响岩体稳定，但强风化带拟大部被露采剥离，风化层对稳定性影响小。

（2）按照分区原则，将现状边坡划分为 3 个区域，并剖分了4个边坡稳定性分析剖面。

（3）以安全系数为指标，通过分析4个代表性剖面，分别采用了 Morgenstern-Price 法和简化 Bishop 对初步设计下的边坡进行极限平衡计算，分析了三种荷载组合下的边坡极限平衡稳定性，计算得到的安全系数均大于相应许用的安全系数，说明目前现状边坡稳定性满足规范要求。

参考文献