0 引言

西部高寒高海拔地区的矿产资源开发是中国西部大开发的重要组成部分（王光东，2016；杨越， 2019）。这些大型露天矿山边坡可能出现的滑坡 （梁小涛，2018）、泥石流等工程灾害已引起人们的广泛关注。因此，露天矿山开采边坡的稳定性已成为岩土工程的重要技术问题之一，而边坡设计剖面 （牟义等，2023）是否合理，也是研究的重要内容。

由于露天矿山边坡岩土介质（张银铂和宫凤梧，2024）本身的复杂性，也是由于露天矿山边坡工程（夏元友和李梅，2002）客观环境的复杂性，一般而言，在任何露天矿山边坡设计中（冯锦艳等， 2005），都没有一个绝对精确合理且完全切合工程实际的总体坡面角度值（王家臣等，2005）。而一般情况下，要寻找合理的边坡角，是通过计算边坡的安全系数来实现的（陈祖煜等，2001）。在确定边坡的安全系数过程中，迄今为止，在许多实际工程设计或研究中，往往采用工程类比法，或使用各种数值分析方法通过计算机进行计算，或经过对比分析后给出一个近似合理的边坡安全系数值。而在此过程中，不乏有些边坡安全系数值经实践检验表明与工程实际情况相差甚远。

本文以中国青藏高原某高陡矿区设计边坡为例，采用两种极限平衡法及强度折减法，以安全系数为指标，通过极限平衡计算的结果验证强度折减法计算结果的可靠性，在此基础上，重点分析强度折减前的有限差分计算结果，分析在开采、爆破及地震荷载作用下设计边坡的变形规律，从多方面来论证设计参数的合理性，研究结果可为后续设计参数优化提供参考。

1 工程背景

矿区位于青藏高原冈底斯山脉东段，中部为沿巴尊岩体西—加冬—红头山—铜铅山—则古朗北东走向的地表分水岭，东西两侧被斯布普沟及甲玛沟深切，区内主要沟谷沿此分水岭近乎垂直两沟，呈梳状排列于分水岭两侧。地形坡度一般在 30°～40°，最陡达50°左右，局部沟谷受断裂构造影响形成高大陡崖。研究区域地形起伏较大，地势总体中间高两侧低，最高点海拔标高为 5220 m，最低点地面标高在5015 m左右。

矿区地貌属于藏南高原区，地貌类型以高山构造剥蚀地貌为主，冰缘地貌、构造侵蚀—溶蚀地貌、侵蚀堆积地貌次之，此外，甲玛沟及斯米沟低缓地带分布有小面积的湿地。高山构造剥蚀地貌分布于研究区主要沟谷两侧，区内山高坡陡，地形切割强烈，山峦连绵起伏。区内冰缘地貌特征显著，在各大支沟中均可见发育不同时期的冰斗、角峰、悬谷、寒冻石流、冰围谷、冰蚀洼地等冰川地貌特征。构造侵蚀—溶蚀地貌主要分布于斯米沟、科朗沟、盘羊沟及灰普等沟谷，地形特征与高山峡谷相似，早期岩溶比较发育，溶洞、溶沟、溶槽、溶蚀裂隙等常见于山顶或山坡构造发育处。侵蚀堆积地貌主要分布于甲玛河和斯布普河河床及其两侧支沟沟口开阔地带。

该地区气候属典型的大陆性高原气候，属温带高原半湿润轻霜冻气候区，昼夜温差大，空气稀薄，日照充足，干湿季明显，夏季温和湿润，冬季寒冷干燥，气候多变，全年无绝对的无霜期和无雪期。

2 露天采场边坡稳定性分析方法

2.1 极限平衡法

（1）不平衡推力法

不平衡推力方法也被称为传力系数法或剩余推力法，为国内自主创新的边坡稳定性分析方法，现已被纳入国家及行业的相关标准，作为推荐的应用方法。鉴于其计算过程的便捷性，且能够为防治滑坡提供所需的设计推力，此技术在滑坡的评估与处理领域获得了广泛采纳。

（2）M-P法

1965年提出的摩根斯坦-普莱斯方法（简称M-P 法），是一套严密的分块法，取消了关于滑动面形态或静态平衡的假定。具体而言，该方法从对复杂滑动界面的剖析入手，推导出一个满足力和力矩平衡的微分方程组；随后，它设定一个函数关联着相邻分块之间的剪切力与垂直力比例与水平方向位置的关系；最终根据滑移体周边的限制条件，计算出边坡的安全系数。

根据M-P法，必须确保各个区块在力和转矩方面均达到平衡状态，这一过程通过连续的迭代计算来完成。它不仅符合整体结构的力学均衡原则，而且是一种较为精确的分条技术。尽管该方法同样遵循整体转矩均衡的公式，但并未直接应用于简化计算。由于没有利用整体转矩均衡来减轻计算的复杂性，该方法因此能够适用于各种形状的滑移面，是一种普遍采用的分段策略。

2.2 强度折减法

1975 年，Zienkiewicz 携手同行在土木工程分析的领域首次提出了在抗剪能力上与设定静载荷下形成的实际剪切参数的比值，即抗剪强度折减系数。这一系数描绘的是：在给定外力作用不变的情况下，滑坡土体所能展现的最大抗剪强度与受该外部载荷效应产生的实际剪应力之比。假设滑坡区域内所有土质的剪切强度降至一致的水平，则此系数进一步演变为衡量整体边坡稳定的重要参数。

强度折减方法成功整合了考虑结构额外的强度和坡体稳定系数的过程。此技术在用有限元方式进行模拟分析时，避免了确定具体的滑移面形状与位置。随着大量工程实践的推广，这项技术的广泛适用性日益显现。具体操作时，需要将坡面上原有的强度参数（即黏聚力和内摩擦角）均等降低一个系数F后，得到一组更新后的参数，这些参数被输入到模型中，并经过连续迭代运算，用稳定性评估准则确定匹配的F值。该F值意味着坡体维持稳定所需的最小安全系数，是坡体在达到失稳条件下可能发生剪切破坏的界面，并允许对可能的滑移面进行预测。

3 数值模型的建立及计算结果分析

3.1 边坡稳定性计算剖面的建立

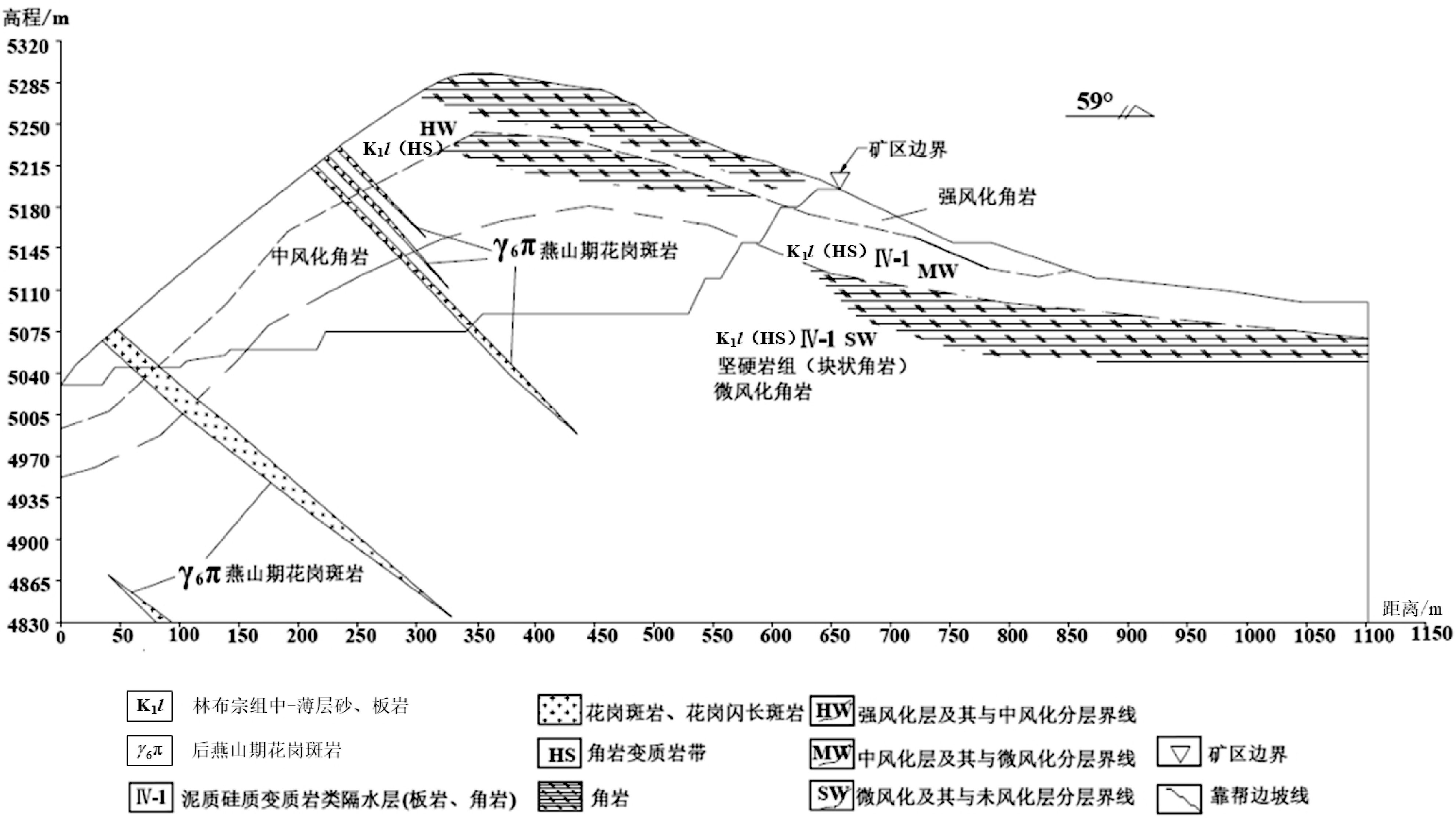
在工程地质分析的基础上，根据矿区工程地质条件的差异性，甲玛铜多金属矿露天采场边坡稳定性计算选取的具有典型代表性的剖面：1-1′（模型延伸至负地形或相对平缓的位置，减小尺寸效应的影响，且剖面线与边坡走向垂直），进行矿区边坡的整体稳定性分析，边坡工程地质剖面图如图1所示。

3.2 数值模型力学参数的确定

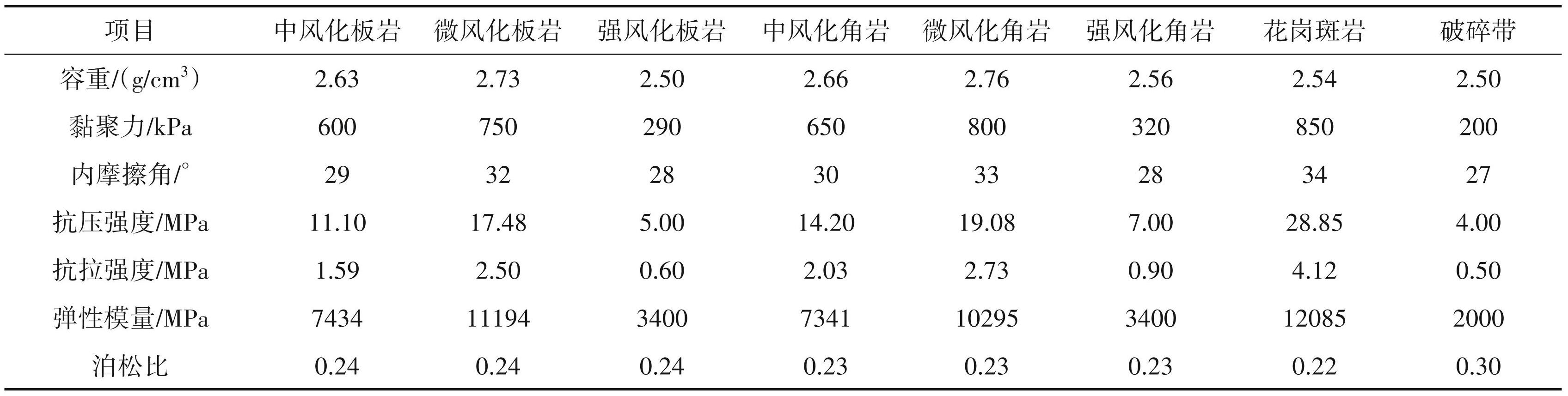
根据岩石力学试验结果，结合矿区实际情况、工程地质条件、室内物理力学试验，利用H-B准则等，综合确定矿区边坡的岩土体物理力学参数（表1）。

3.3 极限平衡法计算结果分析

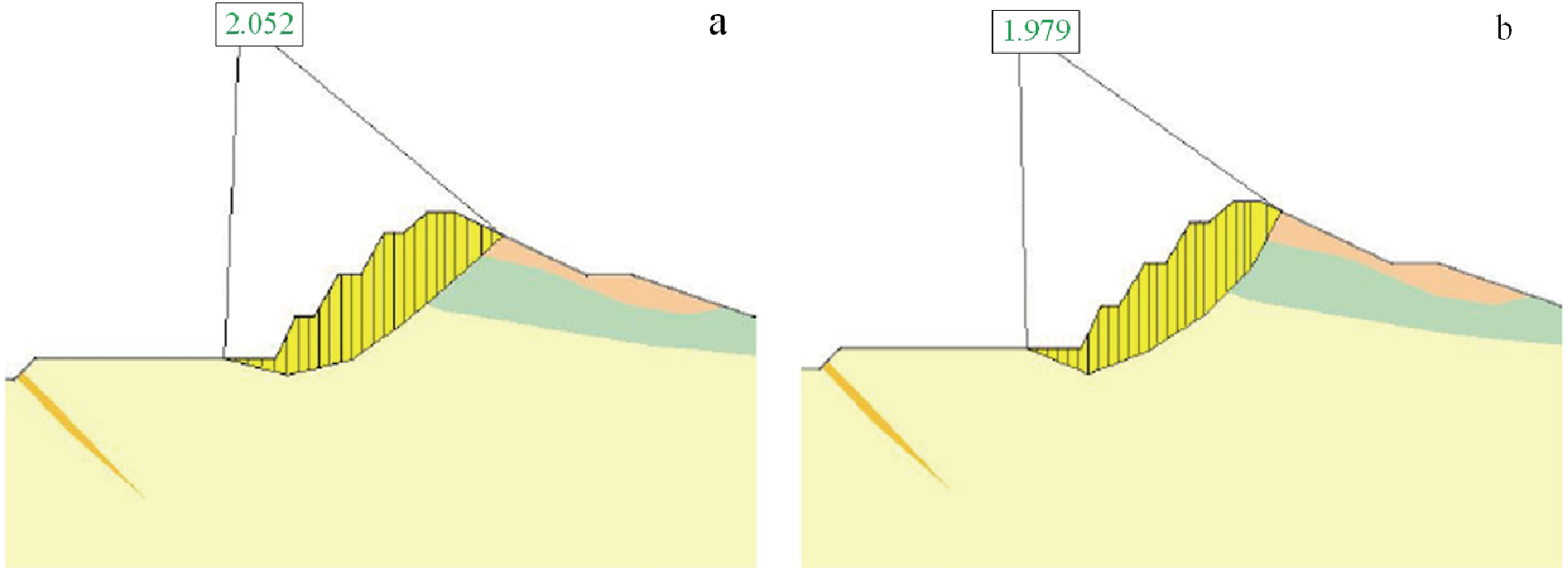
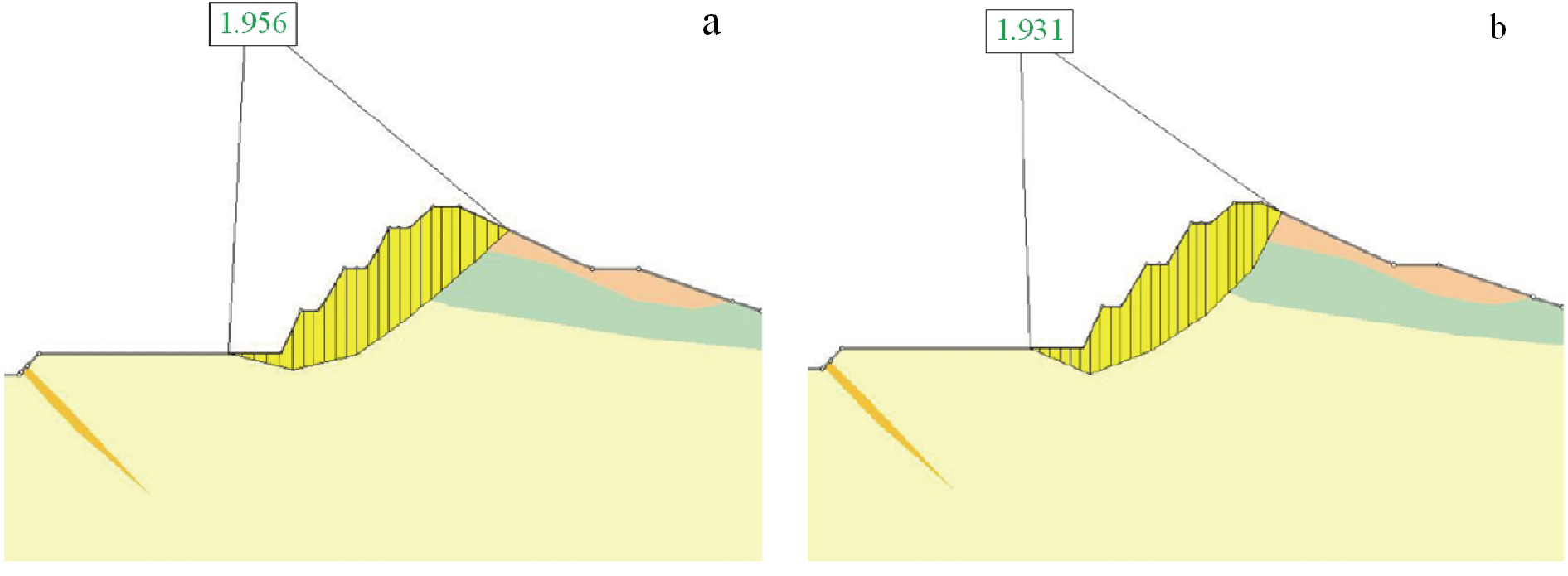
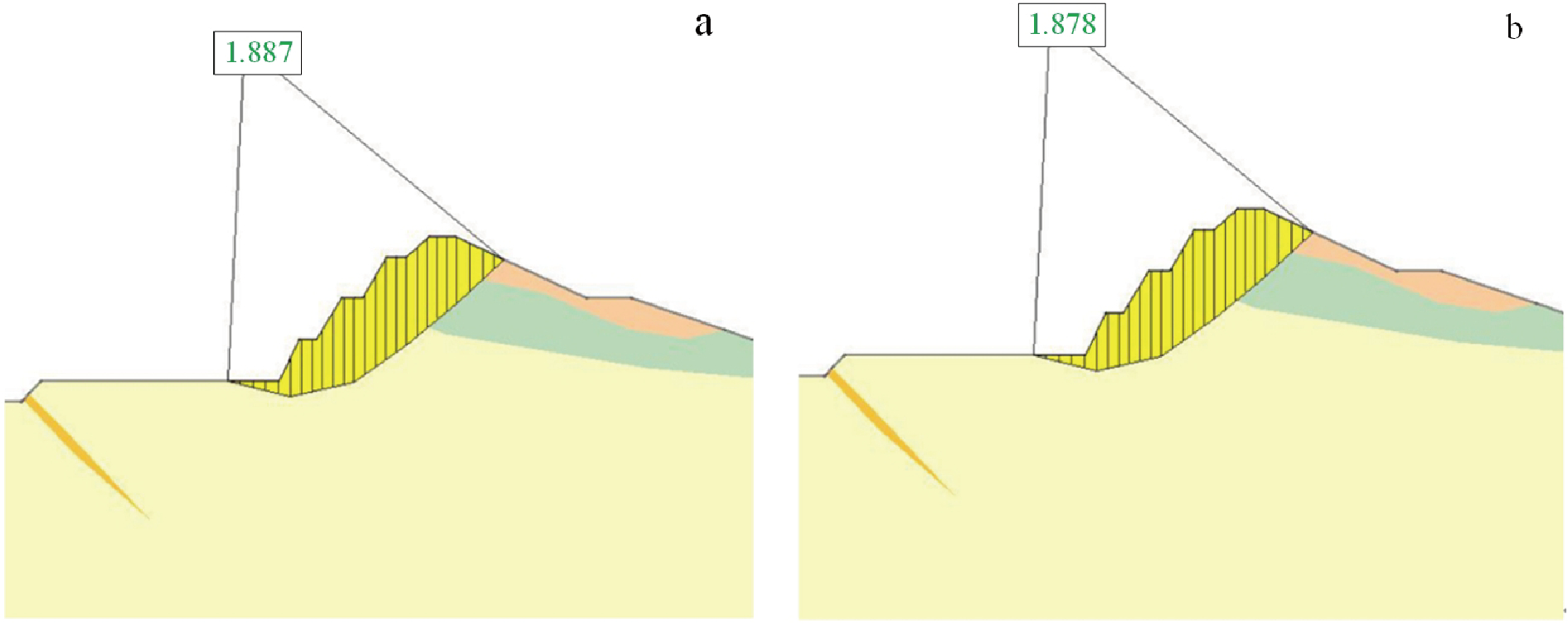
根据Slide稳定性分析计算结果，结合矿区各剖面现状实际情况，各个剖面的稳定性系数在荷载组合Ⅰ（自重＋地下水）、荷载组合Ⅱ（自重+地下水+ 爆破振动力）和荷载组合Ⅲ（自重+地下水+地震力） 下均远大于设计安全系数（图2~图4），且存在较大的优化空间。

3.4 强度折减法计算结果分析

本次计算采用Flac3D有限差分程序进行，为消除边界效应影响，根据最后划定的计算剖面区域，取x、z轴的计算范围为1106 m×463 m；x轴正向为指向边坡外，z轴竖直向上；底部仅固定z方向位移，垂直于 x、y 轴的左右两端面采用法向约束。首先在 AutoCAD 中面域化后生成 DXF文件，导入犀牛软件后，利用 griddle 插件进行网格划分，然后输出为可供 Flac3D 软件兼容的文件格式。最终在 Flac3D 中生成 1-1′剖面计算模型（图5），共划分网格单元 18422个，节点5716个。

a—不平衡推力法-2. 052；b—M-P法-1.979

a—不平衡推力法-1.956；b—M-P法-1.931

a—不平衡推力法-1.887；b—M-P法-1.878

（1）水平位移分析

对比各工况下的水平方向位移云图，可以得出在各工况下，边坡指向坡外的水平位移并未出现明显的较大位移，由小到大分别为工况Ⅰ为 3.41 cm、工况II为4.46 cm、工况Ⅲ为5. 08 cm（图6），表明该边坡在3种工况下均处于稳定状态。

a—原始状态（开挖前）；b—开挖后（荷载组合（I 自重+地下水））；c—荷载组合II（自重+地下水+爆破振动力）；d—荷载组合III（自重+地下水+地震力）

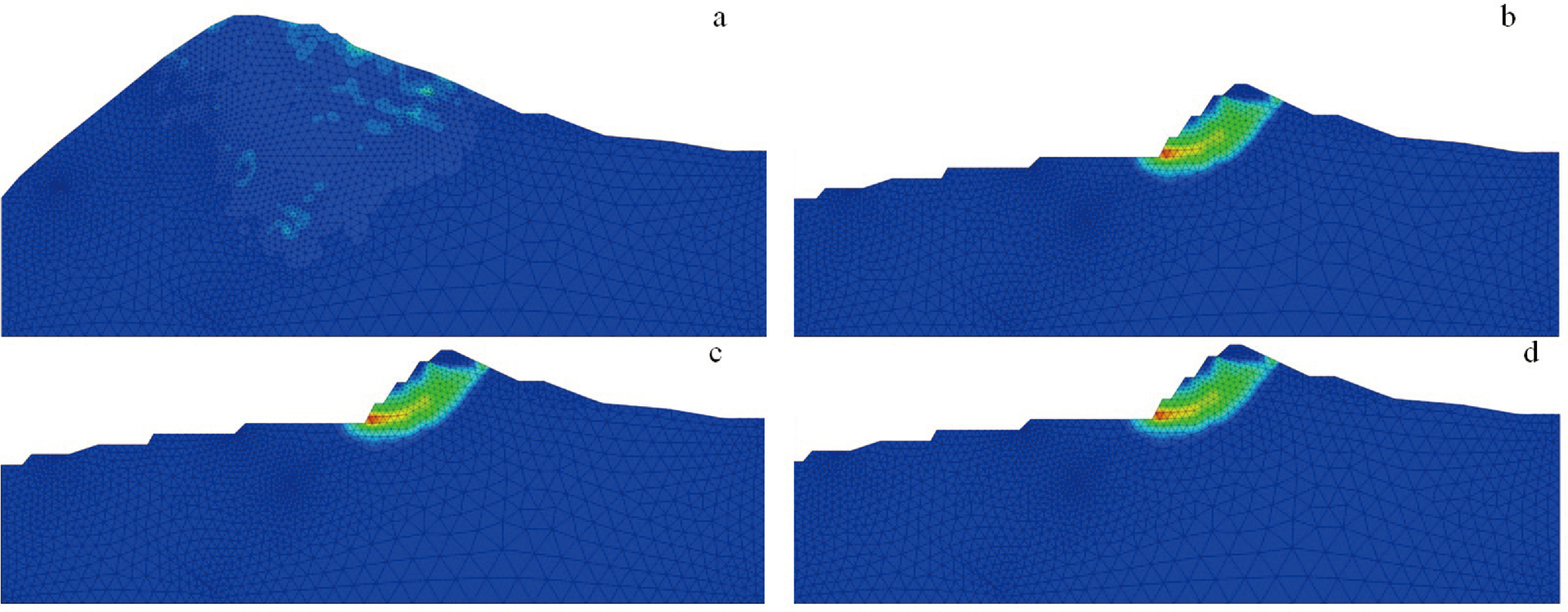
（2）塑性剪应变及安全系数分析

根据塑性剪应变云图可以看出（图7），边坡开挖后，在计算至平衡时尚处稳定状态，在强度折减法直致发生破坏时，已形成明显的剪入剪出口，潜在滑动面的位置与极限平衡计算基本一致，最终计算安全系数为：工况 I—2.789，工况Ⅱ—2.633，工况Ⅲ—2.570。

a—原始状态（开挖前）；b—开挖后（荷载组合（I 自重+地下水））；c—荷载组合II（自重+地下水+爆破振动力）；d—荷载组合III（自重+地下水+地震力）

4 结论

本文采用极限平衡法中不平衡推力法和 M-P 法，以及强度折减法，求解了西部高寒高海拔地区某矿山设计边坡在各工况下的安全系数，以及在露天采场开挖、爆破振动、地震等荷载作用下的变形情况，主要结论如下：

（1）不同荷载工况下（自重+地下水、自重+爆破振动+地下水、自重+地震+地下水），采用两种极限平衡算法时，设计边坡计算安全系数均满足现行规范要求。

（2）采用强度折减法时，得到的潜在滑动面位置与极限平衡法基本一致，且计算安全系数处于同一水平，验证了计算结果的可靠性。

（3）设计边坡所在位置在初始平衡—边坡开挖 —施加爆破或地震荷载的整个过程中，仅在初始状态到边坡开挖时，开挖体临近区域产生卸荷作用，出现边坡位移方向转变。在其他荷载施加过程中，水平位移分布规律基本一致。在仅施加荷载至计算收敛时，产生的水平位移数值均较小，而在后续强度折减过程中，由于强度参数的不断迭代折减，最终形成的连贯剪切滑移面。

参考文献