0 引言

地质灾害易发性评价是地质灾害排查、风险性调查评价及预警预报工作的基础（贺俊等，2022；张文俊等，2023）。其成果分区图不仅可作为地质灾害危险区划图、区域预警预报区划图绘制的基础性图件，还可以作为建设工程是否进行地质灾害危险性评估工作的依据图件。因此，进行区域地质灾害易发性评价研究显得尤为重要，逐渐成为研究的重点与热点问题（苏晨旭等，2019）。

前人针对地质灾害易发性评价已经做了大量的研究工作，主要聚焦以下3方面：①评价因子的遴选与分析（王小东等，2022）；②评价单元的选取与划分（丁丽等，2023）；③评价模型的建立（Pham et al.， 2020）。针对评价因子的遴选与分析，李利峰等 （2020）从评价因子的相关性角度出发，在遵循评价因子客观存在性、显著性与继承性原则的基础上，选取高程、坡度、坡向、曲率、断层、水系、道路、 NDVI、降雨量 9 种评价因子，并采用 pearson 相关系数法对山阳县滑坡影响因子进行相关性分析研究，研究结果表明各评价因子间不存在强相关性，因子间相互独立，可以作为模型建立的评价指标。王念秦等（2021）在选取坡度指标的基础上，将地形起伏度指标作为评价因子，采用Pearson相关系数法重点分析了两者之间的相关性，发现地形起伏度与坡度存在强相关性，建议在指标选取上避免重复选取。田凡凡等（2021）从评价因子的权重角度研究，采用主成分分析法对丹凤县滑坡 14 种评价因子的权重进行排序，剔除权重较小的4种评价因子，并对其余 10种评价因子做相关性分析，剔除 3类强相关性因子，仅采用剩余7种评价因子建立评价模型，取得较好的预测结果。针对评价单元的选取与划分，孙翊翔等（2022）考虑到地质灾害与斜坡的整体性、与地质环境条件的紧密联系性等，采用斜坡单元为基本评价单元，对略阳县地质灾害易发性进行评价研究。皆红富和杨晓玲（2016）、唐川和马国超（2015） 采用能够有效表现出小区域综合地貌特性的不规则地貌单元对小区域地质灾害易发性评价开展研究，并取得较好的预测结果。张利芹等（2020）采用规则的栅格单元为最小评价单元，对三峡库区的地质灾害易发性进行评价，也取得较好的评价结果。针对评价模型的建立，从模型原理上划分，主要分为传统二元统计模型、机器学习模型两大类；从模型的架构划分，分为单一模型与耦合模型两类。 Akbar and Ha（2011）从传统二元统计单一模型角度出发，采用信息量定量评价方法对巴基斯坦东北部山区滑坡易发性进行研究，研究结果发现，滑坡主要分布在极高—高易发区内，极低—低易发区内未有滑坡分布。莫运松等（2023）、江思义等（2021）则采用专家-层次分析法半定性方法分别对广西富川瑶族自治县地质灾害风险性与广西平桂区岩溶地面塌陷易发性进行评价，评价均得到较好的预测结果。传统二元统计方法主观性较强，缺乏客观数据分析，机器学习方法能够减少样本数据人为的干扰，做到更加客观的评价目的。Chen et al.（2018） 分别采用最佳优先决策树、随机森林和朴素贝叶斯树3种学习算法对中国龙海地区滑坡灾害易发性进行评价，并采用 ROC 曲线比较了 3种模型的性能优越性。谢维安等（2023）将二元统计算法与机器学习法相结合，解决了评价模型过分依赖主观性或客观性的问题，同时将信息量模型分别与逻辑回归模型、随机森林、BP 神经网络、卷积神经网络进行耦合，对金秀县滑坡灾害易发性进行评价，认为信息量与BP神经网络耦合模型预测精度最高。

虽然前人开展了一定的研究工作，但仍存在以下不足之处：用于构建模型的样本数据的纯度并未被重视或考虑在内，个别的样本异常点作为噪声点用于建构预测模型，这样会导致模型的预测精度差，一定程度上可能出现预测结果失真的现象。针对以上不足，本文采用 K-means算法、FCM 算法、层次聚类算法、DBSCAN 密度算法 4 种聚类算法对样本数据进行预处理，剔除样本中隐藏的噪声点，提高样本纯度，构建更为精准的预测模型，并以城固县为例，开展相应地质灾害易发性评价。

1 聚类算法与评价模型简介

1.1 聚类算法基本原理

聚类算法就是根据多个指标进行数学分类的一种多元统计方法，属于非监督分类算法（何静等， 2020）。聚类分析是将物理的或者抽象的数据集合划分为多个类别的过程，聚类之后的每个类别中任意两个数据样本间具有较高的相似度，而不同类别的数据样本之间具有较低的相似度，常见的聚类算法主要有 K-means算法、FCM 算法、层次聚类算法、 DBSCAN 密度算法，下面针对 4 种聚类算法原理做简单介绍。

（1）K-means算法

K-means 算法就是将 n 个样本点进行聚类分析，得到K个类别，使得每个样本点到聚类中心的距离最小（刘铁铭等，2023）。其算法过程可以概括为以下 4 个步骤：①从样本中选择 K 个对象作为初始聚类中心；②计算每个聚类样本对象到聚类中心的距离，将距离聚类中心最近的样本对象分为1簇，共形成K个簇；③再次计算每个聚类中心；④重复步骤 ②～③，直到达到最大迭代次数，结束计算。

（2）模糊 C 均值聚类（Fuzzy C-means，简称FCM）算法

FCM 算法是一种基于模糊逻辑的聚类方法，旨在将样本点分配到预定义的群集中，以实现样本点之间的相似性最大化和不同群集之间的差异最大化（董世鹏和吴韶波，2023）。其算法过程可以概括为以下 5个步骤：①设定聚类数目 C和参数 m；②给出初始隶属度矩阵 U^（0） （U^（0） 各列元素之和为 1）；③ 计算新的聚类中心V_j；④计算新的隶属度矩阵；⑤用一个矩阵范数比较两次迭代之间隶属度矩阵，如果其值小于或等于e，则停止迭代。

（3）层次聚类算法

层次聚类算法是通过计算不同类别样本点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中，不同类别的原始数据点是数的最底层，树的顶层是一个聚类的根节点（王欣，2016）。其算法过程可以概括为以下 4 个步骤：①将样本集中的每个样本点当作一个类别；②计算所有样本点之间的两两距离，并从中挑选出最小距离的两个点构成一个簇；③继续计算剩余样本点之间的两两距离和点与簇之间的距离，然后将最小距离的点或簇合并到一起；④重复步骤②～③，直到满足聚类的个数或其他设定的条件，便结束算法的运行。

（4）DBSCAN密度算法

DBSCAN 密度算法，全称 Density-Based Spatial Clustering of Applications with Noise，是一种基于密度的空间的数据聚类方法（王军和高建杰，2023）。其算法过程可以概括为以下 2 个步骤：①计算每个样本点以 r 为半径圆域内的样本点，并得到相应的核心样本点；②依次遍历每个样本，根据其是否为核心样本对直接可达的样本点进行簇类别的划分。

各聚类算法的优缺点如表1所示。

1.2 熵指数（Index of Entropy，简称 IOE） 模型基本原理

熵指数模型是一种用来衡量系统的不稳定性、无序性、不平衡性程度的二元统计分析方法。它是一种客观赋权法，通过分析每个输入变量来确定其权重值。相较于主观赋权法，熵指数模型能一定程度减少主观因素的干扰，结果更具客观性，可信度和精确度均较高。地质灾害的熵是指各种诱发因子对地质灾害发育的影响程度。熵值越小，不确定性越大，反之亦然。因此，在地质灾害易发性评价中，熵值可以用来计算诱发因素的客观权重。具体计算步骤如下：

式（1）、（2）中：a 表示诱发因素二级因子分级中，未发生地质灾害所占面积与整个研究区内未发生地质灾害总面积的比值；b 表示诱发因素二级因子分级中，发生地质灾害所占面积与整个研究区内地质灾害总面积的比值；FR_ij表示由 b／a 确定计算出的概率比率值，可作为二级因子分级的量化取值；P_ij表示频率密度。

式（3）、（4）中：H_j和H_jmax表示熵值；S_j表示二级因子分级数；H_jmax由 Sj取对数得到。

式（5）～（7）中：I_j表示诱发因素信息率；W_j表示诱发因素一级指标权重。

1.3 信息量（Information Value，简称IV）模型基本原理

信息量法是以信息论为基础的统计方法，最初用于地学上的矿产资源勘查方面，近年来被用于地质灾害领域（李怡静等，2021）。此方法通过计算各诱发因素对地质灾害所提供的信息量值来综合衡量地质灾害发生的可能性。诱发因素所提供的信息量值越大，表示地质灾害发生的可能性越大，正值表示促进地质灾害的发生，负值表示抑制地质灾害的发生，0 值表示对地质灾害发生未有影响。信息量模型具体实现过程如下：

式（8）中：N_i表示诱发因素二级因子x_i内的地质灾害数量；N表示研究区地质灾害总数；S_i表示诱发因素二级因子x_i所占面积或栅格数；S表示研究区总面积或栅格总数，IV_i表示诱发因素二级因子信息量值。

1.4 IOE-IV耦合模型基本原理

通过IOE模型计算得到的诱发因素一级指标权重 W_j与 IV 模型计算所得诱发因素二级指标信息量值（相对权重值）相乘，建立 IOE-IV 耦合模型，具体计算公式如下：

式（9）中：W_i表示诱发因素综合权重值。

2 研究区概况

城固县位于陕西省汉中市中部，地理位置东经 107°20'00″，北纬 33°09'24″，总面积约 2211.32 km²，海拔 412～2397 m，属于汉中盆地的一部分。县域南北狭长，地势南北高，中间低。地貌由县域南北向中部依次为中山区、低山丘陵区与冲积平原区。城固县属北亚热带湿润季风区，区内气候温暖湿润，具有冬无严寒，夏无酷暑，雨量充沛，四季湿润，雨热同季，干湿交替的特点，多年平均气温 114.2℃，多年降水总量平均约 800 mm（曹虎生等， 2015），日最大降雨量 103.8 mm（1987 年 8 月 3 日）。区内水系属长江流域汉江水系，主要河流有湑水河、文川河、南沙河、堰沟河等。境内地层出露较全，最老地层为中生代及元古宙，最新地层为第四系更新统。境内褶皱、断裂构造发育，主要褶皱有秦岭褶皱系的南秦岭印支褶皱带、康县—略阳海西褶皱带及扬子准地台北缘的龙门—大巴台缘褶皱带等。区域性断裂主要以马道—双溪断裂带、阳平关—洋县断裂、海棠寺—七里店断裂、峡口—白勉峡断裂带为主（曹虎生等，2013^①），其中马道—双溪断裂带于早古生代已明显存在，华力西期、印支期和燕山期均有明显活动；阳平关—洋县断裂带于中元古代已有运动，但主要集中在晚元古代和早古生代，之后各个构造时期均有活动；海棠寺—七里店断裂为汉中断凹南缘断裂；峡口—白勉峡断裂带为汉南凸起台阶式断裂带，控制震旦纪以来的盖层沉积。依据城固县地质灾害详细调查报告统计（2013 年度），域内在册地质灾害点数为 126 处，其中滑坡 117处，崩塌9处，以堆积层与黏性土滑坡为主，岩质滑坡仅有2处。研究区地理位置与地质灾害点空间分布如图1所示。

3 样本数据处理

3.1 数据来源及评价单元划分

本文采用的 ASTER GDEM 30 m 分辨率数字高程模型（DEM）与 Landsat8 OLI_TIRS 卫星数字产品通过国家地理空间数据云网站下载；所采用的基础地质数据来源于陕西省城固县1∶5万地质灾害详细调查报告等基础资料，部分野外照片见图2、图3所示。地质灾害点来源于城固县在册地质灾害数据库。

本文以30 m×30 m的栅格单元作为最小评价单元，将研究区共划分为2457024个规则栅格，面积约 2211.32 km² 。

3.2 评价指标选取

在遵循评价因子客观存在性、显著性与继承性原则的基础上，通过分析城固县孕灾地质环境条件、灾害发育特征、分布规律等，综合选取气象水文类（水系、年降雨量、地形湿度指数）、地形地貌类 （高程、坡度、坡向、曲率、地形起伏度、地面粗糙度）、基础地质类（地层岩性、断层）、植被覆盖类（归一化植被指数 NDVI）4 类 12 种诱发因素为评价指标。通过ArcGIS 10.2操作平台，将各类数据源通过 ArcGIS工具箱工具进行不同操作处理，提取12种评价因子图层，并将地质灾害点叠加至各图层，提取地质灾害点样本属性数据，各叠加图层如图4所示。为消除样本特征属性间不同量纲间的差异性，采用 Z-score 标准化法对样本数据作归一化处理。归一化处理公式为：

式（10）中：x为样本数据；u为样本均值；σ为样本标准差。

3.3 样本数据聚类分析

本文采用MATLAB 2020a工程软件聚类算法包实现样本数据聚类分析，将 126 处归一化样本数据输入软件算法包，运行得到表2 聚类结果。

由表2 聚类结果分析可知：针对同一样本数据集，4 种聚类算法的聚类结果均不相同。K-means 算法、FCM 算法、层次聚类算法、DBSCAN 密度算法遴选出的噪声点数分别为 11 个、7 个、13 个与 9 个，这些噪声点之间存在以下包含关系：｛层次聚类算法⊇ K-means 算法⊇ DBSCAN 密度算法 ⊇ FCM 算法｝。层次聚类算法与 K-means 算法对样本噪声点的敏感性最强，而 FCM 算法、DBSCAN 密度算法则相对较弱。对 4 种聚类结果取并集，即取层次聚类算法的聚类结果，得到样本噪声点为 13 个，有效样本点为113 个，样本纯度为89.68%。

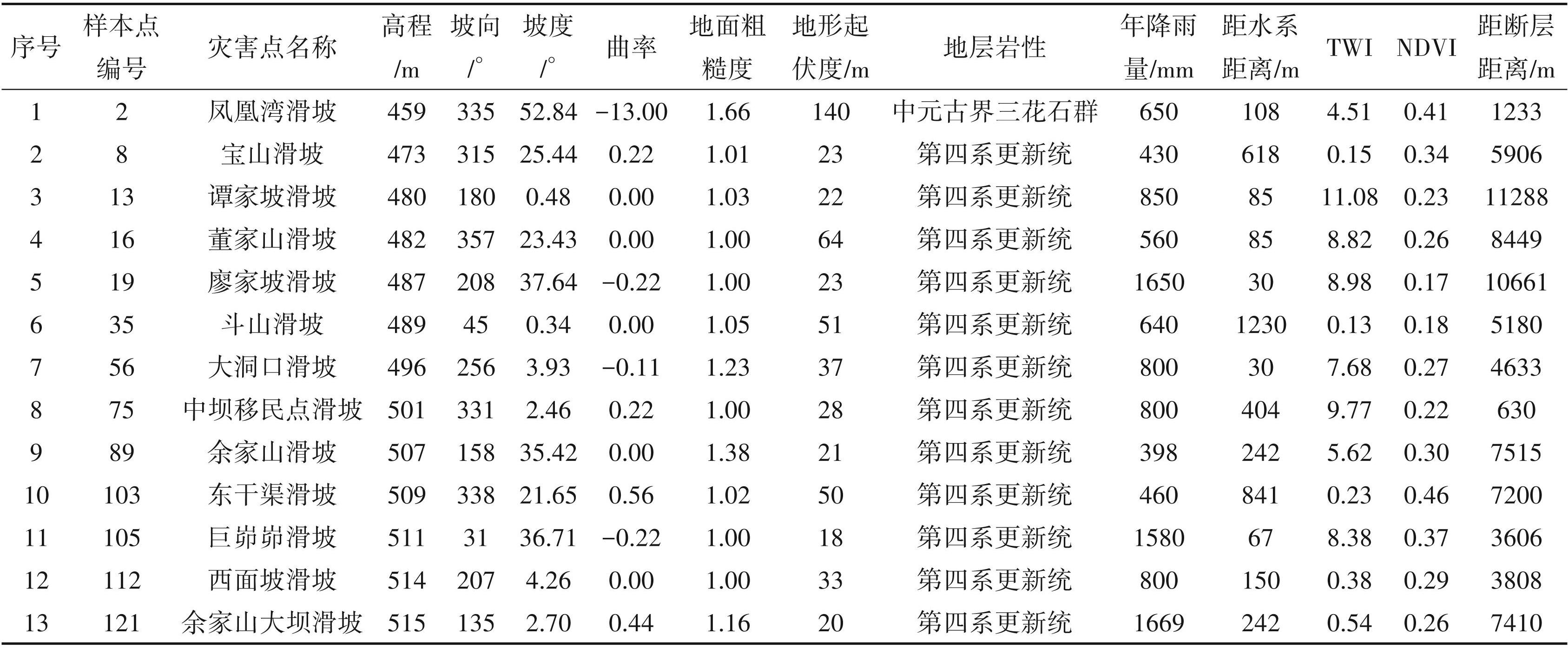
提取13处样本噪声点特征属性值（表3）。从统计学角度分析发现，样本编号 13，35，56，75，112， 121坡度均小于10°，与剩余样本点坡度数据对照可知，此6个样本点坡度数据明显异常。此外，根据滑坡、崩塌坡度统计文献（徐永年等，1999；郭果等， 2013）发现：滑坡发生需满足一定的坡度条件，坡度一般在 20°～45°间最易诱发滑坡的发生，坡度小于20 °时，坡体一般处于相对稳定的状态。因此，可以判断此6个样本噪声点属于坡度异常点。编号2，8， 16，19，89，103，105，121 样本年降雨量与剩余样本点年降雨量数据相比存在较大差异，年降雨量值明显偏小，并且与县域多年降雨量等值线图存在较大差异，由此判断此 8 处样本噪声点是由年降雨量数据异常造成。

a—高程；b—坡度；c—坡向；d—曲率；e—地形起伏度；f—地面粗糙度；g—地层岩性；h—年降雨量；i—距水系距离；j—地形湿度指数；k—距断层距离；l—NDVI

4 地质灾害易发性评价

4.1 评价指标分级体系

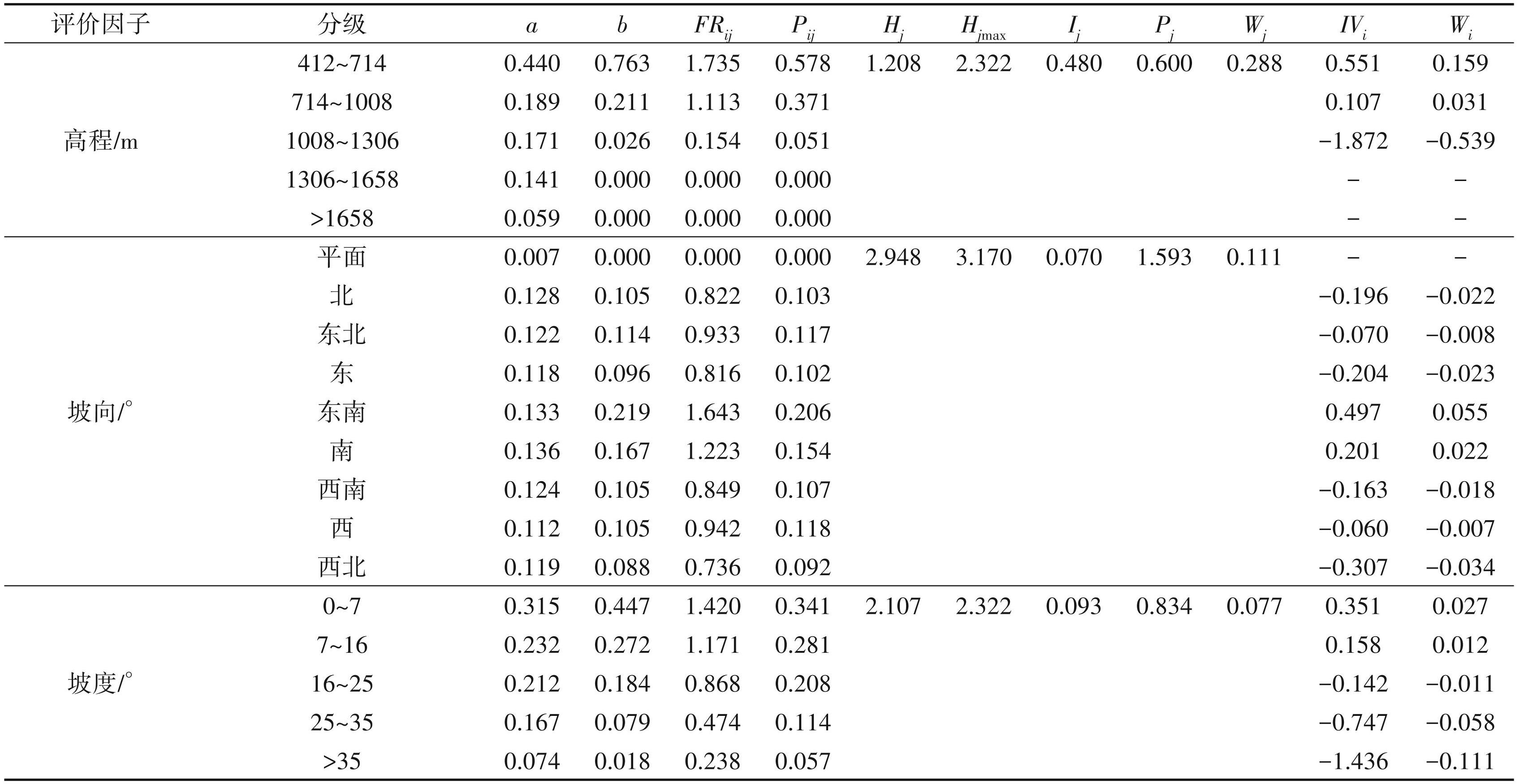
采用自然间断法对高程、坡向、坡度、曲率、地面粗糙度、地形起伏度、TWI、NDVI 8种评价因子进行分级处理，采用相等间隔法（曹春野，2023）对年降雨量、水系、断层 3 种评价因子进行分级处理，对地层岩性按地层时代进行分级处理，并将其标签化。依据以上公式（1）~（9）分别计算不同评价因子分级下的过程值与结果值，构建地质灾害易发性评价指标体系（表4）。

续表1

4.2 研究区易发性评价

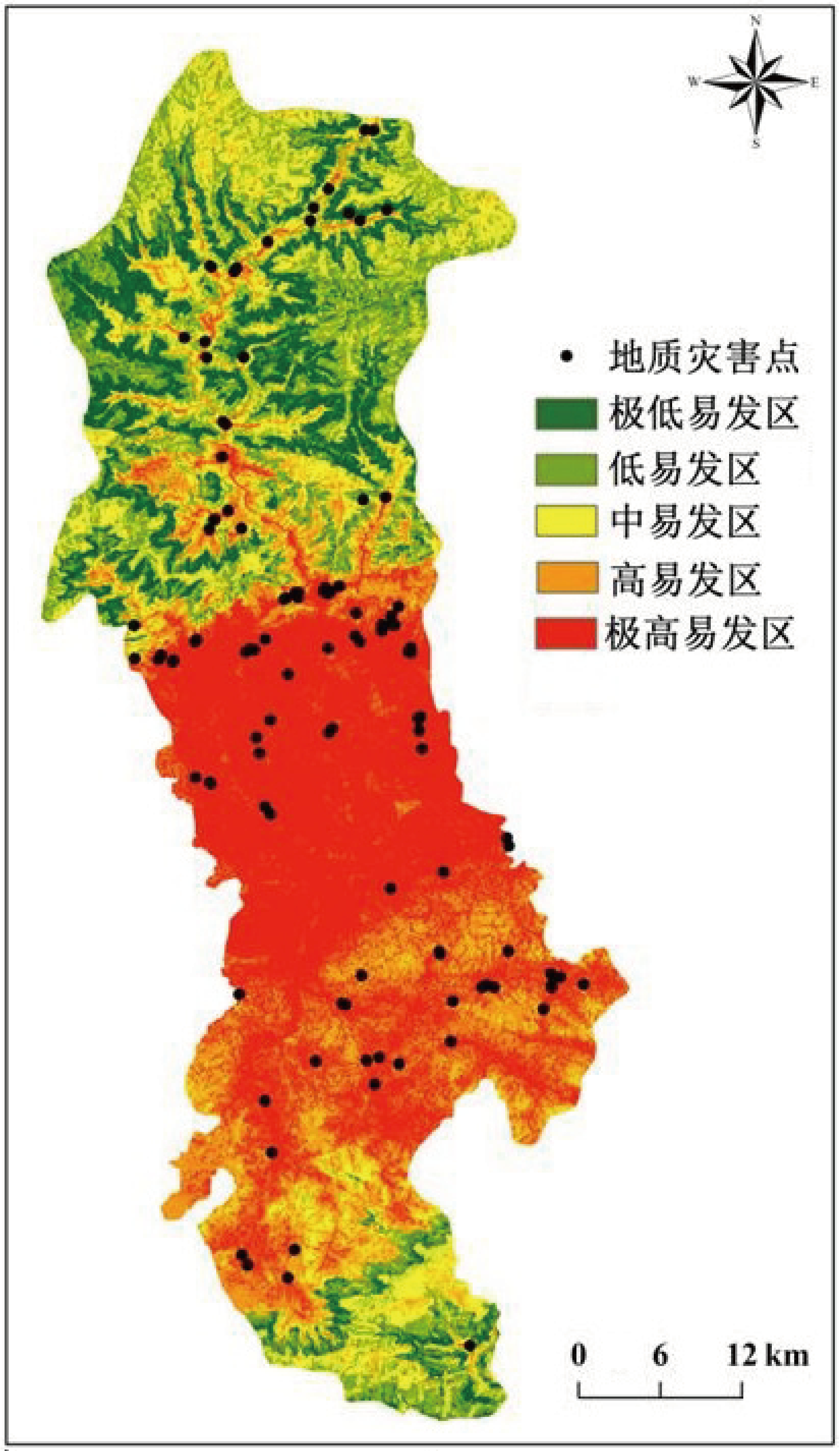
计算提纯后的各评价因子分级的综合权重 Wi，并将其进行图层叠加计算，得到城固县地质灾害易发性指数值（-1.866~0.946），将易发性指数值按照自然间断点法划分为极高易发等级（0.194~0.946）、高易发等级（-0.241~0.194）、中易发等级 （-0.241~-0.652）、低易发等级（-1. 047~-0.241）、极低易发等级（-1.866~-1. 047），生成城固县地质灾害易发性区划图（图5）。

统计各易发分区面积、灾害点数、灾害点密度等，统计结果如表5 所示。极高—高易发分区面积为 1204.87 km²，地质灾害点数为 104 个，灾害点密度达 0.152 个/km²；极低—低易发区面积为 623.22 km²，地质灾害点数仅为 4 个，灾害点密度达 0. 012 个/km²。由此结果可知，地质灾害点在极高—高易发区内分布较为集中，在极低—低易发分区分布较少较分散，预测结果较为合理准确。

从易发性区划结果分析可知，在第四系更新统地层内，地质灾害易发等级主要为极高—高易发，地质灾害呈面状分布，在其它地层内，地质灾害均有少量分布，且随机发育，受地层控制作用不明显； 从高程角度分析，极高—高易发等级主要分布在高程412~500 m范围内，且地质灾害发育呈线状分布，在其他高程段内，地质灾害不甚发育；从水系角度分析，极高—高易发等级主要分布在距水系 500 m 范围内，随着距离的增加，易发等级降低，地质灾害数量也随之变少。该研究可以为地质灾害易发性评价样本优化、模型选择提供一定的理论依据。

5 结论

（1）基于 K-means 算法、FCM 算法、层次聚类算法、DBSCAN 密度算法 4 种聚类算法所得的样本噪声点为 13 个，有效样本点数为 113 个，样本纯度为 89.68%。

（2）将熵指数（IOE）模型与信息量（IV）模型进行耦合，构建 OIE-IV 耦合模型，开展区内地质灾害易发性评价，评价结果表明：极高—高易发区灾害点密度达 0.152 个/km²，地质灾害点在极高—高易发区内分布较为集中，预测结果较为合理准确。

（3）极高—高易发等级主要分布在高程 412~500 m、距水系 500 m 范围内，地质灾害主要受人类工程活动与河流冲刷切割的影响作用较强，部分野外验证照片见图6、图7所示。

注释

① 曹虎生，蒋泽泉，王建华.2013. 陕西省城固县地质灾害详细调查报告[R]. 汉中：陕西省地质调查院.

参考文献