-
0 引言
-
滑坡灾害在露天金属矿山中是一项影响安全开采的主要挑战。边坡的变形、破坏和失稳过程属于一个复杂的系统,其复杂性源于构成边坡的岩土体材料的多样性和内部结构的复杂性,这导致了边坡通常呈现出多种不同的破坏模式。边坡稳定性分析与评价的研究内容涵盖了岩土体材料的力学性质、地质构造特征、地表形态、降雨和地震等外部荷载条件对边坡稳定性的影响,以及边坡内部的应力、应变和变形特征等。这些内容需要借助先进的数值模拟技术、地质勘察与监测技术、地球物理勘探技术等手段进行研究与分析。边坡稳定性分析与评价的学术研究旨在深入理解边坡破坏机制、预测滑坡灾害的发生概率与规模,从而为露天金属矿山的安全开采提供科学依据和技术支持。
-
近年来,有限元强度折减法在露天矿边坡稳定性分析领域得到了广泛的应用与研究。在露天矿开采中,边坡稳定性是一个至关重要的问题,直接关系到矿山生产的安全与效率。有限元强度折减法作为一种高效、准确的数值模拟方法,已经成为露天矿边坡稳定性分析的主要工具之一。强度折减法的起源是以数值分析理论为基础的,发展至今也取得了较好的应用效果(Zienkiewicz et al.,1975) 最先提出强度折减概念,并且认为可以将此概念应用到边坡稳定性的分析计算之中。直到 1992 年, Matsui and San(1992)采用 Zienkiewicz 的方法分析了多个边坡的稳定性,并把该方法正式命名为强度折减技术,从物理意义出发,讨论了临界强度折减系数与传统边坡稳定分析方法安全系数的关系。极大推动了强度折减的有限元边坡稳定分析方法的发展。在此之后众多学者不断在该领域进行更加深人的研究(Dawson et al.,1999;Griffiths and Lane,1999;Bai et al.,2014;Deng et al.,2016)。
-
国内学者赵尚毅等(2001)结合实际工程,用折减法分析了锚杆对边坡的加固效果。张鲁渝等 (2003)通过对上百个边坡稳定算例进行分析,得出折减法的计算结果与 Bishop 法相比误差离散程度非常低,表明了有限元折减法良好的适用性。孙伟 (2003)用有限元强度折减法对边坡不同状态下的安全系数与坡体所对应的形变状况进行了分析,并对其在工程中的适用性提出了评价。唐芬和郑颖人(2009)认为边坡的破坏是一个渐进积累破坏的过程,提出了双折减系数法。
-
与传统的极限平衡法相比,强度折减法更有优势,能考虑边坡体的应力、本构关系、变形、开挖和支护结构的作用效应等(郑宏等,2002;郑颖人和赵尚毅,2004;郏建磊,2007;杨光华等,2009;徐炎兵和王新志,2012;李小春等,2014)。由于各种因素,现在工程中遇到的大部分边坡无法确定其准确的滑移面。强度折减法在计算时不需任何假定,能自动求得任意形状的临界滑动面及相对应的最小安全系数,且适用于具有复杂地貌、地质的边坡,能够很好解决这一难点。同时,强度折减法还可以反映坡体失稳及塑性区的开展过程,能够模拟土体与支护结构的共同作用,能够为工程治理提供更准确的理论依据(王广月等,2005;雷远见和王水林,2006; 欧湘萍等,2009;陈国庆等,2013;付正道,2014;蒋明镜等,2019;曾凯波等,2020)。随着计算机技术的发展,强度折减法也在不断进行改进,适用工程范围将更加广阔,能够更准确可靠地模拟更多工程。
-
综上所述,强度折减法具有相当多的优点和可靠性,本文通过有限元强度折减法进行鹿鸣钼矿边坡稳定性分析,能够为矿山的安全管理和生产决策提供重要的技术支持。同时,对于边坡稳定性的深入理解也有助于优化开采方案,减少生产过程中的安全隐患,提高矿山的经济效益和可持续发展能力。
-
1 鹿鸣采区概况及边坡分区
-
1.1 鹿鸣采区概况
-
节理岩质边坡是指由节理岩构成的边坡,其稳定性和性质受到岩石节理的影响。岩石节理是岩石内部的裂隙或断裂,通常形成于岩石形成过程中的地质作用,如岩层沉积、构造变形等。这些节理对岩体的力学性质、水文地质特性以及边坡稳定性都有着重要影响。节理岩质边坡主要存在以下特殊性。
-
节理岩体的节理分布通常不均匀,内部常常存在多种不同倾向和倾角的节理,这种非均质性使得岩体的力学性质在不同方向上有明显的差异。不同节理参数的节理面对岩体的强度影响程度不同,导致岩体的强度分布存在畸变。地下水通过节理的流动和压力变化可能引发边坡的变形和破坏。此外,节理岩体边坡的失稳机制通常比较复杂,不仅受到岩体内部的力学性质影响,还受到外部荷载、水文地质条件等因素的综合作用。
-
如图1 所示,鹿鸣钼矿北帮及东北帮受区域动力作用的影响,边坡岩体节理裂隙发育,存在3组优势结构面,当在滑面出露时,可能发生沿两侧结构面的楔形体破坏,不利于边坡的稳定。且其倾角偏陡,在开挖扰动过程中容易造成裂隙贯通,发生倾倒、崩塌破坏。
-
图1 北帮、东北帮节理岩质边坡
-
1.2 边坡几何特征分析
-
采用 GIS 技术,对矿山边坡几何特征(高程、坡度、坡向)等进行可视化分析,分析现状边坡要素形成原因、过程,如图2所示,通过高程可见,露天境界开采标高在565~345 m,形成的边坡高度在75~220 m。排土场最大标高535 m。
-
采场边坡的几何特征决定了其坡度范围的分布。绝大多数滑坡危险性评估都利用坡度作为几个重要的因素之一。滑坡的发生必须具有一定的启动坡度,它直接影响边坡岩体的应力分布,控制着坡体的稳定性。
-
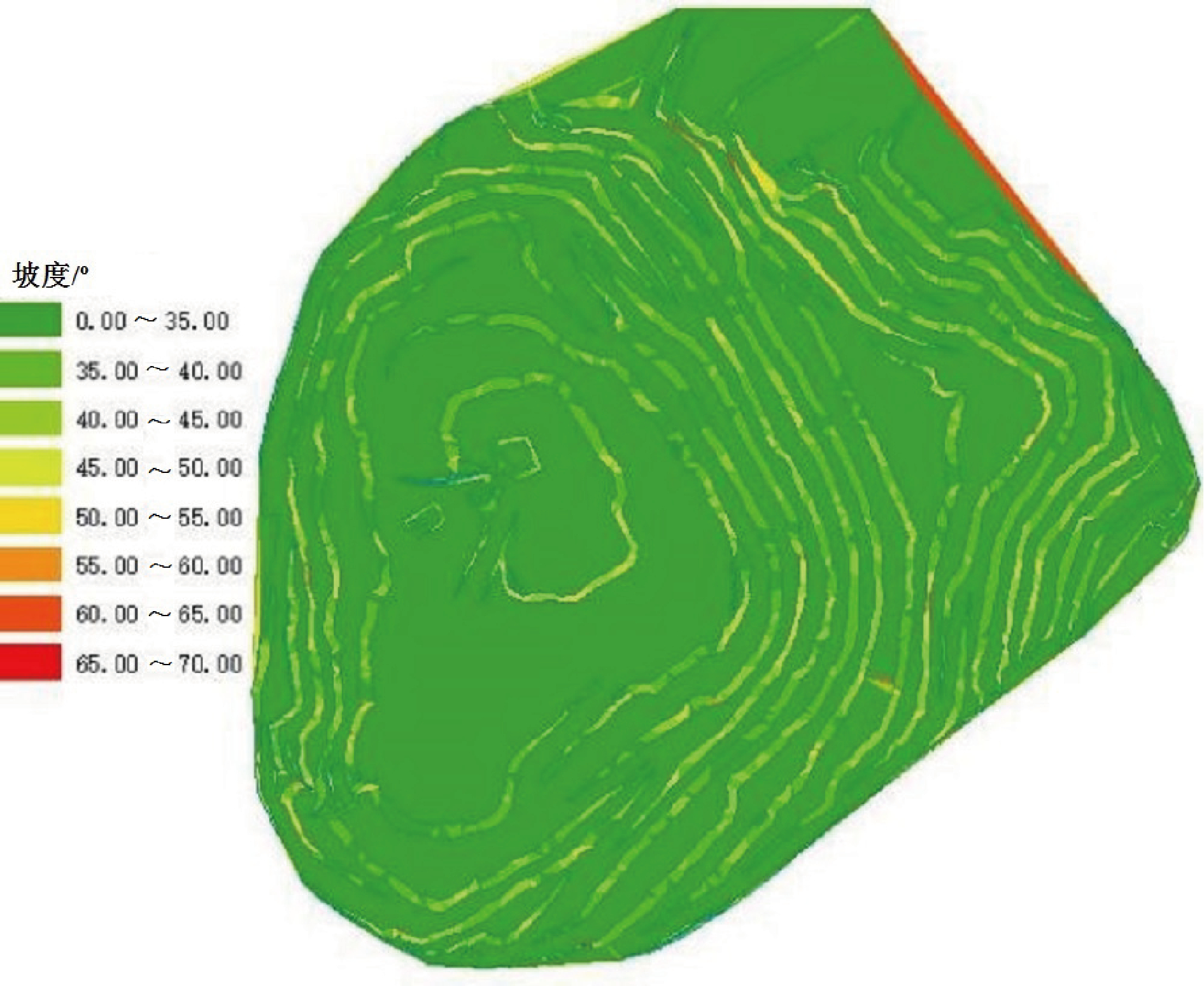
因此边坡坡度分析的主要目的是校核当前现状与露天开采境界边坡要素(此处主要是台阶坡面角)的关系。设计阶段坡面角:第四系台阶坡面角 35°,风化岩台阶坡面角 40°,西帮受 F3 断层影响基岩台阶坡面角 45°~53°,其余位置基岩台阶坡面角 65°生产时台阶坡面角为70°。
-
根据前期调查结果,北帮、东北帮主要台阶剖角度和倾向值为:从 360 平台至 450 平台共有 6 个台阶坡面,坡面坡角为36.3°~57.4°,台阶坡面T平均坡角为 45°;坡面 T1(单台阶):116°∠38.7°;坡面 T2(单台阶):116°∠38.9°;坡面 T3(单台阶):116°∠38.1°;坡面 T4(单台阶):116°∠57.4°;坡面 T5(单台阶):116°∠54.5°;坡面 T6(单台阶):116°∠36.3° (图3)。
-
图2 现状露天境界高程分析
-
图3 现状境界坡度分析
-
1.3 边坡分区
-
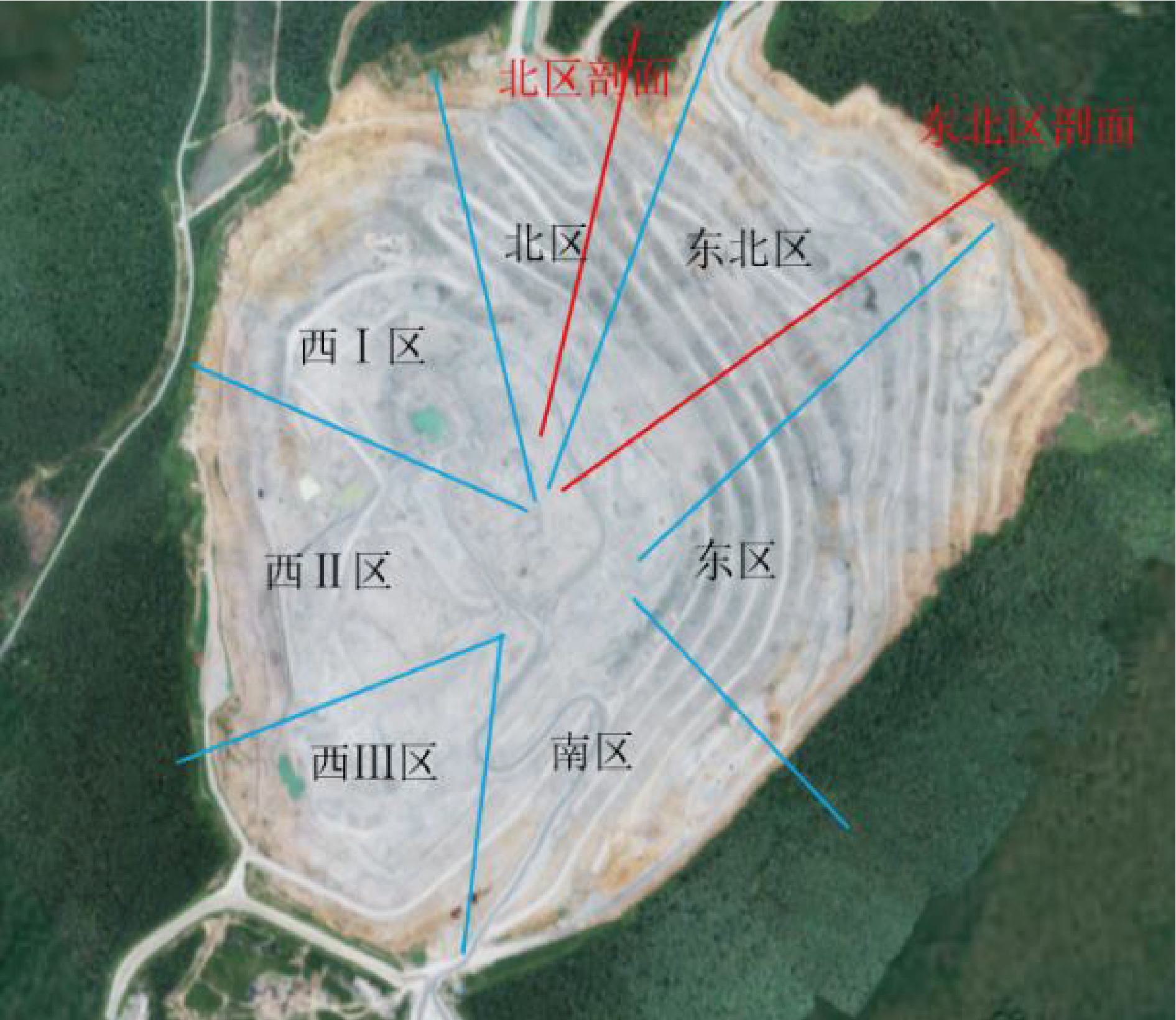
采场边帮台阶稳定性的因素除岩层性质、岩体结构类型外,还与岩体优势结构面发育程度、性质、产状与边坡面的倾向组合有关。边坡分区有利于进行边坡稳定性评价,分区原则基于工程地质条件、边坡几何形状和边坡倾向的相似性。鹿鸣采区可划分为 7 个边坡分区。本文分别在北区、东北区选取典型剖面(北区剖面、东北区剖面)进行数值分析,如图4所示。
-
图4 采场边坡分区及剖面位置图
-
2 边坡稳定性有限元强度折减法分析
-
2.1 有限元强度折减法
-
强度折减法的基本原理是将岩土体的抗剪强度 c、φ 的正切值除以折减系数 Fr,采用有限元进行计算,如果边坡在选取的折减系数下达到破坏,此时的折减系数便是安全系数。
-
如果岩土体的实际抗剪强度指标为c和φ,计算式选取的折减系数为Fr,则折减强度为:
-
则式(1)成为
-
参数 φr 和 cr 为折减后的强度指标,将 φr 和 cr 带入有限元计算,如果折减系数 Fr >1. 0,则利用有限元计算的位移和应力就比实际的大,破坏的单元也比实际的多。令 Fr从 1. 0 逐步增大,则计算的位移逐步变大,破坏单元逐步增加,当边坡整体失稳时的 Fr即为安全系数,此时的 Fr 也符合 Bishop 法的定义。
-
2.2 剖面稳定性计算
-
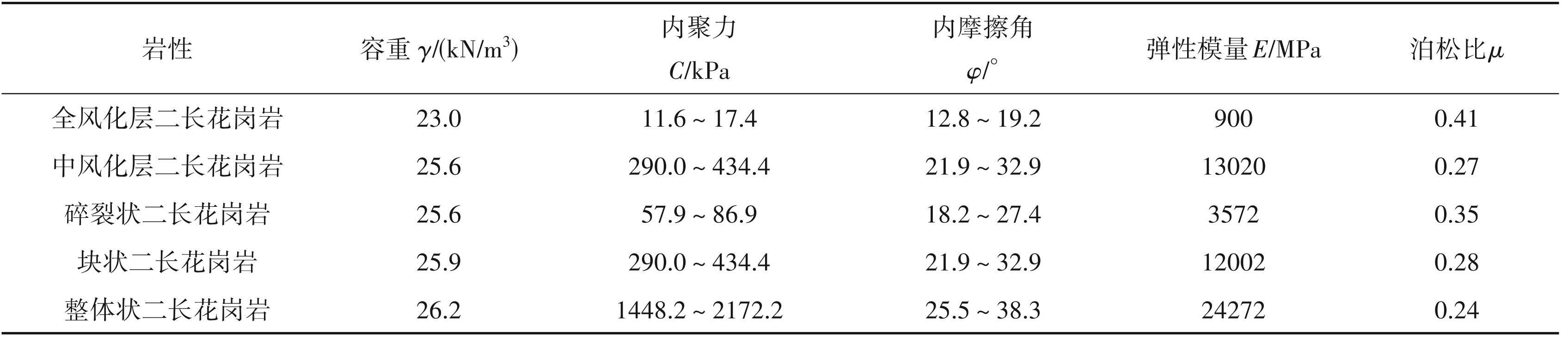
依据鹿鸣钼矿采场实际,如图4、表1所示,选取典型剖面并结合已知岩体力学参数,对北区、东北区的边坡稳定性进行验证,共选取2个典型剖面,进行数值分析模拟研究,选取边坡岩土体力学参数基于边坡尺寸的基础上建立边坡有限元模型,分析边坡在自重+地下水工况Ⅰ、自重+地下水+地震工况 Ⅱ、自重+地下水+爆破工况Ⅲ下的稳定性情况。
-
2.2.1 北区剖面
-
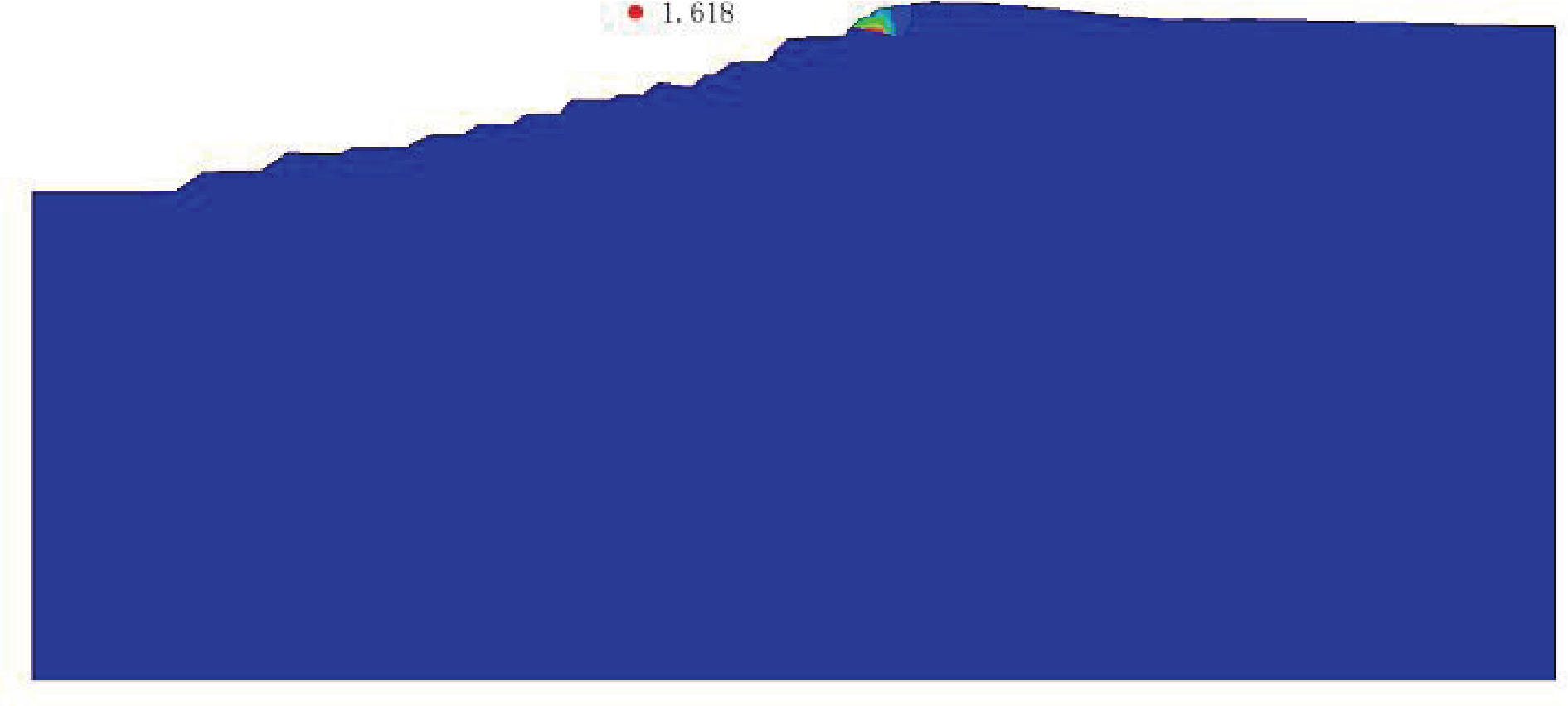
北区代表性剖面如图5 所示,剖面高度 146.3 m,边坡角度 14°,上部存在一定厚度第四系地层和风化岩层,中部结构较为完整。如图6~图8所示,剖面计算结果如下:
-
2.2.2 东北区剖面
-
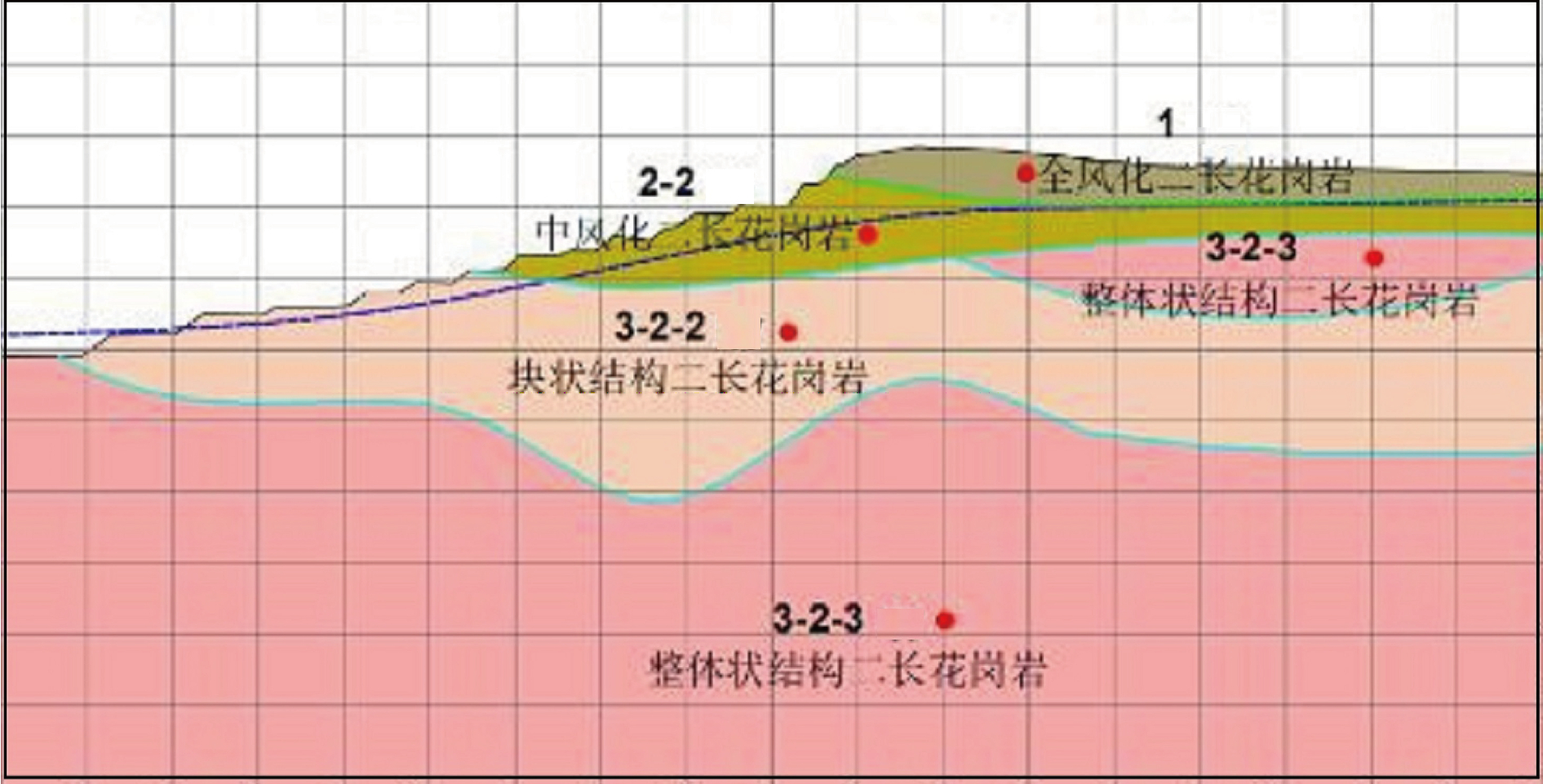
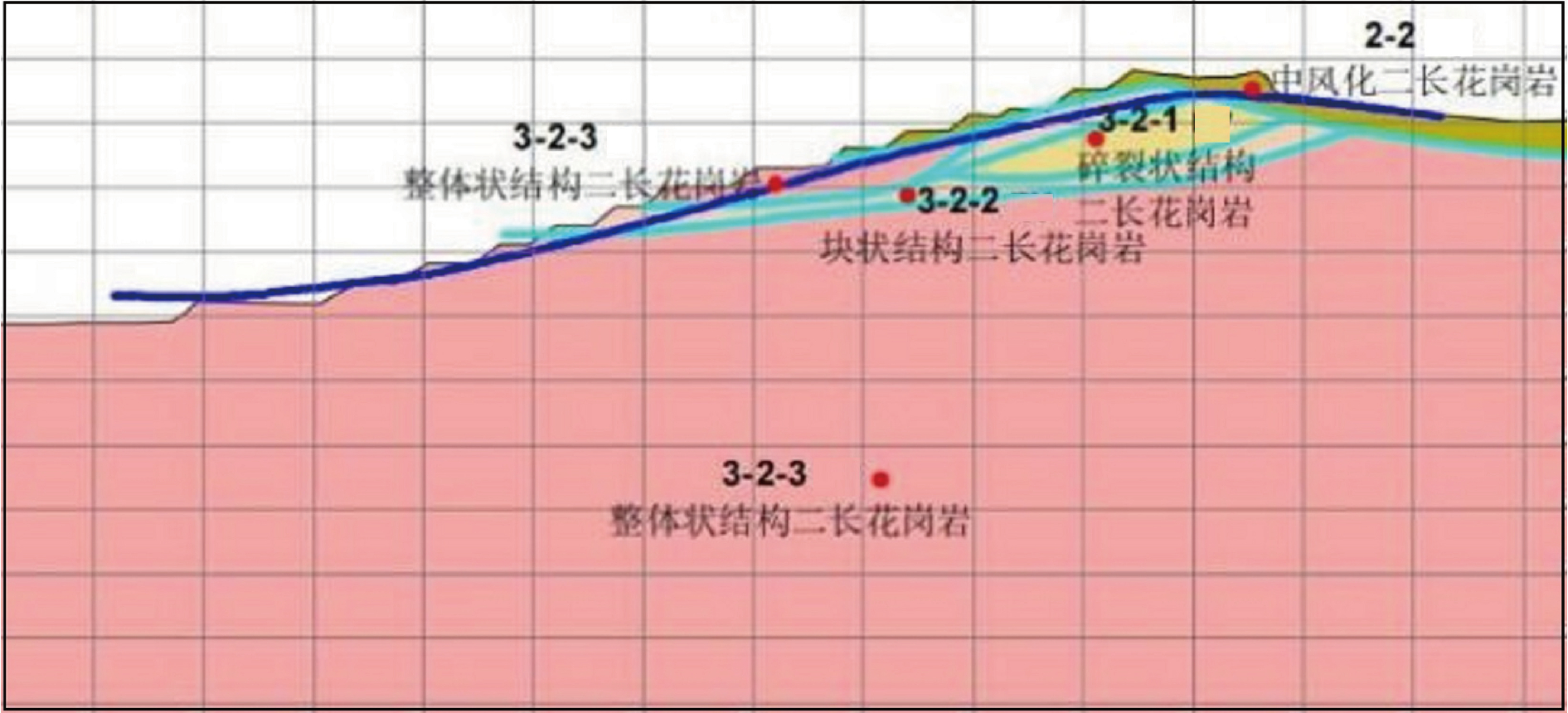
东北区代表性剖面如图9 所示,剖面高度 192.4 m,边坡角度 15°,上部存在一定厚度中风化岩层和碎裂状二长花岗岩,碎裂状、块状二长花岗岩是一种常见的火成岩,岩石中存在着大量的碎裂、裂缝和断裂,具有特定的岩石特性,包括颗粒状的结构、明显的二长矿物晶粒等。这些特性影响着岩石的力学性质、工程特性以及在地质环境中的稳定性,且对边坡局部的稳定性影响较大。如图10~图12所示,剖面计算结果如下:
-
东北区剖面的塑性应变区分布如图所示,主要集中在 3-2-1 碎裂状二长花岗岩层与 3-2-2 块状二长花岗岩层,且贯通为连续塑性滑移带,使边坡发生整体性破坏。
-
图5 北区剖面图
-
图6 北区剖面1-1工况Ⅰ计算结果
-
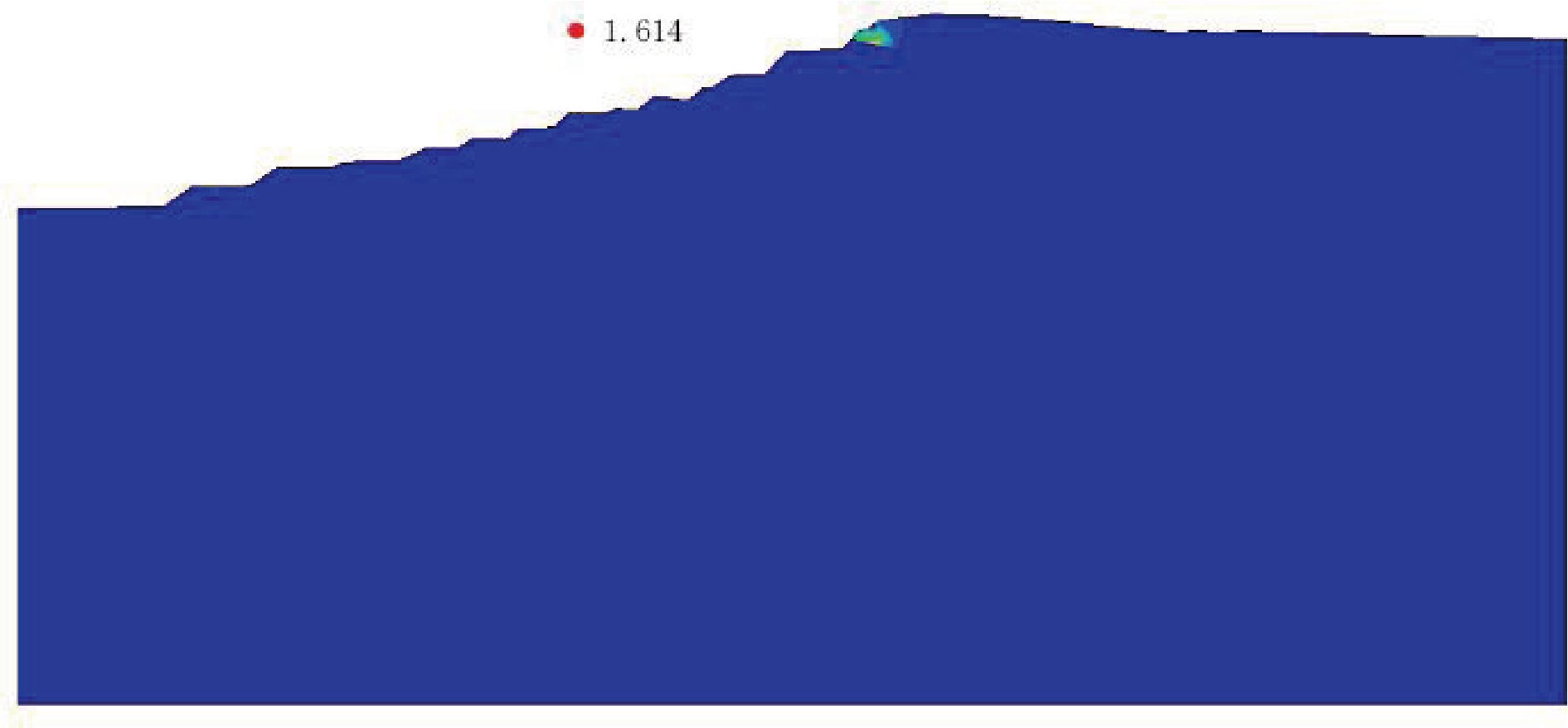
图7 北区剖面1-1工况Ⅱ计算结果
-
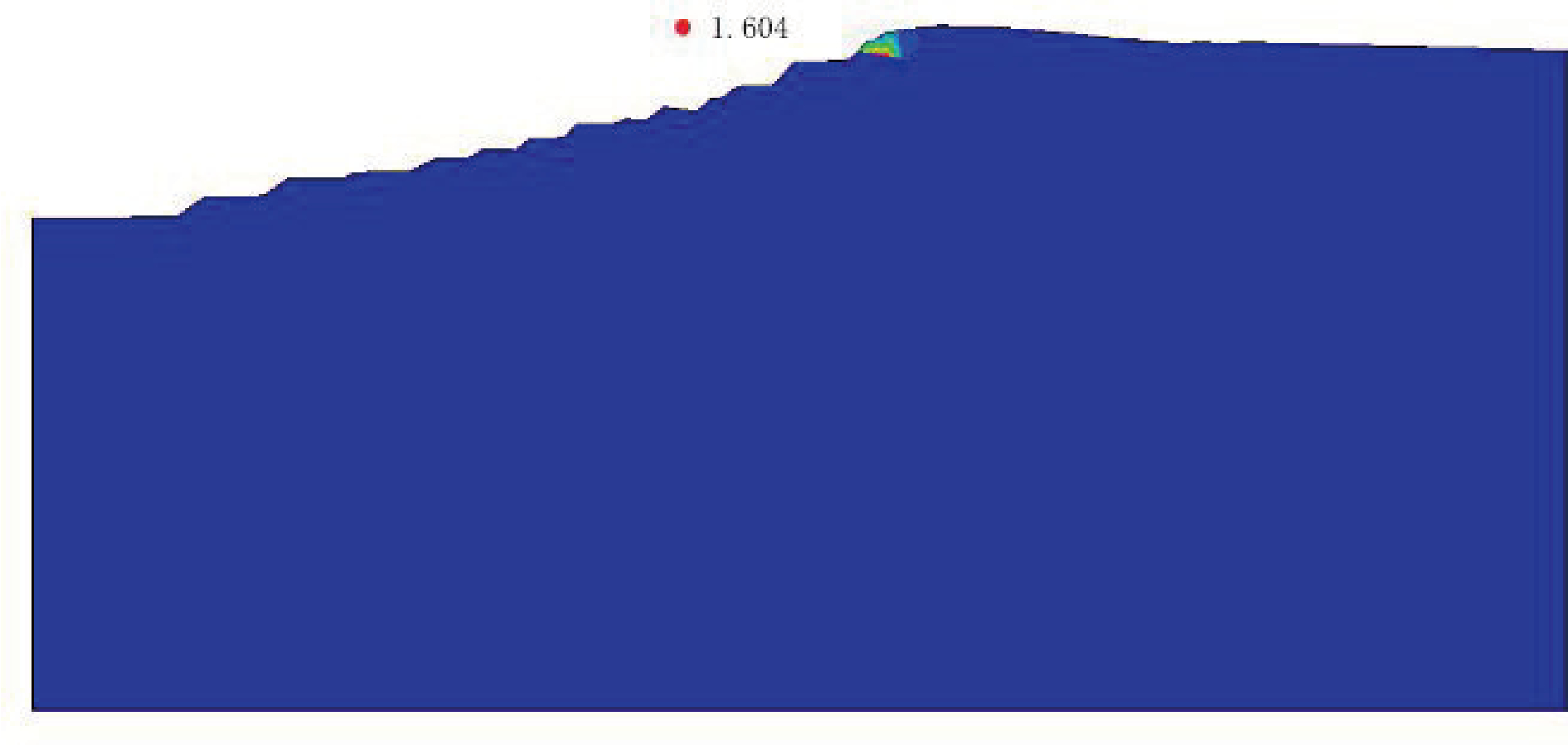
图8 北区剖面1-1工况Ⅲ计算结果
-
图9 东北区剖面图
-
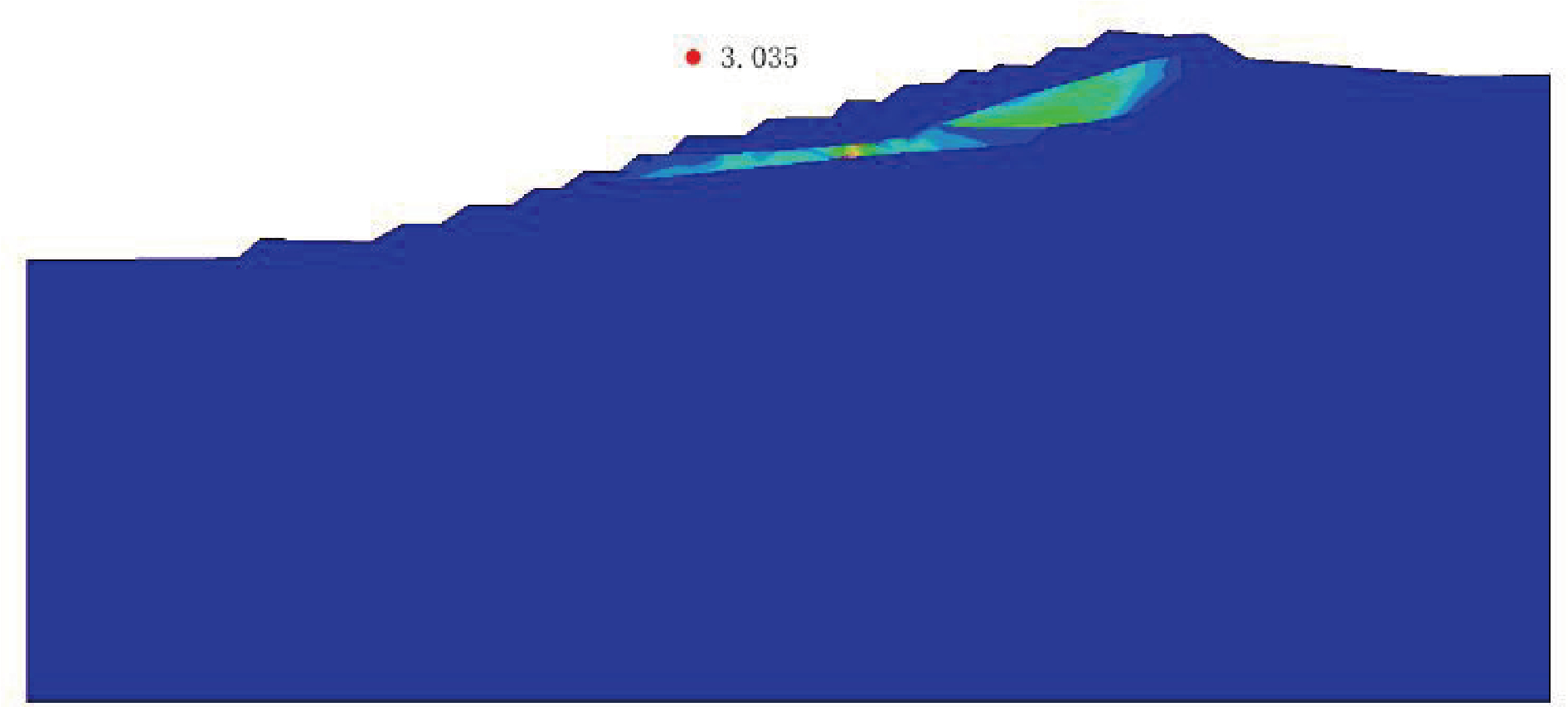
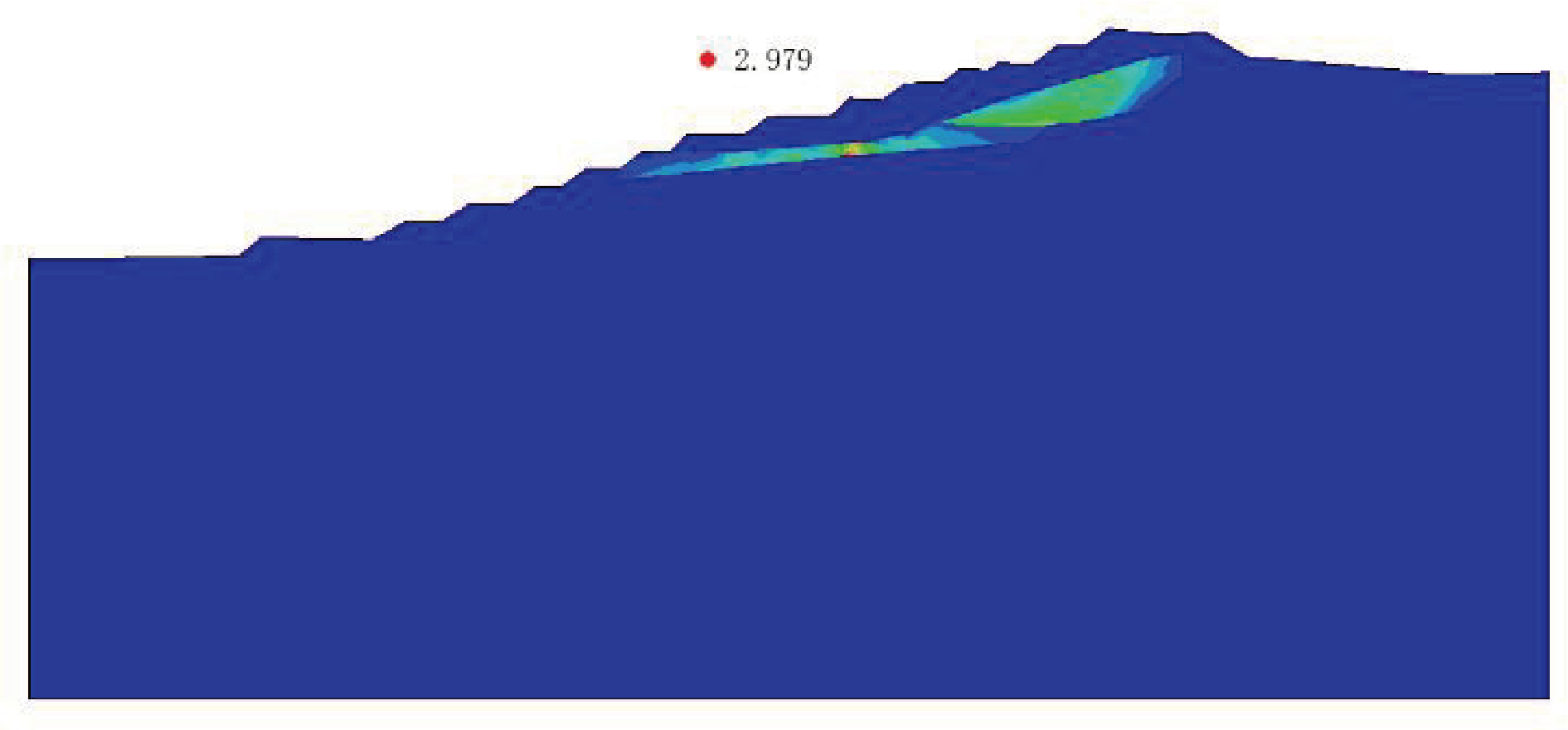
图10 东北区剖面工况Ⅰ计算结果
-
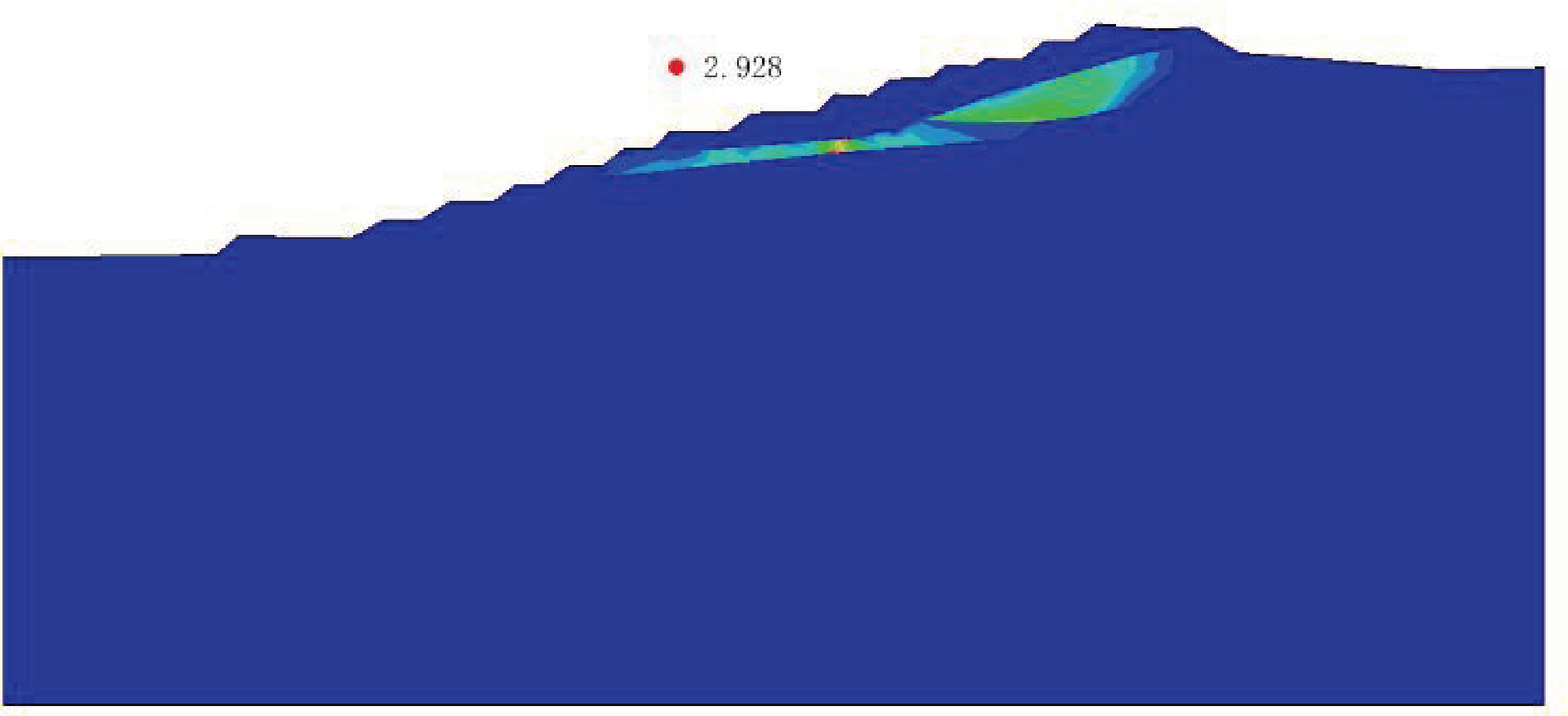
图11 东北区剖面工况Ⅱ计算结果
-
图12 东北区剖面工况Ⅲ计算结果
-
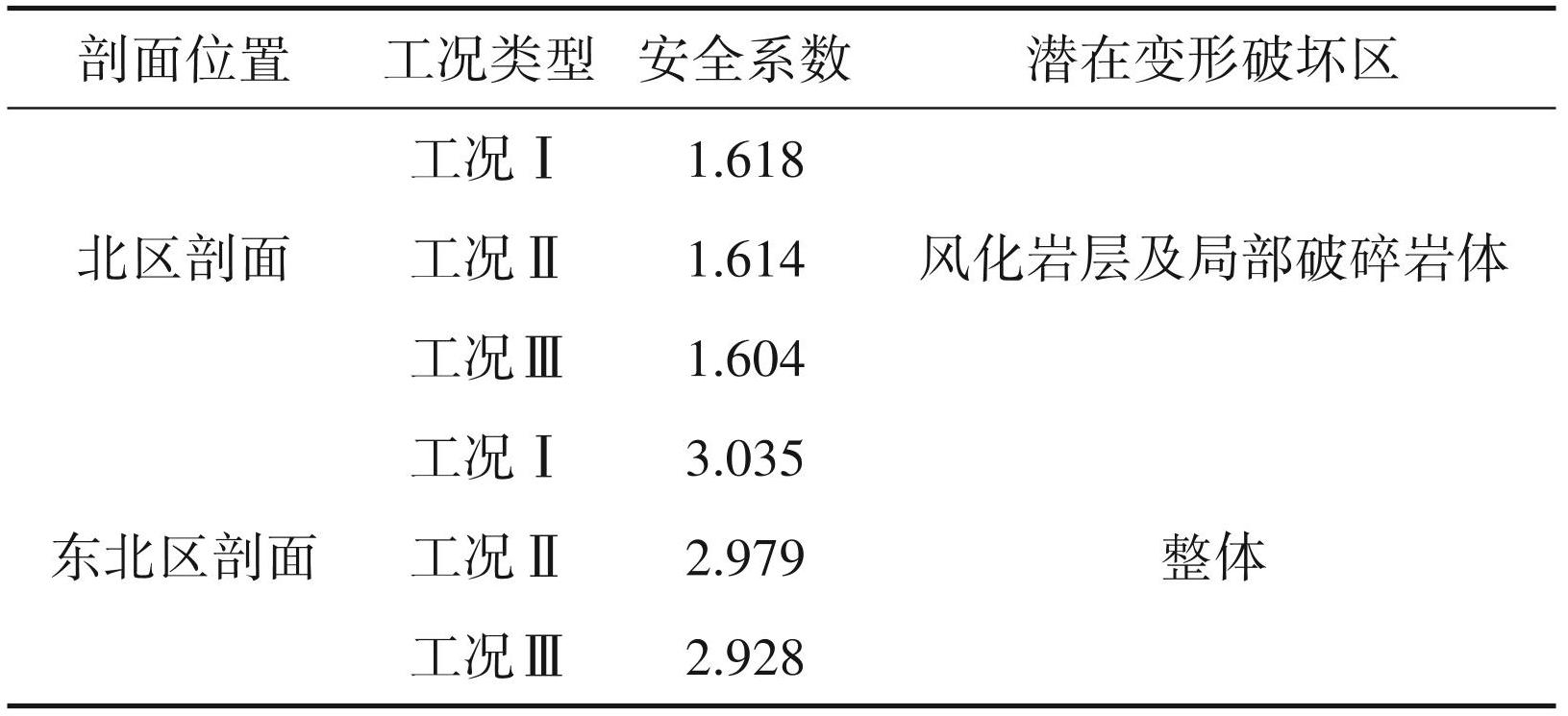
通过计算发现,北区节理岩质边坡剖面处于极限平衡状态,风化岩层的赋存状态及边坡高度对边坡的安全有较大影响,需重点关风化岩层及局部破碎岩体。东北区剖面处整体稳定性相较北区高。
-
数值模拟云图显示,北区的塑性应变区分布如图6、7、8所示,主要集中在顶部风化二长花岗岩层,范围较为集中,使边坡发生局部性破坏。东北区的塑性应变区分布如图10、11、12所示,主要集中在3-2-1碎裂状二长花岗岩层与 3-2-2块状二长花岗岩层,且贯通为连续塑性滑移带,使边坡发生整体性破坏。
-
结合现场实际发现,岩层的风化程度、节理、产状、高度、岩体性质等均影响整体及局部边坡的稳定。在计算中,由于二长花岗岩体参数显著大于碎裂岩,因此考虑岩体的整体边坡稳定性较大,而局部失稳地段被掩盖,进而造成计算安全的边坡,或安全系数很大的边坡,在实际工程中发生跨塌或滑坡。
-
数值模拟结果显示,北区剖面在工况Ⅰ、Ⅱ、Ⅲ 下得出的安全系数模拟结果分别为 1.618、1.614、 1.604,均处于稳定状态。工况Ⅱ转变为工况Ⅲ时,位移区分布位置不变,范围增大。塑性应变区及滑移带范围扩大,但仍集中于中风化二长花岗岩内,边坡滑坡风险增加,破坏形式不发生变化。东北区剖面在工况Ⅰ、Ⅱ、Ⅲ下得出的安全系数模拟结果分别为3. 035、2.979、2.928,均处于稳定状态。3种工况下塑性应变区及滑移带范围不变,均集中于碎裂状二长花岗岩内。
-
3 结论
-
(1)根据工程地质条件、边坡几何形状和边坡面倾向等要素,将采场划分为7个边坡分区,北帮及东北帮受区域动力作用的影响较大,且其倾角偏陡,在开挖扰动过程中容易造成裂隙贯通,发生倾倒、崩塌破坏。
-
(2)北区节理岩质边坡剖面处于极限平衡状态,风化岩层的赋存状态及边坡高度对边坡的安全有较大影响,需重点关注风化岩层及局部破碎岩体。东北区剖面处整体稳定性相较北区高。
-
(3)数值模拟云图显示,北区的塑性应变区主要集中在顶部风化二长花岗岩层,范围较为集中,使边坡发生局部性破坏。东北区的塑性应变区主要集中在3-2-1碎裂状二长花岗岩层与3-2-2块状二长花岗岩层,且贯通为连续塑性滑移带,使边坡发生整体性破坏。
-
参考文献
-
Bai B, Yuan W, Li X C. 2014. A new double reductionMethod for slope stability analysis[J]. Journal of Central South University, 21(3): 1158-1164.
-
Dawson E M, Roth W H, Drescher A. 1999. SlopeStability analysis by strength reduction[J]. Geotechnique, 49(6): 835-840.
-
Deng D P, Li L, Zhao L H. 2016. Limit-equilibrium method for reinforced slope stability and optimum design of antislide micropile parameters[J]. International Journal of Geomechanics: 6016019.
-
Griffiths D V, Lane P A. 1999. Slope stability analysis by finite elements[J]. Geotechnique, 49(3): 387-403.
-
Matsui T, San K C. 1992. Finite element slope stabilityAnalysis by shear strength reduction technique[J]. Soils and Fountions, 32 (1): 59-70.
-
Zienkiewicz O C, Humpheson C, Lewis R W. 1975. Associated and nonassociated visco plasticity and plasticity in soil mechanics[J]. Geotechnique, 25(4): 671-689.
-
陈国庆, 黄润秋, 周辉, 许强, 李天斌. 2013. 边坡渐进破坏的动态强度折减法研究[J]. 岩土力学, 34(4): 1140-1146.
-
付正道. 2014. 基于有限差分强度折减法及其改进折减法的对比研究[D]. 成都: 西南交通大学.
-
郏建磊. 2007. 基于强度折减法的均质土坡稳定性研究[D]. 重庆: 重庆大学.
-
蒋明镜, 江华丽 . 廖优斌 . 2019. 不同形式节理的岩质边坡失稳演化离散元分析[J]. 同济大学学报(自然科学版), 47(2): 167-174.
-
雷远见, 王水林 . 2006. 基于离散元的强度折减法分析岩质边坡稳定性门[J]. 岩土力学, 27(10): 1693-1698.
-
李小春, 袁维, 白冰, 石露 . 2014. 基于局部强度折减法的边坡多滑面分析方法及应用研究[J]. 岩土力学, 35(3): 847-854.
-
欧湘萍, 白楷, 朱云升, 袁灿, 王景, 刘定涛, 刘怀军 . 2009. 基于 FLAC-3D的强度折减法边坡稳定性分析[J]. 武汉理工大学学报, (9): 59-61.
-
孙伟. 2003. 弹塑性有限元法在土坡稳定性分析中的应用[J]. 太原理工大学学报, 34(2): 199-202.
-
唐芬, 郑颖人 . 2009. 强度储备安全系数不同定义对稳定系数的影响[J]. 土木建筑与环境工程, 31(3): 61-65, 97.
-
王广月, 刘健, 王有志. 2005. 岩质边坡平面滑动的模糊可靠度分析 [J]. 岩土力学, 26(S1): 283-286.
-
徐炎兵, 王新志 . 2012. 用强度折减法分析土坡稳定参数敏感性 [J]. 土工基础, 26(4): 44-47.
-
杨光华, 张玉成, 张有祥. 2009. 变模量弹塑性强度折减法及其在边坡稳定分析中的应用[J]. 岩石力学与工程学报, 28(7): 1506- 1512.
-
曾凯波, 周春梅, 吴燕玲, 李先福 . 2009. 基于重度增加法的大冶铁矿边坡稳定性分析[J]. 武汉工程大学学报, 31(12): 32-35.
-
张鲁渝, 郑颖人, 赵尚毅, 时卫民. 2003. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报, 34(1): 21-27.
-
赵尚毅, 郑颖人, 时卫民, 王敬林 . 2002. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报, 24(3): 343-346.
-
郑宏, 李春光, 李焯芬, 葛修润 . 2002. 求解安全系数的有限元法 [J]. 岩土工程学报, 24(5): 626-628.
-
郑颖人, 赵尚毅 . 2004. 有限元强度折减法在土坡与岩坡中的应用 [J]. 岩石力学与工程学报, 23(19): 3381-3388.
-
摘要
边坡稳定性直接关系到露天金属矿山的安全开采,鹿鸣露天矿采区北帮、东北帮边坡节理裂隙发育,一直处于缓慢变形的状态,为分析该采区稳定性,本文根据工程地质条件、边坡几何形状和边坡面倾向等要素,进行了采场边坡分区。采用FLAC 3D软件在研究区域选取2个典型剖面进行了边坡稳定强度折减法分析。结果表明:北区节理岩质边坡剖面处于极限平衡状态,风化岩层的赋存状态及边坡高度对边坡的安全有较大影响,需重点关注风化岩层及局部破碎岩体,塑性应变区主要集中在顶部风化二长花岗岩层,范围较为集中,使边坡发生局部性破坏。东北区剖面处整体稳定性相较北区高,塑性应变区主要集中在碎裂状二长花岗岩层与块状二长花岗岩层,且贯通为连续塑性滑移带,使边坡发生整体性破坏。
Abstract
To analyze the stability of the mining area, the stope slope partition was carried out according to the engineering geological conditions, slope geometry and slope surface inclination. The results show that the jointed rock slope profile in the northern area is in the ultimate equilibrium state, and the occurrence state and slope height of the weathered rock layer have a great impact on the safety of the slope, so it is necessary to pay attention to the weathered rock layer and the local broken rock mass, and the plastic strain zone is mainly concentrated in the top weathered monzogranite layer, which is relatively concentrated, resulting in local failure of the slope. The overall stability of the section in the northeast area is higher than that in the north area, and the plastic strain zone is mainly concentrated in the 3-2-1 fragmented structure monzogranite layer and the 3-2-2 block structure monzogranite layer, and the continuous plastic slip zone is penetrated, resulting in the overall failure of the slope.