-
0 引言
-
边坡稳定性受岩性条件、岩体结构、水文地质条件、边坡形态、地震和爆破等多种因素控制,它们构成一个相互联系、相互影响的整体,其中任何一个因素的改变往往会导致其他因素发生改变,并引起边坡稳定性状态发生改变。尾矿库是指筑坝拦截谷口或围地构成的,用以堆存金属或非金属矿山进行矿石选别后排出尾矿或其他工业废渣的场所。尾矿库是一个具有高势能的人造泥石流危险源,存在溃坝危险,一旦失事,容易造成重特大事故。
-
近些年边坡稳定性方面进行了较多研究。孔圣盛等(2023)以黄山市某尾矿坝为背景,利用Geo-Studio 分析得到坡脚压坡堆石的运用场景;宋宁思等(2023)以四川某尾矿库为工程研究对象,采用 BowTie 模型对浸润线埋深浅事件进行全面定性分析;黄德镛等(2023)在尾矿库稳定性评估中分析研究了尾矿空间变异性和离散型对尾矿库稳定性影响的规律特征;孙世国等(2023)建立尾矿库坝体稳定全局精细化评价体系;刘红岩等(2023)采用 FLAC3D 软件模拟计算了某山谷型尾矿库,并采用流固耦合理论进行了相关研究;陶鹏飞等(2024)引入微动调查方法勘探闭库尾矿库地质结构,开展闭库尾矿库现状稳定性数值模拟分析;刘佳浩等 (2024)以某二等尾矿库为例,采用 Geo-studio 软件分析了尾矿坝在正常水位和洪水位条件下的渗流场和应力场,进而计算得到了不同工况下尾矿坝的坝体稳定性。
-
基于此,本文以甘肃某尾矿库为实际背景,对尾矿库基本资料以及坝体稳定性进行分析,指导企业优化尾矿库的建设和管理,以最大程度地减少对周边区域的不良影响,旨在为相关决策提供科学的依据,确保尾矿库的安全性,从而保障人民生命财产安全。
-
1 静力分析基本理论及计算工况
-
1.1 极限平衡法
-
(1)简化Bishop法
-
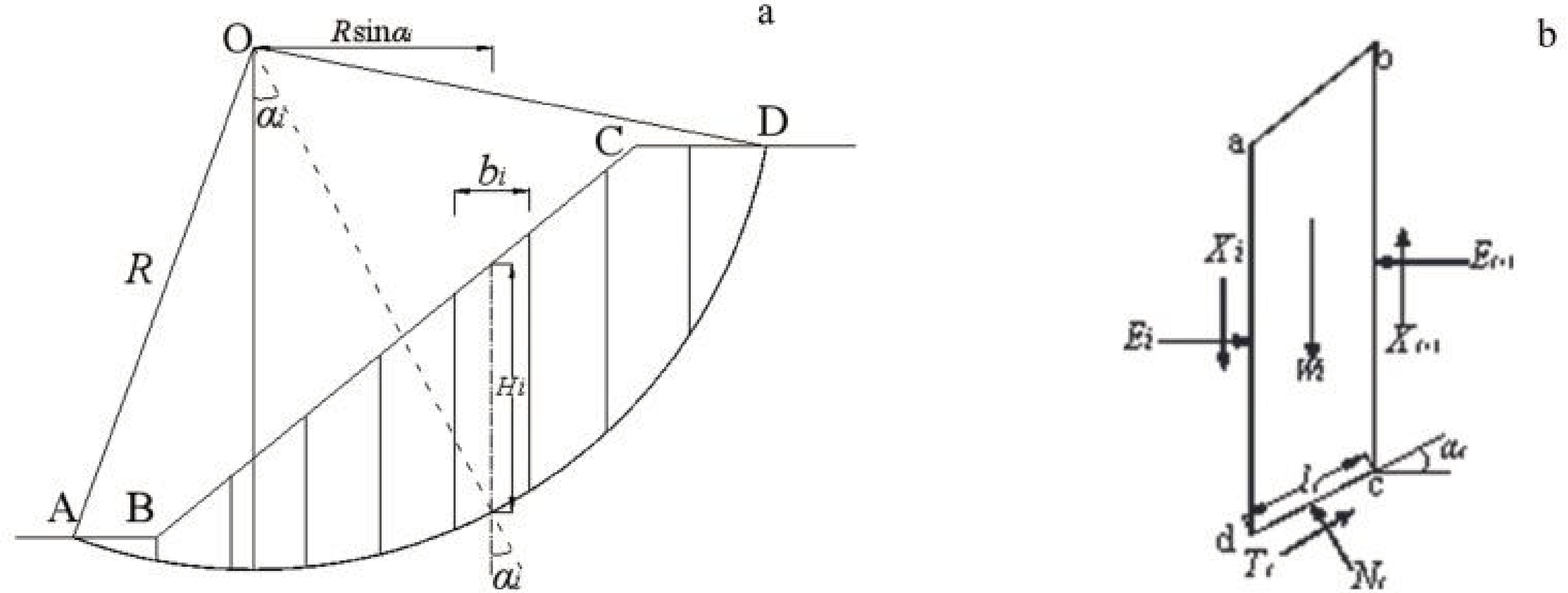
如图1 所示,简化 Bishop 法的基本假设与瑞典条分法差别不大,主要包括以下7点:
-
①边坡问题为平面问题,即可取某一横剖面作为分析对象;②边坡整体为均质材料,其抗剪强度服从摩尔-库伦准则;③条块为刚体,即不考虑滑动土体的变形;④所有条块在滑动面上同时达到极限平衡状态,且滑动面上所有点的安全系数相同; ⑤考虑条块间法向力作用,不考虑切向力,条块受到滑面提供的切向力与法向力合力作用点位于条块底部中心;⑥滑动面为圆弧滑动面;⑦边坡稳定系数定义为滑动面所能提供的最大抗滑力矩与滑体受到的下滑力矩之比,力矩的矩心均为滑动圆弧对应的圆心。
-
分析可得,极限平衡条分模型中共有未知量 6n-2 个,平衡方程及滑面强度方程共 4n 个。简化 Bishop法假定不考虑条块间切向力,仅考虑法向力,同时假定滑面上切向力和法向力的作用点,未知量减少2n-1个。因此,未知量还有6n-2-(2n-1)=4n-1<4n个,超静定问题转变为静定问题。
-
(2)瑞典圆弧法
-
瑞典圆弧法是 Fellennius 于 1927 年提出的,其基本原理如下:
-
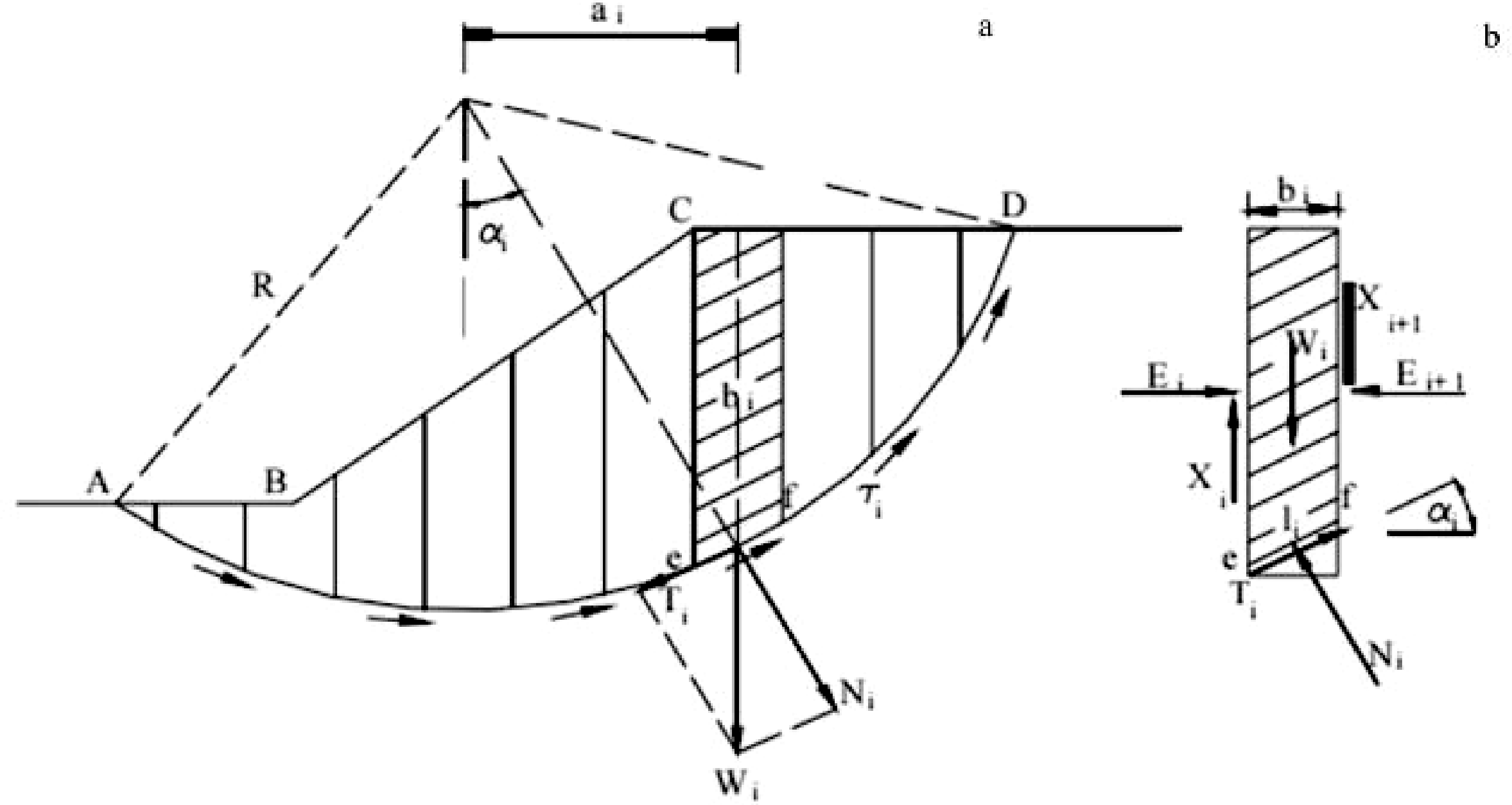
如图2 所示边坡,取单位长度边坡按平面问题计算。设可能滑动面是一圆弧 AD,圆心为 O,半径 R。将滑动体 ABCDA分成许多竖向条块,条块宽度一般可取b=0.1R,任一个条块i上的作用力包括:
-
条块的重力 Wi,其大小、作用点位置及方向均已知。
-
滑动面ef上的法向反力Ni及切向反力Ti,假定 Ni、Ti作用在滑动面ef的中点,它们的大小均未知。
-
图1 简化Bishop法计算示意图
-
a—边坡条分示意图;b—第i个条块受力示意图
-
图2 瑞典圆弧法计算示意图
-
a—边坡条分示意图;b—第i个条块受力示意图
-
条块两侧的法向力 Ei、Ei+1 及竖向剪切力 Xi、 Xi+1,其中 Ei 和 Xi 可由前一个条块的平衡条件求得,而 Ei+1 和 Xi+1 的大小未知,Ei+1 的作用点也未知。
-
由此看到,条块 i 的作用力中有 5 个未知数,但只能建立 3 个平衡条件方程,故为静不定问题。为了求得 Ni、Ti 的值,必须对条块两侧作用力的大小和位置作适当假定。Fellennius 的条分法是不考虑条块两侧的作用力,也即假设 Ei 和 Xi 的合力等于 Ei+1 和 Xi+1 的合力,同时它们的作用线重合,因此条块两侧的作用力互相抵消。这时条块 i仅有作用力 Wi、Ni 及 Ti,根据平衡条件可得整个边坡相应于滑动面AD时的稳定性系数为:
-
1.2 计算工况
-
对尾矿坝正常工况、洪水运行及特殊工况条件下的稳定性进行分析,正常工况考虑尾矿砂堆积至设计高程 1600 m,库水位对应正常水位,正常库水位对应干滩长度为 300 m;洪水运行工况考虑尾矿砂堆积至设计高程 1600 m,防洪标准采用 500 年一遇,此时库水位对应干滩长度为 70 m;特殊工况对应尾矿砂堆积至最终设计标高、正常水位条件下考虑地震影响。
-
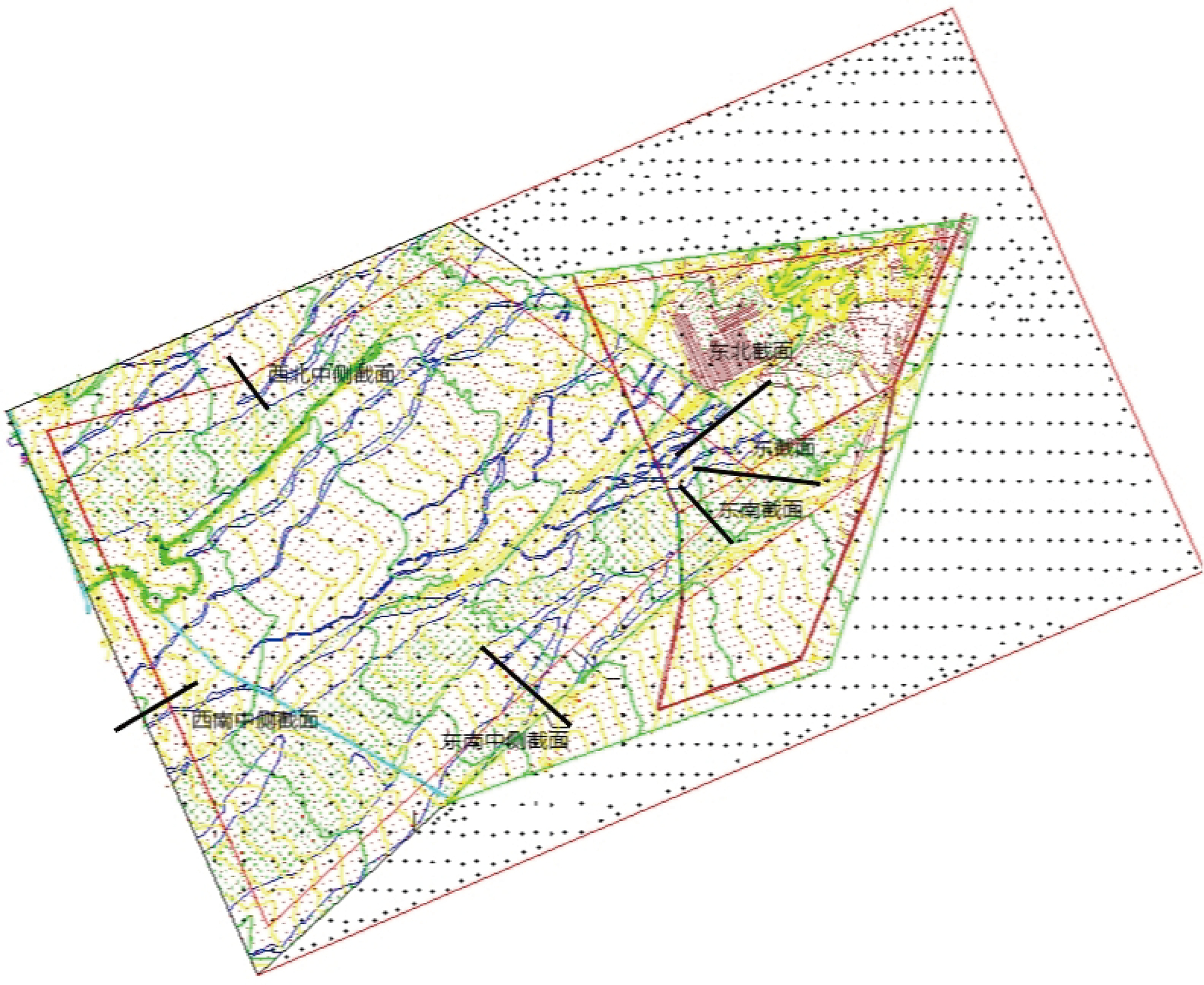
根据《建筑抗震设计规范(2016 年版)》(GB 50011-2010)及《中国地震动参数区划图》(GB 18306-2015),场地抗震设防烈度为 8 度,设计基本地震加速度值为0.20 g,设计地震分组为第二组,场地类别Ⅱ类,特征周期 0.40 s。考虑尾矿堆积面积较广,不同位置处断面形式不同,故计算时分别对不同位置处断面进行计算,断面位置包括东北侧断面、东侧断面、东南侧回填断面、东南中侧断面、西北中侧断面以及西南中侧断面,其中东北侧断面接近最大断面,且东北侧断面、东侧断面计算时考虑相邻采矿区开挖影响。
-
对东北侧和东侧尾矿坝正常工况、洪水运行及特殊工况条件下砂场开采回填和未回填的稳定性进行分析,对东南砂场侧、东南中侧、西北中侧、西南中侧进行正常工况、洪水运行及特殊工况条件下砂场开采回填和未回填的稳定性进行分析,分析截面选取位置示意图如图3所示。
-
图3 截面选取位置示意图
-
东北侧断面、东侧断面、东南侧回填断面、东南中侧断面、西北中侧断面以及西南中侧断面的坝体模型如图4所示。
-
2 参数选取及模型建立
-
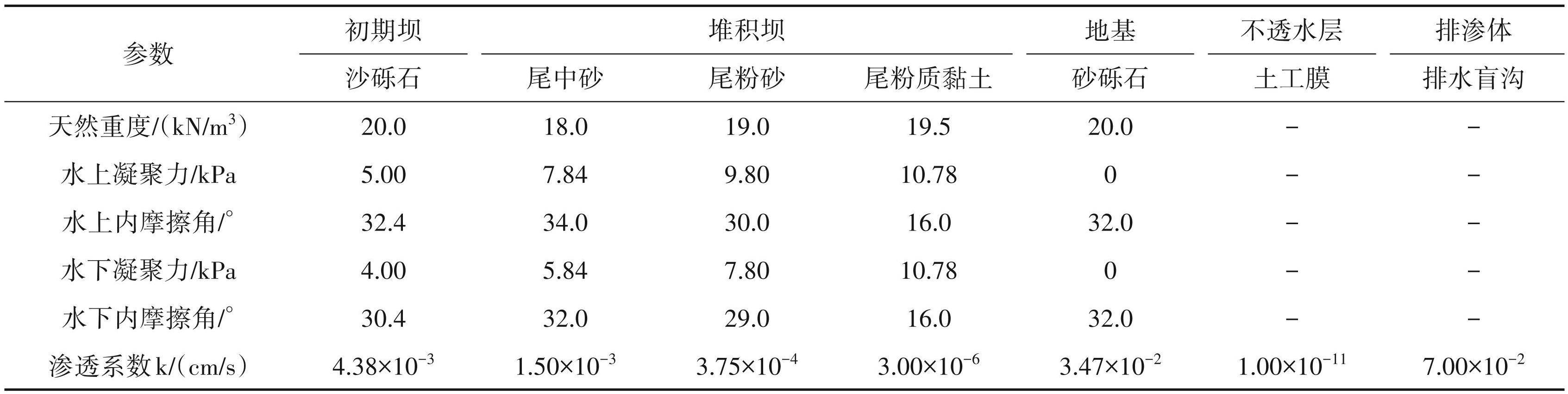
2.1 尾矿坝及下游砂场形态
-
该新建尾矿库库区东南角,将压覆甘肃某建材园采砂场矿权约79998.83 m2,尾矿库下游南采砂场的最大采挖深度为 18.5 m,采用机械采砂,不需爆破作业。为保护尾矿库安全,需设置一定距离的禁采线,禁采线的确定原则为采砂作业形成的采坑不影响尾矿坝的安全稳定。尾矿库东北侧为开采区,设定尾矿库保护范围为50 m,即开采区开挖边界距初期坝坡脚为50 m。
-
图4 尾矿库计算断面图
-
a—东北侧砂场开采至设计深度断面;b—东北开采回填断面;c—东侧砂场开采至设计深度断面;d—东侧砂场开采回填断面;e—东南砂场未开采断面;f—东南中侧断面;g—西北中侧断面;h—西南中侧断面
-
2.2 参数选取
-
坝体的渗流及稳定分析,所使用的计算数据来自《尾矿设施设计规范》(GB 50863-2013)、《某尾矿库稳定性论证分析报告》及其他类似工程,计算所使用的数据见表1。
-
2.3 模型建立
-
尾矿库边坡稳定性分析属于典型的平面应变问题,首先确定模型高度,剖面长度,坡面附加荷载等条件,模拟区域以(0,0)点为起点,在 Y 轴方向上确定模型高度的点,剖面长度在X轴方向上确定,连线建立边坡模型(图5)。按弹塑性模型考虑,采用 Mohr-Coulomb准则。
-
图5 尾矿坝模型
-
3 计算结果及坝体稳定性分析
-
3.1 计算程序
-
采用有限元对尾矿坝稳定渗流进行分析,而后在渗流计算结果的基础上对稳定性进行计算。根据《尾矿安全规程》(GB 39496-2020)规定,尾矿坝稳定性分析采用瑞典圆弧法和简化毕肖普法对典型断面进行极限平衡条分法计算,根据设计资料可知,尾矿库设计最高洪水位对应最小干滩长度为 70 m,正常库水位对应干滩长度为300 m。
-
条分法是建立在摩尔-库仑强度准则、安全系数的定义和静力平衡条件基础上的。若土坡沿某一滑面滑动,则在该滑面上的任一点的土体达到极限平衡状态,即:
-
式(2)中,τf 为抗剪强度(Pa);c' 为有效黏聚力 (Pa);σ'、σ 为滑面上的有效应力和总应力(Pa);ϕ' 为有效摩擦角(°);u为孔隙水压力(Pa)。
-
瑞典法适用于黏性土边坡,计算时假定滑动面为通过坡脚的圆柱面,不考虑土体的内应力分布及各土条之间相互作用力的影响,计算公式为:
-
式(3)中,Fs为最小稳定系数;Ci为第i条块滑面黏聚力(kPa);φi为第 i 条块滑面内摩擦角(°);αi为第 i条块滑面与水平线夹角(°);li为第 i条块滑面长度(m);Wi为第i条块滑面的土体重量(kN);Wqh为水平地震惯性力(kN);Wqv为垂直地震惯性力(kN);Yeq 为圆心至水平地震力作用线的垂直距离(m);Yc为圆心纵坐标(m)。
-
本计算依据《尾矿安全规程》(GB 39496-2020),根据尾矿库运行的工况,其荷载组合见表2,其中荷载类别1系指运行期正常库水位时的稳定渗透压力;荷载类别 2系指坝体自重;荷载类别 3系指坝体及坝基中的孔隙水压力;荷载类别 4 系指设计洪水水位时有可能形成的稳定渗透压力;荷载类别 5系指地震荷载。采用瑞典圆弧法和简化毕肖普法进行稳定性计算,依据《尾矿安全规程》(GB 39496-2020),坝体在各种运行情况下的荷载组合及最小安全系数为:
-
正常工况=坝体自重,当尾矿库为三等库时,瑞典圆弧法最小安全系数为1.2,简化毕肖普法最小安全系数为1.3;洪水运行=最高洪水位+坝体自重,当尾矿库为三等库时,瑞典圆弧法最小安全系数为1.1,简化毕肖普法最小安全系数为1.2;特殊工况=坝体自重+地震,当尾矿库为三等库时,瑞典圆弧法最小安全系数为1. 05,简化毕肖普法最小安全系数为1.15。
-
3.2 边界条件
-
在模型前后施加水平约束,在模型底部施加固定约束。在初期坝上部施加滑动入口,初期坝下部施加滑动出口,滑动面的出口和入口如图6所示。
-
3.3 尾矿坝稳定性分析(瑞典圆弧法)
-
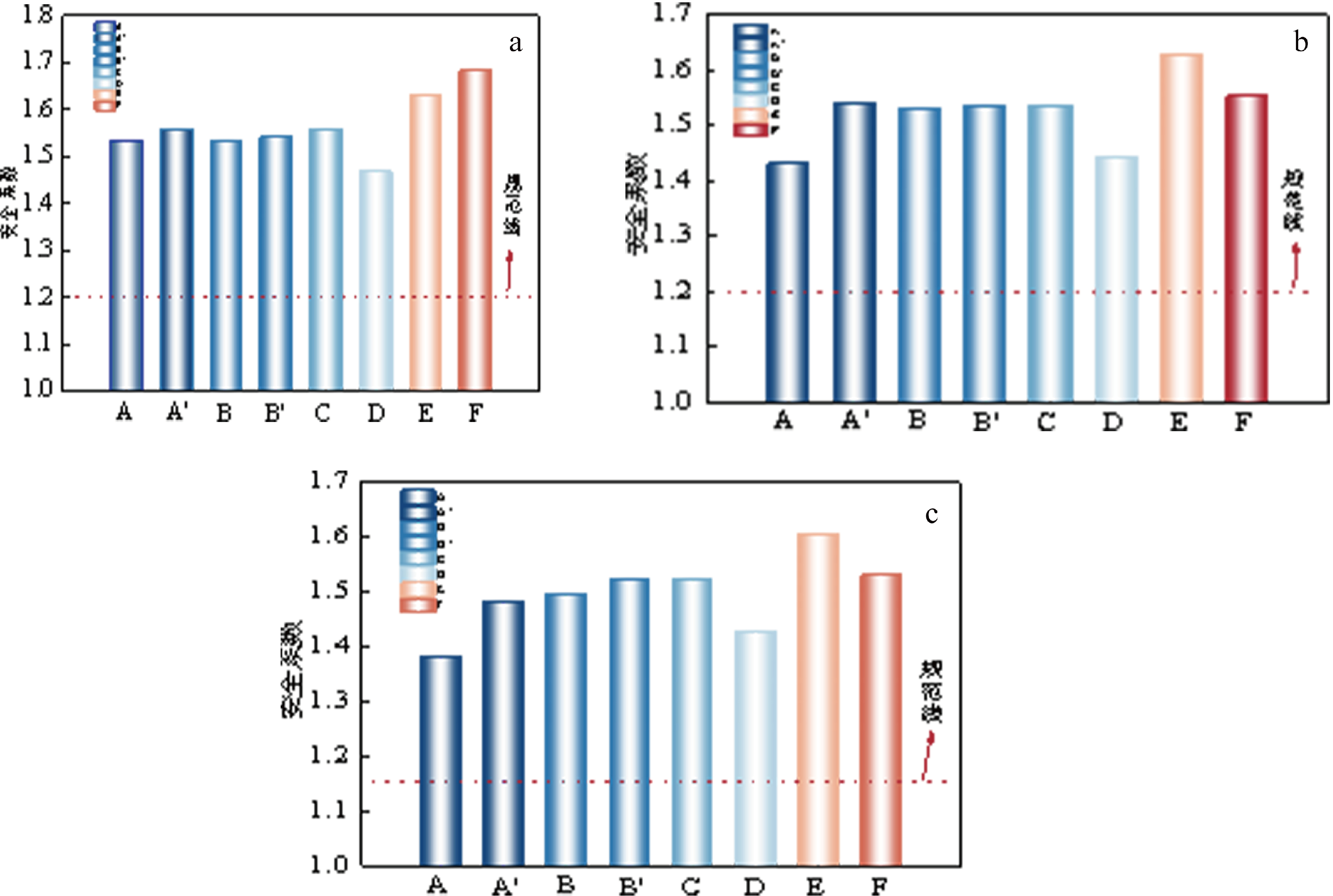
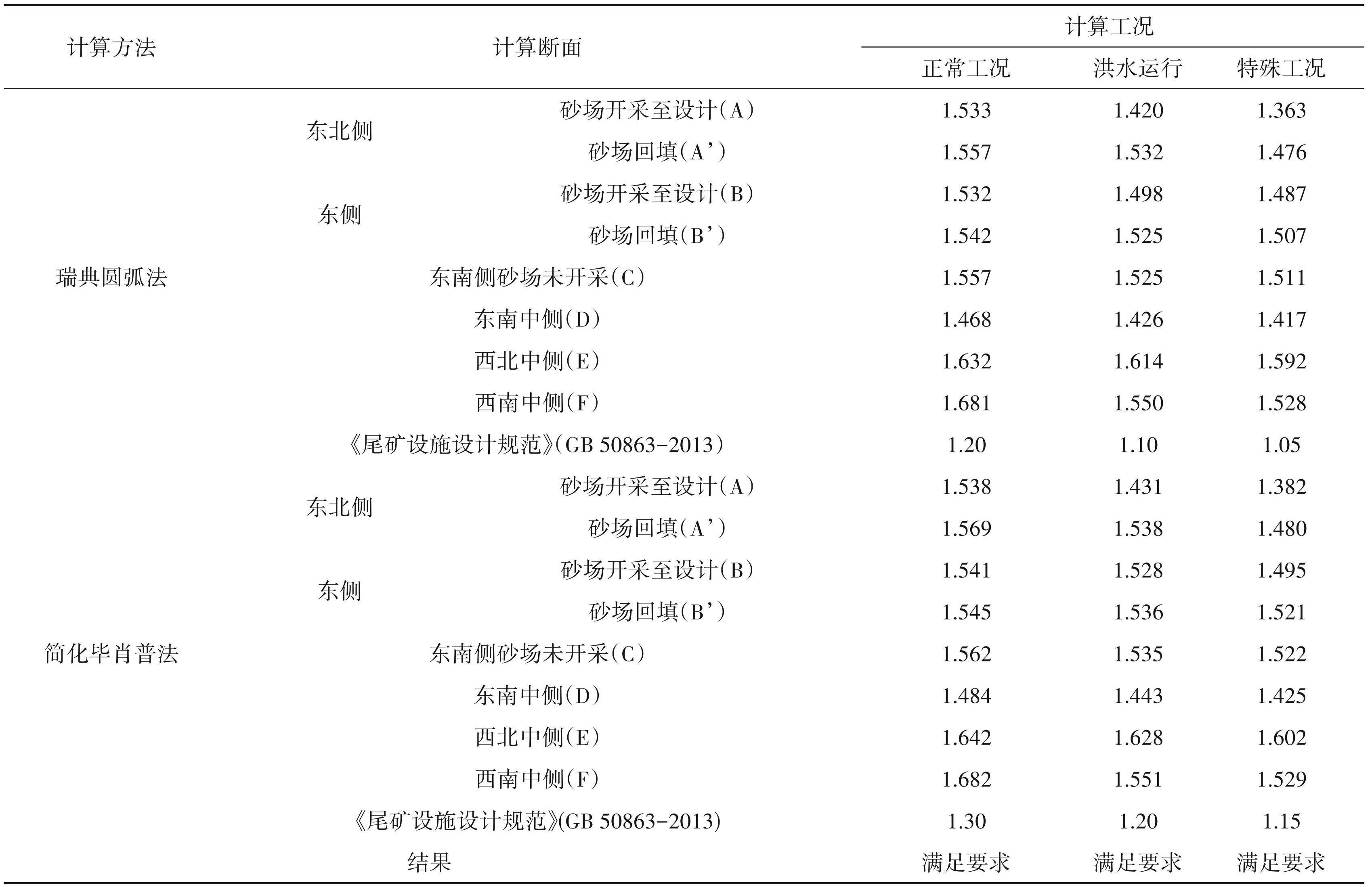
正常工况、洪水工况、特殊工况下尾矿坝堆积至设计高程1600 m时,采用瑞典圆弧法计算所选东北侧断面、东侧断面、东南侧回填断面、东南中侧断面、西北中侧断面以及西南中侧断面 6 个断面的稳定性,得到3种工况下的安全系数(图7)。
-
经瑞典圆弧法稳定性分析,设计坝高正常工况条件下安全系数为1.468~1.681,均大于《尾矿设施设计规范》要求的最小安全系数 1.20;经瑞典圆弧法稳定性分析,设计坝高洪水运行条件下安全系数为1.42~1.614,均大于《尾矿设施设计规范》要求的最小安全系数 1.10;经瑞典圆弧法稳定性分析,设计坝高特殊工况条件下安全系数为 1.363~1.592,均大于《尾矿设施设计规范》要求的最小安全系数 1. 05;砂场对尾矿库的稳定性有一定的影响,未对砂场进行回填的安全系数略低,尾矿库在正常工况、洪水运行及特殊工况下稳定性均满足规范要求。
-
图6 滑动面的出口和入口图
-
图7 瑞典圆弧法安全系数对比图
-
a—正常工况;b—洪水工况;c—特殊工况
-
3.4 尾矿坝稳定性分析(简化毕肖普法)
-
正常工况、洪水工况、特殊工况下尾矿坝堆积至设计高程1600 m时,采用简化毕肖普法计算所选东北侧断面、东侧断面、东南侧回填断面、东南中侧断面、西北中侧断面以及西南中侧断面共 6 个断面的稳定性,得到3种工况下的安全系数(图8)。
-
图8 简化毕肖普法安全系数对比图
-
a—正常工况;b—洪水工况;c—特殊工况
-
经简化毕肖普法稳定性分析,设计坝高正常工况条件下安全系数为1.484~1.682,均大于《尾矿设施设计规范》要求的最小安全系数 1.30;经简化毕肖普法稳定性分析,设计坝高洪水运行条件下安全系数为 1.431~1.628,均大于《尾矿设施设计规范》 要求的最小安全系数1.20;经简化毕肖普法稳定性分析,设计坝高特殊工况条件下安全系数为1.382~1.602,均大于《尾矿设施设计规范》要求的最小安全系数 1.15;砂场对尾矿库的稳定性有一定的影响,未对砂场进行回填的安全系数略低,尾矿库在正常工况、洪水运行及特殊工况工况下稳定性均满足规范要求(表3)。
-
通过计算洪水工况和特殊工况与正常工况之间差值的最大值与最小值,可以得到相比正常工况,洪水工况下计算所得的安全系数降低了 1.1%~8.4%、特殊工况下计算所得的安全系数降低了 2.3%~12%(表3)。
-
在正常、洪水和特殊工况下由瑞典圆弧法所计算的结果,砂场回填后东北侧断面的安全系数分别提升了 1.6%、9.4%、8.3%,东侧断面的安全系数分别提升了 0.7%、2.7%、1.3%;在正常、洪水和特殊工况下由瑞典圆弧法(简化毕肖普法)所计算的结果,砂场回填后东北侧断面的安全系数分别提升了 2. 0%、7.4%、7.1%,东侧断面的安全系数分别提升了0.3%、0.5%、1.7%(表3)。
-
4 结论
-
通过有限元法及极限平衡法对该新建尾矿库静力抗滑稳定性进行分析,得出以下结论:
-
(1)根据数值模拟结果,瑞典圆弧法和简化毕肖普法所计算的尾矿坝所有断面的安全系数均满足规范要求,其中,正常工况下东南中侧断面(D)的安全系数最小。在洪水工况和特殊工况下,位于东北侧的砂场开采至设计深度时计算所得的断面(A) 安全系数最小。
-
(2)根据数值模拟结果,瑞典圆弧法和简化毕肖普法所计算的尾矿坝所有断面的安全系数均满足规范要求整体而言,相较于正常工况,洪水工况下计算所得的安全系数降低了1.1%~8.4%、特殊工况下计算所得的安全系数降低了2.3%~12%。
-
(3)砂场开采至设计深度与砂场回填相比,砂场回填能有效提升尾矿坝的稳定性。在正常、洪水和特殊工况下由瑞典圆弧法(简化毕肖普法)所计算的结果,砂场回填后东北侧断面的安全系数分别提升了 1.6%(2. 0%)、9.4%(7.4%)、8.3%(7.1%),东侧断面的安全系数分别提升了 0.7%(0.3%)、 2.7%(0.5%)、1.3%(1.7%)。
-
参考文献
-
黄德镛, 吕世玮, 高聪, 贾子月, 杜志锦. 2023. 基于空间变异性及沉积规律的尾矿库稳定性模型研究[J]. 矿冶, 32(5): 1‒7, 73.
-
孔圣盛, 何盈, 芮劲草. 2023. 基于Geo-Studio的黄山市某尾矿坝稳定性分析及加固设计[J]. 世界有色金属, (13): 187‒189.
-
刘红岩, 刘康琦, 周月智, 张光雄, 邹宗山, 王光兵 . 2023. 尾矿库渗流场及坝体稳定性的三维数值分析[J]. 矿业研究与开发, 43 (11): 129‒136.
-
刘佳浩, 刘红岩, 邹宗山, 王光兵, 和铁柱, 张光雄 . 2024. 竖向及水平地震作用下尾矿库动力响应及液化稳定性分析[J/OL]. 金属矿山, 1 ‒ 14. http: //kns. cnki. net/kcms/detail/34. 1055. TD. 20231120. 1147. 002. html.
-
宋宁思, 王光进, 何明渝, 刘文连, 孔祥云, 眭素刚, 周汉民, 韩亚兵 . 2023. 地下水位影响尾矿坝稳定性的结构重要度分析[J]. 中国安全生产科学技术, 19(7): 92‒98.
-
孙世国, 臧声涛, 柏朝梅, 薄登 . 2023. 基于全局临界滑移场技术的尾矿库坝体稳定性研究[J]. 黑龙江工业学院学报(综合版), 23 (9): 125‒131.
-
陶鹏飞, 安士凯, 陈永春, 谢毫, 徐燕飞. 2024. 闭库尾矿库现状稳定性分析方法及其应用[J/OL]. 金属矿山, 1‒9. http: //kns. cnki. net/kcms/detail/34. 1055. TD. 20231129. 1829. 006. html.
-
摘要
为确保甘肃某新建尾矿库正常使用时坝体稳定性达标、无溃坝风险,本文利用有限元法及极限平衡法对新建尾矿库进行坝体稳定性分析,用以指导企业优化尾矿库的建设和管理,有效防范坝体失稳溃坝。文中渗流计算通过有限元法结合的方式确定浸润线,稳定计算采用瑞典圆弧法和简化毕肖普法得到尾矿坝在正常工况、洪水工况和特殊工况下6个典型断面的安全系数。结果表明:尾矿坝所有断面的安全系数均满足要求,正常工况下东南中侧断面(D)的安全系数最小,洪水工况和特殊工况下东北侧的砂场开采至设计深度时计算所得的断面(A)安全系数最小;砂场开采至设计深度与砂场回填相比,砂场回填能有效提升尾矿坝的稳定性。
Abstract
In order to ensure that the dam stability of a newly built tailings pond in Gansu province meets the standard and there is no dam break risk during normal use, the finite element method and limit equilibrium method are used to analyze the dam stability of the newly built tailings pond, so as to guide enterprises to optimize the construction and management of the tailings pond and effectively prevent dam instability and dam break. In the seepage calculation, the infiltration line is determined by the finite element method, and the safety factors of six typical sections under normal working conditions, flood working conditions and special working conditions are obtained by the Swedish circular arc method and the simplified Bishop method. The results show that the safety coefficients of all sections of the tailings dam meet the requirements. The safety coefficients of the middle section(D) in the southeast of the tailings dam under normal working conditions are the least, and the safety coefficients of the section (A) calculated when the sand field in the northeast is mined to the design depth under flood conditions and special working conditions are the least. Compared with the backfilling in the sand field, the stability of the tailings dam can be improved effectively.