0 引言

重力勘探已经被广泛地应用于地质构造研究和资源、能源的勘查中，主要研究由地壳上层内物质分布不均匀所引起的重力局部变化（管泽霖和宁津生，1981；曾华霖，2005）。但是在地表观测到的重力值会受多重因素制约，如观测点所在纬度、高程和地形起伏不平等的影响。因此，为获得全部由地壳上层内物质分布不均匀这一单一因素所引起的重力异常，消除其他因素对重力值的影响，就需要对观测重力数据进行校正处理（黄枢谟和何绍渊，1985）。

目前布格重力异常（δ_gB）计算公式如下（中华人民共和国国土资源部，2015）：

式（1）、（2）中：g—测点重力值；δ_gB—布格改正值；γ_o—1980 年大地测量参考系统中的正常重力公式计算大地水准面上的重力值；δ_gT—地形改正值。 φ－重力点地理纬度；h－重力点海拔高程；ρ－中间层密度；a－圆域中间层改正半径。

从式 1、式 2 中可以看出，其缺点是校正中存在正常场校正的高程起算面误差、高程校正误差与地形和中间层校正误差（高庆余，1998）。比如，海拔高程以大地水准面作为校正的基准面，正常重力场是以参考椭球面计算的重力场，由于大地水准面和参考椭球面之间存在高程异常，对于高精度区域重力勘探会引起重力异常的畸变；中间层校正把同一地层分布在大地水准面之上的部分“夷为平地”，但是在地势起伏高原山区，近地表岩性复杂，用统一的校正密度将破坏地层的区域构造格架。如处理不当，将使资料解释结果产生与地质规律不符的现象。

国内外为解决布格重力校正方法中存在的问题，很多学者都开展过研究，如 Ardalan（2004）提出了基于参考椭球面的多重等效圆投影法计算椭球面地形改正的方法；李增涛（2008）推导出一套基于 GRS80 椭球面扇形柱体的地形校正方法。但这些方法主要是针对地形改正和中间层校正提出的，在一定程度上提高了计算精度，并不能从根本上解决目前重力校正存在的问题。王侠和阎汉杰（2008） 提出了一种新的重力校正方法：理论自由空间重力异常处理技术方法，该方法直接将校正值计算到测点所在空间位置，避免了传统布格重力校正方法中存在的误差影响。

因此，本文以河北承德御道口高原地区的实测重力资料为基础，采用理论自由空间重力异常处理技术方法进行了重新处理，通过与布格重力校正方法的资料对比分析，对该方法的对比效果进行了评价，为相关地貌背景下，重力较正的选取提供了借鉴。

1 理论自由空间重力异常处理方法

理论自由空间重力异常是通过推导与大地参考椭球一致的空间任意一点正常场重力公式，直接计算测点位置的正常场重力值，把测点位置的正常场重力值作为校正值，将重力异常直接计算到测点上（式3），而不是按照布格重力异常处理方法，将重力异常计算在水准面或某一基准面上。因此，避免了布格校正所带来的误差。

对于地球表面重力测点，其理论自由空间重力异常按照式3计算：

式（3）中：δg－观测点的理论自由空间重力异常；g－观测点的绝对重力值；γ－观测点正常重力值。

基于这种重力数据处理的思路，骆迪（2013）采用斯托克斯方法直接求解了基于 WGS84 大地坐标系的地球自然表面正常重力公式，得到与WGS84参考椭球一致的重力正常椭球（程鹏飞等，2009），消除了由于大地坐标系参考椭球不一致所引起的纬度误差，且免去了坐标转换和高程转换、校正等过程，消除了由大地水准面与参考椭球面的高程差异带来的“地球物理间接效应”的影响。基于 WGS84 大地坐标系的地球表面正常重力公式如下：

式 （4） 中：$w=\sqrt{\frac{u^2+E^2\frac{\left(1-e^2\right){\mathrm{s}\mathrm{i}\mathrm{n}}^{2}B}{1-e^2{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}B}}{u^2+E^2}}，u=\frac{a{K}^2+H\sqrt{1-e^2{\mathrm{s}\mathrm{i}\mathrm{n}}^{2}B}}{K}，q^{\mathrm{\text{'}}}=\frac{1}{2}\left[-\frac{E}{E^2+u^2}+6\frac{u}{E^2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{E}{u}-\frac{3u^{2}E}{E^2\left(E^2+u^2\right)}-\frac{3}{E}\right]\text{，}q=\frac{1}{2}\left[\left(1+3\frac{u^2}{E^2}\right)\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{E}{u}-3\frac{u}{E}\right]，q_0=\frac{1}{2}\left[\left(1+3\frac{b^2}{E^2}\right)\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{E}{b}-3\frac{b}{E}\right]$

将表1给出参数和推算出的常量代入式4，给出基于WGS84大地坐标系的测点纬度（B）和大地高程 （H），即可得到基于 WGS84椭球的地球自然表面测点的正常重力值。

布格重力校正，高程大多采用大地水准面的海拔高，密度大多采用地表的平均密度或 2.67 g/cm³，选择这些参数往往会引入一定的矫正误差。但在高原山区的区域重力勘探中，采用理论自由空间重力异常处理方法，就可以免去中间层和地形校正，从而避免在高原山区由于密度参数选择不合理和地形校正所引起的误差，从而提高对地质构造探测的精度（励宝恒，1996；孙和平等，2017）。

2 应用效果分析

2.1 研究区地质概况

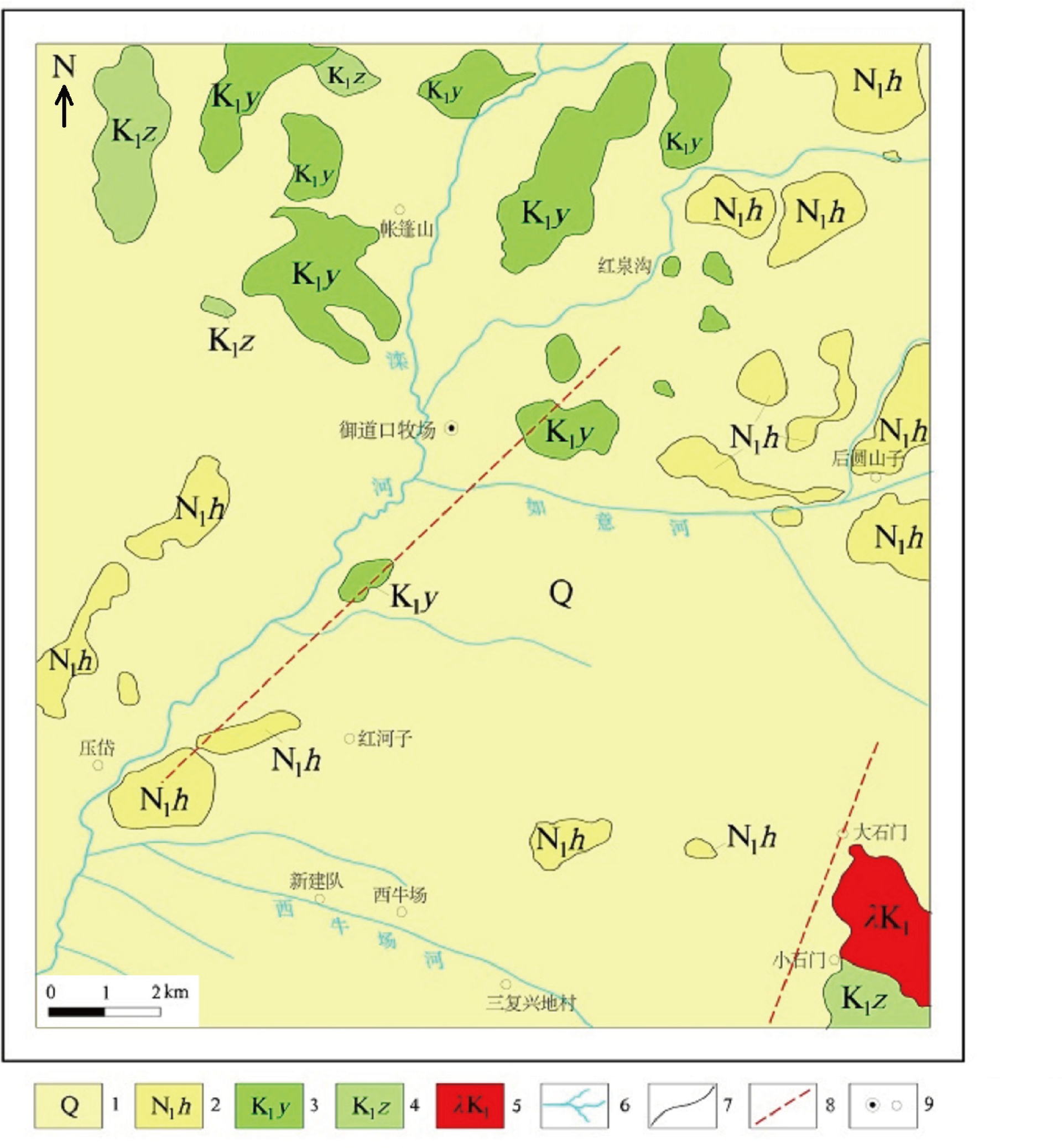
研究区位于河北省承德市围场县御道口牧场，主要位于御道口盆地内，御道口盆地位于温都尔庙 —翁牛特旗加里东地槽褶皱带内（图1），康保—赤峰—开原断裂带以南、尚义—赤城—平泉断裂带以北的内蒙古基底隆起带上，属大兴安岭火山-侵入岩带与燕山火山—侵入岩带的过渡部位（姜山和潘家永，2011）。

御道口盆地内的火山岩系被下白垩统热河群义县组（K₁y）、新近系汉诺坝组（N₁h）不整合覆盖（图2）。盆地内火山岩主要分布于研究区东南部，以早白垩世流纹岩为主。断裂构造主要为蔡家营—御道口断裂带，断裂带总体走向北东 50°，长约 150 km，由 2～3 条硅化角砾岩带及其夹持的挤压破碎带组成，该断裂带对本地区地层、岩浆岩、金属矿化形成和地热资源分布起到控制作用，因此，查明该断裂的空间展布特征对于地质研究和矿产勘查有着重要意义。但因为该断裂带地表行迹不明显，需要采用重力测量等物探方法探测其空间展布特征。

2.2 对比分析

研究区地貌属典型的波状高原，面积为263. 0 km²，海拔高度为1254.81~1554.89 m，平均为1376.85 m，最大高程差300. 08 m，最大重力差值56.91×10^-5 m/s²。

为提高重力测量资料解释准确性，采用理论自由空间重力异常处理技术方法对所测得的重力数据进行了重新处理，通过对比分析布格重力校正方法处理的数据，结合相关地质资料，选取出较为合适的数据处理方法。两种重力数据处理方法的处理结果如下：

1 —一级构造单元界线；2—二级构造单元界线；3—中生代火山喷发中线；4—中新生代沉积盆地界线；5—研究区；Ⅰ—华北板块；Ⅰ₂—内蒙台隆；Ⅰ₄—鄂尔多斯台坳；Ⅰ₅—狼山—白云鄂博台缘坳陷；Ⅰ₆—山西台隆；Ⅰ₇—燕山台褶带；Ⅰ₈—华北断坳；Ⅱ—内蒙古褶皱区：Ⅱ₁—温都尔庙—翁牛特旗加里东地槽褶皱带；Ⅱ₂—西乌珠穆沁旗华力西地槽褶皱带；Ⅱ₃—艾力格庙—锡林浩特中间地块；Ⅱ₄—苏尼特右旗晚华力西地槽褶皱带；Ⅲ—兴安地槽褶皱系：Ⅲ₄—东乌珠穆沁旗中华力西地槽褶皱带

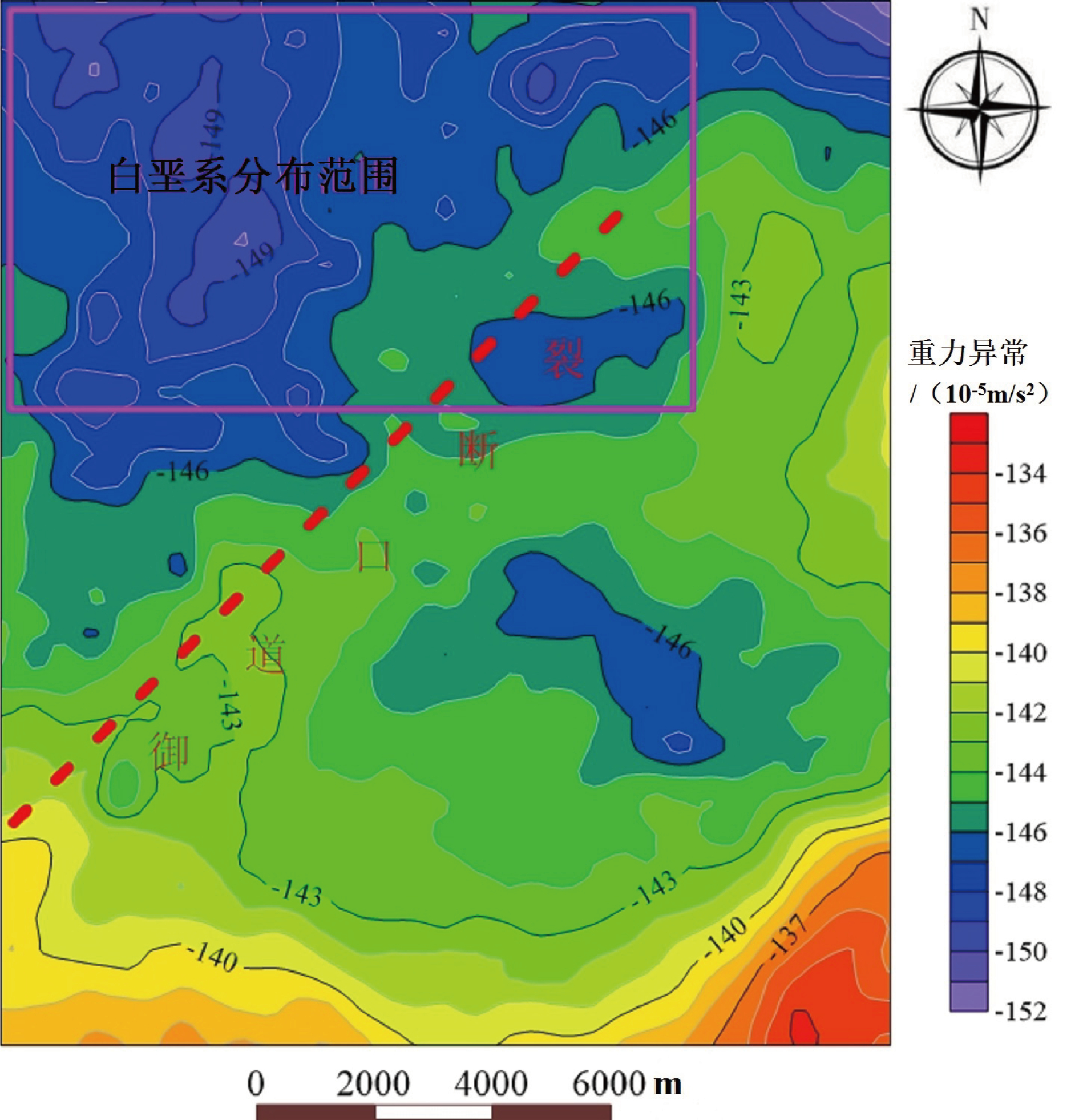
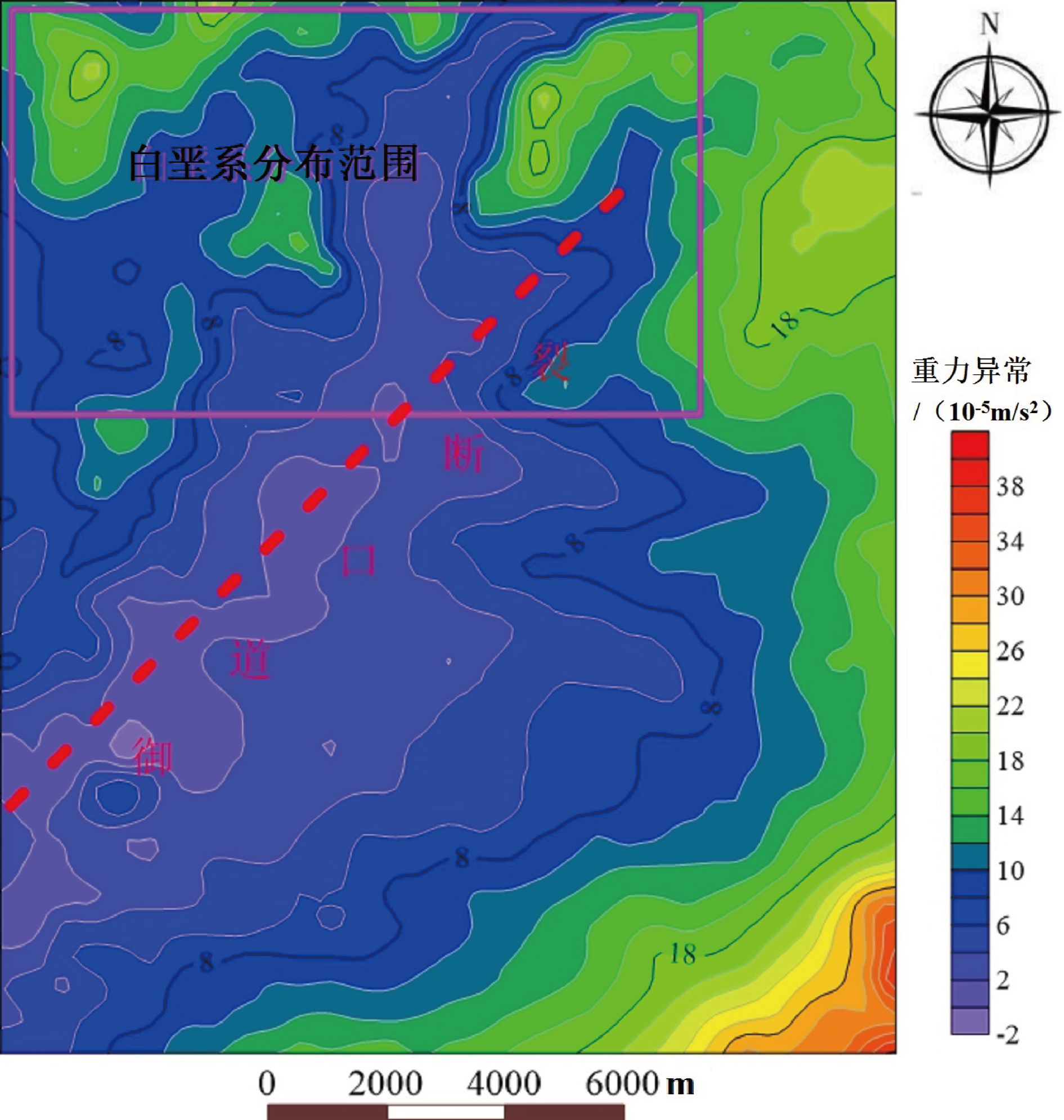
图3为研究区布格重力异常图，主要根据《中国地质调查局地质调查技术标准》（DZ0004—2015）中提出的计算方法（式1）来计算得出布格重力异常数值。图4为理论自由空间重力异常图，采用本文第1 节理论自由空间重力数据处理方法计算（式 1）出的理论自由空间重力异常数值。本文使用数据为实测的 1∶50000 区域重力数据（测网度为 500 m× 500 m），根据数据处理经验（朱自强等，2015；常成和金旺林，2016；张旭和英亚歌，2017；周文月等， 2017；杨渊等，2018；王志宏和李少朋，2019），选取测网度1/2的密度，既采用250 m×250 m网格度网格数据成图。

由于理论自由空间重力异常和布格重力异常数计算方式不同，两种方法所计算出的异常数值大小不同。虽然不同重力异常数值大小存在差异，但研究区内的重力异常相对大小还是有规律可循的，对比图3、图4可以看出，研究区南东部重力异常整体形态较为相似，表现为明显的局部相对高值异常，主要对应于研究区内张家口组凝灰岩和早白垩世潜流纹岩，流纹岩密度较大，且出露于地表，因此该区域表现为局部相对高值异常。而西部则反映为明显的相对低值异常。主要对应于研究区内第四系覆盖区域，由于第四系覆盖层密度较小，因此该区域反映为明显的相对低值异常。同时，对比图2~图4 可以看出，在御道口研究区布格重力异常图 （图3）的南西部存在重力高值异常，自由空间重力异常图上则表现为重力低值异常，与地质图对比可以看出，该区域地表对应为第四系覆盖，说明自由空间重力异常对地层分布情况较为准确。

不同的是在白垩系分布范围，布格重力异常反映明显的重力低值异常，理论自由空间重力异常则反映明显的相对高值异常。一般来说中新生代内陆盆地或地堑等构造单元中，白垩系与其上覆、下伏地层之间普遍存在的一个重要密度界面，其密度差大约为 0.1g/cm³（骆迪等，2013），在沉积岩系较厚的地区，将产生较大的局部异常。从式 1 中可以看出，布格重力异常由于高程和中间层校正误差造成高原山区部分地壳质量的亏损，从而使北部白垩系出露范围反映为相对重力低值异常；而理论自由空间重力处理方法直接将重力异常计算到测点上，避免了布格校正所带来的误差，故表现为相对重力高值异常，反映较为客观，使白垩系局部信息反映更为清晰、丰富。

1 —第四系；2—新近系汉诺坝组玄武岩；3—下白垩统义县组安山岩；4—下白垩统张家口组凝灰岩：5—早白垩世潜流纹岩；6—河流；7—地质界线；8—断裂；9—居民点

在断裂构造上，岩石较为破碎，密度降低，一般表现为重力低值异常。对比图2~图4可以看出，在反映段裂带走向方面，自由空间重力异常（图4）能较好的反映出断裂构造的走向，主要反映明显的线性重力低值异常带，布格重力异常图（图3）在断裂通过处虽然能看到等值线扭曲，但是重力相对低值不连续，不能较好的反应出断裂构造的走向而布格重力异常则反应不明显，主要原因就是中间层校正和高度校正所用的密度值不合理造成的误差。

与研究区区域地质简图（图2）对比也可看出自由空间重力异常（图4）反映断层的重力异常梯级带、扭曲、突变等特征更为强烈，对构造的位置描述也更加准确。

3 结论

（1）理论自由空间重力异常相较于布格重力异常能够较好地反映区域重力场的空间分布形态，清晰地展现更为丰富的局部信息，且在平面上对构造形态表现更加合理、准确，对断层的反映更加清楚。

（2）结合不同的地质目的，合理选择布格校正和理论自由空间重力异常处理方法，可提升资料解释的可靠性。

参考文献