-
0 引言
-
在用平行断面法估算固体矿产资源量中,其对两平行断面间的矿体体积这一估算参数值计算的准确与否,会直接影响到对其估算资源量的成果。多年来虽也有对有关平行断面法计算体积的探讨文章,但均未触及到其存在数理依据不足的实质性问题。在现行的中华人民共和国地质矿产行业标准固体矿产资源量估算规程(DZ/T 0338.2-2020)第 2部分:几何法(以下简称《几何法》)附录“C.4平行断面块段体积(V)”(中华人民共和国自然资源部, 2020)的计算内容中,仍继承了人为的在两平行断面相似下的其用相对面积差的 40% 作指标来择式计算其体积的传统,但其数理依据不足的问题却可导致计算出的是客观性差的体积值参数,从而会影响到其对资源量估算的成果。因此,对该计算体积参数中存在的问题进行商榷探讨、探索其有数理支撑的计算方法是有意义的。
-
1 平行断面法计算其体积的问题探讨
-
1.1 对平行断面法计算其体积的简述
-
对其平行断面法的块段体积计算,现复述《几何法》附录 C(资料性附录)的 C.4 平行断面块段体积(V)的原文(注:复述中对原文内容中的插图未附,有需求者可参见原文,下同)如下:
-
“C.4 平行断面块段体积(V)
-
由于相邻断面矿体形态的差异,分别选用不同的体积计算公式。
-
a)当相邻两断面的矿体形状相似,其相对面积差大于40%时,用截锥形体积公式(见图C.1)。
-
b)当相邻两断面的矿体形状相似,其相对面积差小于或等于40%,用梯形体积公式(见图C.1),也可用截锥形体积公式:
-
c)当矿体为锥形尖灭时,块段体积可用锥形公式计算(见图C.2),也可用截锥形体公式:
-
d)当矿体为楔形尖灭时,块段体积可用楔形公式计算(见图C.2):
-
式(C.4)~式(C.7)中:
-
V—块段的矿体体积(m3);L —两断面之间的距离(m)(楔形公式、锥形公式中,L为外推距离);S1、S2 —块段上矿体在相邻两剖面上对应面积(m2)。”
-
由叶松青和李守义(2011)主编的普通高等教育“十一”五国家级规划教材《矿产勘查学》(2011年第三版)中的第234~235页中,在讲述对平行断面法的块段体积计算的内容中,除包括有其《几何法》附录 C.4对梯形体积、截锥形体积、楔形体积、锥形体积这 4 种体积公式计算的全部核心内容外,还有此附录C.4中所遗漏的对需选择梯形体积与截锥形体积公式计算依据的其“相对面积差”的定义为:(S1-S2)/S1;此外,还讲述有客观计算其平行断面块段体积的似角柱体(辛浦生)公式的计算体积内容,现复述原文(对插图可见原文)如下:
-
“3)当相邻两断面矿体形状不同(图8-11),不论面积相差多少,除有一对应边相等时(长度或厚度),可用梯形体积公式外,其余均应选用似角柱体 (辛浦生)公式,即
-
式中:Sm为似角柱体的平均断面面积(m2);其他符号意义同前。”
-
对上述原文中的此“其他符号意义同前”,现摘录在原文中本公式(8-23)前所讲述的梯形体积与截锥体积公式中的符号意义为:“V—两断面间矿体体积(m3);L—相邻两剖面间距离(m);S1、S2—分别为相邻两断面上矿体面积(m2)。”
-
1.2 对平行断面法计算其体积的问题探讨
-
对前述《几何法》附录 C.4 的其 a)与 b)中的择式计算其体积,就是传统的平行断面法计算体积参数的核心。对此平行断面法的体积计算中存在的问题,数十年来一直有专家学者进行着探讨。马德民(1966)对其选择截锥体、棱柱体、楔形体的体积计算的最大相对误差问题进行了探讨,得出以截锥体为最小达 1.4%、楔形体为最大可达 3%;戴小川 (1992)提出对体积计算公式要停止使用梯形、限制使用截锥体、提倡使用拟柱体(注:为似角柱体)公式,但只是建议要从电子软件与手工仪器两方面着手解决其对中间断面面积难求的问题后推广使用拟柱体公式;李光明(2009)提出停止使用梯形体而均可用截面圆锥体积公式计算其体积;王龙和龙航 (2015)提出取消相对面积差可用截锥体积公式计算体积;贾绍松等(2016)建议限制或停止使用棱柱体和截锥体积公式、提倡统一使用拟柱体体积公式计算矿体块段体积,但文中却是差强人意地均是在两平行断面上其用两工程厚度与其工程间距直线连接成简单的四边形后,进行推导计算其拟柱体体积公式中的中间断面面积参数,因客观上的平行断面更普遍的是为非简单的四边形而无法普遍应用。对《几何法》附录 C.4 的其 a)与 b)两条款的核心内容可归纳为:当相邻两平行断面的矿体形状相似,以其相对面积差≤40% 与>40% 时需分别选择梯形体积公式与截锥形体积公式计算其体积。但依此择式计算体积却在数理依据上存在问题:
-
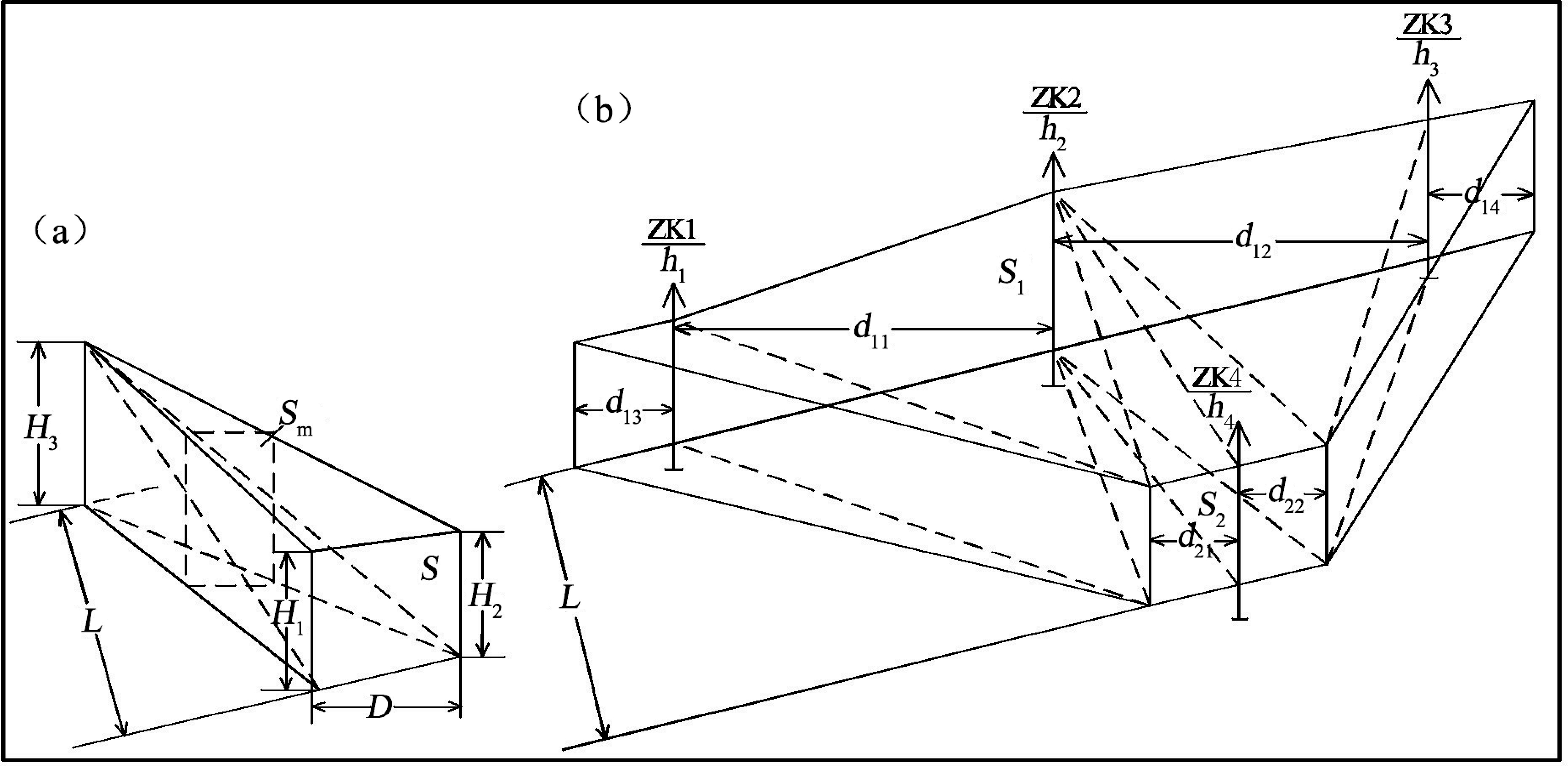
图1 用似楔形体对两平行断面矿体块段的虚拟分割示意图
-
a—客观的似楔形体示意图;b—按图a划分出的各客观单体似楔形体示意图;图a:H1—似楔形体的铅垂棱长(m)及编号;D—矿截面上H1与H2 两棱长间的距离(m);L—两平行剖面间的距离(m);S —左侧图中为在平行剖面上由H1与H2 两铅垂棱长与其D构成的矿截面积(m 2);图b:S1 —平行剖面的矿截面积(m 2)及编号;Sm—平均断面面积(m 2);d11—两铅垂厚度间的水平投影距离(m),下角标数字的第一位为所在剖面的编号、第二位为其线段的编号;ZK1—钻孔编号;h1—矿体铅垂厚度(m)及编号;L—两平行剖面间的距离(m);
-
其一是达到在相邻两平行断面上的矿截形状相似的前提中,如是要达数理上的几何相似,则因在现实中一般就是极少见的存在而极大地限制了其应用,故在择式中对该断面形状相似一般也只能是为非数理的、人为随意认为下的两矿截形状的相似。
-
其二是在前述的相似下,按此两断面的相对面积差的 40% 这一并非是构成区分该两几何形体典型特征的设定来择式计算其体积的数理依据也是似是而非。在数理上,对梯形体一般可描述为是由其与楔形体底端面平行的平行断面所截掉小部分楔形尖灭端后的形体,特征是在两平行断面的矩形图形上的两对应边中有一对应边相等;而对截锥形体一般可描述为是其由与锥体或棱锥体底端面平行的平行断面所截掉部分锥体或棱锥尖灭端后的形体,特征是在其两平行断面图形上的其各对应边边长的比值均相等;故此两特征也就与传统的择式计算体积所依据的两平行断面的相对面积差的 40% 根本没关连。故在对两平行断面上的两矿截在不具上述特征之一时,客观上就应是为在两平行断面间更普遍存在的是不同于梯形体与截锥形体两形体的其似角柱体;故其用前述的选择梯形或截锥形体积公式计算体积就会与此似角柱体的客观体积存在先天性的绝对误差,从而会影响到其对资源量估算的成果。
-
对《几何法》附录 C.4的其 c)与 d),则又分别是对采用锥形与楔形体积公式如何计算其体积的内容,其存在问题为:不应该将不够可采厚度的尖灭端体积部分也计算进入作为估算资源量的体积参数中(不符合GB/T17766-2020中,其对资源量的定义:“经矿产资源勘查查明并经概略研究,预期可经济开采的固体矿产资源,其数量、品位或质量是依据地质信息、地质认识及相关技术要求而估算的”)。若按正确地只对其可采体积计算的话,最终便又归结回到其C.4的a)与b)计算体积的内容上了。
-
对前述《矿产勘查学》所讲述的对平行断面块段体积计算中的其用似角柱体(辛蒲生)公式计算其体积的方法内容中,除需商榷的是对其中的“当两平行断面矿体形状不同……,除有一对应边相等时(长度或厚度),可用梯形体积公式外……”这一在两断面形状不同时是否能有对应边的存在外(笔者认为应该不会存在有对应边的,即便有一其所谓的对应边相等,因其两断面形状的不同故也不会构成其梯形体)?但该公式却是在当相邻两断面矿体形状不同、不论面积相差多少均可客观计算其体积参数的体积计算公式。对此似角柱体(辛浦生)公式,在徐萃薇(1985)编著的《计算方法引论》高校教材中又称为辛普森公式,并综合了对圆锥、圆台、棱锥、棱台、楔形体等体积计算的一个“万能型”计算公式,故只要能正确求解出各形体的其平均断面 (形体的中间平行断面)面积 Sm,便可证明用该公式均可推导回到对客观体积计算的原公式上。不过从该《矿产勘查学》原文中对 Sm需用作图法求解的内容讲述中以及其在原文的插图(图8-11)中的平面直角坐标系方面看,该公式应为更适用于原文中就没明确的是对其在上、下平行断面间的矿体块段体积参数的计算。
-
2 对其计算体积参数新方法的探索
-
为能对在平行剖面中块段矿体体积计算解决前述探讨出的存在问题,以达到对其体积参数值进行客观的计算初衷,笔者初步探索出对两平行剖面间的层状、似层状、透镜状矿体的倾角在<90°时,以在两矿截面上相邻的3个探矿工程见矿的各矿体铅垂厚度作棱长而连接出暂称其为似楔形体的可客观计算其体积的基本体积单元进行计算体积的方法,即本文暂称其为似楔形体积公式法。因该基本体积单元是如图1a 所示的由两可进行客观计算体积的两不同棱锥体所组成,故只要对其平行断面矿体块段适当划分为多个似楔形体基本体积单元计算体积后汇总,则就可达到对其进行客观的体积计算的目的,对此似楔形体体积的计算公式推导如下:
-
在图1a中,是分别由在两平行剖面上的 3个探矿工程见矿的其 H1、H2、H3矿体铅垂厚度作棱长而虚拟连接成其似楔形体这一计算体积的基本单元,在以该似楔形体的尖灭棱长 H3的顶端点与另一剖面上两相邻的 H1、H2棱长的两底端点这三点用直线相连后可成一三角形平面,该平面便可作为其划分出可客观计算似楔形体体积的其下部为三棱锥体与上部为四棱锥体所共用的其棱锥侧面;对此两棱锥体计算的体积汇总则为该似楔形体的体积。因棱锥的体积是为其底面积(S)与垂直于该底面积棱锥体的高(H)乘积的 1/3,故对两棱锥可计算体积如下:
-
对似楔形体其下部的三棱锥体的体积 V1的计算,如将尖灭棱长H3铅垂厚度作此计算三棱锥体积的高(H),则与此高所垂直的底面积就应是此似楔形体中其划分两棱锥体共用的三角形平面的面积经水平投影后形成的三角形面积(St): 即由H1、H2两铅垂厚度棱长间的水平投影距离(D)构成为其水平投影后的三角形平面图形的其底边长,而垂直于该底边长上的三角形的高则为两平行剖面间的距离 (L),故此三棱锥的三角形底面积经水平投影后的面积为:St =L·D/2;故此三棱锥体积(V1)为:
-
而对其上部的四棱锥体的体积(V2)的计算,因其底面积(Sd)为由其同一平行剖面上的 H1、H2两平行的铅垂厚度棱长与其两者间的水平投影距离(D) 所构成四边形面积,即:Sd=D(H1+H2)/2,而垂直于该底面积上的其四棱锥体的高(H)也就是其两平行剖面间的距离(L),故此四棱锥体积(V2)为:
-
通过对其三棱锥体与四棱锥体的体积 V1与 V2 的客观体积的计算结果值汇总,便可得出如下对该似楔形体的体积Vs的客观体积计算公式(1):
-
即
-
式(1)中,Vs为两平行剖面间虚拟划分出的似楔形体的体积(m3 );L为两平行剖面间的距离(m);H1、 H2、H3分别为以3个邻近的探矿工程(或板状外推边界点)见矿的矿体铅垂厚度(m)作其虚拟构成似楔形体的3个棱长,其中H3为楔形尖灭线棱长;D为在同一剖面上H1、H2间的水平投影距离(m)。
-
如用前述的似角柱体(辛浦生)公式对此似楔形体计算其体积,则最终亦可回到体积公式(1)上:
-
因在似楔形体中对应其该似角柱体公式中的两平行断面面积分别为 S1= D(H1+H2)/2、S2=0;而中间平行断面上的平均断面面积 Sm:则为在其楔形体的两各铅垂侧面上的其铅垂厚度的两平行中线边长值(H1+H3)/2、(H2+H3)/2 与此两中线边长间的距离值 D/2 此三者所构成的其四边形图形的面积值,故可得出如下对其Sm计算公式(2):
-
,即为:
-
再将计算 Sm的式(2)代入似角柱体公式中,便可回到前述其对似楔形体计算体积的公式(1)上:
-
因此在有此公式(1)后,对平行剖面中的矿体块段如要客观计算其体积,则可采用如图1b所示的需虚拟划分成按式(1)要求的各似楔形体后,对其计算各体积值后再汇总出其总体积值的方法进行。
-
但要特别注意的是:在虚拟划分其似楔形体时,要在其水平投影平面图上先以两平行剖面上其各矿截的大致中心处工程的矿体铅垂厚度先连出中心基准线后,再从其该线左右两侧合理地连出以其水平投影底面积为最小的各首个似楔形体后,再分别连出其两侧的各似楔形体,然后对其一一计算的各体积值进行汇总。具体过程亦可参照下文对实例的计算过程。
-
3 两方法对实例的计算结果对比
-
3.1 需计算体积参数的实例
-
现对一固体矿产是按400 m×400 m工程间距施工而估算其推断资源量的,如图1b 所示,已知其 S1 与 S2矿截底板的倾角分别为 15°与 10°。两平行剖面(又称断面或矿截面)间的距离(L)为400 m,对板状外推取其1/4的工程间距为100 m。
-
在为S1矿截倾向剖面上,其ZK1、ZK2、ZK3的见矿铅垂厚度分别为:h1=1.2 m、h2=1.5 m、h3=1.3 m,其见矿工程(或板状外推的)间距的水平投影距离则分别为:d11=386.37 m、d12=391.20 m、d13=96.59 m、 d14=96.59 m,则其矿截面积(S1)为:
-
在为(S2)矿截倾向剖面上:其 ZK4 单工程见矿的铅垂厚度为 h4=1.1 m,其沿倾向剖面上对该工程两侧板状外推的水平投影距离分别为:d21=98.48 m、 d22=98.48 m,则其矿截面积(S2)为:S2=98.48×1.1× 2=216.66(m2)。
-
现需计算该平行剖面间估算推断资源量的其块段矿体的体积参数值。
-
3.2 用新方法对实例体积参数的客观计算
-
对该实例的体积计算,首先在其水平投影平面图上需将在分别为两平行剖面矿截上的大致中心处的 ZK2与 ZK4先连接出虚拟中心基准线后,再在此线两侧用就近的见矿工程点分别划出以其似楔形体的水平投影底面积为最小的各首个似楔形体; 其次再依次向外分别划分成如图1b 所示的 6 个似楔形体基本体积单元后,便可用似楔形体公式(1) 计算其所划出的各似楔形体的体积后,再汇总出该总块段体积参数结果值V。
-
在对计算体积的已知参数代入式(1)中的计算过程中,对板状外推边界点棱长值均用了其外推工程中的铅垂厚度棱长值的编号表示,其体积计算结果如下:
-
3.3 按规程中的方法对实例体积参数的计算
-
将已知前述实例中的计算参数:L=400 m、 S1=1310.75 m2、S2=216.66 m2,代入按《几何法》两断面形状相似(在本实例中也只能用人为非数理的相似)、其在相对面积差>40% 时(在实例中已达 83%)需用截锥形体积公式中计算其体积 VZ与为对比中说明择式中的存在问题而试用在其为≤40% 时才用梯形体积公式中计算其体积 VT 的两体积值如下:
-
3.4 两方法对实例计算的结果对比
-
对前述两方法对实例计算的结果,如对用似楔形体公式法计算体积结果用Vs表示,用截锥形体积公式计算体积结果仍用 Vz表示,则其两体积结果值的对比结果可见表1。从表1中可知,其后者的结果值绝对误差为19830.4 m3,其相对误差达7.22%。
-
注:实例中其两平行断面矿截面积的相对面积差(S1-S2)/S1=83%,故需用其截形公式计算其体积。
-
而其试用不该用的梯形体积公式(规程中要求只有在相对面积差≤40% 时才可用此公式计算体积)的其计算值 305482 m3 与似楔形体积结果相比,其试用其梯形体积公式的结果值仅多了 10943 m3,其相对误差为 3.58%。这直观地说明:其传统的择式计算体积的方法是不客观的,该两值可反映出该块段体积应为是属于与梯形体差异相对要偏小的而与截锥形体差异相对要偏大的似角柱体体积。
-
若对其实例中的矿石小体重以 3 t/m3 计,在用按要求的截锥体公式计算的体积参数来估算推断资源量,其估算成果则少5.9491万t,从而说明传统方法的择式计算体积其存在的问题不容忽视。
-
4 结论
-
(1)对传统平行断面法计算其两平行断面块段体积参数中,其存在有先天性的数理不足的问题是:在现实中能达到对两断面的相似是难得的个例,而用其相对面积差确定体积公式计算的其体积参数值的结果也是不太客观的。
-
(2)对探讨出的平行断面块段体积参数计算的新方法,是对其体积参数计算的探索创新;因其有着数理上的支撑优势,也不需其两平行断面矿截形状的相似与考虑其相对面积差的大小,故应更接近对平行断面块段体积参数计算客观世界的认知;因此,应有其一定的理论与积极的现实意义。
-
本文抛砖引玉,不当之处敬请批评指正。
-
致谢 对山西岩玉地质勘测有限公司李东伟高级工程师给予制图的帮助,在此表示感谢!
-
参考文献
-
陈凤忠. 2005. 辛普森公式的统一美[J]. 长春理工大学学报, 3: 59 ‒60, 80.
-
戴小川. 1992. 平行断面法计算矿块体积应注意的问题[J]. 辽宁地质, (3): 285‒287.
-
贾绍松, 孙聪聪, 岳伟佳. 2016. 平行剖面法用棱柱和截锥公式计算块段体积注意的问题[J]. 山东国土资源, 32(2): 72‒75.
-
李光明 . 2009. 关于在平行断面法资源/储量估算中限制使用梯形公式的建议[J]. 山东国土资源, 25(5): 42‒43.
-
刘复元 . 1999. 万能体积公式[J]. 西安工程学院学报, (S1): 99 ‒101.
-
王龙, 龙航 . 2015. 平行断面法计算矿体体积适用公式的探讨[J]. 南方国土资源, (5): 40‒41.
-
徐萃薇. 1985. 计算方法引论[M]. 北京: 高等教育出版社, 92‒95.
-
叶松青, 李守义 . 2011. 矿床勘查学(第三版)[M]. 北京: 地质出版社, 221‒223, 234‒236.
-
中国国家标准化管理委员会 . 2020. 固体矿产资源储量分类(GB/T 1766-2020)[S]. 北京: 中国标准出版社, 1‒5.
-
中华人民共和国自然资源部 . 2020. 固体矿资源量估算规程(DZ/T 0338. 2-2020)第 2部分: 几何法[S]. 北京: 地质出版社, 1‒4, 15
-
摘要
在现行固体矿产资源量估算规程(DZ/T 0338. 2-2020)第 2部分几何法中,其对平行断面块段矿体体积参数的计算采用的是传统的模拟断面形状选择体积计算公式的方法;该方法存在的问题是选择计算体积公式的数理依据不足,从而会影响到其对估算资源量成果的客观性。在文中的实例计算中,采用传统方法的计算结果其相对误差达到了 7. 22%。本研究探讨提出了对平行断面法客观计算矿体体积参数的新方法,可为其估算资源量提供客观的体积参数值成果。
Abstract
In the latest DZ/T 0338. 2-2020 Regulation of Mineral Resources Estimation-Part 2: The Geometric Methods,the parallel section method for estimating solid mineral resources is based on the traditional method of simulating the shape of the ore body to calculate the volume parameters. The problem is that the mathematical basis for the method to choose the calculation volume formula is insufficient, which will affect the objectivity of its estimated resource results. In the example calculation in this paper, the relative error of the calculation results using its traditional method reaches 7. 22%. In this paper, a new method for calculating the volume parameters of ore body by parallel section method is proposed, which can provide objective volume parameter results for its resource estimation.