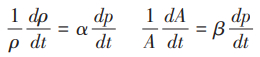引 en

引用本文: 韩加帆，郑双进，魏君陶. 2024. 固井泵关闭过程中的井筒流体流动特性研究［J］. 矿产勘查，15（5）：884-893.

Citation: Han Jiafan，Zheng Shuangjin，Wei Juntao. 2024. Research on the fluid flow characteristics in the process of closing pump in cementing［J］. Mineral Exploration，15（5）：884-893.

固井泵关闭过程中的井筒流体流动特性研究

韩加帆^1,2

机构：

1. 长江大学石油工程学院，湖北武汉 430100
2. 油气钻采工程湖北省重点实验室（长江大学），湖北武汉 430100

×
，郑双进^1,2

机构：

1. 长江大学石油工程学院，湖北武汉 430100
2. 油气钻采工程湖北省重点实验室（长江大学），湖北武汉 430100

×
，魏君陶^1,2

机构：

1. 长江大学石油工程学院，湖北武汉 430100
2. 油气钻采工程湖北省重点实验室（长江大学），湖北武汉 430100

×

1. 长江大学石油工程学院，湖北武汉 430100；
2. 油气钻采工程湖北省重点实验室（长江大学），湖北武汉 430100；

Research on the fluid flow characteristics in the process of closing pump in cementing

HAN Jiafan^1,2

Affiliation：

1. College of Petroleum Engineering， Yangtze University， Wuhan 430100 ， Hubei， China
2. Hubei Key Laboratory of Drilling and Production Engineering for Oil and Gas， Yangtze University， Wuhan 430100 ， Hubei， China

×
，ZHENG Shuangjin^1,2

Affiliation：

1. College of Petroleum Engineering， Yangtze University， Wuhan 430100 ， Hubei， China
2. Hubei Key Laboratory of Drilling and Production Engineering for Oil and Gas， Yangtze University， Wuhan 430100 ， Hubei， China

×
，WEI Juntao^1,2

Affiliation：

1. College of Petroleum Engineering， Yangtze University， Wuhan 430100 ， Hubei， China
2. Hubei Key Laboratory of Drilling and Production Engineering for Oil and Gas， Yangtze University， Wuhan 430100 ， Hubei， China

×

1. College of Petroleum Engineering， Yangtze University， Wuhan 430100 ， Hubei， China；
2. Hubei Key Laboratory of Drilling and Production Engineering for Oil and Gas， Yangtze University， Wuhan 430100 ， Hubei， China；

作者简介:

韩加帆，男，1998年生，硕士生，现从事石油天然气固井工艺研究；E-mail：201601103@yangtzeu.edu.cn。

通讯作者:

郑双进，男，1983年生，博士，教授，现从事石油天然气固井工艺研究；E-mail：Zhengshuangjin@yangtzeu.edu.cn。

中图分类号:TE256

文献标识码:A

文章编号:1674-7801(2024)05-0884-10

DOI:10.20008/j.kckc.202405020

全文
图表
评论
参考文献
相似文献
出版信息

参考文献

Lubinski A， Hsu F H， Nolte K G. 1997. Transient pressure surges due to pipe movement in an oil well［J］. Oil & Gas Science and Technology， 32（3）： 307‒348.

查找原文

参考文献

Mitchell R F. 1988. Dynamic surge/swab pressure predictions［J］. SPE Drilling Engineering， 3（3）： 325‒333.

查找原文

参考文献

陈浩东，杨仲涵，李文拓，徐靖，刘裕，郑双进. 2021. 不同井斜角下的偏心环空固井顶替规律［J］. 矿产勘查， 12（9）： 1953‒1958.

查找原文

参考文献

樊洪海，褚元林. 1995. 起下钻时井眼内动态波动压力的预测［J］. 石油大学学报（自然科学版）， 19（5）： 36‒41.

查找原文

参考文献

郝俊芳. 1992. 平衡钻井与井控［M］. 北京：石油工业出版社， 33‒81.

查找原文

参考文献

金业权，孙泽秋，刘刚. 2013. 控压钻井液动节流压力控制系统仿真分析与试验研究［J］. 石油钻探技术， 41（2）： 109‒113.

查找原文

参考文献

孔祥伟，林元华，邱伊婕. 2014a. 控压钻井中两步关阀阀芯所受瞬变压力研究［J］. 应用力学学报， 31（4）： 20‒24.

查找原文

参考文献

孔祥伟，林元华，邱伊婕. 2014b. 微流量控压钻井中节流阀动作对环空压力的影响［J］. 石油钻探技术， 42（3）： 22‒26.

查找原文

参考文献

孔祥伟，林元华，邱伊婕，郑双进. 2015. 钻井泥浆泵失控/重载引发的波动压力［J］. 石油学报， 36（1）： 114‒119.

查找原文

参考文献

刘刚，蒲家宁. 2003. 瞬变流摩阻计算及摩阻对水力瞬变的影响［J］. 力学与实践， 25（1）： 13‒15.

查找原文

参考文献

刘竹溪，刘光临. 1988. 泵站水锤及其防护［M］. 北京：电力出版社， 63‒79.

查找原文

参考文献

栾鸿儒. 1993. 水泵及水泵站［M］. 北京：中国水利水电出版社.

查找原文

参考文献

栾鸿儒，杨晓东. 1987. 逆止阀旁通管消减停泵水锤的研究和计算［C］//中国机械工程学会流体工程学会泵专业学术讨论会. 陕西：陕西机械学院， 27.

查找原文

参考文献

庞东豪，陈彬，赵维青，赵苏文，严德，郑双进. 2022. 密度差与水泥浆流变参数耦合的水平井固井顶替规律研究［J］. 矿产勘查， 13（2/3）： 302‒308.

查找原文

参考文献

孙秀芳. 2001. 污水泵站水锤计算与缓闭止回阀的应用［J］. 中国给水排水， 17（8）： 48‒49.

查找原文

参考文献

唐晓寅，叶江涛. 2004. 长管水击最大水击压强的解析［J］. 后勤工程学院学报， 20（2）： 32‒36.

查找原文

参考文献

王立辉. 2020. 井筒压力波动条件下钻井液侵入煤岩实验研究［J］. 矿产勘查， 11（2）： 384‒389.

查找原文

参考文献

魏纳，孟英峰，李皋，徐小峰，王在明，杨辉. 2013. 套管阀关阀井下压力动态演变规律的研究［J］. 应用力学学报， 30（3）： 412‒416.

查找原文

参考文献

张迎进，朱忠喜，蔡敏，尚可心. 2008. 钻井泵开启和关闭瞬时水击压力计算［J］. 石油钻探技术， 36（2）： 48‒50.

查找原文

目录contents

摘要 Abstract
关键词 Keywords
0 引言
1 井筒流体流动控制方程
1.1 连续性方程
1.2 运动方程
2 求解方法与边界条件
2.1 求解方法
2.2 边界条件
2.3 多流道计算方法
3 实例计算
3.1 计算基本数据
3.2 关泵过程中井筒流量及压力计算与分析
4 结论
参考文献

摘要

在石油天然气井固井过程中，固井泵关闭过程中由于排量的变化，井筒内的流体流量和压力都会产生一定的波动，势必影响井筒压力安全和环空井壁稳定，因此研究固井泵关闭过程中的井筒流体流动特性十分重要。本文针对该过程中排量瞬时变化导致流体排量和压力波动的问题，将井筒内的流体流动看作一元流体，将管柱看作线弹性体，考虑钻井液与套管的弹性，建立了井筒流体流动控制方程，研究确定了求解方法与边界条件，并开发了相应的计算分析软件。基于实例计算分析了固井泵关闭过程中的井筒流体流动特性。研究结果表明，固井泵瞬时关闭会对井筒压力和环空流量产生不容忽视的波动影响，而随着关泵时间的延长、井深的增大，波动幅度逐渐减小。因此为了保证固井施工安全和防止回流导致水泥浆掺混，优化关泵方式十分重要。本文研究成果也将对于保障固井施工安全和提高固井质量具有一定的指导意义。

Abstract

In the cementing process of narrow density window formation， the fluid flow and pressure in the wellbore will produce certain fluctuations due to the change of displacement during the closure of cementing pump， which will inevitably affect the safety of well pressure and the stability of annular wall. Therefore， it is very important to study the flow characteristics of well fluid during the closure of cementing pump. In this paper， aiming at the problem of fluid displacement and pressure fluctuations caused by the instantaneous change of displacement in this process， the fluid flow in the wellbore is regarded as a univariate fluid， and the pipe string is regarded as a linear elastomer. Only considering the elasticity of drilling fluid and casing， the well fluid flow control equation is established， the solving method and boundary conditions are determined， and the corresponding calculation and analysis software is developed. The flow characteristics of well fluid during the closure of cementing pump are calculated and analyzed based on an example. The results show that the instantaneous closure of cementing pump will produce fluctuations that cannot be ignored on the well pressure and annular flow， and the fluctuation range gradually decreases with the extension of the closure time. Therefore， in order to ensure the safety of cementing construction and prevent the mixing of cement slurry caused by backflow， it is very important to optimize the closure mode of cementing pump. The research results of this paper will also have certain guiding significance for optimizing cementing construction technology and improving cementing quality.

关键词

控制方程；求解方法；边界条件；固井；井筒压力

Keywords

control equation ； solving method ； boundary condition ； well cementing ； wellbore pressure

0 引言
在石油天然气井固井过程中，固井泵关闭过程中由于排量的瞬时变化，井筒内的流体排量和压力都会产生一定的波动（栾鸿儒和杨晓东，1987；刘竹溪和刘光临，1988；栾鸿儒，1993；孙秀芳，2001），势必影响井筒压力安全和环空井壁稳定，所以环空压力剖面的精细计算与控制十分重要。目前国外多侧重于起下钻过程中的波动压力研究，对井筒中由钻柱运动引起的瞬态压力波动现象深入研究，通过揭示规律及建模，提出了相应控制建议（Lal，1983^①； Mitchell，1988；Lubinski et al.，1997）。中国在平衡钻井井筒压力控制技术（郝俊芳，1992），起下钻过程中井眼内的动态压力预测（樊洪海和褚元林， 1995），欠平衡钻井套管阀关阀过程中的井下压力演变规律研究（魏纳等，2013）等方面取得较大进展。但是国内外针对固井工况下的波动压力研究较少，更多的是对影响固井顶替效率的因素进行分析研究（陈浩东等，2021；庞东豪等，2022）。固井时，固井泵关闭过程中，由于排量的变化井筒内的流体流量和压力都会产生一定的波动，如果处理不当，可能导致井筒失稳、流体泄漏等安全问题（王立辉，2020）。因此，开展固井泵关闭过程中的井筒流体流动规律研究具有重要的实际意义。本文基于固井实际工况，建立了固井泵关闭过程中的井筒流体流动控制方程，研究确定了求解方法与边界条件，开发了相应的计算分析软件。结合一口井的实例数据进行了计算，结果表明固井泵瞬时关闭对井筒压力和环空流量都会产生不容忽视的波动影响，随着关泵时间的延长、井深的增大，井底压力和环空流量波动幅度越来越小。为了保证固井施工安全和防止回流导致水泥浆掺混，优化关泵方式十分重要。
1 井筒流体流动控制方程
在建立井筒流体流动控制方程时，为了建模方便，可将井筒内的流体流动看作一元流体，将管柱看作线弹性体，仅考虑钻井液与套管的弹性。
1.1 连续性方程
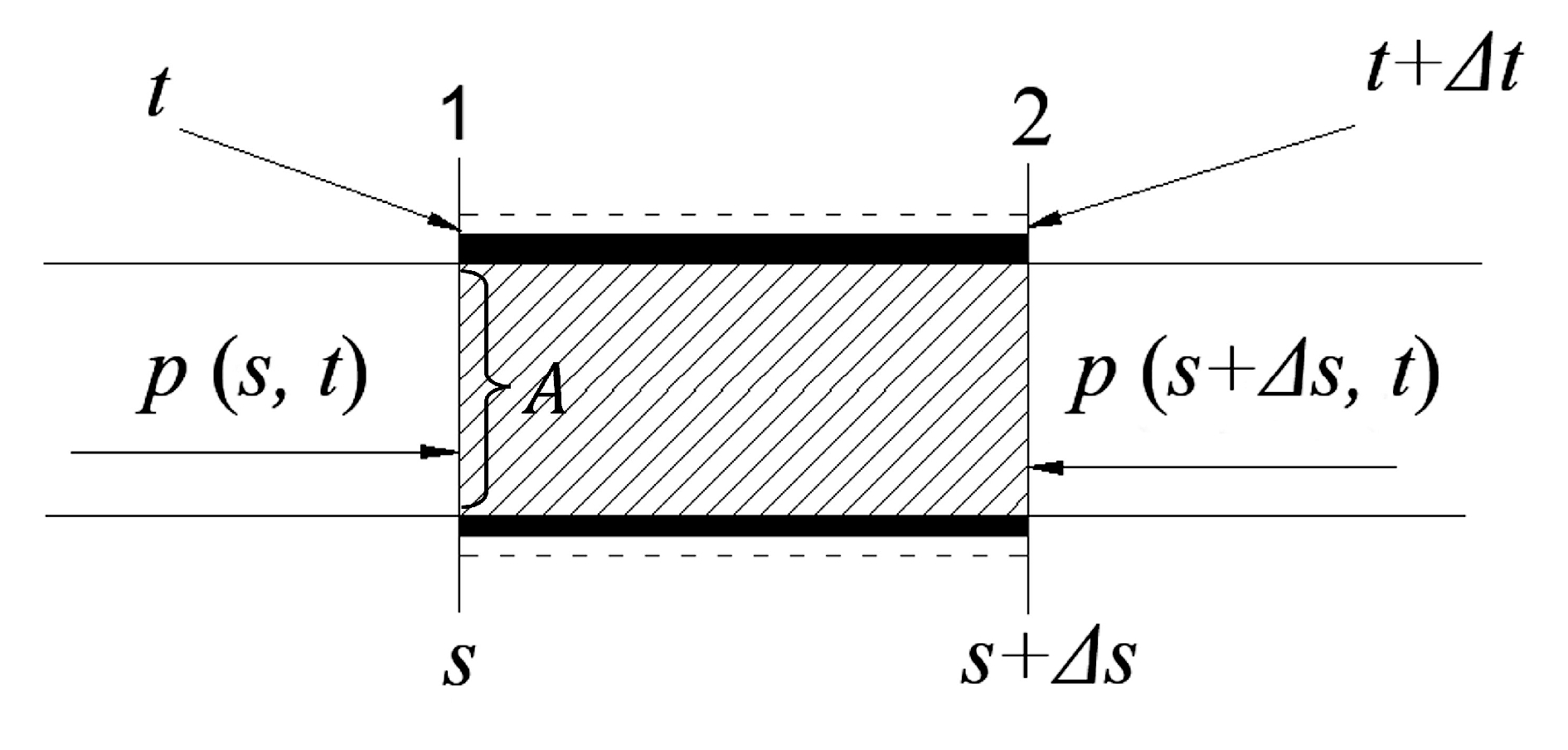
任取固井环空内一微元段（图1）为研究对象，设断面 1 的位置坐标为 s，断面 2 的位置坐标为 s + ∆s，对任意时段∆t内展开分析。
图1 井筒内流道微元示意图
液体从断面 1流入，从断面 2流出，两断面间的距离为∆ s（图1）。设断面1处的面积为A，流速为υ，液体密度为 ρ，过水断面 A 和密度 ρ 都随时间而变化，即：A = A（s，t），ρ = ρ（s，t），在某瞬时取控制体 1-2，根据质量守衡定律可得建立连续性方程：

\frac{1}{ρ} \frac{d ρ}{d t} + \frac{1}{A} \frac{d A}{d t} + \frac{\partial v}{\partial s} = 0

(1)

连续性方程中第一项代表液体密度变化率，即压缩率，由弹性波的压强变化引起；第二项为管道断面变化率，即压缩率，由弹性波的压强变化引起（孔祥伟等，2014a）。
1.2 运动方程
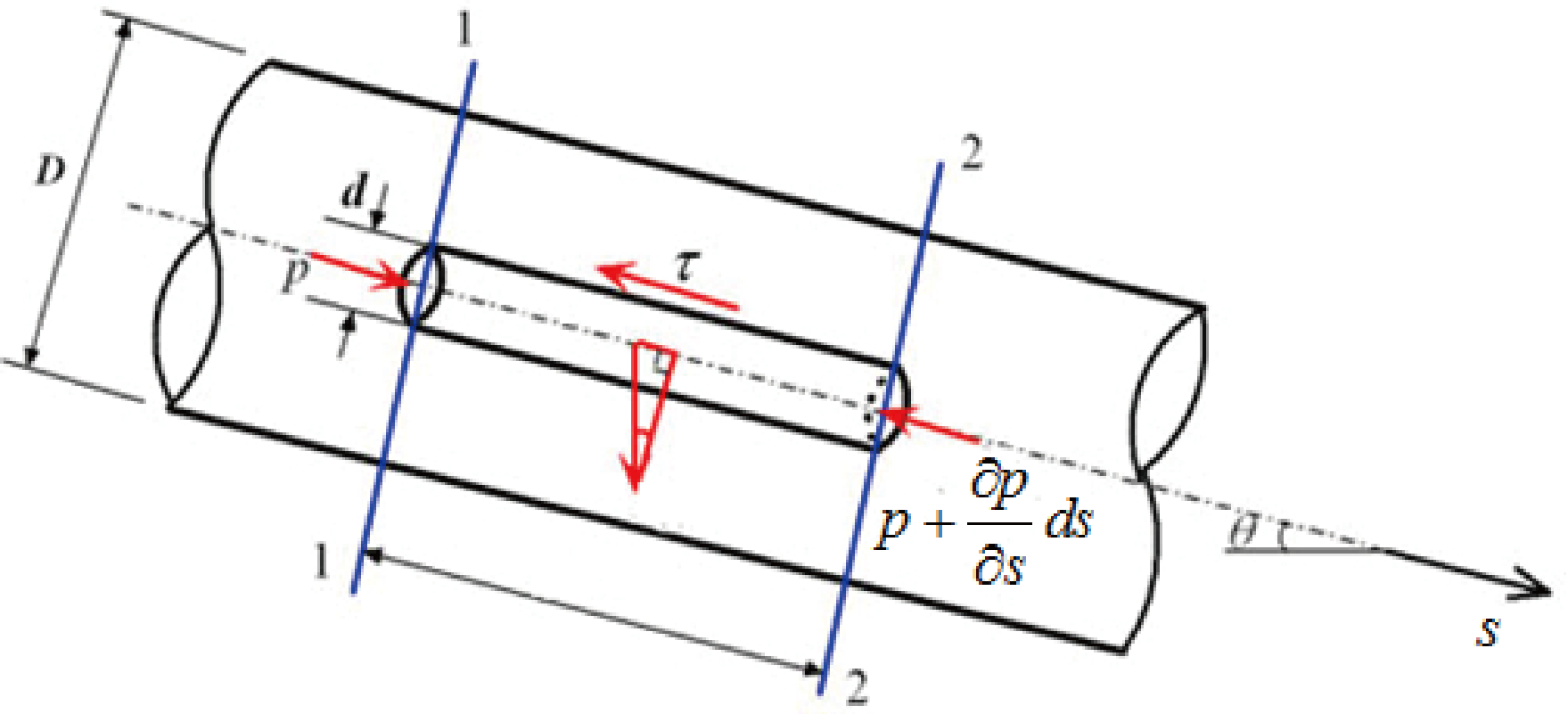
基于固井过程中的实际井眼情况，沿管轴取一微小流体柱（图2），分析作用在其轴向方向的表面力、质量力和加速度力。
图2 流体运动微元示意图
根据牛顿第二定律可得运动方程：

\frac{\partial z}{\partial s} + \frac{1}{γ} \frac{\partial p}{\partial s} + \frac{1}{g} \frac{d v}{d t} + \frac{1}{γ} \frac{τ_{0}}{m} = 0

(2)

式（2）中，z 表示总流断面的平均高程（m）；s 表示流体运动的轴向方向；v表示流体运动速度（m/s）； p 表示总流断面的平均压强（Pa）；τ₀表示管壁切应力（Pa）；m 为水力半径，对圆管，m = D/4；对环空， m =（D₂-D₁）/4，D D₂，D₁ 分别为圆管直径（m），井眼直径（m）、套管外径（m）； $\frac{τ_{0}}{m}$ 表示单位重量液体在单位距离内的压头损失；γ表示重度（N/m³）。
2 求解方法与边界条件
2.1 求解方法
以上两个偏微分方程是具有两个因变量（p，v）和两个自变量（s，t）的拟双曲线型偏微分方程，运用特征线法将其转化为求解常微分形式的特征方程组，然后进行差分求解（孔祥伟等，2014b）。将平均流速 v 转化为流量 Q，同时令 p = γH，p_f = γH_f，则瞬态压力方程的特征式为：

\{\begin{matrix} \frac{Q}{A} \frac{\partial p}{\partial s} + \frac{\partial p}{\partial t} - \frac{ρ g Q}{A} \frac{\partial z}{\partial s} + \frac{ρ C^{2}}{A} \frac{\partial Q}{\partial s} = 0 \\ \frac{\partial p}{\partial s} + \frac{p Q}{A^{2}} \frac{\partial Q}{\partial s} + \frac{ρ}{A} \frac{\partial Q}{\partial t} + p_{f} = 0 \end{matrix}

(3)

以上两个偏微分方程是具有两个因变量（ p，Q）和两个自变量（s，t）的拟双曲线型偏微分方程，对这两个方程进行任意常数的线性组合可得：

\begin{matrix} \frac{\partial p}{\partial s} + \frac{p Q}{A^{2}} \frac{\partial Q}{\partial s} + \frac{ρ}{A} \frac{\partial Q}{\partial t} + p_{f} + \\ k (\frac{Q}{A} \frac{\partial p}{\partial s} + \frac{\partial p}{\partial t} - \frac{ρ g Q}{A} \frac{\partial z}{\partial s} + \frac{ρ C^{2}}{A} \frac{\partial Q}{\partial s}) = 0 \end{matrix}

(4)

式（3~4）中，Q 为流速（m/s）；p为压力（Pa）；C为压力波传播速度（m/s）；s 为井筒轴线坐标（m）；g 为重力加速度（m/s²）；t为时间（s）。
进行如下整理：

\begin{matrix} k [(\frac{1}{k} + \frac{Q}{A}) \frac{\partial p}{\partial s} + \frac{\partial p}{\partial t}] + \frac{ρ}{A} [(\frac{Q}{A} + k C^{2}) \frac{\partial Q}{\partial s} + \frac{\partial Q}{\partial t}] + \\ p_{f} - k \frac{ρ g Q}{A} \frac{\partial z}{\partial s} = 0 \end{matrix}

(5)

令 $\frac{d s}{d t} = (\frac{1}{k} + \frac{Q}{A}) = (\frac{Q}{A} + k C^{2})$ ，解得 $k = \pm \frac{1}{C}$ ，上式可化为如下特征方程组：

C^{+} \{\begin{matrix} d p + \frac{ρ C}{A} d Q + C (p_{f} - \frac{ρ g ν}{C} \frac{\partial τ}{\partial s}) d t = 0 \\ \frac{d s}{d t} = ν + C \end{matrix}

(6)

C^{-} \{\begin{matrix} - d p + \frac{ρ C}{A} d Q + C (p_{f} - \frac{ρ g v}{C} \frac{\partial z}{\partial s}) d t = 0 \\ \frac{d s}{d t} = v - C \end{matrix}

(8)

上述两对常微分方程组统称为特征方程组，该方程组的解就是井筒流体流动控制方程所描述波动问题的解（张迎进等，2008；孔祥伟等，2015）。
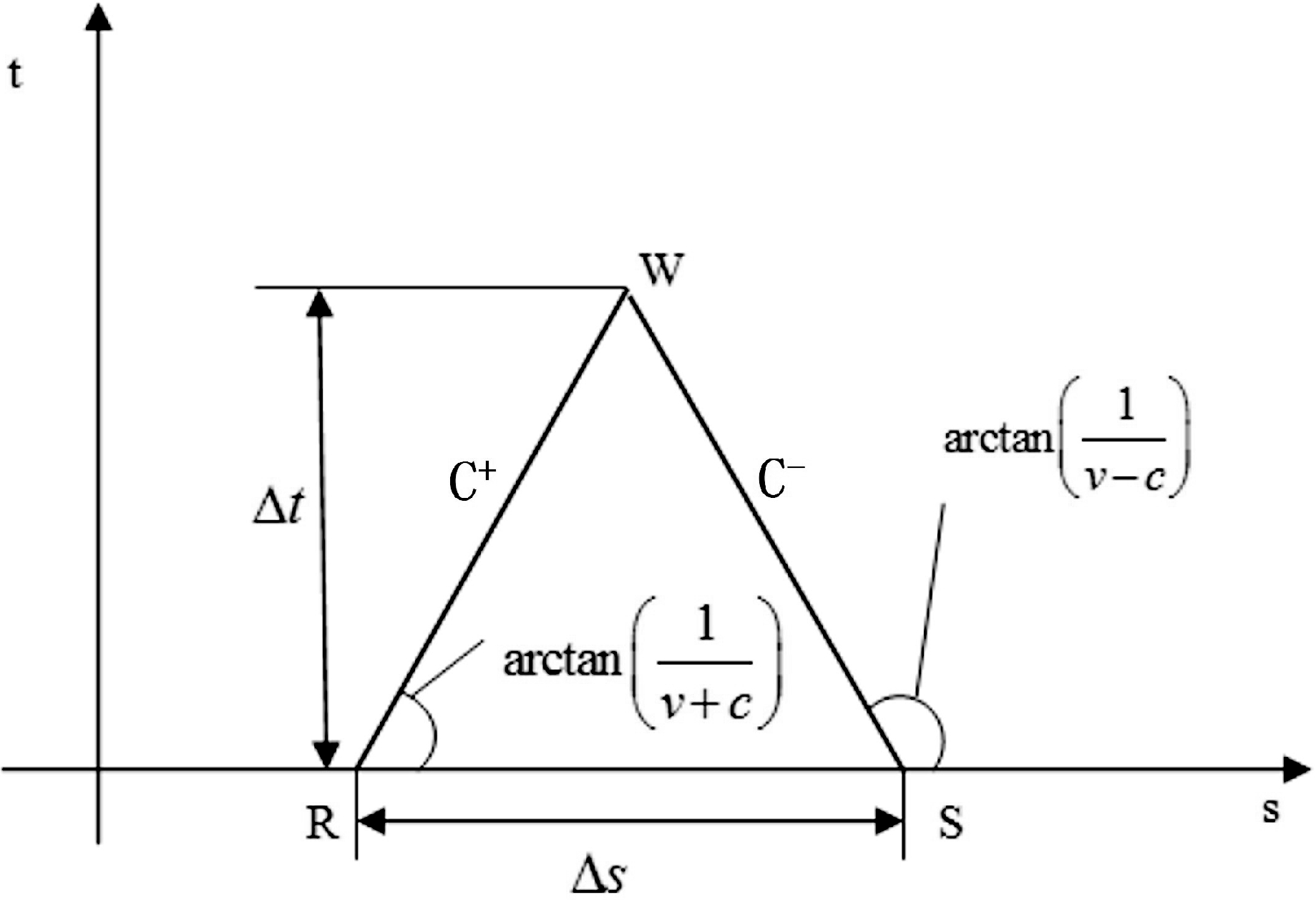
图3 特征线图
上述两对常微分方程组统称为特征方程组，图3 中的 C⁺ 即为顺波特征线，C^-即为逆波特征线。将常微分方程（6）和（8）分别沿 C⁺ 和 C^-两条特征曲线进行求解，即可求出各点的压力和流量（刘刚和蒲家宁，2003；唐晓寅和叶江涛，2004）。将方程式（6）中的各项沿图3中的顺行波特征线C⁺ 积分可得：

\int_{P_{R}}^{P_{Ψ}} d p + \int_{Q_{E}}^{Q_{W}} \frac{ρ C}{A} d Q + \int_{t_{R}}^{t_{W}} C (p_{f} - \frac{ρ g v}{C} \frac{\partial z}{\partial s}) d t = 0

(10)

将方程式（8）中的各项沿图3 中的逆行波特征线C^-积分可得：

- \int_{P_{S}}^{P_{Ψ}} d p + \int_{Q_{s}}^{Q_{Ψ}} \frac{ρ C}{A} d Q + \int_{t_{s}}^{t_{W}} C (p_{f} + \frac{ρ g v}{C} \frac{\partial z}{\partial s}) d t = 0

(11)

由于上面两式中最后两项的被积函数 $C (p_{f} + \frac{ρ g v}{C} \frac{\partial z}{\partial s})$ 与 $C (p_{f} - \frac{ρ g v}{C} \frac{\partial z}{\partial s})$ 随时间 t 或位置 s 的变化规律未知，导致积分十分困难。为了计算简便并保证一定的精度，采用一阶近似处理方法，即用已知R 点或S点的流速v_R、v_s取代上面两个式子中被积函数中的流速，积分后的结果为：

p_{W} - p_{R} + \frac{ρ C}{A} (Q_{W} - Q_{R}) + C p_{f R} Δ t = 0

(12)

- p_{W} + p_{s} + \frac{ρ C}{A} (Q_{W} - Q_{S}) + C p_{f S} Δ t = 0

(13)

其中：
$p_{f R} = (p_{f} - \frac{ρ g v}{C} \frac{\partial z}{\partial s}), p_{f s} = (p_{f} + \frac{ρ g v}{C} \frac{\partial z}{\partial s})$
在求解过程中，由于管路不同的截面 A 对应不同的压力波传播速度 c，数值计算过程中要求时间步长 Δt和空间步长 Δs必须满足下式才能使得计算稳定并且具有一定的精度：

Δ t ⩽ \frac{Δ s_{i}}{{|c_{i} + v_{i}|}_{m a x}}

(14)

通过上式即可计算出全管网上差分网格所能允许取的最大时间步长。
2.2 边界条件
（1）环空流道和管柱内流道的井口边界点
由于在瞬态压力计算时是以大气压为基准的，因此环空井口边界上压力为零，流量由前向特征线方程求得。由于套管口的流量已知，故流量由后特征线方程求得，其边界条件为：

\{\begin{matrix} P_{W} = 0 \\ Q_{W} = \frac{P_{R} + \frac{ρ C_{R} Q_{R}}{A_{R}} - C_{R} Δ t P_{f R}}{\frac{ρ C_{R}}{A_{R}}} \end{matrix}

(15)

\{\begin{matrix} P_{W} = P_{S} + \frac{ρ_{S} C_{S}}{A_{S}} (Q_{W} - Q_{S}) + C_{S} Δ t P_{f S} \\ Q_{W} = 已 知 \end{matrix}

(16)

（2）井底流道的井底边界点
不考虑水泥浆在井底的渗透，井底流道的井底边界上流量为零，压力由前向特征线方程求得，其边界条件为：

\{\begin{matrix} Q_{W} = 0 \\ P_{W} = P_{R} + \frac{ρ C_{R}}{A_{R}} Q_{R} - C_{R} Δ t P_{f R} \end{matrix}

(17)

2.3 多流道计算方法
前述介绍的是等直径单流道情况下瞬态压力和流量的计算方法。对于固井实际条件下的多流道情况，在运用上述方法之前，需要就一些问题进行专门处理。在多流道条件下，由于各流道的直径及材质不一定相同，故压力波的传播速度不一定相同，本文就如何选择Δt和Δs及连接点和汇交点的问题进行了针对性研究。
（1）Δt和Δs的选择
为了便于进行多流道计算，应选择相同的 Δs 值，然后由下式计算Δt：

Δ t = \frac{Δ s}{\bar{C}} \times 0.95

(18)

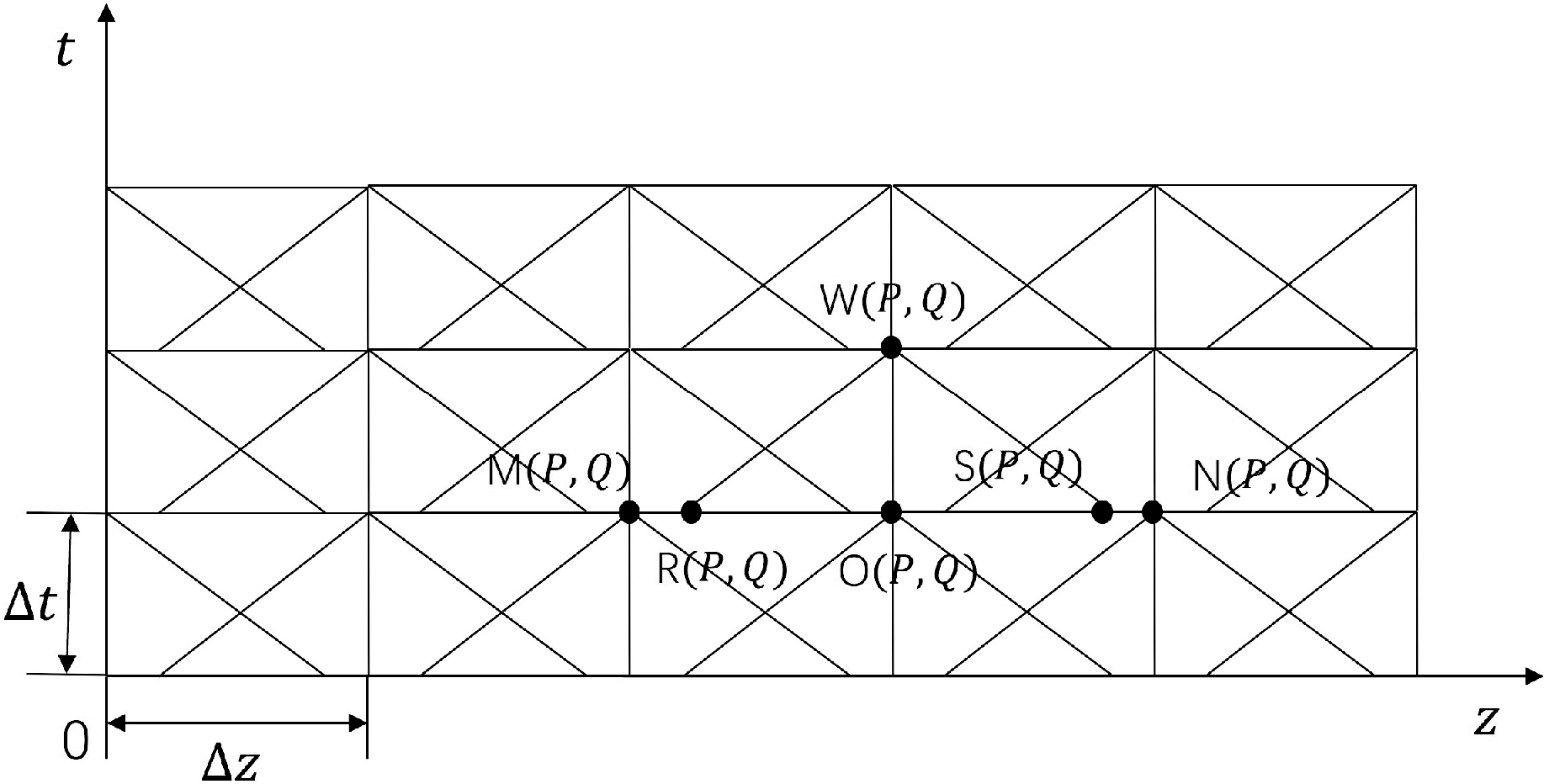
式（18）中， $\bar{C}$ 是各流道中任意处的最大压力波传播速度，系数 0.95 为经验值，是为了保证满足稳定性准则而设置的。不过这样构造的 z-t 网格图， WM不能近似代表前向特征线WR，WN也不能近似代表后向特征线 WS（图4），故在求解时还需进行插值。
图4 方网格加插值方法示意图
（2）插值方法
如图4 所示，若已经获得了第一条时间基线上所有点的 P、Q 值，即 M、O、N 点的 P、Q 值为已知，要求 W 点的 P、Q 值。通过 W 点画两条斜率各为 dz/dt = v₀ + C₀和dz/dt = v₀-C₀的直线，这样的两条线经过 R 和 S，则瞬态压力方程沿 WR 和 WS 是成立的，且满足它们的两条特征线方程。
可以这样认为，以使这两个斜率值接近 dz/dt = v_R + C_R 和 dz/dt = v_S-C_S 或接 dz/dt = v_W + C_W 和 dz/dt = v_W-C_W 为好，但在这一阶段内，由于变量 v_R、v_S、C_R、C_S、v_W和C_W 均未知，需要运用内插法在 M 和O之间求得v_R和C_R，在O和N之间求得v_S和C_S，以上即说明了进行插值的理由。
如果Δx是一个很小的值，则可以采用节点加密的分段线性插值法。首先必须计算 RO 和 OS 的值（图4）：

\{\begin{matrix} R O = (v_{0} + C_{0}) Δ t \\ O S = (v_{0} - V_{0}) Δ t \end{matrix}

(19)

这里需要检查 RO 和 OS两者是否都小于 Δs，否则需要检查参与计算的数据是否合理，如给定的 Δt 值是否过大等。
求出 RO 和 OS 后，即可用节点加密的分段线性插值求得R点和S点的P值和Q值：

\{\begin{matrix} Q_{R} = Q_{o} - (Q_{o} - Q_{M}) \frac{R O}{Δ s} \\ P_{R} = P_{o} - (P_{o} - P_{M}) \frac{R O}{Δ s} \end{matrix}

(20)

\{\begin{matrix} Q_{S} = Q_{o} - (Q_{o} - Q_{N}) \frac{O S}{Δ s} \\ P_{S} = P_{o} - (P_{o} - P_{N}) \frac{O S}{Δ s} \end{matrix}

(21)

求出 R 点和 S 点的内插值后，即可利用特征线方程求解 W 点的 P值和 Q 值。最初计算 R点和 S点的位置时以 v₀、C₀ 值为基础，所以计算出 W 点的值后可以利用平均值为基础的斜率来重新进行计算，即以 $\frac{d z}{d t} = (\frac{v_{R} + v_{W}}{2} + \frac{C_{R} + C_{W}}{2})$ 重新确定 R 的位置，以 $\frac{d z}{d t} = (\frac{v_{S} + v_{W}}{2} - \frac{C_{S} + C_{W}}{2})$ 重新确定S的位置，即：

\{\begin{matrix} R O = (\frac{v_{R} + v_{W}}{2} + \frac{C_{R} + C_{W}}{2}) Δ t \\ O S = (\frac{C_{S} + C_{W}}{2} + \frac{v_{S} + v_{W}}{2}) Δ t \end{matrix}

(22)

利用式（20~21）重新计算 Q_R（v_R）、C_R、Q_S（v_S）、 C_S，全部过程要重复到 Q_W、C_W 各自的两个相邻值差别很小为止。
（3）汇交点的处理
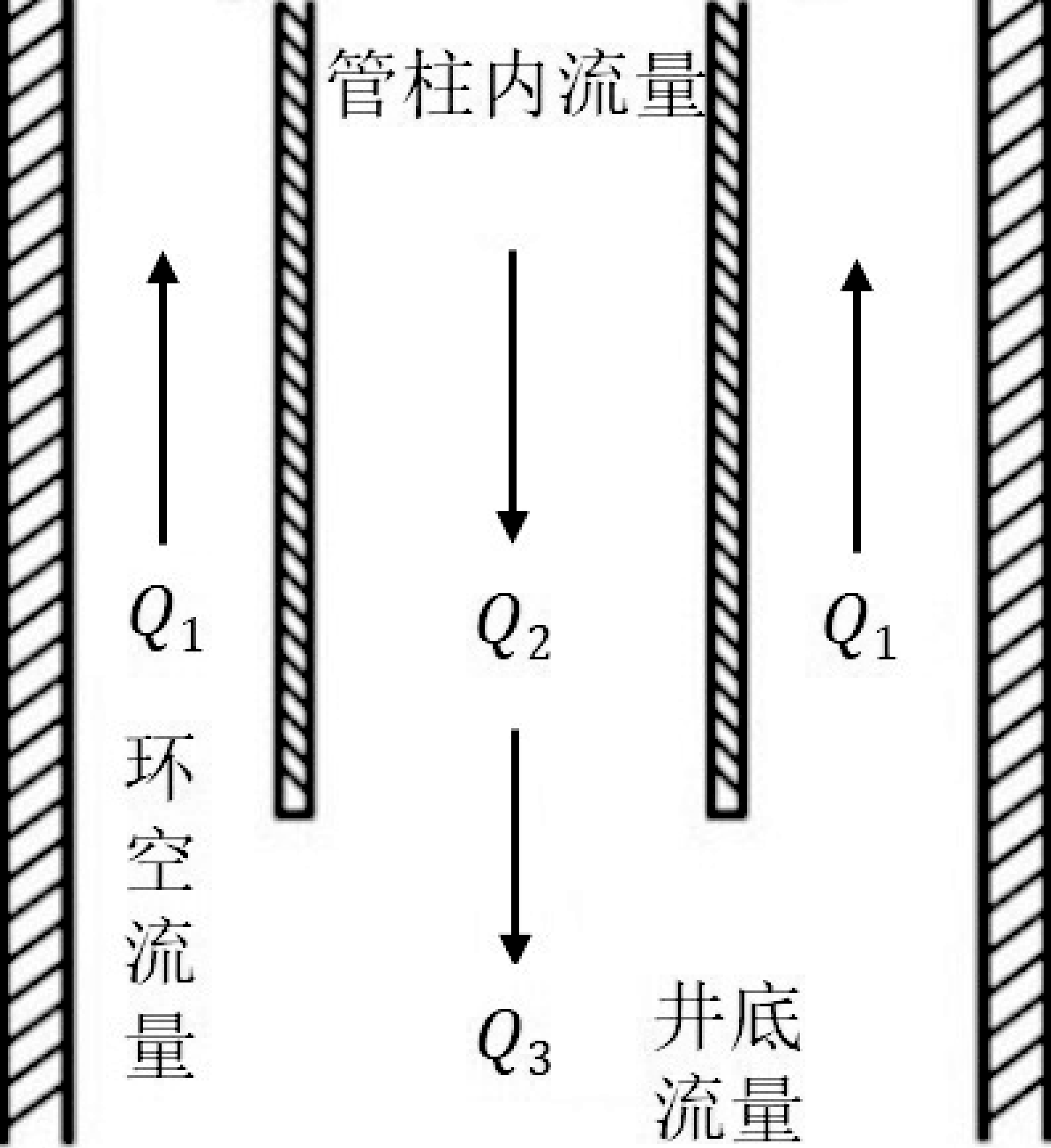
所谓“汇交点”，是指多流道流动时几条流道相交的一点。就井内流动来讲，环空流道、管柱内流道和井底流道汇交于管柱底部，此处即称为三流道的汇交点。若忽略汇交点处的局部压力损失，则在汇交点处各流道的瞬态压力都相同；另外，在汇交点处必须保持流动的连续性，这样就有了求解汇交点的两个条件。对于每条流道来讲，汇交点即为其边界点之一，故利用前述处理边界点的方法，对于n 路流道汇交点，可以得到n个特征方程，加上连续方程即有n+1个方程。忽略局部压力损失的汇交点有 n+1个未知量待求（即汇交点处的压力和n条流道各自的流量），如此就解决了汇交点的问题。
注水泥时，套管底端为开口管柱，井内的流动分为3个流道，汇交点模型如图5所示。
图5 汇交点模型示意图
有下面4个方程成立：

\{\begin{matrix} Q_{W} = Q_{W 1} - Q_{W 2} + Q_{W 3} \\ P_{W 1} = P_{S 1} + \frac{ρ_{S 1} C_{S 1}}{A_{S 1}} (Q_{W 1} - Q_{S 1}) + C_{S 1} Δ t P_{f S 1} \\ P_{W 2} = P_{R 2} - \frac{ρ_{R 2} C_{R 2}}{A_{R 2}} (Q_{W 2} - Q_{R 2}) - C_{R 2} Δ t P_{f R 2} \\ P_{W 3} = P_{S 3} + \frac{ρ_{S 3} C_{S 3}}{A_{S 3}} (Q_{W 3} - Q_{S 3}) + C_{S 3} Δ t P_{f S 3} \end{matrix}

(23)

解得：

\{\begin{matrix} K_{1} = \frac{A_{S 1} P_{S 1}}{ρ_{S 1} C_{S 1}} + \frac{A_{B 2} P_{B 2}}{ρ_{R 2} C_{R 2}} + \frac{A_{S 3} P_{S 3}}{ρ_{S 3} C_{S 3}} \\ K_{2} = \frac{A_{S 1} A t P_{S 31}}{ρ_{s 1}} - \frac{A_{R 2} A t P_{S R 2}}{ρ_{R 2}} + \frac{A_{s 3} A t P_{S 33}}{ρ_{s 3}} \\ P_{W 1} = P_{W 2} = P_{W 3} = \frac{Q_{W} - (Q_{S 1} - Q_{R 2} + Q_{S 3}) + K_{1} + K_{2}}{\frac{A_{S 1}}{ρ_{S 1} C_{s 1}} + \frac{A_{R 2}}{ρ_{R 2} C_{R 2}} + \frac{A_{S 3}}{ρ_{S 3} C_{s 3}}} \\ Q_{W 1} = \frac{A_{S 1}}{ρ_{S 1} C_{S 1}} (P_{W 1} - P_{S 1}) + Q_{S 1} - \frac{A_{S 1} Δ t P_{S 11}}{ρ_{S 1}} t \\ Q_{W 2} = \frac{A_{R 2}}{ρ_{R 2} C_{R 2}} (P_{R 2} - P_{W 2}) + Q_{R 2} - \frac{A_{R 2} Δ t P_{S R 2}}{ρ_{R 2}} \\ Q_{W 3} = \frac{A_{S 3}}{ρ_{S 3} C_{S 3}} (P_{W 3} - P_{S 3}) + Q_{S 3} - \frac{A_{S 3} Δ t P_{S 33}}{ρ_{S 3}} \\ Q_{W} = 0 t \end{matrix}

(24)

（4）连接点处理
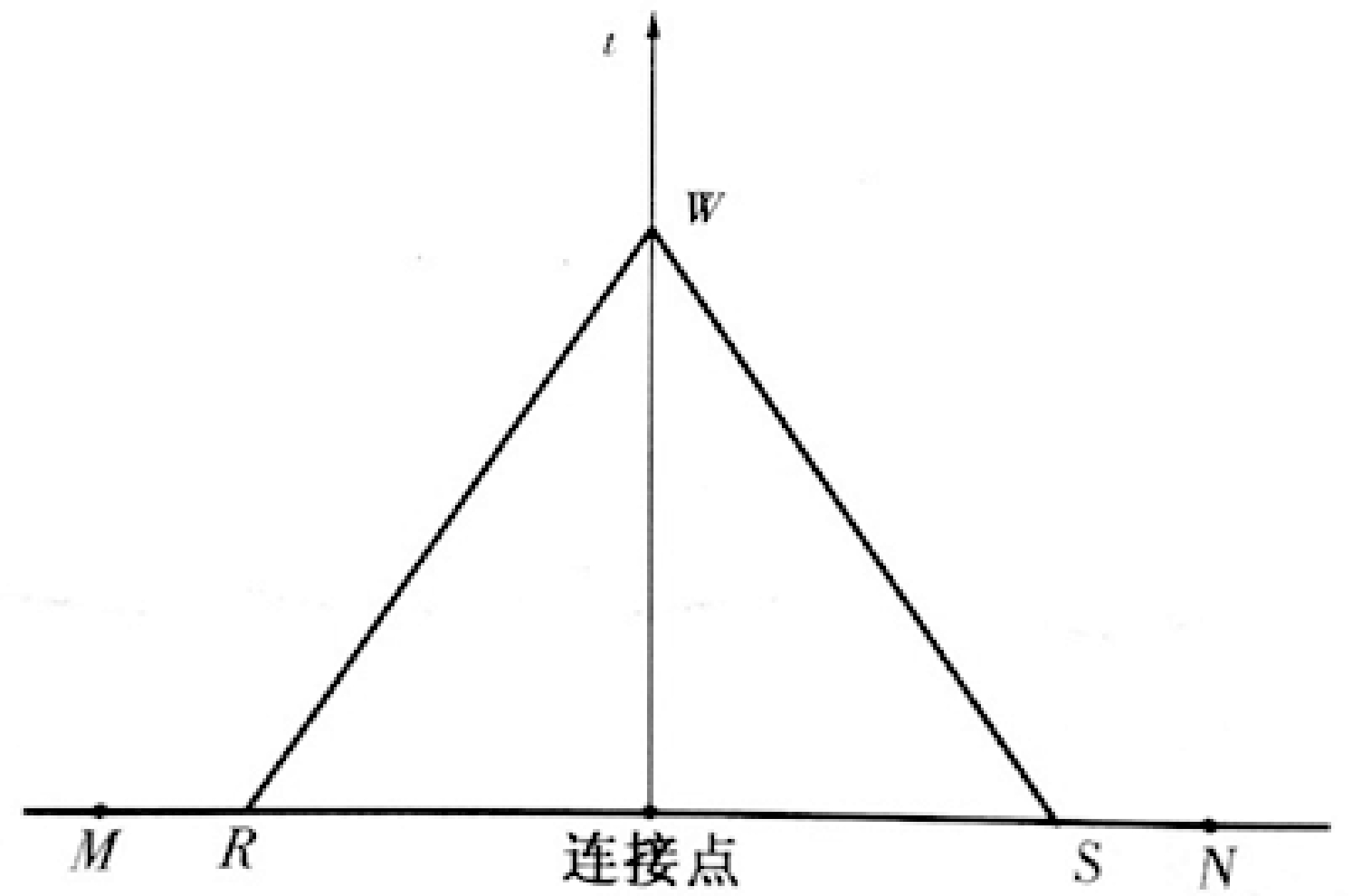
连接点由对接的两条流道组成，若忽略连接点处的局部压力损失，则两条流道在连接点处的压力和流量都相同。固井过程中，裸眼环空与套管环空的相连接处即为连接点（图6）。
图6 连接点模型示意图
对于向前特征线 RW 和向后特征线 SW 有特征方程：

\{\begin{matrix} P_{W} - P_{R} + \frac{ρ C_{R}}{A_{R}} (Q_{W} - Q_{R}) + C_{R} Δ t P_{f R} = 0 \\ - P_{W} + P_{S} + \frac{ρ C_{S}}{A_{S}} (Q_{W} - Q_{S}) + C_{S} Δ t P_{f S} = 0 \end{matrix}

(25)

解得：

Q_{W} = \frac{P_{R} - P_{S} + \frac{ρ C_{R} Q_{R}}{A_{R}} + \frac{ρ C_{S} Q_{S}}{A_{S}} - C_{R} Δ t P_{f R} - C_{S} Δ t P_{f R}}{\frac{ρ C_{R}}{A_{R}} + \frac{ρ C_{S}}{A_{S}}}

(26)

（5）流体密度与流道面积
设液体的压缩系数为 α，流道的膨胀系数为 β，则有

(27)

长管流动中考虑流体密度的变化与流道面积的变化
差分以上微分方程得：

ρ_{2} = \frac{4 ρ_{1}}{2 - α (p_{2} - p_{1})} - ρ_{1}

(28)

A_{2} = \frac{4 A_{1}}{2 - β (p_{2} - p_{1})} - A_{1}

(29)

注：下标 1代表上一时刻的物理量，下标 2代表下一时刻的物理量。
3 实例计算
3.1 计算基本数据
辽河油田某井二开技术套管下至 300 m，技术套管外径为 244.5 mm，壁厚为 10.36 mm，三开钻深 1000 m，裸眼段使用钻头直径为 215.9 mm，平均径井径扩大率 10%，钻井液密度 1.45 g/cm³，钻井液流性指数 0.65，稠度系数 0.3 Pa. sⁿ，套管外径 177.8 mm，套管壁厚10. 03 mm，水泥浆密度1.60 g/cm³，流性指数0.72，稠度系数0.4 Pa. sⁿ。根据上述建立的井筒压力计算方程，针对水泥返深至 100 m 时的固井泵关闭过程进行了计算分析。
3.2 关泵过程中井筒流量及压力计算与分析
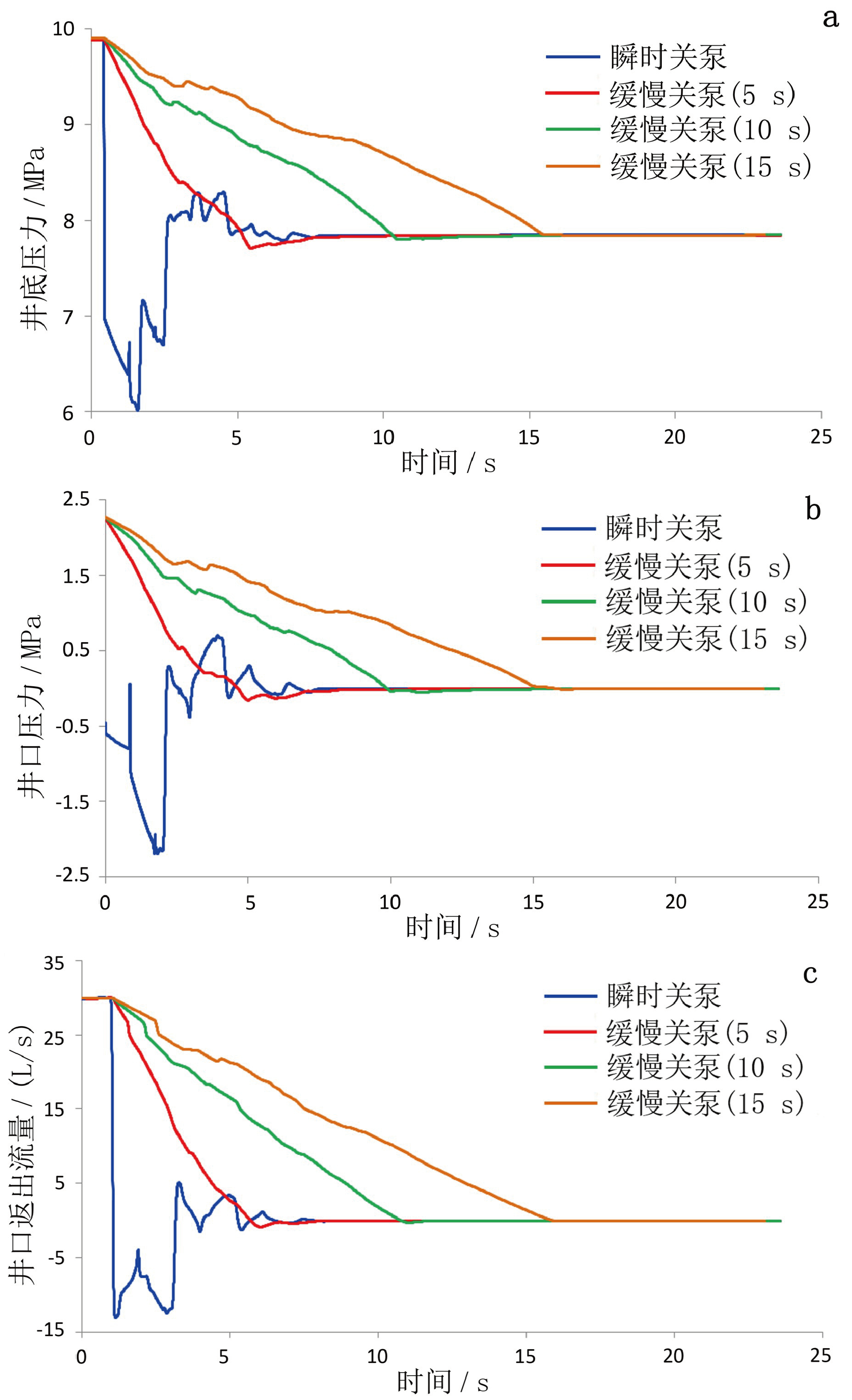
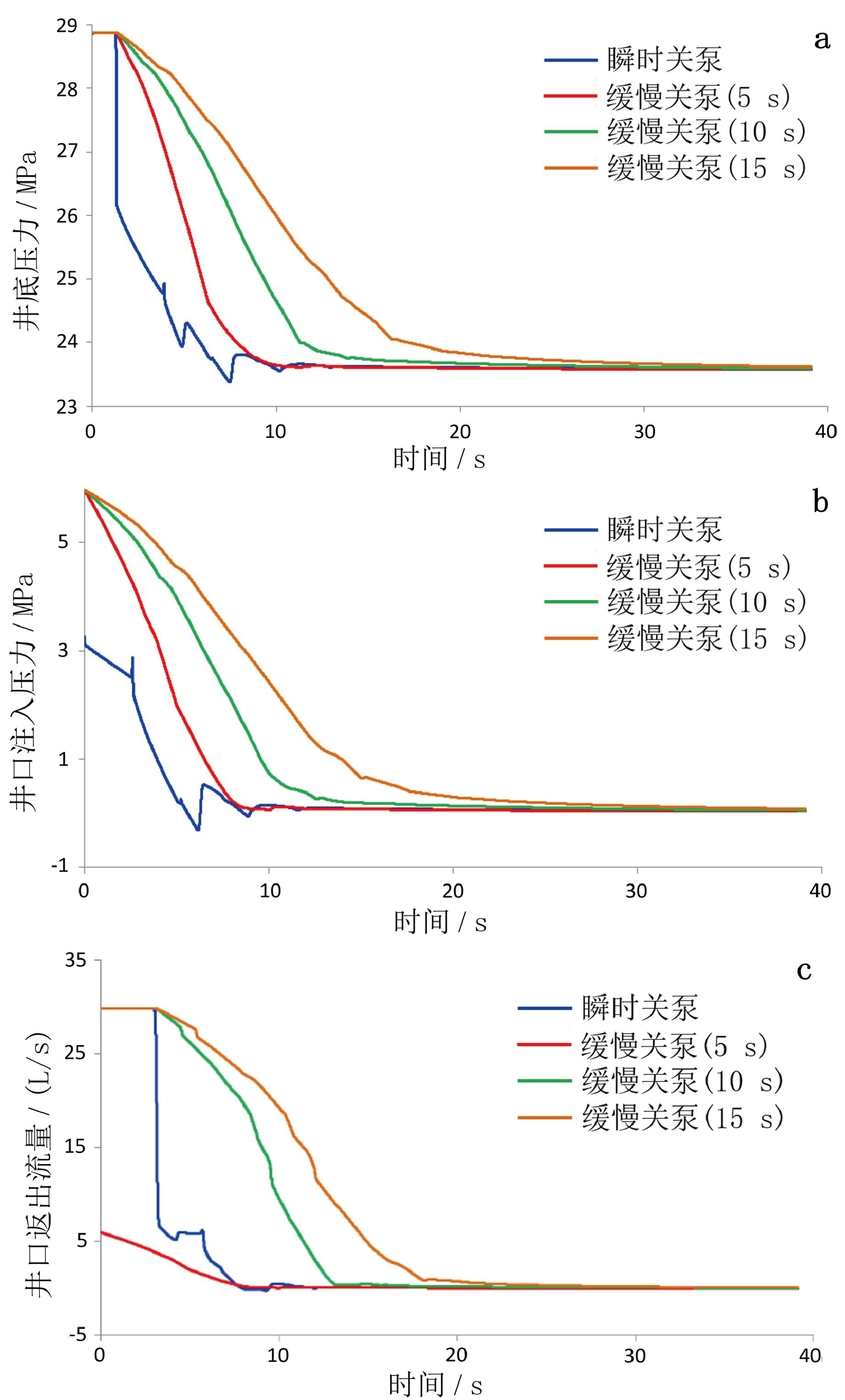
为了分析开泵方式在不同井深对井筒流量及压力的影响规律，设置了 4 种方式（瞬时关泵、缓慢关泵（5 s）、缓慢关泵（10 s）、缓慢关泵（15 s）），设置了 4 种井深（500 m、1000 m、1500 m、2000 m），分别模拟了 4种关泵方式、4种井深条件下井底压力、井口注入压力和环空返出排量的变化规律（图7~图10）。由计算结果可知，瞬时关泵对流量及压力的波动幅度影响最大，但最先达到稳定；缓慢关泵影响较小且关泵时间越长波动越平缓，但也越晚达到稳定。
图7 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（500 m）
为了得到更准确的规律，针对不同井深条件和不同关泵方式下的井底压力波动幅度、井口注入压力波动幅度、环空返出流量波动幅度进行了统计分析（金业权等，2013），分析结果分别见表1、表2、表3。
首先，固井瞬时关泵引发的井筒压力波动较大，从而容易引起事故（表1）。在井深为500 m条件下，瞬时关泵时井底最小压力可达 6. 01 MPa，比稳定后的井底压力 7.85 MPa 低 1.84 MPa，降幅达 23.44%，折合成压力当量密度为0.38 g/cm³；井深为 1000 m 条件下，瞬时关泵时井底最小压力可达 14.66 MPa，比稳定后的井底压力 15.66 MPa 低 1. 0 MPa，降幅达 6.39%，折合成压力当量密度为 0.1 g/cm³；因此，瞬时关泵方式引发的井筒压力波动不可忽视，在地层孔隙压力比较高的地层极容易引起井涌，甚至井喷，尤其是窄密度窗口地层会更为突出，这也是复杂气藏固井施工过程中气侵的原因之一。
图8 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（1000 m）
表1 关泵过程中井底压力波动幅度分析
注：P_bmin表示井底最小压力，P_bs表示稳定后的井底压力，η为波动幅度，无因次。
图9 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（1500 m）
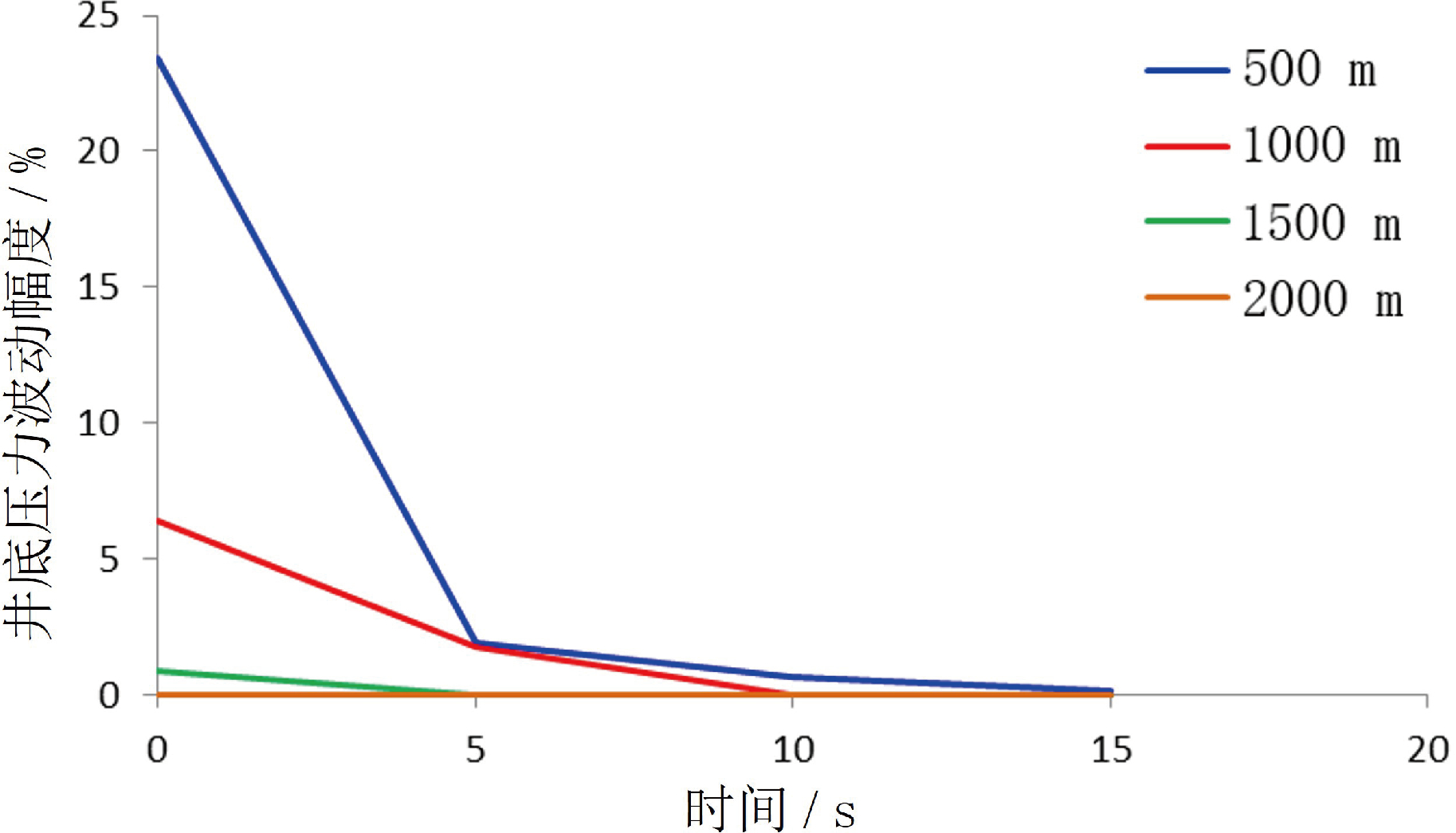
其次，在同一井深条件下，随着关泵时间的延长，井底压力波动幅度越来越小（表1，图11）。在 500 m 井深条件下，当关泵时间为 5 s 时，井底压力波动幅度为 1.91%，压力降幅为 0.15 MPa，折合成压力当量密度为 0. 03 g/cm³；当关泵时间为 10 s时，井底压力波动幅度为 0.64%，压力降幅为 0. 05 MPa，折合成压力当量密度为 0. 01 g/cm³；当关泵时间为 15 s 时，井底压力波动幅度为 0. 01 MPa，几乎可以忽略不计。因此，对于 500 m 井深的窄密度窗口气层来说，瞬时关泵和关泵时间为5 s仍然可能会诱发气侵，但对于一般地层来讲，发生气侵的几率较低。关泵时间超过 5 s 时，除非极窄密度窗口地层，一般不会诱发气侵。同理分析可得，当井深条件为 1000 m，瞬时关泵时压力当量密度降幅为 0.1 g/cm³，关泵时间为 5 s 时压力当量密度降幅为 0. 03g/cm³，对于 1000 m 井深的窄密度窗口气层来说，瞬时关泵和关泵时间为5 s仍然可能会诱发气侵，但对于一般地层来讲，发生气侵的几率较低；当关泵时间为 10 s和 15 s时，压力降幅为 0，对井底压力没有影响。进一步说明，在任何井深条件下，关泵时间越长，即关泵操作越缓慢，产生的井筒压力波动越小，井筒压力安全性越来越高。此外，在不同井深条件下，井深越大，关泵方式对井底压力影响越小，井深小于1000 m时，尽可能控制关泵时间不低于5 s （表1，图11）。井深条件为500 m和1000 m时，关泵时间在5 s以内产生的压力波动不可忽视；井深条件为1500 m和2000 m时，各种关泵方式条件下产生的井底压力波动均可忽略，这是由于井深越大，压力波沿井筒向下传播过程中被沿程阻力所消耗越多，到达井底已经很微弱甚至为 0。进一步说明，在井深条件为 1000 m 以内时，固井过程中应缓慢关泵，尽可能控制关泵时间不低于 5 s；在井深条件为 1000 m和1500 m时，关泵对井底压力没有影响，但应考虑井筒其他气层孔隙压力比较高的地层安全性。
图10 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（2000 m）
图11 不同井深条件下的井底压力波动幅度随关泵时间变化曲线
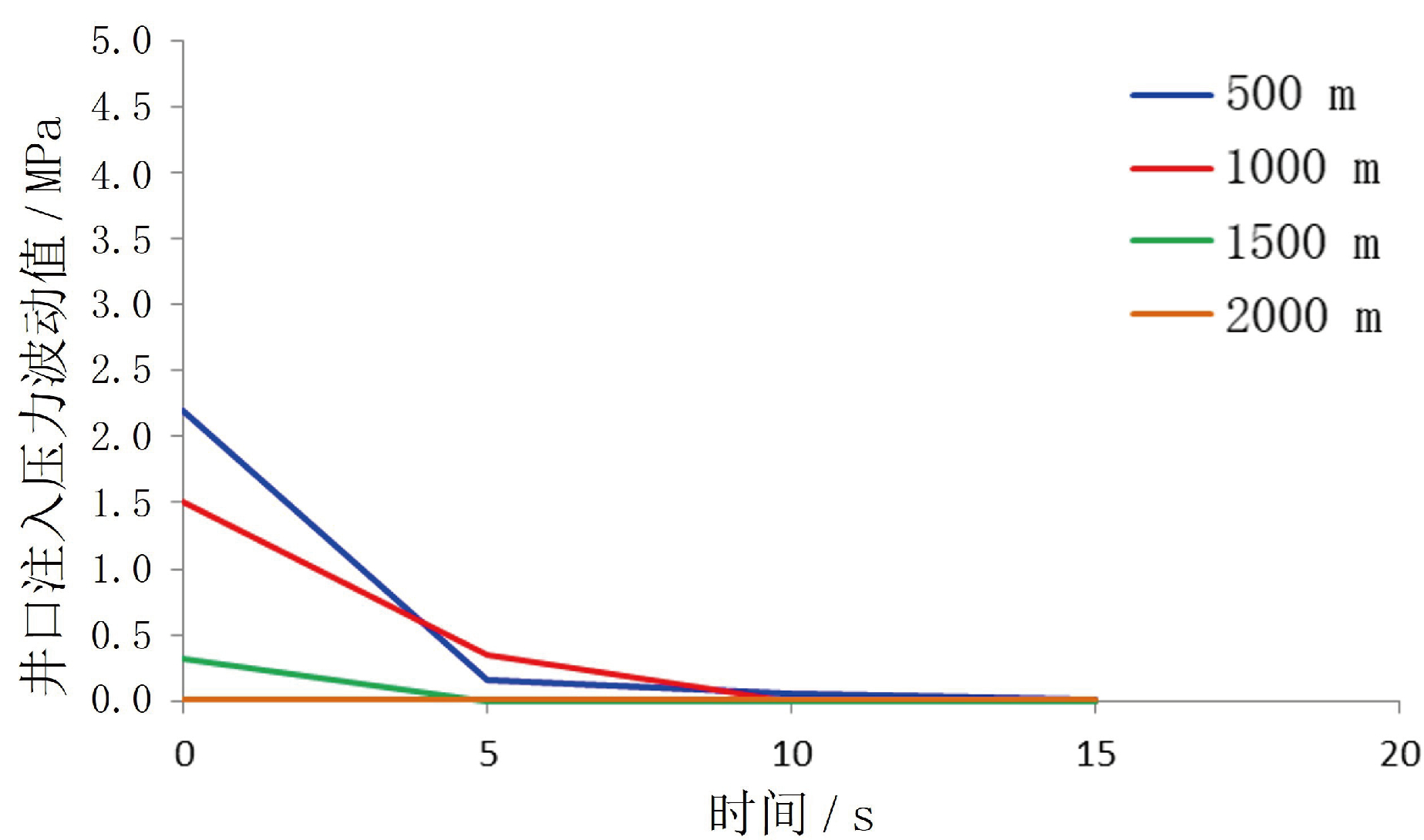
固井过程中关泵在井口也会形成压力波动（图7~图10）。其形成原因是注入流量突然减小产生的压力波沿井筒向下传播，在井底反射后又沿井筒向上传播至井口所致。从表2可以看出，井深为500 m 条件下，瞬时关泵时井口注入压力波动值可达2.19MPa（表中负值代表抽吸压力）；井深为 1000 m条件下，瞬时关泵时井口注入压力波动值可达1.51 MPa （表中负值代表抽吸压力）。
图12 不同井深条件下的井口注入压力波动幅度随关泵时间变化曲线
其次，在同一井深条件下，随着关泵时间的延长，井底压力波动值越来越小（表2，图12）。这是由于关泵操作越缓慢，流量变化越缓慢，产生的井筒压力波动越小，遇井底反射回来的井口压力波动也越来越小。
此外，在同一关泵方式条件下，随着井深的增加，井口注入压力波动值越来越小（表2，图12）。这是由于井深越大，压力波沿井筒向下传播和反射后向上传播的过程中被沿程阻力所消耗越多，到达井口时越来越小。
表2 关泵过程中井口注入压力波动幅度分析
注：P_wmin表示井口注入压力最小波动值，P_ws表示井口注入压力稳定后波动值，波动值为负值时代表抽吸压力。
表3 关泵过程中环空返出流量波动幅度分析
注：Q_min表示最小环空返出排量波动值，Q_s表示稳定后的环空返出排量波动值，波动值为负值时代表回流。
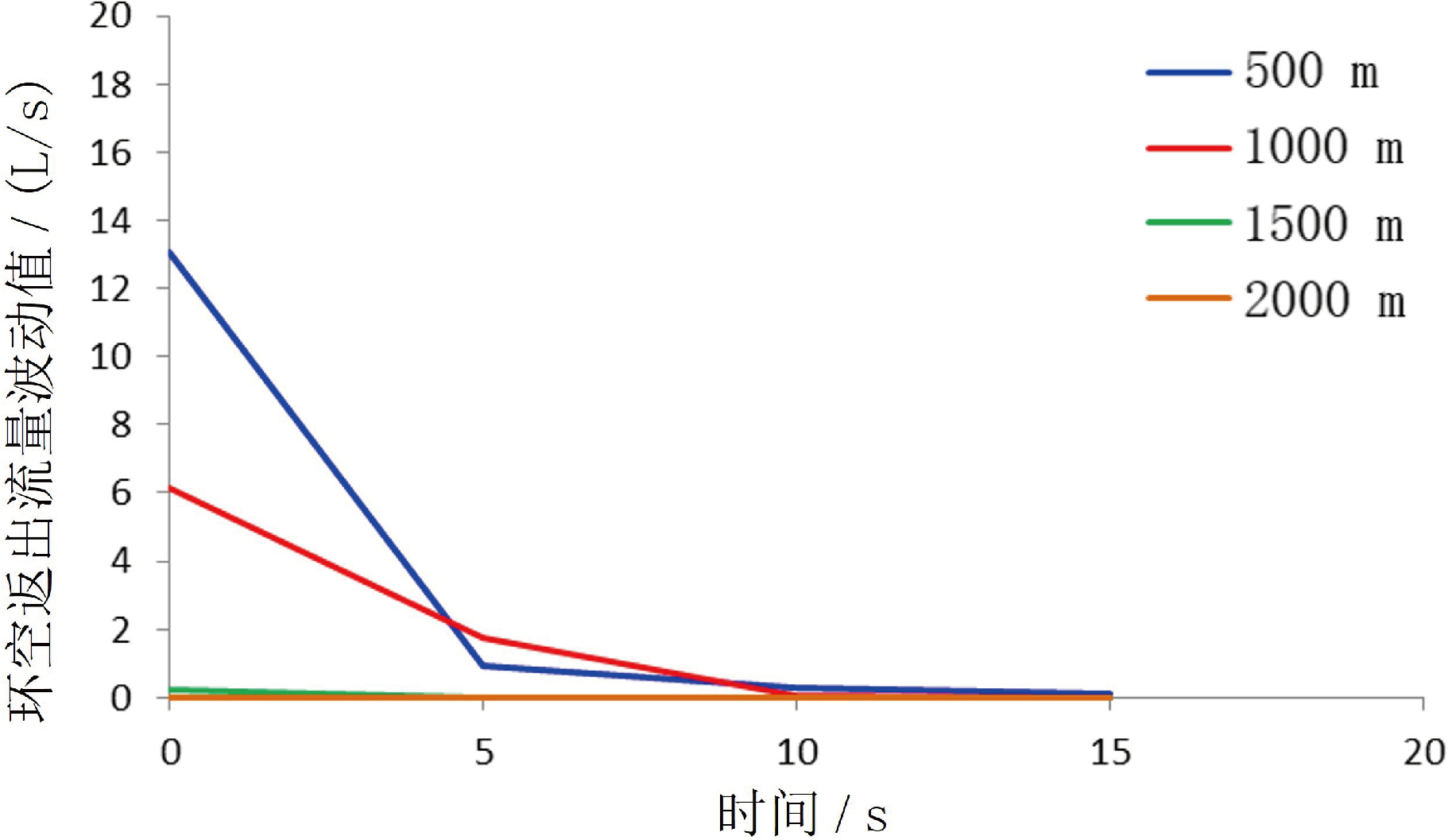
固井过程中关泵使环空返出排量也会形成波动（图7~图10）。其形成原因是流量突然减小形成的压力波沿井筒向下传播，在井底反射后又沿环空向上传播至井口所致，压力波导致排量的波动。从表3可以看出，井深为 500 m条件下，瞬时关泵时环空返出排量波动值可达 13. 04 L/s（表中负值代表回流）；井深为1000 m条件下，瞬时关泵时环空返出排量波动值可达6.12 L/s（表中负值代表回流）。在固井施工过程中，环空流体反复回流容易造成水泥浆与钻井液等流体掺混，影响其封固性能，因此应尽可能控制回流的产生。
图13 不同井深条件下的环空返出流量波动幅度随关泵时间变化曲线
在同一井深条件下，随着关泵时间的延长，环空返出排量波动值越来越小（表3，图13）。这是由于关泵操作越缓慢，产生的井筒压力波动越小，遇井底反射至环空的压力波动越来越小，从而导致环空返出排量波动越来越小。
在同一关泵方式条件下，随着井深的增加，环空返出排量波动值越来越小（表3，图13）。这是由于井深越大，压力波沿井筒向下传播和反射后沿环空向上传播的过程中被沿程阻力所消耗越多，到达井口时越来越小，从而导致环空返出排量波动越来越小。
4 结论
（1）本研究建立了固井泵关闭过程中的井筒流体流动控制方程，确定了求解方法和边界条件，形成了一套系统的井筒波动压力与流量计算方法。
（2）固井泵瞬时关闭对井筒压力、井口压力和环空流量都会产生不容忽视的波动影响，随着关泵时间的延长，井底压力、井口压力和环空流量波动幅度越来越小。为了保证固井施工安全和防止回流导致水泥浆掺混，优化关泵方式十分重要。
（3）随着井深的增大，关泵时间对井底压力、井口压力和环空流量波动的影响越来越小，这是由于压力波沿井筒向下传播和反射后向上传播的过程中被沿程阻力消耗越多所致，所以在浅井要更加关注关泵方式对井筒流动的影响。
注释
① Lal M.1983. Surge and Swab Modeling for Dynamic Pressures and Safe Trip Velcocities[R]. New Orleans： IADC/SPE Drilling Conference.
参考文献
- Lubinski A， Hsu F H， Nolte K G. 1997. Transient pressure surges due to pipe movement in an oil well［J］. Oil & Gas Science and Technology， 32（3）： 307‒348.
- Mitchell R F. 1988. Dynamic surge/swab pressure predictions［J］. SPE Drilling Engineering， 3（3）： 325‒333.
- 陈浩东，杨仲涵，李文拓，徐靖，刘裕，郑双进. 2021. 不同井斜角下的偏心环空固井顶替规律［J］. 矿产勘查， 12（9）： 1953‒1958.
- 樊洪海，褚元林. 1995. 起下钻时井眼内动态波动压力的预测［J］. 石油大学学报（自然科学版）， 19（5）： 36‒41.
- 郝俊芳. 1992. 平衡钻井与井控［M］. 北京：石油工业出版社， 33‒81.
- 金业权，孙泽秋，刘刚. 2013. 控压钻井液动节流压力控制系统仿真分析与试验研究［J］. 石油钻探技术， 41（2）： 109‒113.
- 孔祥伟，林元华，邱伊婕. 2014a. 控压钻井中两步关阀阀芯所受瞬变压力研究［J］. 应用力学学报， 31（4）： 20‒24.
- 孔祥伟，林元华，邱伊婕. 2014b. 微流量控压钻井中节流阀动作对环空压力的影响［J］. 石油钻探技术， 42（3）： 22‒26.
- 孔祥伟，林元华，邱伊婕，郑双进. 2015. 钻井泥浆泵失控/重载引发的波动压力［J］. 石油学报， 36（1）： 114‒119.
- 刘刚，蒲家宁. 2003. 瞬变流摩阻计算及摩阻对水力瞬变的影响［J］. 力学与实践， 25（1）： 13‒15.
- 刘竹溪，刘光临. 1988. 泵站水锤及其防护［M］. 北京：电力出版社， 63‒79.
- 栾鸿儒. 1993. 水泵及水泵站［M］. 北京：中国水利水电出版社.
- 栾鸿儒，杨晓东. 1987. 逆止阀旁通管消减停泵水锤的研究和计算［C］//中国机械工程学会流体工程学会泵专业学术讨论会. 陕西：陕西机械学院， 27.
- 庞东豪，陈彬，赵维青，赵苏文，严德，郑双进. 2022. 密度差与水泥浆流变参数耦合的水平井固井顶替规律研究［J］. 矿产勘查， 13（2/3）： 302‒308.
- 孙秀芳. 2001. 污水泵站水锤计算与缓闭止回阀的应用［J］. 中国给水排水， 17（8）： 48‒49.
- 唐晓寅，叶江涛. 2004. 长管水击最大水击压强的解析［J］. 后勤工程学院学报， 20（2）： 32‒36.
- 王立辉. 2020. 井筒压力波动条件下钻井液侵入煤岩实验研究［J］. 矿产勘查， 11（2）： 384‒389.
- 魏纳，孟英峰，李皋，徐小峰，王在明，杨辉. 2013. 套管阀关阀井下压力动态演变规律的研究［J］. 应用力学学报， 30（3）： 412‒416.
- 张迎进，朱忠喜，蔡敏，尚可心. 2008. 钻井泵开启和关闭瞬时水击压力计算［J］. 石油钻探技术， 36（2）： 48‒50.

图1 井筒内流道微元示意图

图2 流体运动微元示意图

图3 特征线图

图4 方网格加插值方法示意图

图5 汇交点模型示意图

图6 连接点模型示意图

图7 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（500 m）

图8 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（1000 m）

图9 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（1500 m）

图10 井底压力（a）、注入压力（b）及返出排量（c）随关泵时间变化曲线（2000 m）

图11 不同井深条件下的井底压力波动幅度随关泵时间变化曲线

图12 不同井深条件下的井口注入压力波动幅度随关泵时间变化曲线

图13 不同井深条件下的环空返出流量波动幅度随关泵时间变化曲线

表1 关泵过程中井底压力波动幅度分析

表2 关泵过程中井口注入压力波动幅度分析

表3 关泵过程中环空返出流量波动幅度分析

相似文献

基本信息

中图分类号: TE256
文献标识码: A
DOI: 10.20008/j.kckc.202405020
文章编号: 1674-7801(2024)05-0884-10

基金信息

本文受国家自然科学基金项目“不规则井眼固井环空流场及井壁附着泥浆滞留机理研究”（51804043）资助；

引用信息

韩加帆，郑双进，魏君陶. 2024. 固井泵关闭过程中的井筒流体流动特性研究［J］. 矿产勘查，15（5）：884-893.

Han Jiafan，Zheng Shuangjin，Wei Juntao. 2024. Research on the fluid flow characteristics in the process of closing pump in cementing［J］. Mineral Exploration，15（5）：884-893.

稿件历史

收稿日期: 2023-08-31

参考文献

Lubinski A， Hsu F H， Nolte K G. 1997. Transient pressure surges due to pipe movement in an oil well［J］. Oil & Gas Science and Technology， 32（3）： 307‒348.
Mitchell R F. 1988. Dynamic surge/swab pressure predictions［J］. SPE Drilling Engineering， 3（3）： 325‒333.
陈浩东，杨仲涵，李文拓，徐靖，刘裕，郑双进. 2021. 不同井斜角下的偏心环空固井顶替规律［J］. 矿产勘查， 12（9）： 1953‒1958.
樊洪海，褚元林. 1995. 起下钻时井眼内动态波动压力的预测［J］. 石油大学学报（自然科学版）， 19（5）： 36‒41.
郝俊芳. 1992. 平衡钻井与井控［M］. 北京：石油工业出版社， 33‒81.
金业权，孙泽秋，刘刚. 2013. 控压钻井液动节流压力控制系统仿真分析与试验研究［J］. 石油钻探技术， 41（2）： 109‒113.
孔祥伟，林元华，邱伊婕. 2014a. 控压钻井中两步关阀阀芯所受瞬变压力研究［J］. 应用力学学报， 31（4）： 20‒24.
孔祥伟，林元华，邱伊婕. 2014b. 微流量控压钻井中节流阀动作对环空压力的影响［J］. 石油钻探技术， 42（3）： 22‒26.
孔祥伟，林元华，邱伊婕，郑双进. 2015. 钻井泥浆泵失控/重载引发的波动压力［J］. 石油学报， 36（1）： 114‒119.
刘刚，蒲家宁. 2003. 瞬变流摩阻计算及摩阻对水力瞬变的影响［J］. 力学与实践， 25（1）： 13‒15.
刘竹溪，刘光临. 1988. 泵站水锤及其防护［M］. 北京：电力出版社， 63‒79.
栾鸿儒. 1993. 水泵及水泵站［M］. 北京：中国水利水电出版社.
栾鸿儒，杨晓东. 1987. 逆止阀旁通管消减停泵水锤的研究和计算［C］//中国机械工程学会流体工程学会泵专业学术讨论会. 陕西：陕西机械学院， 27.
庞东豪，陈彬，赵维青，赵苏文，严德，郑双进. 2022. 密度差与水泥浆流变参数耦合的水平井固井顶替规律研究［J］. 矿产勘查， 13（2/3）： 302‒308.
孙秀芳. 2001. 污水泵站水锤计算与缓闭止回阀的应用［J］. 中国给水排水， 17（8）： 48‒49.
唐晓寅，叶江涛. 2004. 长管水击最大水击压强的解析［J］. 后勤工程学院学报， 20（2）： 32‒36.
王立辉. 2020. 井筒压力波动条件下钻井液侵入煤岩实验研究［J］. 矿产勘查， 11（2）： 384‒389.
魏纳，孟英峰，李皋，徐小峰，王在明，杨辉. 2013. 套管阀关阀井下压力动态演变规律的研究［J］. 应用力学学报， 30（3）： 412‒416.
张迎进，朱忠喜，蔡敏，尚可心. 2008. 钻井泵开启和关闭瞬时水击压力计算［J］. 石油钻探技术， 36（2）： 48‒50.

分享给微信好友或者朋友圈

使用微信“扫一扫”功能。

固井泵关闭过程中的井筒流体流动特性研究

Research on the fluid flow characteristics in the process of closing pump in cementing

摘要

Abstract

关键词

Keywords

0 引言

1 井筒流体流动控制方程

1.1 连续性方程

(1)

1.2 运动方程

(2)

2 求解方法与边界条件

2.1 求解方法

(3)

(4)

(5)

(6)

(8)

(10)

(11)

(12)

(13)

(14)

2.2 边界条件

(15)

(16)

(17)

2.3 多流道计算方法

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

3 实例计算

3.1 计算基本数据

3.2 关泵过程中井筒流量及压力计算与分析

4 结论

参考文献

相似文献

基本信息

基金信息

引用信息

稿件历史

参考文献