0 引言

资源是国际上主要关注的社会问题，与环境、人口问题具有同等地位。矿产资源是有限、不可再生的自然资源，是推动工业化进程的主要支撑资源 （张龙正，2020）。随着工业化进程的逐渐加快，矿产资源需求呈现急剧增加的趋势，如何有效开发与利用矿产资源成为国家重点研究课题之一，也是维持国民经济可持续发展的关键所在。依据统计数据可知，中国能源（95%）、工业原料（80%）、农业生产资源（70%）、饮用水（30%）等均来源于矿产资源及其地下水资源。中国矿产资源总量较为丰富，但矿产资源勘查、开发难度较大，成为抑制矿产行业及其经济发展的主要挑战之一。

近年来，浅表矿产资源数量逐渐减少，矿产资源开发难度逐渐加大，深部矿产资源找寻成为矿产勘查的重点。以往矿产勘查主要应用二维地质信息资料，例如柱状图、平面地质图、剖面图等，这些信息资料需要专业人员进行解释与说明，但依然无法从整体角度把握复杂地质情况，致使矿产勘查效果较差（商晓飞等，2022）。随着矿产找寻深度增加，有利地质信息获取数量逐渐减少，三维地质建模技术的出现为深部矿产资源勘查与开发带来了新的希望与手段支撑，其能够根据高程数据、地质资料与钻孔数据构建三维地质模型，清晰地展示矿床深部情况，为矿产勘查提供极大的便利，满足社会矿产资源的需求。因此，本文提出基于地质三维建模的矿床蚀变带深部资源预测方法研究，希望通过地质三维建模技术的应用，提升矿床蚀变带深部资源预测的精度，为矿床的有效开发提供助力。

1 矿床蚀变带深部资源预测方法研究

1.1 矿床蚀变带深部地质三维模型构建

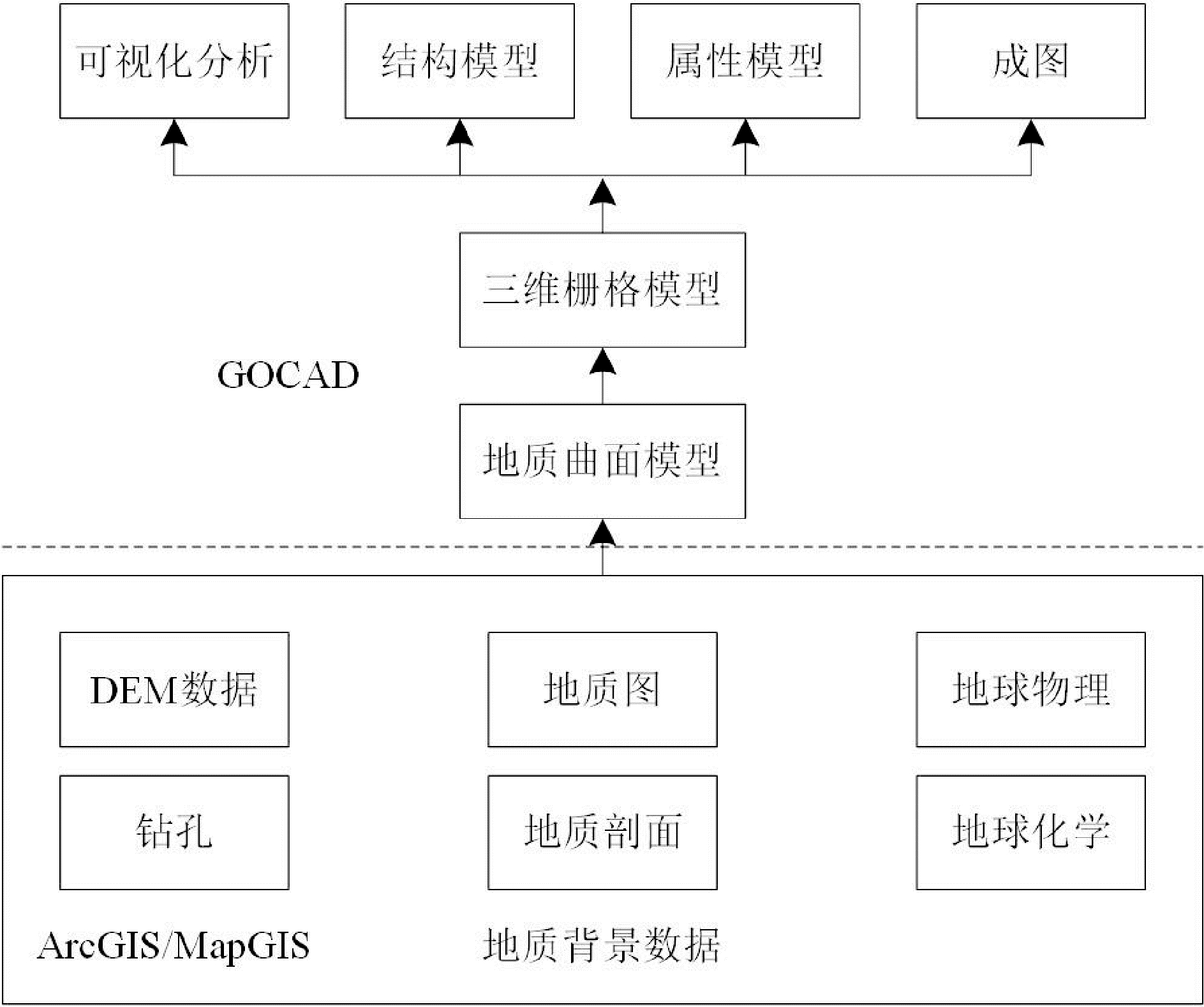
应用ArcGIS、MapGIS等地学软件处理收集的矿床地层深部地质信息资料，融合遥感、地质、工程、地球化学等数据，结合地质三维建模软件（GOCAD） 与计算机技术，构建矿床蚀变带深部地质三维模型，构建流程如图1所示。

如图1 所示，依据多源矿床蚀变带深部地质数据，应用倾角与倾向构建地质曲面模型，采用断层法向量表示，表达式为：

式（1）中，$\overrightarrow{N}$表示的是断层法向量，即为地质曲面模型；α^o 表示的是地质曲面对应倾角；β^o表示的是地质曲面对应倾向。

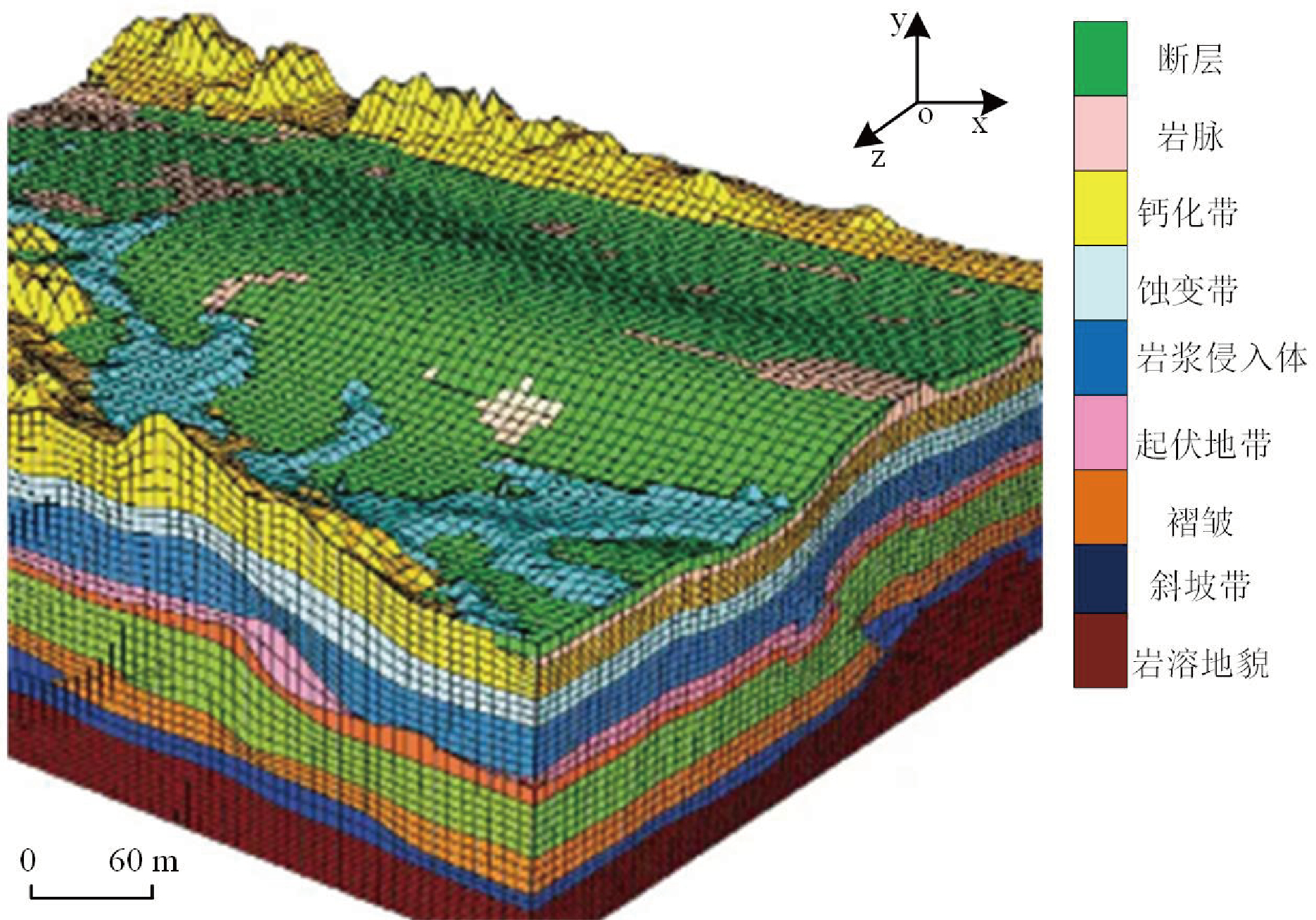
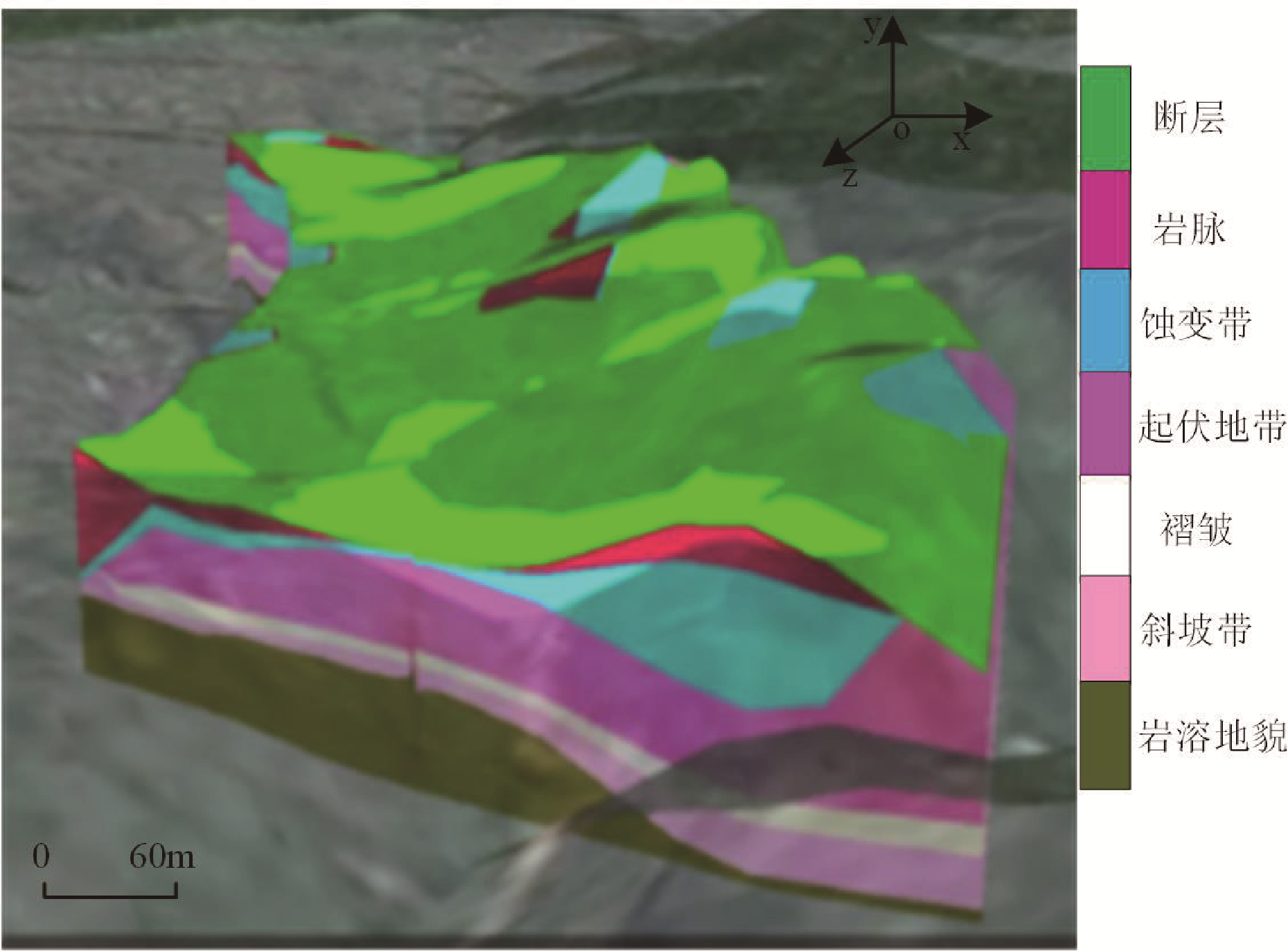
地质曲面模型只能显示矿床地层深部地质空间形态信息，无法反映矿床深部地质之间的逻辑关系与属性信息。因此，基于地质曲面模型创建三维栅格模型（郝英红等，2021；周昊等，2022），即矿床蚀变带深部地质三维模型（图2）。

上述过程完成了矿床蚀变带深部地质三维模型的构建，反映蚀变带深部地质的全部信息（李成文等，2022；张琪彬等，2023），可为后续深部资源预测的实现奠定坚实的基础。

1.2 矿床蚀变带深部地质统计单元划分

以上述构建的矿床蚀变带深部地质三维模型为基础，为了方便研究的进行，提升深部资源预测的精度，划分矿床蚀变带深部地质统计单元，并对最佳单元尺度进行估计，为后续地质变量的提取与赋权提供一定的支撑（李朋伟等，2021）。

常规情况下，地质统计单元划分尺度由地质构造信息值（区域地层、地质特征、资源量估算结果等）与累计块体体积共同决定，两者之间服从幂律关系，表达式为：

式（2）中，v 表示的是累计块体体积（m³）；χ₀ 表示的是辅助参数（渗透系数、含水层厚度、水位降深等），取值范围为[ 0，1]；f 表示的是地质构造有力信息值；d表示的是分维数，反映着矿床蚀变带深部地质三维模型划分的复杂程度。

矿床蚀变带深部的地质块体通常具有不同的尺度，包括小于1 m的细节结构、数十米至数百米的中等尺度构造，以及更大的地块。这些地质块体的尺度与其分维数之间存在一定的关系。

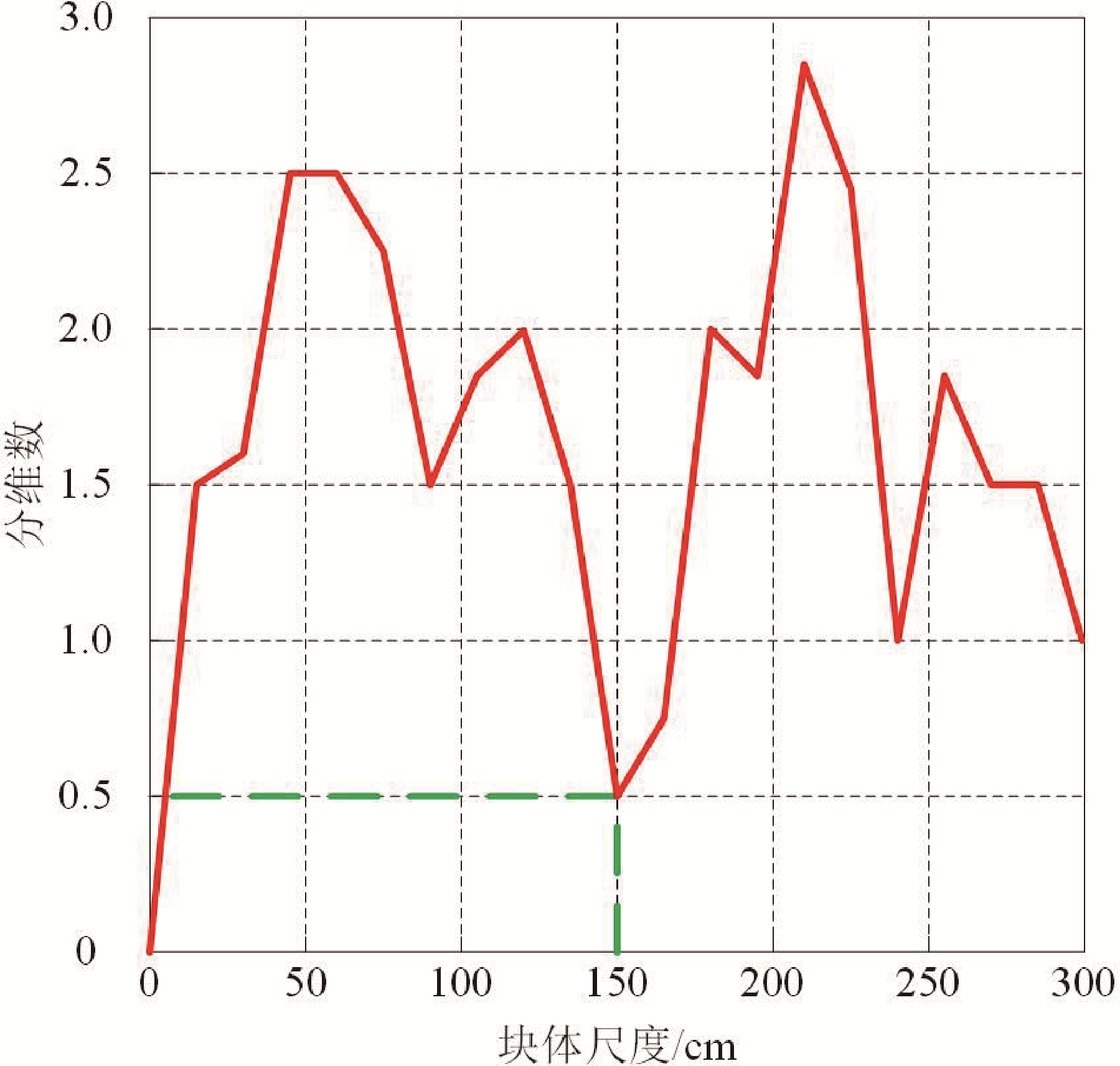
分维数是描述一个物理或几何对象几何特征的参数之一，可用于表征该对象的复杂度和几何结构。对于矿床蚀变带深部的地质块体，其分维数通常可以通过分形分析的方法进行计算。这种尺度依赖的分维数变化特征表明矿床蚀变带深部的地质块体呈现出分形特征，并且在不同尺度下具有不同的复杂性和几何结构。因此，通过块体尺度计算分维数可以为矿床蚀变带深部资源的预测提供重要的参考依据。块体尺度即为矿床蚀变带深部地质统计单元，其与分维数之间的关系如图3所示。

如图3所示，当块体尺度取值为150 cm时，分维数取值达到最小值 0.5，有利于后续研究的进行。因此，确定矿床蚀变带深部地质统计单元最佳尺度为 150 cm，设置统计划分单元形状为正方体（刘子杰等，2020；张庆贺等，2022）。

依据上述确定的最佳单元尺度对矿床蚀变带深部地质进行统计划分，由于研究篇幅有限，此处不对划分结果进行详细展示（高海东等，2020；赵子欧等，2020；俞嘉嘉等，2021；陈军等，2022），为后续地质变量提取及其赋权做好充足的准备。

1.3 矿床蚀变带深部地质变量提取与赋权

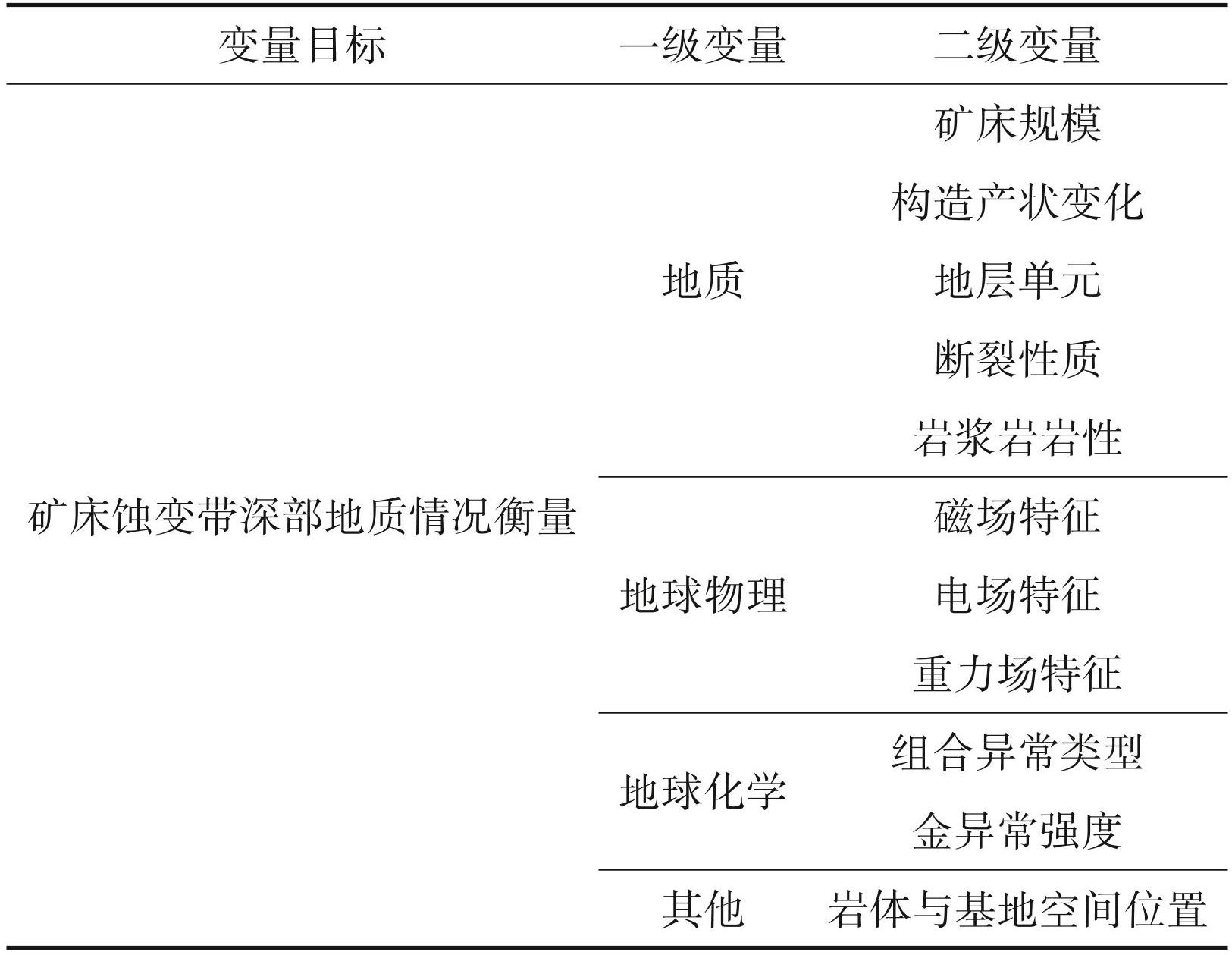
以矿床蚀变带深部地质统计单元划分结果为依据，依据典型性、普适性、独立性、随机性等原则提取矿床蚀变带深部地质变量，并对其赋权数值进行确定，为最终深部资源预测提供便利（李杰等， 2021；林寿洪，2021；刘彦良等，2021）。矿床蚀变带深部地质统计单元变量提取结果如表1所示。

如表1 所示，选取的地质变量对深部资源预测的影响程度存在着较大的差别，故基于状态变权向量构造地质变量的权函数，以此为基础，实现地质变量的赋权（周邓等，2022）。地质变量权函数表达式为：

式（3）中，ω_j表示的是第 j个地质变量对应的权重系数；δ_j（r_j）表示的是地质变量r_j对应的状态变权向量中的第j个分量；m表示的是地质变量的总数量。

通过式（3）可知，地质变量权函数是以状态变权向量为基础的，如何对其进行准确获取，对地质变量赋权至关重要（李海文和鲍学英，2021）。状态变权向量计算公式为：

式（4）中，$F\left(\frac{r_j}{\zeta }\right)$表示的是实际需要函数，具体形式需要根据矿床蚀变带深部地质具体情况进行设置；ζ表示的是状态变权向量获取辅助因子。

上述过程完成了矿床蚀变带深部地质统计单元变量的提取与赋权，可以将深部资源转化为变量形式，方便后续深部资源的预测。

1.4 矿床蚀变带深部资源预测

以上述提取与赋权的地质变量为基础，探究深部地质统计单元之间的联系度，以此为基础，基于三维证据权法预测矿床蚀变带深部资源，为分析地质特征及找矿方向提供助力（耿瑞瑞等，2021）。

深部地质统计单元联系度是以有矿统计单元为核心，计算其他单元与其之间的联系度，依据计算联系度对统计单元进行分级。联系度计算公式为：

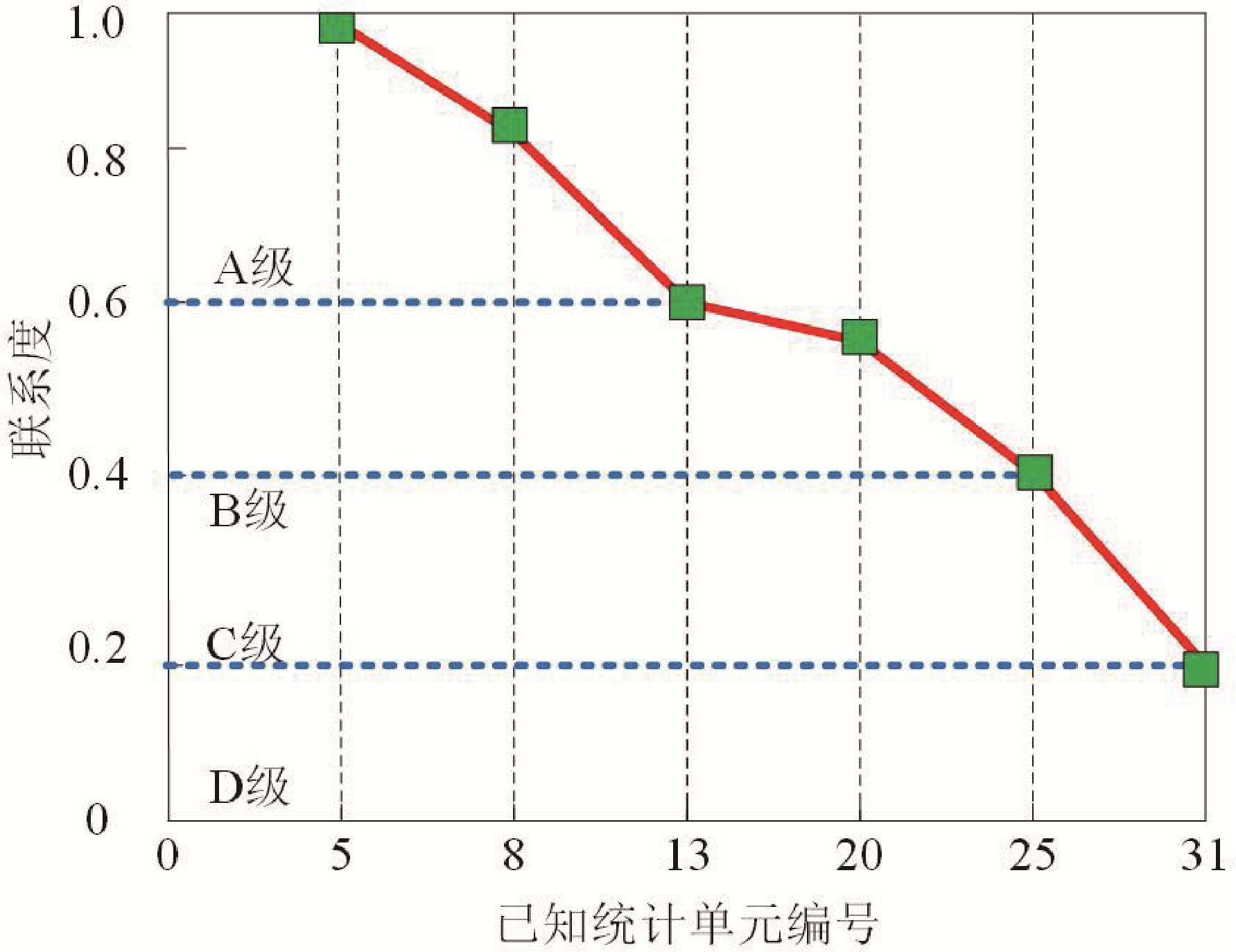
式（5）中，L_ij表示的是有矿统计单元v_i与未知统计单元v_j之间的联系度；n表示的是统计单元的总数量；${\omega }_{v_j}$表示的是未知统计单元 v_j的地质变量综合赋权；D_ij表示的是统计单元 v_i与 v_j的距离（m）；ψ₀表示的是单位联系度数值；ε″表示的是误差项，可以有效降低联系度计算的误差。依据联系度对统计单元进行分级，具体分级原则如图4所示。

如图4 所示，当不同统计单元的联系度变化呈现放缓状态与急速下降状态相结合的趋势时，可根据该趋势内的联系度将对应的统计单元划分为一个等级。由此可知，当联系度 L_ij 在（0.60，1. 00]范围内，将统计单元划分为 A 级单元；当联系度 L_ij 在（0.40，0.60]范围内，将统计单元划分为 B 级单元； 当联系度 L_ij 在（0.20，0.40]范围内，将统计单元划分为 C 级单元；当联系度 L_ij在[ 0. 00，0.20]范围内，将统计单元划分为 D 级单元。其中，A 级单元存在矿产资源概率最大，D 级单元存在矿产资源概率最小。

以深部地质统计单元分级结果为基础，应用三维证据权法确定每个统计单元的矿产资源存在概率，表示为：

式（6）中，$\widehat{P}$表示的是深部地质统计单元矿产资源存在概率；P₁ 与 P₂ 表示的是先验概率与后验概率；P₂通过指数函数，以P₁和ω_j为底，对地质变量相关系数进行求和运算，以此得到后验概率；S_D 表示的是矿体面积（m²）；S_T 表示的是统计单元标准面积（m²）。

以式（6）计算结果为基础，确定矿床蚀变带深部资源预测方程表达式为：

式（7）中，H表示的是矿床蚀变带深部资源预测结果（石勇和史秀志，2021）；H₀ 表示的是矿产资源单位数值。

通过上述过程获取了矿床蚀变带深部资源预测结果，为矿床开发计划的制定提供有效的数据支撑。

2 实验与结果分析

2.1 实验对象选取

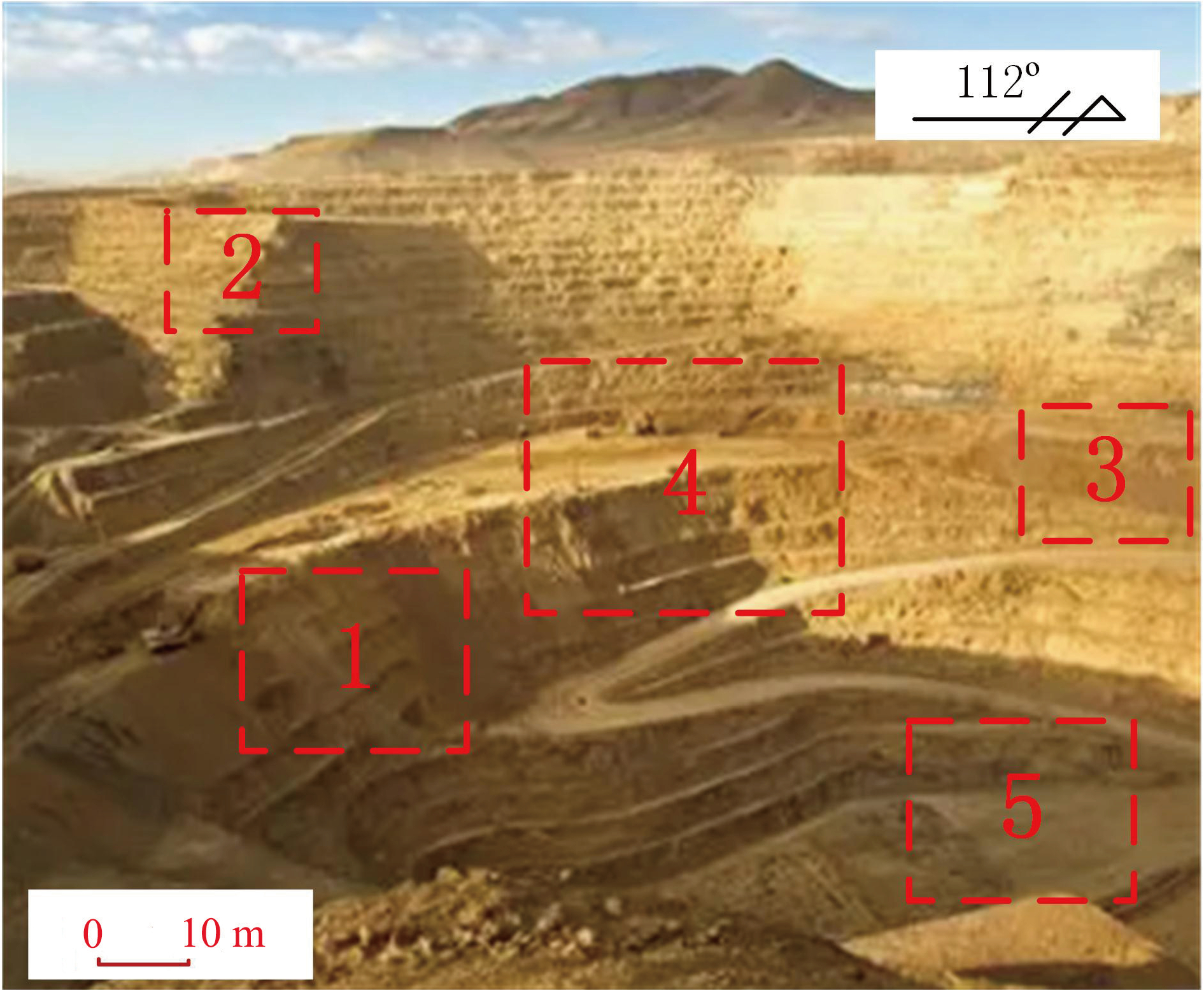
选取某支脉北缘矿床作为实验对象。该地区地形山势陡峻，海拔一般为 3800~4500 m，最高 4930 m，平均海拔 4200 m。区内共发现铜多金属矿化带 6 条，黄铁矿化、褐铁矿化蚀变带 2 条；圈定铜多金属矿体 41 个。其中主矿体 3 个：M1-2、M2-1、 M3-1。矿体（Cu）平均品位分别为 1.32×10^-2、0.93×10^-2、1.10×10^-2。山区覆盖相对较厚，多为碎石、残坡积及少量风成黄土组成，结合图1 矿床蚀变带深部地质三维模型构建流程图中应用ArcGIS、MapGIS 等地学软件处理收集矿床地层深部地质信息资料的内容，根据地质背景数据中的二级矿床规模将实验对象划分为5个区域，其具体情况如图5所示。

如图5所示，选取的实验矿床正处于开采阶段，浅表矿产资源已经开采完成，而深部资源的具体情况仍然未知，是矿床继续开采的最大难题。

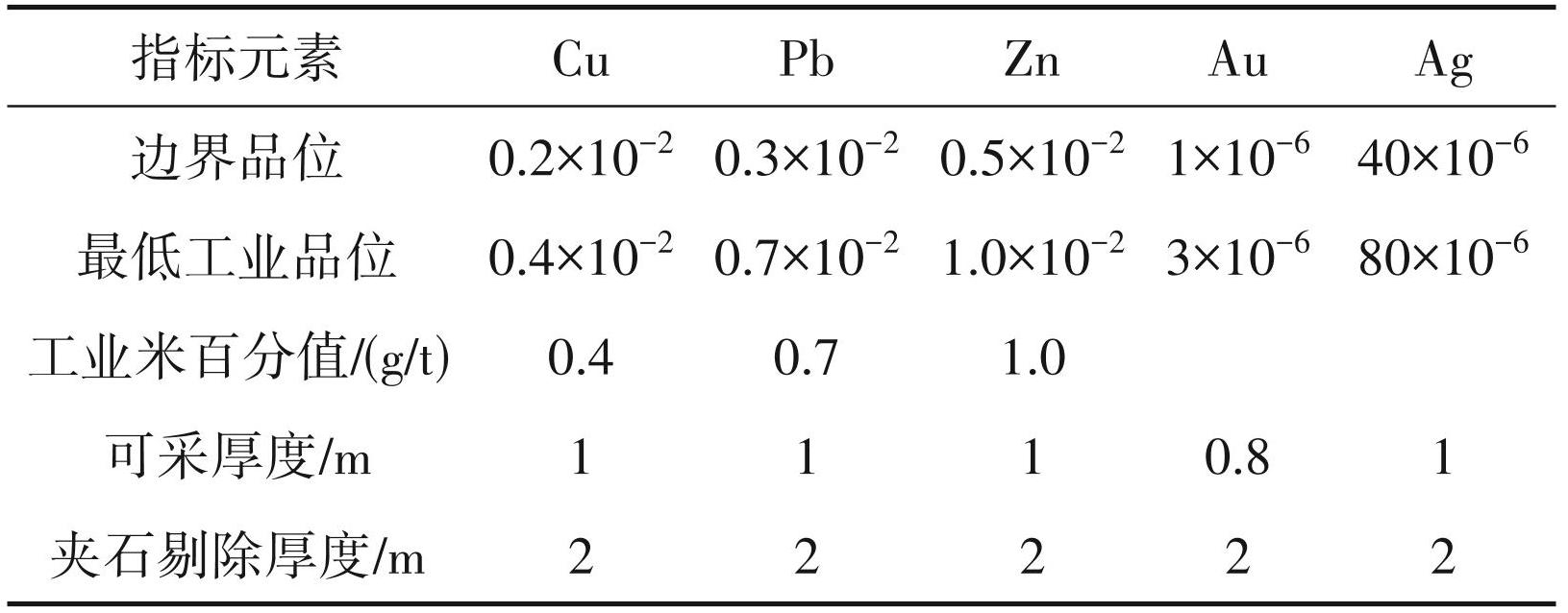
资源量估算采用的工业指标和伴生有用组分综合利用指标是依据《铜、铅、锌、银、镍、钼矿地质勘查规范》（DZ/T 0214-2002）与《岩金矿地质勘查规范》（DZ/T 0205-2002）相关参考指标。以矿区现有资料看，矿床主要成矿元素为铜、铅、锌，伴生有用组分为银，矿床规模为小型矿床。资源量估算采用的工业指标及伴生组分评价指标如表2所示。

为了提升提出方法应用性能验证的精准性，在矿床随机选取 5 个区域作为实验对象，并将其编号为1~5，实验区域规模大小不同，符合提出方法应用性能测试需求。

2.2 地质变量处理与赋值

提出方法选取了多个地质变量为深部资源预测的指标，其包含定性变量与定量变量，量纲存在着较大的不同，取值范围与标准也具有较大的差距，是降低实验效率的关键因素。因此，在实验进行之前，对地质变量进行处理与赋值，方便后续实验的进行。地质变量量纲统一处理公式为：

式（8）中，r'_j 表示的是量纲统一后的地质变量；${\stackrel{-}{r}}_j$表示的是地质变量平均值；σ_j表示的是地质变量标准差。

以式（8）输出结果地质变量r'_j 为基础，采用二态赋值原则对地质变量 r'_j 进行赋值，简化深部资源预测的程序，提升深部资源预测的效率。地质变量赋值规则如下式所示：

为了提升计算的针对性，只依据式（9）的赋值规则，设置两种规则所对应的赋值结果。若地质变量在统计单元上无反应则将地质变量赋值为 0，若地质变量在统计单元上有反应，则将地质变量赋值为1，能够清晰地反映变量与成矿作用之间的信息，方便后续运算的应用与处理。

2.3 实验结果分析

以上述选取的实验对象与处理的地质变量为基础，进行矿床蚀变带深部资源预测实验。基于图1 流程中收集的矿床地层深部地质信息资料，并结合地质三维建模软件与计算机技术，以图2 的地质结构分布为参考，根据图5 所示的矿床结构以及各分区矿体、矿带分布情况，应用提出方法获得矿床蚀变带深部地质三维模型如图6所示。

如图6 所示，提出方法获得的地质三维模型可以清晰显示矿产资源的分布情况，为深部资源预测提供依据。为了直观显示提出方法的应用性能，选取甘肃寨上金矿南矿带构造叠加晕实用模型及深部找矿预测（王斌等，2021）与个旧老厂 Sn-Cu 矿床内外接触带矿体原生晕分带与深部矿体预测模型 （朱旭等，2021）作为对比方法，以实验对象实际深部资源开采数据为标准，计算深部资源预测误差，表达式为：

式（10）中，K表示的是深部资源预测误差数值； H^∗ 表示的是实际深部资源开采数值。

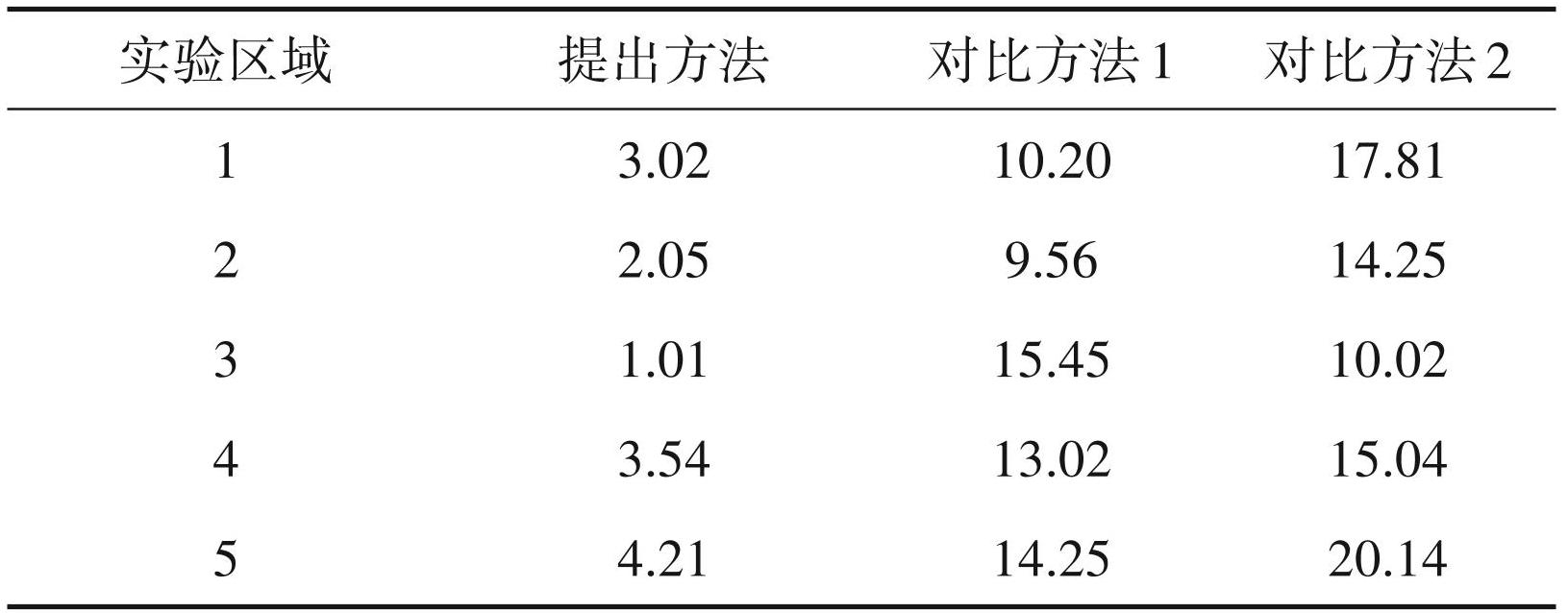
应用ArcGIS、MapGIS等地学软件处理收集矿床地层深部地质信息资料的内容，对实验对象的矿带分布、矿体平均品位进行分析。以表2 矿床主要组成元素的边界品位、最低工业品位、工业米百分值、可采厚度、夹石剔除厚度的指标为矿床蚀变带深部实际资源量的数据来源，按照指标在矿床随机选取 5个规模大小不同的区域作为实验对象。以图6矿床蚀变带深部地质三维模型为深部资源预测的数据来源，结合式（10）以实验对象实际深部资源开采数据为标准，计算深部资源预测误差。通过实验获得矿床蚀变带深部资源预测误差如表3所示。

结合图5和表2可知，矿床规模越大，其储量也就越大。在起伏地带，矿床铜元素的边界品位为 0.2×10^-2，工业米百分值为0.4 t，因此矿床各分区实际资源量均较大。如表3 数据所示，应用对比方法 1、对比方法 2 获得的资源预测误差最大值分别为 15.45%、20.14%，误差值偏大。而应用提出方法获得的矿床蚀变带深部资源预测误差最小值为 1. 01%，最大值仅为 4.21%。相较于 2 种对比方法来看，应用提出方法获得的矿床蚀变带深部资源预测误差数值较小，矿床深部资源量的预测与实际资源量较贴合，充分证实提出方法深部资源预测精度更高，具有良好的矿床深部资源量预测效果。

3 结束语

矿产资源开发与利用是保障社会经济发展的根本。随着浅表矿产资源的减少，深部资源勘查成为研究的重点。二维深部资源信息无法精准地预测深部资源的多少，故提出基于地质三维建模的矿床蚀变带深部资源预测方法研究。通过实验数据显示，提出方法有效降低了矿床蚀变带深部资源预测误差，为矿床开采计划的制定提供有力的依据与支撑。

参考文献