引 en

引用本文: 程小伟，贾书尧，鲍伟. 2024. 基于TWF评价法的煤矿冲击危险性评价［J］. 矿产勘查，15（6）：1032-1040.

Citation: Cheng Xiaowei，Jia Shuyao，Bao Wei. 2024. Evaluation of impact risk in underground mine based on TWF evaluation method［J］. Mineral Exploration， 15（6）：1032-1040.

基于TWF评价法的煤矿冲击危险性评价

程小伟¹

机构：

1. 河南龙宇能源股份有限公司陈四楼煤矿，河南永城 476600

×
，贾书尧^2,3,4

机构：

2. 中核能源科技有限公司，北京 100089
3. 中国矿业大学（北京）煤炭资源与安全开采国家重点实验室，北京 100083
4. 中国矿业大学（北京）力学与建筑工程学院，北京 100083

×
，鲍伟⁴

机构：

4. 中国矿业大学（北京）力学与建筑工程学院，北京 100083

×

1. 河南龙宇能源股份有限公司陈四楼煤矿，河南永城 476600；
2. 中核能源科技有限公司，北京 100089；
3. 中国矿业大学（北京）煤炭资源与安全开采国家重点实验室，北京 100083；
4. 中国矿业大学（北京）力学与建筑工程学院，北京 100083；

Evaluation of impact risk in underground mine based on TWF evaluation method

CHENG Xiaowei¹

Affiliation：

1. Chensilou Coal Mine， Henan Longyu Energy Co. ， Ltd. ， Yongcheng 476600 ， Henan， China

×
，JIA Shuyao^2,3,4

Affiliation：

2. Chinergy Co. ， Ltd， Beijing 100089 ， China
3. State Key Laboratory of Coal Resources and Safe Mining， China University of Mining and Technology（Beijing）， Beijing 100083 ， China
4. School of Mechanics and Civil Engineering， China University of Mining and Technology（Beijing）， Beijing 100083 ， China

×
，BAO Wei⁴

Affiliation：

4. School of Mechanics and Civil Engineering， China University of Mining and Technology（Beijing）， Beijing 100083 ， China

×

1. Chensilou Coal Mine， Henan Longyu Energy Co. ， Ltd. ， Yongcheng 476600 ， Henan， China；
2. Chinergy Co. ， Ltd， Beijing 100089 ， China；
3. State Key Laboratory of Coal Resources and Safe Mining， China University of Mining and Technology（Beijing）， Beijing 100083 ， China；
4. School of Mechanics and Civil Engineering， China University of Mining and Technology（Beijing）， Beijing 100083 ， China；

作者简介:

程小伟，男，1985年生，工程师，现从事煤矿安全生产工作；E-mail：chengxiaowei0601@126.com。

中图分类号:TD324

文献标识码:A

文章编号:1674-7801(2024)06-1032-09

DOI:10.20008/j.kckc.202406013

全文
图表
评论
参考文献
相似文献
出版信息

参考文献

白东东，冀兆，李鹏，廖泽. 2020. 半孤岛工作面冲击危险综合指数法评价与防治技术［J］. 煤炭科学技术， 48（S2）： 188‒193.

查找原文

参考文献

崔涛. 2019. 乘势而上推动煤炭工业高质量发展［J］. 煤炭经济研究， 39（3）： 1.

查找原文

参考文献

丁湘，闫鑫，李哲，浦治国，黄海鱼，刘溪，纪卓辰，张寅. 2023. 基于沉积控压规律的鄂尔多斯盆地中深部矿井冲击危险性分区评价［J］. 采矿与岩层控制工程学报， 5（4）： 44‒53.

查找原文

参考文献

胡大江. 2002. 煤岩损伤特性及冲击地压的研究［D］. 重庆：重庆大学.

查找原文

参考文献

蓝航，杜涛涛，彭永伟，张传玖，秦子晗. 2012. 浅埋深回采工作面冲击地压发生机理及防治［J］. 煤炭学报， 37（10）： 1618‒1623.

查找原文

参考文献

雷毅. 2005. 冲击危险性评价模型的建立及应用研究［D］. 北京：煤炭科学研究总院.

查找原文

参考文献

刘玉海. 2016. MapReduc大数据分析在煤矿的应用研究［J］. 软件， 37（5）： 101‒104.

查找原文

参考文献

刘占春，陈理强，王桂洋. 2013. 赵各庄矿3137工作面冲击危险性评价研究［J］. 科技资讯， 19： 54， 56.

查找原文

参考文献

潘俊锋，宁宇，毛德兵，蓝航，杜涛涛，彭永伟. 2012. 煤矿开采冲击地压启动理论［J］. 岩石力学与工程学报， 31（3）： 586‒596.

查找原文

参考文献

潘俊锋. 2019. 煤矿冲击地压启动理论及其成套技术体系研究［J］. 煤炭学报， 44（1）： 173‒182.

查找原文

参考文献

齐庆新，窦林名. 2008. 冲击矿压理论与技术［M］. 徐州：中国矿业大学出版社.

查找原文

参考文献

齐庆新，李一哲，赵善坤，张宁博，郑伟钰，李海涛，李宏艳. 2019. 我国煤矿冲击地压发展70年：理论与技术体系的建立与思考［J］. 煤炭科学技术， 47（9）： 1‒40.

查找原文

参考文献

乔懿麟，王苏健，学明，郝亚锋，李亮. 2016. 基于模糊综合评价的冲击矿压危险性信息平台研究［J］. 煤炭技术， 35（11）： 253‒255.

查找原文

参考文献

宋来智，王同旭，何勇，刘文杰，房武彬. 2015. 基于可能性指数诊断法的半孤岛工作面冲击危险性评价［J］. 煤矿安全， 46（8）： 209‒211.

查找原文

参考文献

王崇革，方洲，金云灿，孙悦. 2020. 基于融合赋权-云模型的煤矿冲击地压危险性评价［J］. 中国矿业， 29（6）： 97‒103.

查找原文

参考文献

王连国，孙求知，张连勇. 2000. 数量化理论在综采工作面安全评价中的应用［J］. 山东科技大学学报（自然科学版）， 19（4）： 73‒78.

查找原文

参考文献

魏振全. 2016. 残采煤柱工作面冲击地压危险性分析与防治技术［J］. 煤炭科学技术， 44（12）： 28‒32.

查找原文

参考文献

吴向前. 2010. 不稳定厚煤层一次采全高冲击危险性评价与防治［J］. 煤炭科学技术， 38（3）： 22‒27.

查找原文

参考文献

谢鹏飞. 2012. 济二矿上层煤采动影响下冲击地压预测与防治技术研究［D］. 辽宁：辽宁工程技术大学.

查找原文

参考文献

徐隽松，潘鹏志，陈建强，赵善坤，吴振华，刘旭东. 2022. 基于地应力反演的褶曲区煤层冲击危险性评价研究［J］. 煤炭科学技术， 51（9）： 35‒45.

查找原文

参考文献

张科学，亢磊，何满潮，刘金海，程志恒，孙健东，李东，赵启峰，殷帅峰，上官锋，王晓玲. 2020. 矿井煤层冲击危险性多层次综合评价研究［J］. 煤炭科学技术， 48（8）： 82‒89.

查找原文

参考文献

张宁博，赵善坤，邓志刚，李海涛，王寅，秦凯. 2019. 动静载作用下逆冲断层力学失稳机制研究［J］. 采矿与安全工程学报， 36（6）： 1186‒1192.

查找原文

参考文献

周光亚，董文泉，夏立显. 1979. 关于数量化理论Ⅰ、Ⅱ的数学模型［J］. 吉林大学自然科学学报，（1）： 11‒18.

查找原文

目录contents

摘要 Abstract
关键词 Keywords
0 引言
1 TWF 冲击地压危险性评价方法
1.1 评价指标的选取
1.2 TWF评价方法计算评价指标权重
1.3 危险性指数判据及等级划分
2 工程实例
3 TWF 冲击危险性综合评价系统
3.1 TWF评价系统开发
3.2 评价系统输入模块
3.3 评价系统分析模块
4 结论
参考文献

摘要

冲击地压作为煤矿生产过程中常见的动力灾害，给煤矿安全生产带来极大威胁，因此，工作面回采前进行冲击危险性评价尤为重要。为构建冲击地压危险性的科学评价模型，本文收集和研究了140个煤矿工作面实例，分析了冲击地压的影响因素，从每个案例中提取14项评价指标，并建立了数据库。基于数量化理论评价法与模糊评价法，建立了适用性更强的TWF（theory of quantification with fuzzy evaluation）评价法，该方法继承了数量化理论和模糊评价法的优势，并将煤矿冲击危险程度划分为5个等级。以河南某煤矿工作面为背景，采用 TWF 冲击危险性评价模型对该工作面进行了冲击危险性评价，得出危险性指数为 19. 83，评价结果为无冲击危险性，与现场实际相符，表明该评价模型具有较强的适用性；开发了TWF综合评价系统，持续的案例补充可不断提高TWF评价模型的评价精度，研究成果可为冲击地压危险评价提供一定的理论参考。

Abstract

Rock burst is a common dynamic disaster in the process of coal mine production. It poses a great threat to coal mine safety production. Therefore， it is particularly important to evaluate the impact risk before the mining of the working face. To construct the evaluation model of rock burst risk， this paper collected and studied 140 examples of coal mine working faces. The influencing factors of rock burst were analyzed，14 evaluation indexes were extracted from each case， and a database was established. Based on the quantitative theory evaluation method and fuzzy evaluation method， the theory of quantification with fuzzy evaluation was established. This method inherited the advantages of the two and divided the risk degree of coal mine impact into five grades. The TWF impact risk assessment model was used to evaluate the impact risk of a coal mine working face in Henan Province. The risk index is 19. 83， and the evaluation result is no impact risk. It shows that the evaluation model has strong applicability. The TWF comprehensive evaluation system is developed， and the continuous case supplement can continuously improve the evaluation accuracy of the TWF evaluation model. The research results can provide a theoretical reference for the risk assessment of rock bursts.

关键词

冲击危险性评价；模糊评价；数量化理论； TWF评价方法； TWF综合评价系统

Keywords

rock burst risk assessment ； fuzzy evaluation method ； theory of quantitative ； TWF evaluation method ； TWF comprehensive evaluation system

0 引言
随着矿产资源的短缺，中国多数矿山由露天开采转为地下开采，开采深度不断增加（齐庆新等， 2019）。与此同时，深部开采所引发的各种灾害问题层出不穷，其中，以冲击地压动力灾害最为突出（崔涛，2019）。冲击地压是工作面围岩弹性能瞬间释放造成围岩及支护结构剧烈破坏的现象（蓝航等，2012；潘俊锋等，2012；潘俊锋，2019），具有破坏形式多样、灾害突发性强和破坏巨大等特点。为保证煤矿安全开采，建立科学的冲击地压危险性评价方法尤为必要。
传统评价方法包括层次分析法（乔懿麟等 2016；张宁博等，2019；张科学等，2020）、综合指数法（齐庆新和窦林名，2008；魏振全，2016；白东东等，2020；徐隽松等，2022）、可能性指数法（宋来智等，2015）、经验类比法（胡大江，2002；谢鹏飞， 2012）等，这些方法存在考虑影响因素较少、主观判断占比大等问题。随着数学等基础学科理论在工程实际的广泛应用，更多计算方法被引入到冲击危险评价模型的构建中。刘玉海（2016）基于大数据云计算 MapReduce 搭建概念框架处理数据，对矿井大数据进行了进一步的大规模整合，实现了可拓展化，准确预测了开采矿井的冲击地压危险程度；王连国等（2000）、吴向前（2010）应用数量化理论把冲击危险影响因素的定性指标转换为数量指标表达；王崇革等（2020）将 AHP 分析法与 CRITIC 赋权法结合，实现了主客观的对立统一；丁湘等（2023）将灰色关联度法和层次分析法结合，确定了各因素的权重值，基于 ArcGIS 平台上建立了各主控因素专题图，构建了冲击危险性评价模型。
针对冲击危险性评价，目前已经取得了大量的成果。但是冲击地压的影响因素众多，诱导原因复杂，如何结合采掘过程中的相关数据得到更加符合实际的评价结果是需要进一步解决的问题。基于此，本文以现有的观测数据和大量煤矿工作面案例数据为基础，应用数学建模工具对矿井数据资料进行大规模整合，分析冲击地压灾害的诱导因素，形成完善的评价体系，建立TWF评价方法并开发TWF 评价程序，同时对其准确性进行了验证，以期能为煤矿冲击地压灾害综合管控提供一定参考。
1 TWF 冲击地压危险性评价方法
TWF 评价法（Theory of quantification with Fuzzy evaluation）将数量化理论与模糊评价方法相结合，继承了数量化理论评价法和模糊评价法的优势，互补了两种评价方法的缺陷。本文综合分析影响冲击地压的定量指标与定性指标，以期在表明冲击地压影响因素的说明变量和表明冲击地压状态的基准变量之间搭建桥梁，其流程如图1所示。
图1 TWF评价方法流程
1.1 评价指标的选取
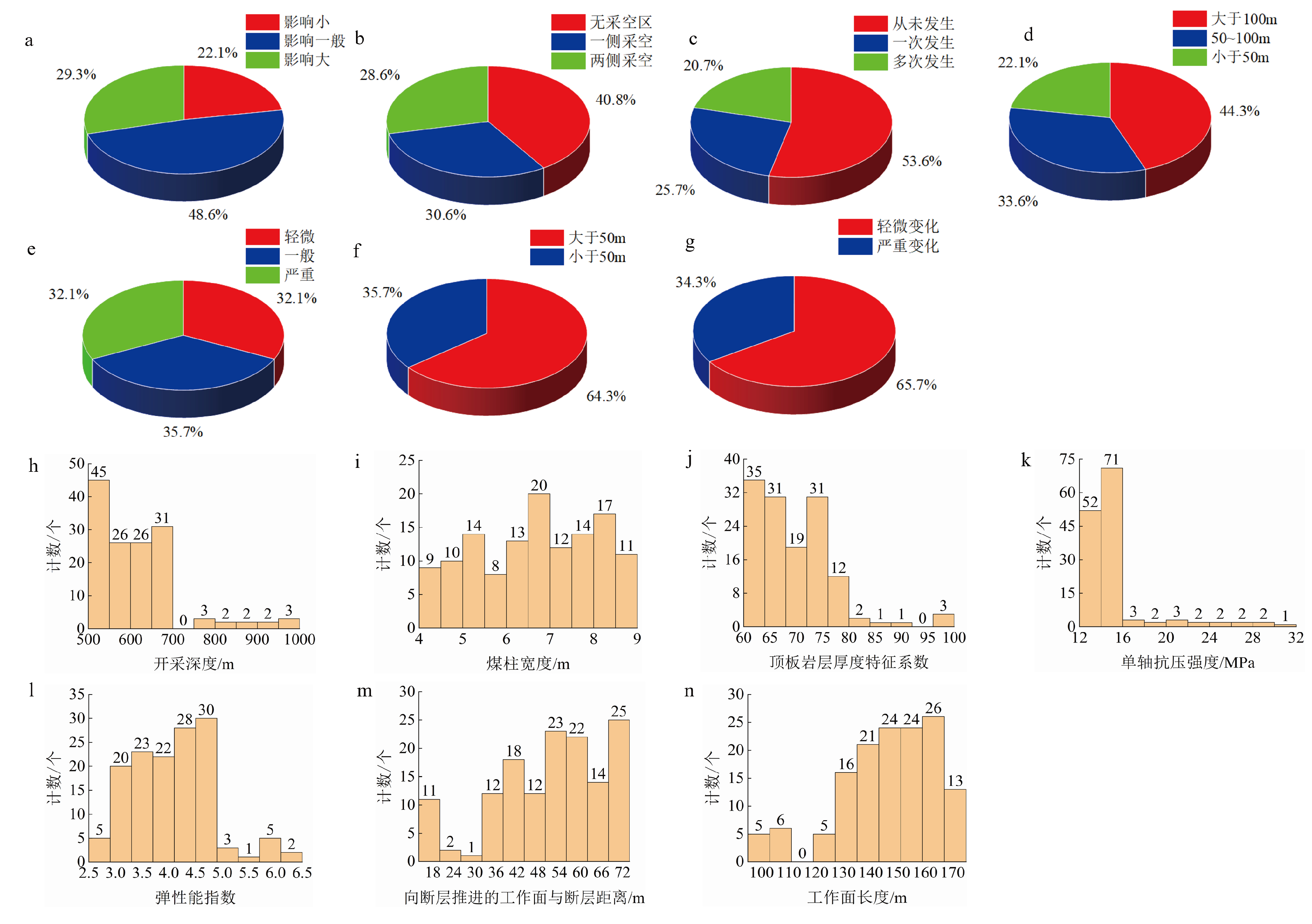
本文共收集了 140 个煤矿项目数据，从每个案例中提取 14 项评价指标，建立案例数据库，为 TWF 评价法奠定基础。这些评价指标包含定性指标和定量指标（表1），其中各个指标数据特征如图2 所示。
图2 各指标数据特征
a—巷道交叉处影响饼状图；b—临近采空区关系饼状图；c—发生过冲击地压次数的饼状图；d—倾斜煤层与工作面距离的饼状图；e—褶皱程度饼状图；f—坚硬厚岩层距煤层距离饼状图；g—煤层厚度变化饼状图；h—开采深度直方图；i—煤柱宽度直方图；j—顶板岩层厚度特征系数直方图；k—煤单轴抗压强度直方图；l—煤弹性能指数直方图；m—工作面与断层距离直方图；n—工作面长度直方图
表1 冲击地压评价指标
1.2 TWF评价方法计算评价指标权重
（1）确定模糊集合
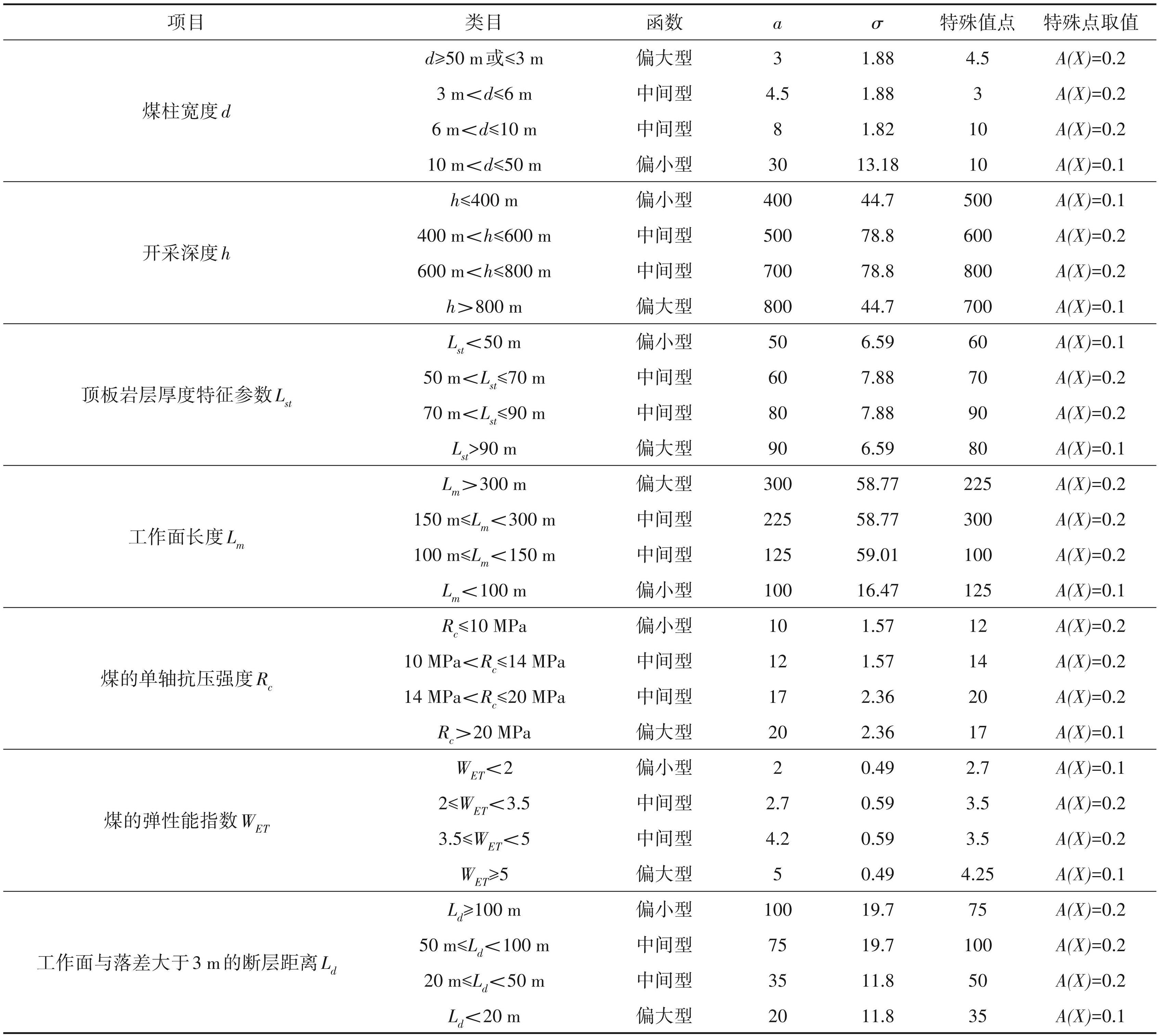
在冲击地压评价中，模糊集合主要用于确定评价指标中的定量指标，根据评价指标的具体分级，涉及的评价指标和等级划分情况如表2所示。把各项目的 4 个类目分别定为Ⅰ级，Ⅱ级，Ⅲ级，Ⅳ级。等级越高则说明对安全生产越不利，越容易引发冲击地压灾害。然后根据各类目数据形态，确定每种类目的隶属函数。
（2）计算隶属度
TWF评价方法使用指派法隶属函数确定方法。根据其特征和相关属性，使用正态分布型（中间型）隶属函数。
表2 定量评价指标等级划分
中间型隶属度计算公式为：

A (X) = e x p [- {(\frac{x - a}{σ})}^{2}]

(1)

式（1）中：A为某一项目下某一类目的隶属度；X 为影响因素；a为端点横坐标；σ为方差。
根据相应等级的结构和特殊点取值来确定各个公式的a与σ的值，结果如表3所示。
（3）TWF法计算权重
TWF 评价方法中使用数量化理论（周光亚等， 1979；王连国等，2000），将定性指标与定量指标放在同一维度下进行整合。为了使数量化理论更加契合冲击地压危险性评价，需要对其计算过程进行部分优化。
若问题涉及m个项目x₁，x₂，···， x_m，第l个项目为 x_l。这些项目组成的向量 X为说明变量。同时涉及评价的参考案例有n个。设第一个项目x₁的类目共有r₁个，分别为C₁₁，C₁₂，C₁₃，···，C_1r1，第j个项目x_j 的类目共有r_j个，分别为C_i1，C_i₂，C_i3，···，C_irj。
设δ_jk（i）为第j个定性项目k子类目在第i个样品中的反应。其中 j、k、i 的取值范围分别为：j=1，2， 3，···，m；k=1，2，3，···，r_j；i=1，2，3，···， n。当第 i 个样品在第 j 个项目的反应为 k 类目时，δ_jk（i）= 1，所以得：

\sum_{k = 1}^{r_{j}} δ_{j k} (i) = 1

(2)

设 ${\bar{δ}}_{j x} （ i ）$ 为第 i个样品中，第 j个定量项目的 x子类目的反应，称之为修正后的反应。对其进行归一化，公式为：

{\bar{δ}}_{j x} (i) = \frac{A_{i} (x)}{\sum_{i = 1}^{4} A_{i} (x)}, x = 1,2, 3,4

(3)

当每个 $δ_{j ， k} （ i ）$ ， ${\bar{δ}}_{j x} （ i ）$ 计算完成后，将其进行组合构成m×n阶矩阵，并称之为反应矩阵：

X = [\begin{matrix} δ_{11} (1) & \cdot \cdot \cdot & δ_{l 1} (1) & \cdot \cdot \cdot & {\bar{δ}}_{m r_{m}} (1) \\ \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot \\ δ_{11} (i) & \cdot \cdot \cdot & δ_{l 1} (i) & \cdot \cdot \cdot & {\bar{δ}}_{m r_{m}} (i) \\ \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot \\ δ_{11} (n) & \cdot \cdot \cdot & δ_{l 1} (n) & \cdot \cdot \cdot & {\bar{δ}}_{m r_{m}} (n) \end{matrix}]

(4)

总类目个数P为：

P = \sum_{j = 1}^{m} r_{j}

(5)

在冲击地压危险评价方法中，每个参考案例的最终评价指数为 y₁，y₂，···， y_n，y为各个样本的基准变量测定值，第 i 个样本基准变量为 y_i，这些指数组成的向量Y为基准变量，则：

y_{i} = \sum_{j = 1}^{m} \sum_{k = 1}^{r_{j}} δ_{j k} (i) a_{j k} + ε_{i}

(6)

式（6）中：a_jk表示第 j 个项目的第 k 类目对基准变量的影响系数。ε_i是第i个抽样样本的随机误差。根据最小二乘法来寻求系数 a_jk的估计量，则误差量为最小值时的方程（周光亚等，1979）为：

\sum_{i = 1}^{n} ε_{i}^{2} = \sum_{i = 1}^{n} {[y_{i} - \sum_{j = 1}^{m} \sum_{k = 1}^{r_{j}} δ_{j k} (i) a_{j k}]}^{2}

(7)

当误差量达到最小值时，记 a_jk为 ${\hat{a}}_{j k}$ ，修正后系数向量集合为 A。设 uv 的范围满足：u=1，2，···m；v=1，2，···r_j。则可以求得偏导数函数为：
表3 各类目隶属函数

\sum_{i = 1}^{n} δ_{u v} (i) y_{i} = \sum_{j = 1}^{m} \sum_{k = 1}^{r_{j}} [\sum_{i = 1}^{n} δ_{j k} (i) δ_{u v} (i)] {\hat{a}}_{j k}

(8)

如果用矩阵来表示，令系数向量：

A = [a_{j k}] = {[a_{11}, a_{12}, a_{13} \cdot \cdot \cdot a_{m r_{n}}]}^{T}

(9)

误差向量：

E = [ε_{i}] = {[ε_{1}, ε_{2}, \cdot \cdot \cdot, ε_{n}]}^{T}

(10)

基准向量：

Y = [y_{i}] = {[y_{1}, y_{2}, \cdot \cdot \cdot y_{n}]}^{T}

(11)

则原线性公式可以写成：

Y = X A + E

(12)

在正规方程组的建立中，需要对反应矩阵进行删减来保证矩阵满秩，进一步得到的向量方程为：

X^{T} X \hat{a} = X^{T} Y

(13)

其中 $\hat{a} = {[{\hat{a}}_{11} ， \cdot \cdot \cdot {\hat{a}}_{21} ， \cdot \cdot \cdot {\hat{a}}_{2 r_{2}} ， \cdot \cdot \cdot {\hat{a}}_{m 1} ， \cdot \cdot \cdot ， {\hat{a}}_{m r_{m}}]}^{T}$ 。这里求得的 $\hat{a}$ 就是各项目类目权重。
（4）计算衡量精度
对于系数矩阵 $\hat{a}$ ，需要研究其与原数据的相符程度，由于数量化理论与回归分析一脉相承，可以把回归分析中的复相关系数理论和剩余均方差引用过来衡量其精准度，确保评价结果收敛。
这里设 $\hat{y}$ 为使用修正后系数向量 $\hat{a}$ 所计算得出的基准变量。 $\bar{y}$ 为基准变量均值。通过复相关系数 r 来衡量修正前后基准变量的相关性，其对应公式为（周光亚等，1979）：

r = \frac{σ_{\hat{y}}}{σ_{y}} = \sqrt{\frac{\sum_{i = 1}^{n} {({\hat{y}}_{i} - \bar{y})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}

(14)

剩余均方差β（周光亚等，1979）为：

β = \sum_{i = 1}^{n} {({\hat{y}}_{i} - \bar{y})}^{2}

(15)

r 值较大和 β 值较小时，预测精度较高，反之则较低。根据计算可得，TWF评价方法中r=0.879；β= 0.313，说明该评价方法拟合较好，精度较高。
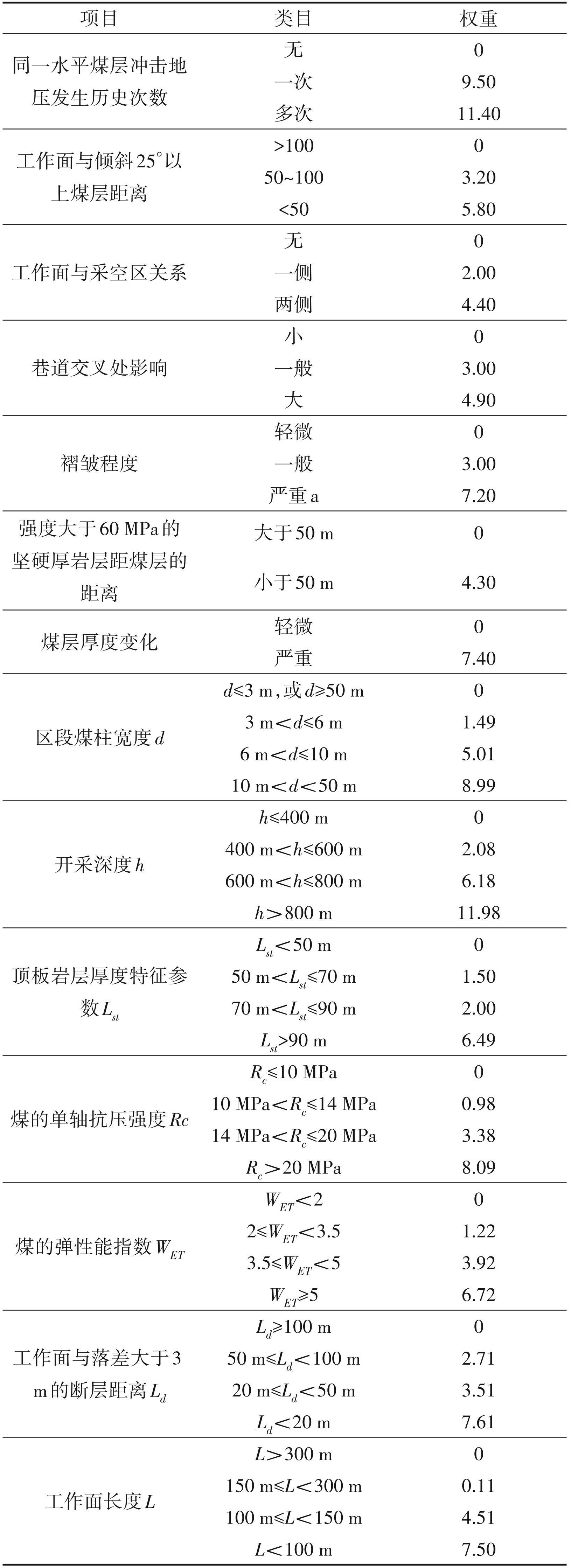
根据TWF评价方法计算，最终得到的各评价指标的权重值，具体见表4。
1.3 危险性指数判据及等级划分
将定量数据带入模糊函数中，求出各项目类目隶属度。将定性数据各项目类目和定量数据各项目类目隶属度乘以相应的权重值，得到最终冲击危险性指数Y，其公式为：

Y = \sum_{k = 1}^{r_{1}} {\hat{a}}_{1 k} w_{1 k} + \sum_{k = 1}^{r_{2}} {\hat{a}}_{2 k} w_{2 k} + \cdot \cdot \cdot + \sum_{k = 1}^{r_{m}} {\hat{a}}_{m k} w_{m k}

(16)

如表5 所示，根据各矿井工作面的冲击地压响应结果和冲击地压危险状态评价标准，判断出各煤矿案例的冲击危险性指数及冲击危险等级。
2 工程实例
本文以河南某煤矿为工程背景验证评价方法可行性，共选取 14个评价指标（表6）。分别选取综合指数法、可能性指数法、TWF 评价法进行分析评价（表7）。根据综合指数法（雷毅，2005）可知该工作面无冲击危险性。根据可能性指数法（雷毅，2005）可知该工作面为大概率发生冲击地压。根据 TWF 评价法求得该工作面无冲击危险性。由河南某煤矿工作面实际回采情况可知，该工作面并无冲击地压事故发生，冲击危险性较小，验证了 TWF 冲击危险性评价方法的准确性，其结果对比如表7所示。
3 TWF 冲击危险性综合评价系统
3.1 TWF评价系统开发
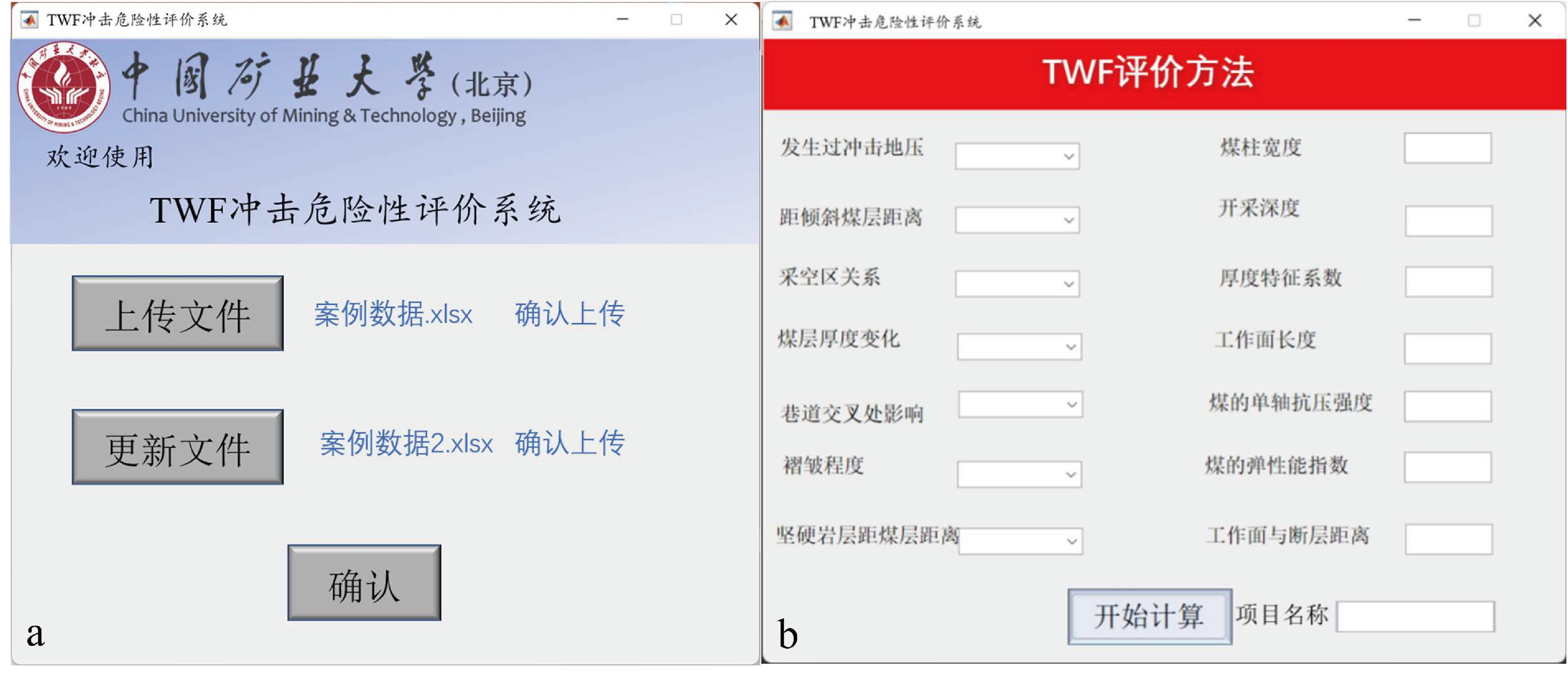
TWF 冲击地压危险性综合评价系统由 GUI 程序进行编制，其包括两大模块，分别为输入模块和分析模块。输入模块包括“案例输入”和“参数输入”两个功能；分析模块包括“案例统计”和“危险性分析”两个功能。TWF冲击地压危险性评价系统界面如图3a所示。
表4 各评价指标权重值
表5 冲击地压危险状态评价标准
表6 工作面影响因素的冲击地压评价
表7 河南某煤矿冲击地压评价结果对比
3.2 评价系统输入模块
TWF 评价系统中输入模块的“案例输入”主要作用是实时导入案例数据，不断发展数据库规模，可为评价系统的持续优化提供支撑。
当需要对某一具体煤矿工作面进行冲击危险性评价时，就在 TWF 评价系统中输入模块的“参数输入”功能，进入界面如图3b所示。
3.3 评价系统分析模块
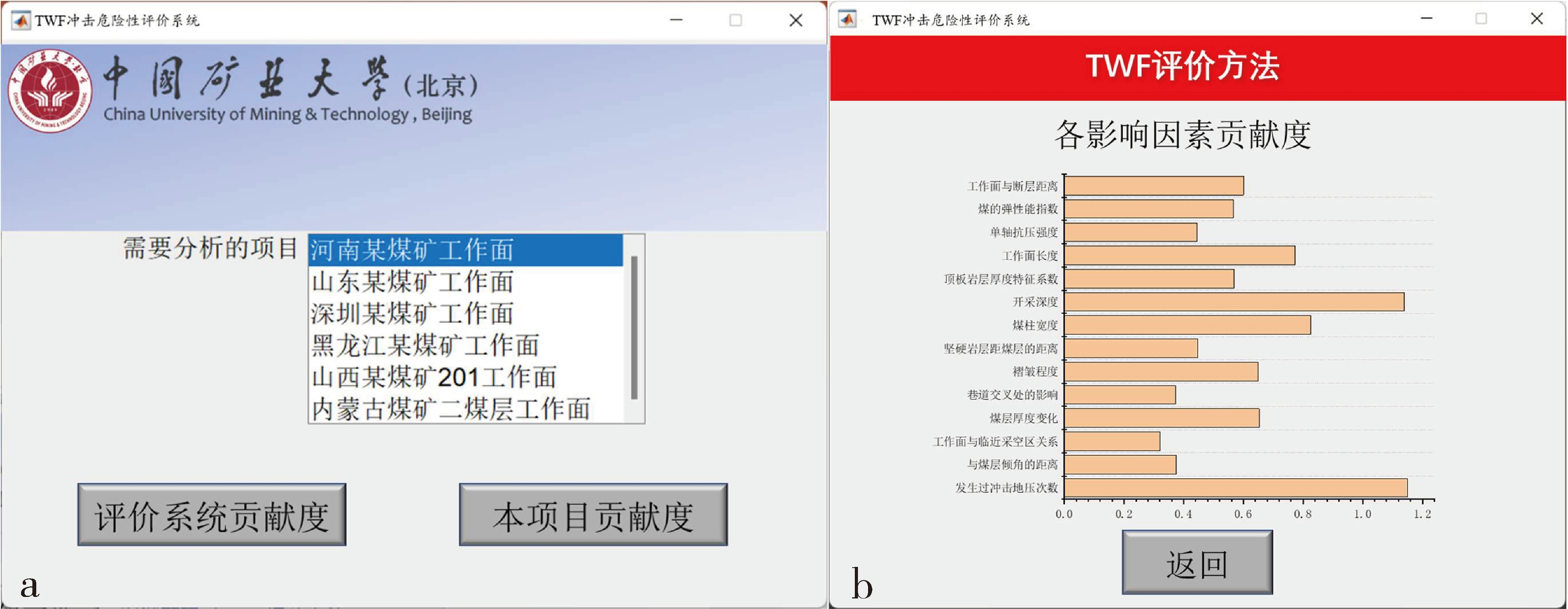
本文使用3种参数分析贡献度，即偏相关系数、方差比和量程。偏相关系数可以有效反映影响权重大小，其与相关性成正比。方差比高说明两组数据同频同步，说明该项目与基准变量关联度高，则其影响程度越高。使用各项目的量程，也就是范围可以衡量贡献度大小。
通过图4a中“危险性分析”模块可查看图4b所示的各影响因素贡献度。“评价系统贡献度”可以计算得到 TWF 综合评价系统中各评价因素对冲击地压危险性的贡献度；“本项目贡献度”模块可以对该煤矿工作面的冲击地压各影响因素危险程度大小做出判断。
图3 系统主界面（a）及参数输入界面（b）
图4 危险性分析模块界面（a）及各影响因素贡献度界面（b）
4 结论
（1）本文收集了140个煤矿项目数据，从每个案例中提取了包含定性指标和定量指标在内的 14 项评价指标，为评价模型的建立奠定基础。
（2）基于数量化理论和模糊评价方法，建立了适用性更强的评价方法，即TWF评价方法。通过分析河南某煤矿案例，结合煤矿工作面实际回采情况可知，TWF冲击危险性评价方法评价精度较高。且评价结果与工作面实际情况一致，为煤矿冲击危险性评判提供了一种高精准、低成本的新方法。
（3）编制了 TWF 冲击地压危险性综合评价系统，可同时完成数量化理论的权重计算、模糊评价法的参数处理和TWF评价方法的数据分析，最终求得冲击地压危险性等级和各影响因素的贡献度。
参考文献
- 白东东，冀兆，李鹏，廖泽. 2020. 半孤岛工作面冲击危险综合指数法评价与防治技术［J］. 煤炭科学技术， 48（S2）： 188‒193.
- 崔涛. 2019. 乘势而上推动煤炭工业高质量发展［J］. 煤炭经济研究， 39（3）： 1.
- 丁湘，闫鑫，李哲，浦治国，黄海鱼，刘溪，纪卓辰，张寅. 2023. 基于沉积控压规律的鄂尔多斯盆地中深部矿井冲击危险性分区评价［J］. 采矿与岩层控制工程学报， 5（4）： 44‒53.
- 胡大江. 2002. 煤岩损伤特性及冲击地压的研究［D］. 重庆：重庆大学.
- 蓝航，杜涛涛，彭永伟，张传玖，秦子晗. 2012. 浅埋深回采工作面冲击地压发生机理及防治［J］. 煤炭学报， 37（10）： 1618‒1623.
- 雷毅. 2005. 冲击危险性评价模型的建立及应用研究［D］. 北京：煤炭科学研究总院.
- 刘玉海. 2016. MapReduc大数据分析在煤矿的应用研究［J］. 软件， 37（5）： 101‒104.
- 刘占春，陈理强，王桂洋. 2013. 赵各庄矿3137工作面冲击危险性评价研究［J］. 科技资讯， 19： 54， 56.
- 潘俊锋，宁宇，毛德兵，蓝航，杜涛涛，彭永伟. 2012. 煤矿开采冲击地压启动理论［J］. 岩石力学与工程学报， 31（3）： 586‒596.
- 潘俊锋. 2019. 煤矿冲击地压启动理论及其成套技术体系研究［J］. 煤炭学报， 44（1）： 173‒182.
- 齐庆新，窦林名. 2008. 冲击矿压理论与技术［M］. 徐州：中国矿业大学出版社.
- 齐庆新，李一哲，赵善坤，张宁博，郑伟钰，李海涛，李宏艳. 2019. 我国煤矿冲击地压发展70年：理论与技术体系的建立与思考［J］. 煤炭科学技术， 47（9）： 1‒40.
- 乔懿麟，王苏健，学明，郝亚锋，李亮. 2016. 基于模糊综合评价的冲击矿压危险性信息平台研究［J］. 煤炭技术， 35（11）： 253‒255.
- 宋来智，王同旭，何勇，刘文杰，房武彬. 2015. 基于可能性指数诊断法的半孤岛工作面冲击危险性评价［J］. 煤矿安全， 46（8）： 209‒211.
- 王崇革，方洲，金云灿，孙悦. 2020. 基于融合赋权-云模型的煤矿冲击地压危险性评价［J］. 中国矿业， 29（6）： 97‒103.
- 王连国，孙求知，张连勇. 2000. 数量化理论在综采工作面安全评价中的应用［J］. 山东科技大学学报（自然科学版）， 19（4）： 73‒78.
- 魏振全. 2016. 残采煤柱工作面冲击地压危险性分析与防治技术［J］. 煤炭科学技术， 44（12）： 28‒32.
- 吴向前. 2010. 不稳定厚煤层一次采全高冲击危险性评价与防治［J］. 煤炭科学技术， 38（3）： 22‒27.
- 谢鹏飞. 2012. 济二矿上层煤采动影响下冲击地压预测与防治技术研究［D］. 辽宁：辽宁工程技术大学.
- 徐隽松，潘鹏志，陈建强，赵善坤，吴振华，刘旭东. 2022. 基于地应力反演的褶曲区煤层冲击危险性评价研究［J］. 煤炭科学技术， 51（9）： 35‒45.
- 张科学，亢磊，何满潮，刘金海，程志恒，孙健东，李东，赵启峰，殷帅峰，上官锋，王晓玲. 2020. 矿井煤层冲击危险性多层次综合评价研究［J］. 煤炭科学技术， 48（8）： 82‒89.
- 张宁博，赵善坤，邓志刚，李海涛，王寅，秦凯. 2019. 动静载作用下逆冲断层力学失稳机制研究［J］. 采矿与安全工程学报， 36（6）： 1186‒1192.
- 周光亚，董文泉，夏立显. 1979. 关于数量化理论Ⅰ、Ⅱ的数学模型［J］. 吉林大学自然科学学报，（1）： 11‒18.

图1 TWF评价方法流程

图2 各指标数据特征

图3 系统主界面（a）及参数输入界面（b）

图4 危险性分析模块界面（a）及各影响因素贡献度界面（b）

表1 冲击地压评价指标

表2 定量评价指标等级划分

表3 各类目隶属函数

表4 各评价指标权重值

表5 冲击地压危险状态评价标准

表6 工作面影响因素的冲击地压评价

表7 河南某煤矿冲击地压评价结果对比

相似文献

基本信息

中图分类号: TD324
文献标识码: A
DOI: 10.20008/j.kckc.202406013
文章编号: 1674-7801(2024)06-1032-09

基金信息

本文受中国矿业大学（北京）煤炭资源与安全开采国家重点实验室开放基金项目（SKLCRSM20KFA11）资助；

引用信息

程小伟，贾书尧，鲍伟. 2024. 基于TWF评价法的煤矿冲击危险性评价［J］. 矿产勘查，15（6）：1032-1040.

Cheng Xiaowei，Jia Shuyao，Bao Wei. 2024. Evaluation of impact risk in underground mine based on TWF evaluation method［J］. Mineral Exploration， 15（6）：1032-1040.

稿件历史

收稿日期: 2022-11-16

参考文献

白东东，冀兆，李鹏，廖泽. 2020. 半孤岛工作面冲击危险综合指数法评价与防治技术［J］. 煤炭科学技术， 48（S2）： 188‒193.
崔涛. 2019. 乘势而上推动煤炭工业高质量发展［J］. 煤炭经济研究， 39（3）： 1.
丁湘，闫鑫，李哲，浦治国，黄海鱼，刘溪，纪卓辰，张寅. 2023. 基于沉积控压规律的鄂尔多斯盆地中深部矿井冲击危险性分区评价［J］. 采矿与岩层控制工程学报， 5（4）： 44‒53.
胡大江. 2002. 煤岩损伤特性及冲击地压的研究［D］. 重庆：重庆大学.
蓝航，杜涛涛，彭永伟，张传玖，秦子晗. 2012. 浅埋深回采工作面冲击地压发生机理及防治［J］. 煤炭学报， 37（10）： 1618‒1623.
雷毅. 2005. 冲击危险性评价模型的建立及应用研究［D］. 北京：煤炭科学研究总院.
刘玉海. 2016. MapReduc大数据分析在煤矿的应用研究［J］. 软件， 37（5）： 101‒104.
刘占春，陈理强，王桂洋. 2013. 赵各庄矿3137工作面冲击危险性评价研究［J］. 科技资讯， 19： 54， 56.
潘俊锋，宁宇，毛德兵，蓝航，杜涛涛，彭永伟. 2012. 煤矿开采冲击地压启动理论［J］. 岩石力学与工程学报， 31（3）： 586‒596.
潘俊锋. 2019. 煤矿冲击地压启动理论及其成套技术体系研究［J］. 煤炭学报， 44（1）： 173‒182.
齐庆新，窦林名. 2008. 冲击矿压理论与技术［M］. 徐州：中国矿业大学出版社.
齐庆新，李一哲，赵善坤，张宁博，郑伟钰，李海涛，李宏艳. 2019. 我国煤矿冲击地压发展70年：理论与技术体系的建立与思考［J］. 煤炭科学技术， 47（9）： 1‒40.
乔懿麟，王苏健，学明，郝亚锋，李亮. 2016. 基于模糊综合评价的冲击矿压危险性信息平台研究［J］. 煤炭技术， 35（11）： 253‒255.
宋来智，王同旭，何勇，刘文杰，房武彬. 2015. 基于可能性指数诊断法的半孤岛工作面冲击危险性评价［J］. 煤矿安全， 46（8）： 209‒211.
王崇革，方洲，金云灿，孙悦. 2020. 基于融合赋权-云模型的煤矿冲击地压危险性评价［J］. 中国矿业， 29（6）： 97‒103.
王连国，孙求知，张连勇. 2000. 数量化理论在综采工作面安全评价中的应用［J］. 山东科技大学学报（自然科学版）， 19（4）： 73‒78.
魏振全. 2016. 残采煤柱工作面冲击地压危险性分析与防治技术［J］. 煤炭科学技术， 44（12）： 28‒32.
吴向前. 2010. 不稳定厚煤层一次采全高冲击危险性评价与防治［J］. 煤炭科学技术， 38（3）： 22‒27.
谢鹏飞. 2012. 济二矿上层煤采动影响下冲击地压预测与防治技术研究［D］. 辽宁：辽宁工程技术大学.
徐隽松，潘鹏志，陈建强，赵善坤，吴振华，刘旭东. 2022. 基于地应力反演的褶曲区煤层冲击危险性评价研究［J］. 煤炭科学技术， 51（9）： 35‒45.
张科学，亢磊，何满潮，刘金海，程志恒，孙健东，李东，赵启峰，殷帅峰，上官锋，王晓玲. 2020. 矿井煤层冲击危险性多层次综合评价研究［J］. 煤炭科学技术， 48（8）： 82‒89.
张宁博，赵善坤，邓志刚，李海涛，王寅，秦凯. 2019. 动静载作用下逆冲断层力学失稳机制研究［J］. 采矿与安全工程学报， 36（6）： 1186‒1192.
周光亚，董文泉，夏立显. 1979. 关于数量化理论Ⅰ、Ⅱ的数学模型［J］. 吉林大学自然科学学报，（1）： 11‒18.

分享给微信好友或者朋友圈

使用微信“扫一扫”功能。

基于TWF评价法的煤矿冲击危险性评价

Evaluation of impact risk in underground mine based on TWF evaluation method

摘要

Abstract

关键词

Keywords

0 引言

1 TWF 冲击地压危险性评价方法

1.1 评价指标的选取

1.2 TWF评价方法计算评价指标权重

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

1.3 危险性指数判据及等级划分

(16)

2 工程实例

3 TWF 冲击危险性综合评价系统

3.1 TWF评价系统开发

3.2 评价系统输入模块

3.3 评价系统分析模块

4 结论

参考文献

相似文献

基本信息

基金信息

引用信息

稿件历史

参考文献