引 en

引用本文: 卢许佳，杨润基，高庆，谭维佳. 2024. 适用于一般时变荷载情况的一维固结解析解［J］. 矿产勘查，15（6）：1084-1091.

Citation: Lu Xujia，Yang Runji，Gao Qing，Tan Weijia. 2024. One dimensional analytical solution of consolidation for general time-varying load cases［J］. Mineral Exploration，15（6）：1084-1091.

适用于一般时变荷载情况的一维固结解析解

卢许佳¹

机构：

1. 中国水利水电第七工程局有限公司，四川成都 611730

×
，杨润基¹

机构：

1. 中国水利水电第七工程局有限公司，四川成都 611730

×
，高庆²

机构：

2. 中铁三局集团有限公司，四川成都 611730

×
，谭维佳³

机构：

3. 长安大学地质工程与测绘学院，陕西西安 710054

×

1. 中国水利水电第七工程局有限公司，四川成都 611730；
2. 中铁三局集团有限公司，四川成都 611730；
3. 长安大学地质工程与测绘学院，陕西西安 710054；

One dimensional analytical solution of consolidation for general time-varying load cases

LU Xujia¹

Affiliation：

1. Sinohydro Bureau 7 Co. ， Ltd. ， Chengdu 611730 ， Sichuan， China

×
，YANG Runji¹

Affiliation：

1. Sinohydro Bureau 7 Co. ， Ltd. ， Chengdu 611730 ， Sichuan， China

×
，GAO Qing²

Affiliation：

2. China Railway Third Bureau Group Co. ， Ltd. ， Chengdu 611730 ， Sichuan， China

×
，TAN Weijia³

Affiliation：

3. School of Geological Engineering and Surveying and Mapping， Chang'an University， Xi'an 710054 ， Shaanxi， China

×

1. Sinohydro Bureau 7 Co. ， Ltd. ， Chengdu 611730 ， Sichuan， China；
2. China Railway Third Bureau Group Co. ， Ltd. ， Chengdu 611730 ， Sichuan， China；
3. School of Geological Engineering and Surveying and Mapping， Chang'an University， Xi'an 710054 ， Shaanxi， China；

作者简介:

卢许佳，男，1985年生，高级工程师，从事铁路施工管理工作；E-mail：117267308@qq.com。

通讯作者:

谭维佳，男，1988年生，博士，工程师，主要从事工程地质和地质灾害研究；E-mail：za254016@163.com。

中图分类号:TU431

文献标识码:A

文章编号:1674-7801(2024)06-1084-08

DOI:10.20008/j.kckc.202406019

全文
图表
评论
参考文献
相似文献
出版信息

参考文献

Baligh M M， Levadoux J N. 1978. Consolidation theory for cyclic loading［J］. Journal of the Geotechnical Engineering Division， 104（4）： 415‒431.

查找原文

参考文献

Biot M A. 1941. General theory of three-dimensional consolidation［J］. Journal of Applied Physics， 12（2）： 155‒164.

查找原文

参考文献

De Boer R. 2005. Trends in Continuum Mechanics of Porous Media［M］. Berlin： Springer Science & Business Media.

查找原文

参考文献

Favaretti M， Soranzo M. 1995. A simplified consolidation theory in cyclic loading conditions［C］//Compression and Consolidation of Clayey Soils， 405‒409. Netherlands： Balkema.

查找原文

参考文献

Geng X， Xu C， Cai Y. 2006. Non-linear consolidation analysis of soil with variable compressibility and permeability under cyclic loadings［J］. International Journal for Numerical & Analytical Methods in Geomechanics， 30（8）： 803‒821.

查找原文

参考文献

Logan J D. 2004. Applied Partial Differential Equations［M］. NewYork： Springer-Verlag.

查找原文

参考文献

Olson R E. 1977. Consolidation under time dependent loading［J］. Journal of the Geotechnical Engineering Division， 103（1）： 55‒60.

查找原文

参考文献

Razouki S S， Bonnier P， Datcheva M， Schanz T. 2013. Analytical solution for 1D consolidation under haversine cyclic loading［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 37（14）： 2367‒2372.

查找原文

参考文献

Selvadurai A P S. 2000. Partial Differential Equations in Mechanics［M］. Berlin： Springer-Verlag.

查找原文

参考文献

Terzaghi K. 1925. Erdbaumechanik auf Bodenphysikalischer Grundlage ［M］. Vienna： Leipzig Deuticke， 175-176.

查找原文

参考文献

Terzaghi K. 1943. Theoretical Soil Mechanics［M］. New York： John Wiley Sons.

查找原文

参考文献

Zienkiewicz O C， Chang C T， Bettes P. 1980. Drained， undrained， consolidation and dynamic behaviour assumptions in soils［J］. Geotechnique， 30（4）： 385‒396.

查找原文

参考文献

曹雪山，殷宗泽. 2009. 一维非饱和土固结简化计算的改进方法［J］. 公路交通科技， 26（10）： 1‒5.

查找原文

参考文献

关山海，谢康和，胡安峰. 2003. 低频循环荷载下地基一维固结性状分析［J］. 岩土力学， 24（5）： 849‒853.

查找原文

参考文献

胡国长，朱晓勇，薛建，刘瑾，江灿珲，陈志昊，王竑. 2022. 不同养护龄期下凹凸棒土改良黏性土三轴压缩试验研究［J］. 矿产勘查， 13（6）： 843‒852.

查找原文

参考文献

李伟，管育春，毛启贵，邹滔，徐巧，杨星. 2021. 大兴安岭中南段查干白旗岩体地质地球化学特征［J］. 矿产勘查， 12（4）： 839‒848.

查找原文

参考文献

刘文毅，何美香，孙宏伟，王良，李晓姣. 2022. 河南省光山县泼河岩体地质地球化学特征、成因分析及找矿潜力［J］. 矿产勘查， 13（8）： 1080‒1090.

查找原文

参考文献

温介邦，王跃伟，谢康和，胡安峰，应宏伟. 2008. 软土非线性固结计算若干表格及应用［J］. 岩土力学， 29（8）： 2163‒2169.

查找原文

参考文献

杨文强，何德洪. 2018. 填土地基建筑物纠倾及加固分析［J］. 矿产勘查， 9（4）： 720‒726.

查找原文

参考文献

殷宗泽，凌华. 2007. 非饱和土一维固结简化计算［J］. 岩土工程学报， 29（5）： 633‒637.

查找原文

参考文献

于雷，王建华，王广原. 2020. 应力水平影响下的软土边界面模型研究［J］. 矿产勘查， 11（4）： 818‒825.

查找原文

参考文献

张仪萍，严露，俞亚南，刘伟超. 2011. 真空预压加固软土地基变形与固结计算研究［J］. 岩土力学， 32（S1）： 149‒154.

查找原文

目录contents

摘要 Abstract
关键词 Keywords
0 引言
1 一维渗流固结解析解
1.1 基本假设
1.2 解析解的推导
1.3 解析解的求解流程
2 与已有解析解的对比
2.1 恒定荷载作用下解析解对比
2.2 时变荷载作用下解析解对比
3 结论
参考文献

摘要

现有的一维渗流固结解析解只适用于特定的荷载类型，如矩形分布荷载和三角形分布荷载，而工程实际中常见的是更为一般的荷载分布形式，而且荷载往往是随时间而变化的。为更好地便于工程应用，结合前人研究工作，本文在一定的假设基础上，采用理论分析方法明确了一维渗流固结问题对应的基本微分方程和相应的边界条件，然后采用特征函数法，推导出更为一般的随时间变化的荷载分布形式下一维固结解析解，并且对解析解进行编程求解。最后将新解析解与已有的特定荷载类型下的解析解进行对比，结果表明采用新解析解能够快速准确地得出一般时变荷载作用下的一维固结解析解，值得在工程应用中加以推广。

Abstract

The existing analytical solutions for one-dimensional seepage consolidation are only applicable to specific load types， such as rectangular and triangular distributed loads. However， in practical engineering scenarios， more general load distribution forms are common， and loads often vary with time. To facilitate engineering applications better， building upon previous research， this paper， under certain assumptions， employs theoretical analysis to delineate the fundamental differential equations and corresponding boundary conditions for the one-dimensional seepage consolidation problem. Subsequently， utilizing the method of characteristic functions， a more general analytical solution for one-dimensional consolidation under time-varying load distributions is derived， followed by programming to solve the analytical solution. Finally， the new analytical solution is compared with existing solutions for specific load types. The results demonstrate that employing the new analytical solution enables rapid and accurate determination of the one-dimensional consolidation analytical solution under general time-varying load conditions， thereby warranting its wider application in engineering contexts.

关键词

一维固结；解析解；一般时变荷载；特征函数法

Keywords

one dimensional consolidation ； analytical solution ； general time-varying load ； eigenfunction method

0 引言
固结计算在岩土工程设计尤其在地基处理方案的设计和选择工作中是至关重要的（杨文强和何德洪，2018；李伟等，2021；胡国长等，2022；刘文毅等，2022）。固结过程本质上是一个孔压逐渐转化为有效应力的过程。建立固结模型首先需要建立多相多孔介质运动方程。在热力学理论框架内，根据多孔介质热力学一致性原理，De Boer（2005）建立了对应的耦合偏微分方程组。显然，对该方程组进行求解即可以得到随时间和空间而变化的孔压和有效应力，相应的求解方法主要包括数值法和解析法两大类（殷宗泽和凌华，2007；温介邦等，2008；曹雪山和殷宗泽，2009；张仪萍等，2011；于雷等， 2020）。数值法适用范围广但工程应用不便。对三维情况下建立的偏微分运动方程组，显然直接用解析法求解是不现实的，为满足工程实用性的需求，可以做适当的假设，对偏微分运动方程组进行简化得出对应的微分方程，用解析法求解微分即变为可能。
假设流体只发生竖向渗流，土骨架只发生竖向位移，Terzaghi（1925）提出了经典的一维渗流固结理论。在该理论的基础上，Biot（1941）建立了三维渗漏固结理论，并且推导出了恒载作用下有限长土柱的一维渗流固结解析解。为考虑时变荷载的影响， Terzaghi（1943）提出了一种图解法。Olson（1977）提出了时变梯形荷载作用下的一维渗流固结图解法。 Zienkiewicz et al.（1980）提出了一种周期荷载作用下的一维渗流固结解析解，并且对解析解的有效性加以验证。针对矩形循环荷载情况，Baligh and Levadoux（1978）提出了循环荷载作用下非弹性正常固结黏土层的一维固结解析解，并且采用提出的解析解预测了大量循环荷载后黏土层发生的稳态超孔隙压力和沉降，并且与有限差分解进行了对比，结果表明解析解与有限差分解基本一致。此外，针对梯形循环荷载（Favaretti and Soranzo，1995）、三角形循环荷载（关山海等，2003）的情况，国内外学者也提出相应的一维渗流固结解析解。针对正弦循环荷载的情况，Geng et al.（2006）提出了一种固结半解析解，通过考虑土层的压缩性和渗透性的变化来解决一维非线性固结问题，并探讨了循环荷载下饱和软土一维非线性固结的相关行为。针对哈弗循环荷载的情况，Razouki et al.（2013）提出了一种固结非齐次偏微分方程的精确解析解。并且采用有限元数值解对解析解的有效性加以验证。
加载方式对地基沉降也有着较大影响。太沙基固结理论中假定外部荷载为瞬时一次性加载的，这显然与大多数工程实际加载情况不符合。近年来，中国轨道交通设施的建设一直处于持续发展的阶段。大量道路铁道、桥梁隧道建设的同时带来很多新的问题，比如交通荷载对地基固结行为的影响。因此，本文将循环荷载这一因素引入到固结问题的研究中，以期更清晰地了解间歇循环荷载对固结特性的影响。
综上，已有的解析解都只适用于特性类型的荷载情况，而实际过程中荷载往往是较为复杂的，而且是随时间而变化的。复杂时变荷载作用下的一维渗流固结解析解较难得出，但是其有较大的工程应用价值。考虑一般时变荷载作用下，本文设法引入特征函数法对一维渗流固结方程进行求解，得出相应解析解，并且结合已有的研究成果对解析解的准确性和有效性进行了验证。
1 一维渗流固结解析解
1.1 基本假设
按照De Boer（2005）的研究，为了便于三维情况下饱和土体渗流固结方程的建立，可以做如下假设：（1）土体完全饱和；（2）土颗粒和水均不可压缩；（3）忽略土水间的热量交换；（4）忽略水的黏滞力；（5）土体各向同性；（6）动力效应和对流效应可以忽略。在多孔介质热力学一致性原理基础上，即可以建立三维饱和土体渗流固结方程。
1.2 解析解的推导
考虑到三维渗流问题的复杂性，因此三维渗流问题所建立的偏微分方程一般采用数值法进行求解，如有限元法、有限差分法、边界元法等。然而数值法对实际操作人员的专业素养要求较高，如果操作人员对软件使用不当极有可能得出不合理的结果，而且对同一方程，不同人员即使采用同一软件求解得出的结果有时也不尽相同。因此，数值法对工程应用极为不便，为便于工程应用，在做合理简化和假设的情况下，求对应的解析解是十分有必要。
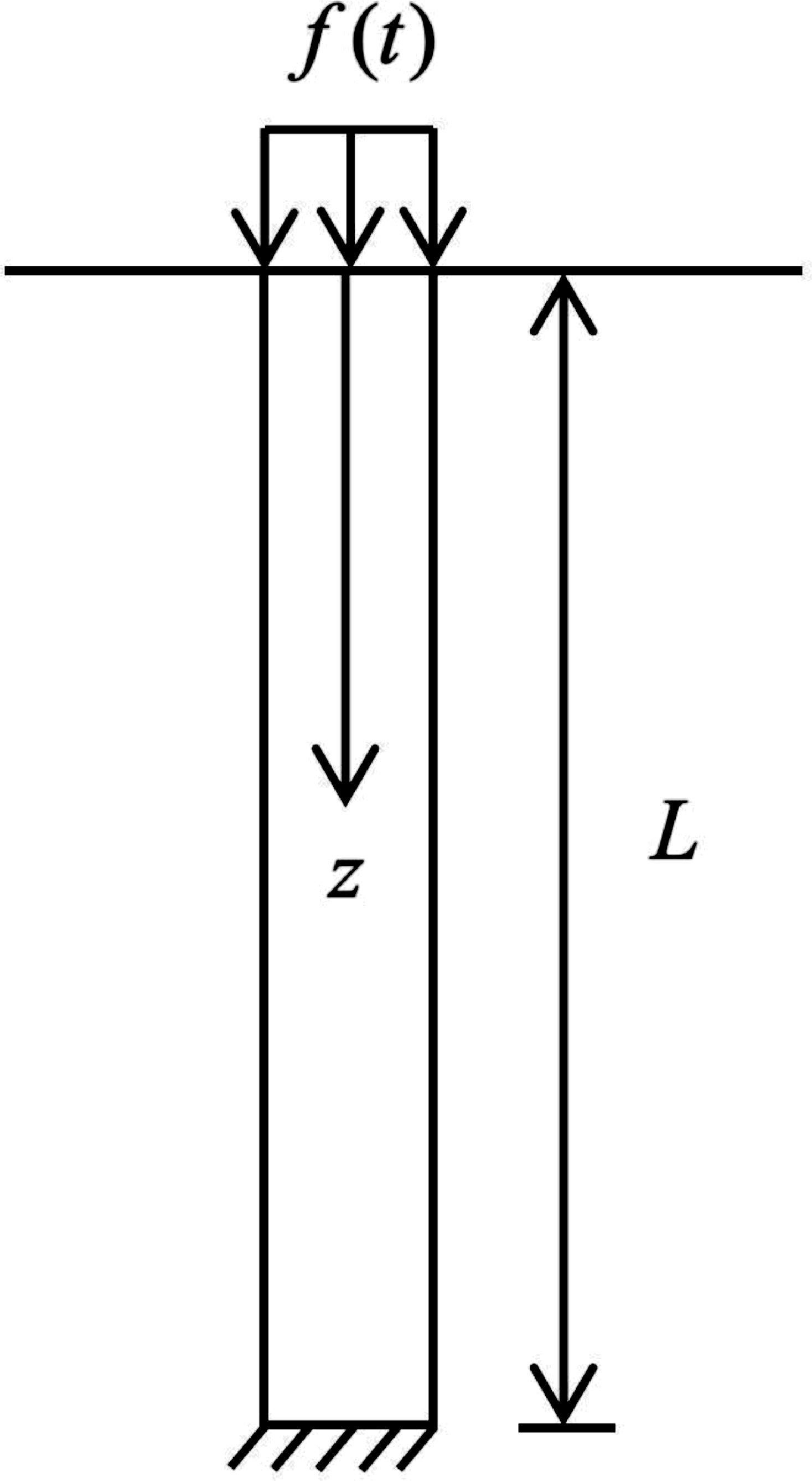
如图1所示，在一维小变形情况下，完全饱和土柱高 L。作用在土柱上边界的外荷载为时变荷载 f（t）。假定上侧边界完全排水，下侧边界固定且完全不排水，土骨架运动和水渗流只能沿竖直方向进行。假定孔隙水的渗流服从达西定律并且土体在固结过程中渗透系数、Lame常数和土体密度均不发生变化。此外可以假定水渗流和土位移竖直向下为正，土柱初始垂直位移为零。
一维渗流固结对应的基本微分方程为：
图1 一维渗流固结示意

(λ + 2 μ) \frac{\partial^{2} u (z, t)}{\partial z^{2}} - \frac{\partial p (z, t)}{\partial z} = 0

(1)

\frac{\partial^{2} u (z, t)}{\partial t \partial z} - \frac{k}{ρ g} \frac{\partial^{2} p (z, t)}{\partial z^{2}} = 0

(2)

式（1~2）中，z和t分别表示位置（m）和时间（d）； u（z，t）和 p（z，t）分别表示土骨架位移分布和孔压分布；λ 和 μ 表示 Lame 常数；k、ρ 和 g 分别表示渗透系数（m/d）、水的密度（kg/m³）和重力加速度（m/s²）。
根据微分方程求解过程可知，在求解由式（1）和式（2）组成的微分方程组前需要首先明确边界条件和初始条件。边界条件主要包括孔压边界、力边界和位移边界。

{p (z, t)|}_{z = 0} = 0

(3a)

{\frac{\partial p (z, t)}{\partial z}|}_{z = L} = 0

(3b)

{p (z, t)|}_{z = L} = 0

(3c)

{((λ + 2 μ) \frac{\partial u (z, t)}{\partial z})|}_{z = 0} = {σ (z, t)|}_{z = 0} = - f (t)

(4)

{u (z, t)|}_{z = L} = 0

(5)

初始条件包括初始位移条件和初始孔压条件

{u (z, t)|}_{t = 0} = 0

(6)

{p (z, t)|}_{t = 0} = f (0)

(7)

式（3b）对应的是底部完全不透水的孔压边界，当底部透水时，对应的孔压边界变为对一维渗流固结问题的求解即转化为了在边界条件式（3a）、式（3b）、式（4）、式（5），初始条件式（6）、式（7）条件下，求解式（1）和式（2）组成的偏微分方程组。
以z为变量，对式（1）进行一次积分易得

(λ + 2 μ) \frac{\partial u (z, t)}{\partial z} - p (z, t) = χ (t)

(8a)

代入边界条件式（3a）和式（4），易得

χ (t) = - f (t)

(8b)

所以，式（8a）转化为

(λ + 2 μ) \frac{\partial u (z, t)}{\partial z} - p (z, t) = - f (t)

(8c)

将式（8c）对时间t求偏导，易得

(λ + 2 μ) \frac{\partial^{2} u (z, t)}{\partial z \partial t} - \frac{\partial p (z, t)}{\partial t} = - f^{'} (t)

(9a)

将式（2）代入式（9a）得

\frac{\partial p (z, t)}{\partial t} = \frac{k (λ + 2 μ)}{ρ g} \frac{\partial^{2} p (z, t)}{\partial z^{2}} + f^{'} (t)

(9b)

令固结系数为

C_{v} = \frac{k (λ + 2 μ)}{ρ g}

(9c)

则式（9b）化为

\frac{\partial p (z, t)}{\partial t} = C_{v} \frac{\partial^{2} p (z, t)}{\partial z^{2}} + f^{'} (t)

(9d)

显然，如果能对式（9d）进行解析法求解即可以得出孔压分布 p（z，t），在已知孔压分布的情况下，结合式（8c）即可以得出土骨架位移分布。
为了求解如式（9d）所示的非齐次问题，可以先求解对应的齐次问题

\frac{\partial p (z, t)}{\partial t} = C_{v} \frac{\partial^{2} p (z, t)}{\partial z^{2}}

(9e)

考虑采用分离变量法（Selvadurai，2000；Logan， 2004），相应的特征函数为

y_{n} = s i n [\frac{(1 + 2 n) π z}{2 L}]

(10)

其中，n = 0，1，2. . .。孔压p（z，t）和外荷载对时间的一阶导数 f'（t）可以表示为特征函数 y_n 的线性组合，即

\begin{matrix} p (z, t) = \sum_{n = 0}^{\infty} p_{n} (t) y_{n} \\ = \sum_{n = 0}^{\infty} p_{n} (t) s i n [\frac{(1 + 2 n) π z}{2 L}] \end{matrix}

(11)

\begin{matrix} f^{'} (t) = \sum_{n = 0}^{\infty} f_{n} (t) y_{n} \\ = \sum_{n = 0}^{\infty} f_{n} (t) s i n [\frac{(1 + 2 n) π z}{2 L}] \end{matrix}

(12)

其中，p_n（t）和f_n（t）表示与特征函数式（10）对应的傅立叶系数。

f_{n} (t) = \frac{4 f^{'} (t)}{π (2 n + 1)}

(13)

为求出p_n（t）的表达式，将式（11）和式（12）代入式（9d）易得

p_{n}^{'} (t) + C_{v} {(\frac{(1 + 2 n) π}{2 L})}^{2} p_{n} (t) = f_{n} (t)

(13a)

η_{n} = C_{v} {(\frac{(1 + 2 n) π}{2 L})}^{2}

(13b)

则式（13a）化为

p_{n}^{'} (t) + η_{n} p_{n} (t) = f_{n} (t)

(13c)

将式（11）代入式（7）得

\sum_{n = 0}^{\infty} p_{n} (0) s i n [\frac{(1 + 2 n) π z}{2 L}] = f (0)

(14a)

所以

{p_{n} (t)|}_{t = 0} = \frac{4 f (0)}{π (2 n + 1)}

(14b)

考虑边值式（14b），对式（13c）所示的常微分方程进行求解易得

p_{n} (t) = \frac{4}{π (2 n + 1)} e^{- η_{n} t} f (0) + \int_{0}^{t} e^{- η_{n} (t - x)} f_{n} (x) d x

(15a)

将式（13）代入式（15a）易得

p_{n} (t) = \frac{4}{π (2 n + 1)} [e^{- η_{n} t} f (0) + \int_{0}^{t} e^{- η_{n} (t - x)} f^{'} (x) d x]

(15b)

在得出p_n（t）的情况下，代入式（11）容易得出随时间和空间位置而变化的孔压分布p（z，t）。
在推导式（15b）的过程中，一个核心的假设是时变外载f（t）是随时间逐渐光滑变化的。然而工程实际中外荷载随时间可能是非光滑变化的，例如阶跃循环荷载。为了将非光滑变化的时变外载f（t）表示为与光滑变化的时变外载类似的形式，引入 Heaviside阶跃函数H（•）

\begin{matrix} f (t) = f_{1} (t) [1 - H (t - t_{1})] \\ + \dots \sum_{i = 1}^{m - 1} f_{i + 1} (t) [H (t - t_{i}) - H (t - t_{i + 1})] \\ + f_{m + 1} (t) H (t - t_{m}) \end{matrix}

(16)

其中，f_i_{+ 1}（t）表示在时间段[t_i，t_i_{+ 1} ]内的连续时变荷载函数。考虑到 Heaviside 阶跃函数 H（•）满足当 x ≥ 0 时，H（ x）= 1；当 x <0 时，H（ x）= 0。显然，当时变荷载光滑变化时，式（16）退化为

f (t) = f_{1} (t)

(16a)

即退化为了随时间逐渐光滑变化的时变荷载形式。对式（16）求导易得

\begin{matrix} f^{'} (t) = f_{1}^{'} (t) [1 - H (t - t_{1})] - \\ f_{1} (t) δ (t - t_{1}) + \dots \\ \sum_{i = 1}^{m - 1} \{f_{i + 1}^{'} (t) [H (t - t_{i}) - H (t - t_{i + 1})]\} + \\ \sum_{i = 1}^{m - 1} \{f_{i + 1} (t) [δ (t - t_{i}) - δ (t - t_{i + 1})]\} + \\ f_{m + 1}^{'} (t) H (t - t_{m}) + f_{m + 1} (t) δ (t - t_{m}) \end{matrix}

(17)

其中，狄拉克三角函数δ（t）满足

\begin{matrix} \int_{m_{1}}^{m_{2}} f (x) δ (x - x_{0}) d x = \\ \{\begin{matrix} f (x_{0}) & x_{0} \in (m_{1}, m_{2}) \\ 0 & x_{0} \in (- \infty, m_{1}) \cup (m_{2}, + \infty) \end{matrix} \end{matrix}

(18)

显然，满足 H'（t）= δ（t）。当荷载 f（t）是随时间非光滑变化时，在采用式（15b）求解p_n（t）时，需要将式（17）代替光滑变化的 f（t）。根据式（15b）得出 p_n（t）后，代入式（11）即可得出p（z，t）。
在得出随时间和空间变化的孔压 p（z，t）后，将其代入式（8c），然后对z求积分易得

\begin{matrix} u (z, t) = \frac{- 1}{λ + 2 μ} \sum_{n = 0}^{\infty} \frac{2 L}{(1 + 2 n) π} p_{n} (t) c o s [\frac{(1 + 2 n) π z}{2 L}] - \\ \frac{f (t)}{λ + 2 μ} z + c \end{matrix}

(19a)

其中，c 表示积分常数。考虑到边界条件式（5），易得积分常数为

c = \frac{L f (t)}{λ + 2 μ}

(19b)

所以式（19a）转化为

\begin{matrix} u (z, t) = \frac{- 1}{λ + 2 μ} \sum_{n = 0}^{\infty} \frac{2 L}{(1 + 2 n) π} p_{n} (t) c o s [\frac{(1 + 2 n) π z}{2 L}] + \\ \frac{f (t) (L - z)}{λ + 2 μ} \end{matrix}

(19c)

1.3 解析解的求解流程
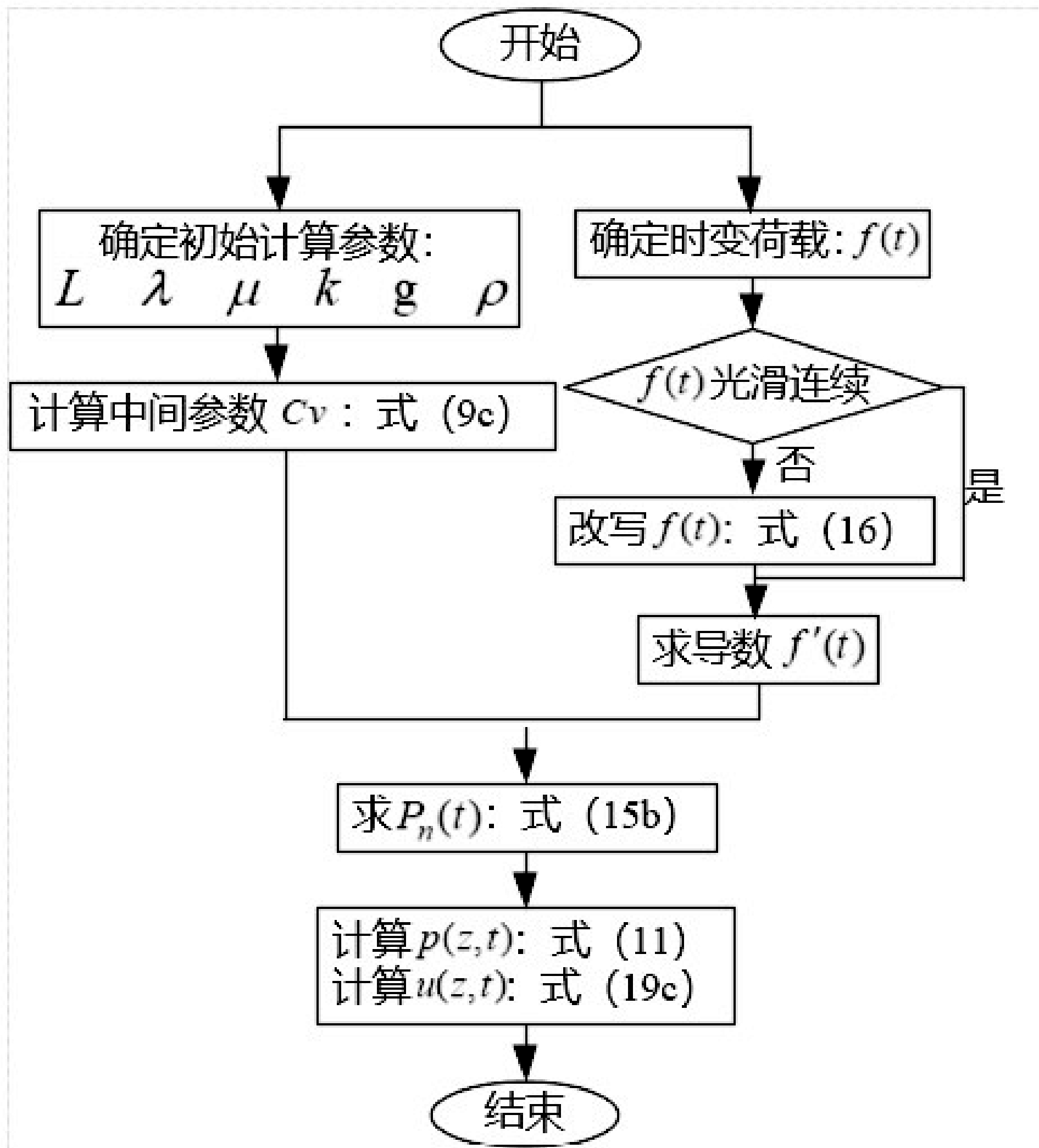
综上，在实际工程应用中为了求出一般时变荷载 f（t）作用下饱和土体内的孔压分布 p（z，t）和土骨架位移分布 u（z，t），可以按照如图2 所示的步骤进行：
（1）确定初始计算参数。主要包括饱和土柱柱长 L（m）、拉梅常数 λ和 μ、达西渗透系数 k（m/d）、重力加速度 g（m/s²）、水密度 ρ（kg/m³）。根据式（9c）计算得出中间参数C_v。
（2）确定时变荷载及表达式。当时变荷载连续光滑时，直接使用其表达式；当时变荷载非连续光滑时，根据式（16）改写时变荷载的表达式。然后计算得出时变荷载f（t）的导数f'（t）。
（3）按照式（15b）计算p_n（t）。
（4）按照式（11）计算孔压分布 p（z，t），按照式（19c）计算土骨架位移分布u（z，t）。
图2 新解析法求解流程
2 与已有解析解的对比
2.1 恒定荷载作用下解析解对比
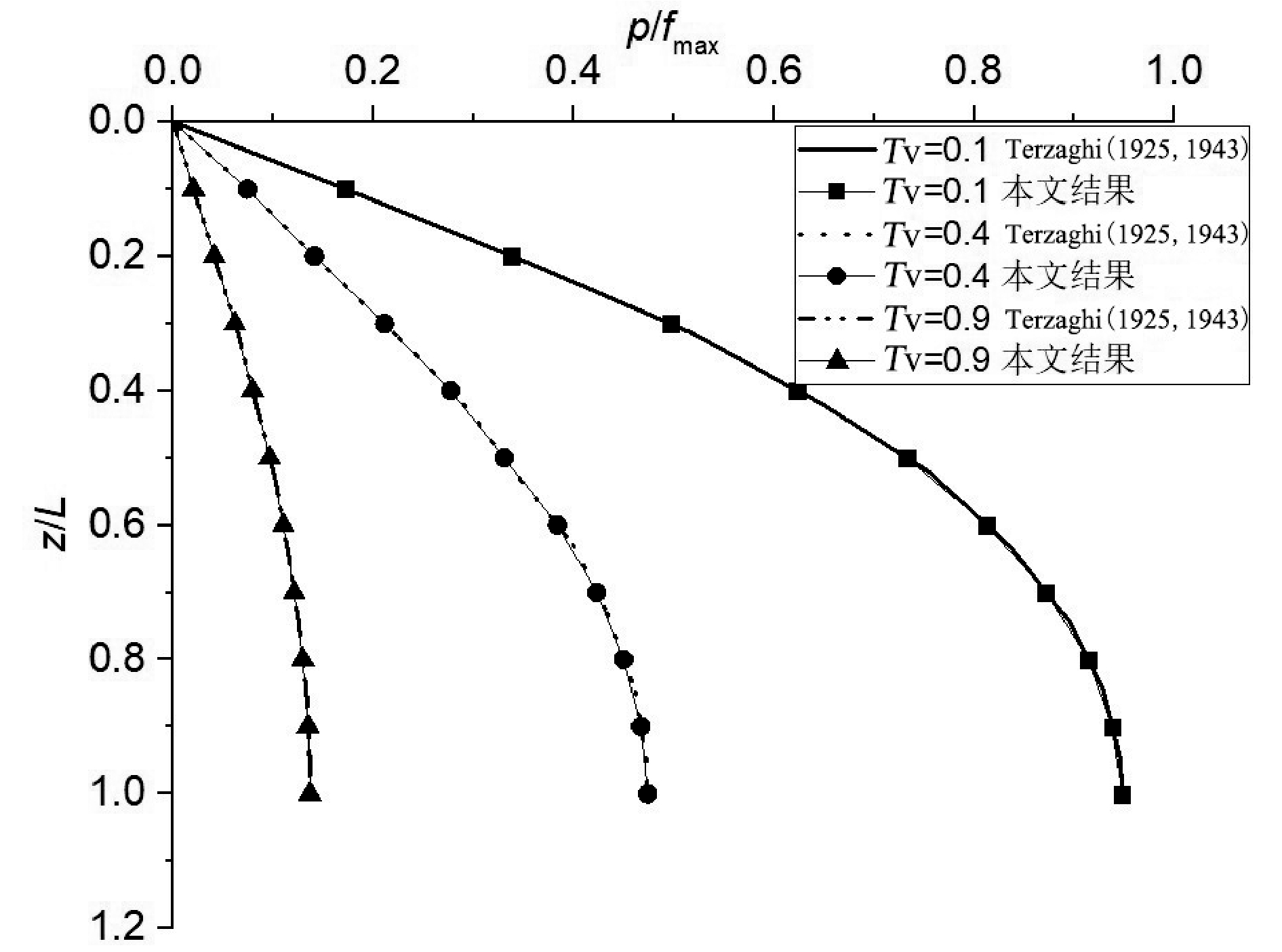
在恒定荷载作用下 Terzaghi（1925，1943）推导提出了一维固结经典解析解。按照1.3节的求解流程进行求解容易得出如图3所示的结果。为使结果具有可比性，将横纵坐标均进行无量纲化，横坐标为孔压 p 与荷载 f_max比值，纵坐标为计算点坐标 z 与饱和土柱柱长 L 的比值，表中时间因数取值为 T_v = c_vt/L²，从图中可以看出，本文解析解与已有解析解具有完全相同的计算精度。这主要是因为，已有解析解本质采用的是太沙基固结理论，而太沙基固结理论解析解释本文解析解的特例。这可以直接表明，本文得出的固结解析解完全适用于恒定荷载的情况，这主要是因为恒定荷载本质是时变荷载的一种特例。
2.2 时变荷载作用下解析解对比
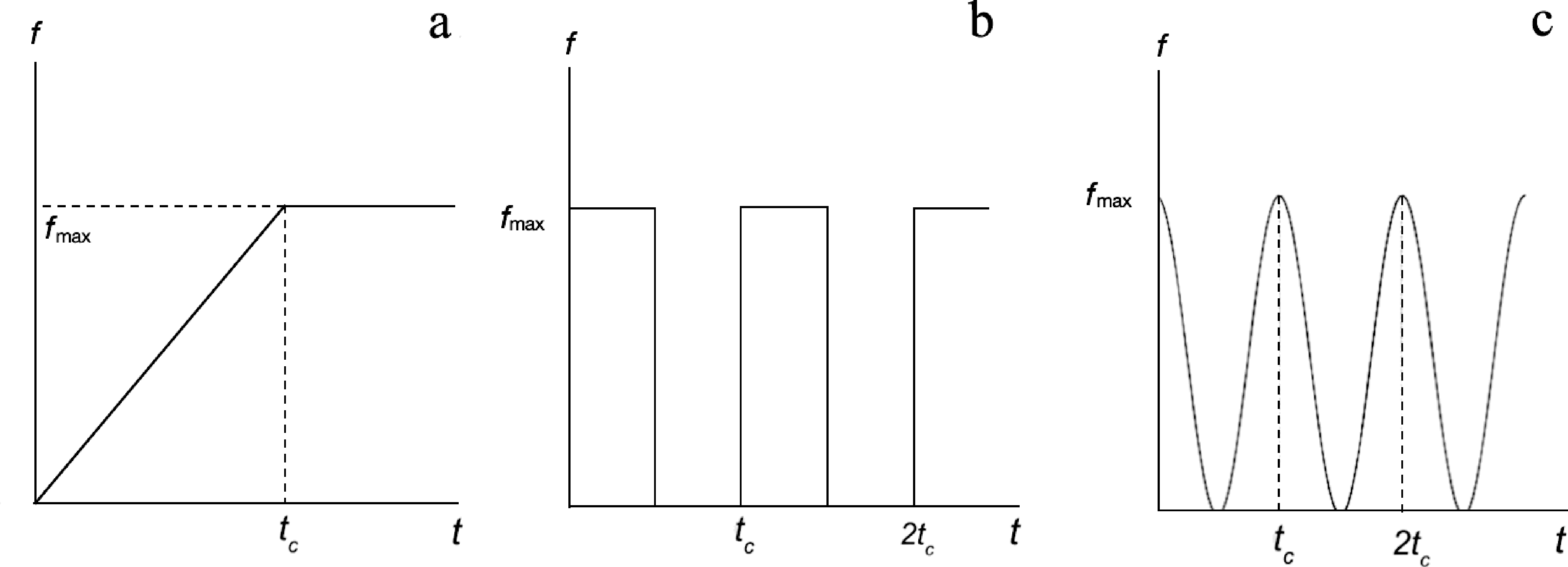
从图2 的求解过程可以明显看出，时变荷载作用下新解析法计算过程比恒载作用下新解析法计算过程更为复杂，需要首先对时变荷载的表达式进行适当的处理。考虑到目前典型的时变荷载主要包括梯形荷载、阶跃循环荷载和哈弗辛循环荷载，其他类型的时变荷载可以通过这三类荷载叠加得出。因此本文考虑如图4 所示的经典的梯形荷载、阶跃循环荷载、哈弗辛循环荷载3种情况，采用新解析法进行计算，并且将计算结果与已有解析解计算结果对比，以验证新解析解的广泛有效性。
图3 恒载作用下结果对比
对如图所示的梯形荷载（图4a），在时间段（0，t_c）内由 0 线性增加至 f_max，之后保持 f_max 值不变。显然，该荷载为分段光滑荷载，按照图2所示的新解析法求解流程，显然应该先对分段光滑荷载进行连续化处理。结合 Heaviside 阶跃函数后梯形荷载的函数表达式可以表示为：

f (t) = \frac{f_{m a x} t}{t_{c}} [1 - H (t - t_{c})] + f_{m a x} H (t - t_{c})

(20)

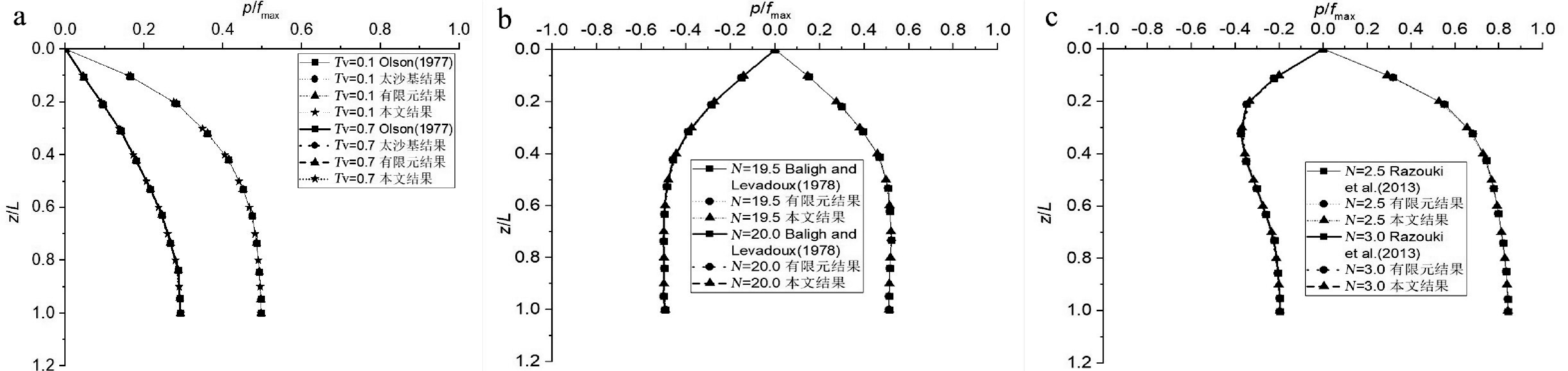
然后按照1.3节的求解流程即可以得出如图（5a）所示的孔压分布结果，与已有研究成果（Olson， 1977）、太沙基渗流固结理论计算结果、有限元计算结果的对比也在图中体现，图中计算时取 t_c = 0.2L² /c_v。从图5a中可以看出新解析法与已有解析法、太沙基渗流固结理论计算法、有限元法具有相同的精度，这主要是因为太沙基渗流固结理论计算法本质上是本文解析法的特例。这可以直接表明本文所提出的新的固结解析解适用于梯形荷载时变荷载的情形。
图4 三种典型时变荷载
a—梯形荷载；b—阶跃循环荷载；c—哈弗辛循环荷载
图5 三种典型时变荷载下计算结果对比
a—梯形荷载；b—阶跃循环荷载；c—哈弗辛循环荷载
对如图4b 所示的阶跃式循环荷载情况（Baligh and Levadoux，1978），循环周期为 t_c，荷载最大值为 f_max。将分段光滑的阶跃式循环荷载函数，采用 Heaviside阶跃函数进行光滑化处理，可以得出阶跃式循环时变荷载可以表示为：

\begin{matrix} f (t) = f_{m a x} [1 - H (t - \frac{t_{c}}{2})] + \\ \sum_{i = 1}^{s} f_{m a x} \{H (t - i t_{c}) - H [t - (i + \frac{1}{2}) t_{c}]\} \end{matrix}

(21)

求导后易得

\begin{matrix} f^{'} (t) = - f_{m a x} δ (t - \frac{t_{c}}{2}) + \\ \sum_{i = 1}^{s} f_{m a x} \{δ (t - i t_{c}) - δ [t - (i + \frac{1}{2}) t_{c}]\} \end{matrix}

(22)

将式（22）代入式（15b）易得

p_{n} (t) = \frac{4 f_{m a x}}{π (2 n + 1)} [e^{- η_{n} t} + h (t)]

(23)

其中，当满足mt_c <t ≤（m + 0.5）t_c时
$h (t) = \sum_{i = 0}^{m - 1} [e^{- η_{n} [t - (i + 1) t_{c}]} - e^{- η_{n} [t - (i + 0.5) t_{c}]}]$
当满足mt_c<t ≤（m + 0.5）t_c时
$\begin{matrix} h (t) = \sum_{i = 0}^{m - 1} [e^{- η_{n} [t - (i + 1) t_{c}]} - e^{- η_{n} [t - (i + 0.5) t_{c}]}] \\ - e^{- η_{n} [t - (m + 0.5) t_{c}]} \end{matrix}$
再次将式（23）代入式（11）和式（19c）就可分别得到孔压分布和土体位移分布。
当周期满足t_c = 0.1L² /c_v时，本文得出的解析解与已有解析解（Baligh and Levadoux，1978）、有限元计算结果的对比如图5b 所示，图中 N 表示循环周次。从图5b可以明显看出，对阶跃式循环时变荷载的情形，本文解析法的精度和有效性并不低于已有的方法和有限元法。这可以直接表明本文所提出的新的固结解析解适用于阶跃式循环时变荷载的情形。
对如图4a 所示的在公路铁路路面荷载计算时常用的哈弗辛循环荷载情况（Razouki et al.，2013），循环周期为 t_c，荷载最小值为 0，荷载最大值为 f_max。哈弗辛循环荷载为一阶连续的时变荷载，因此无需 Heaviside 阶跃函数进行光滑化处理。哈弗辛循环时变荷载可以表示

f (t) = f_{m a x} {s i n}^{2} (\frac{t}{t_{c}} π)

(24)

然后按照1.3节的求解流程即可以得出如图5c 所示的孔压分布结果，与已有研究成果（Razouki et al.，2013）、有限元计算结果的对比也在图中体现，图中计算时取t_c = 0.1L² /c_v。从图中可以看出，对哈弗辛循环时变荷载情况，新解析法与已有解析法、有限元法具有相同的精度。这可以直接表明本文所提出的新的固结解析解适用于哈弗辛循环时变荷载情况。
综合图5a~c 可以明显看出，无论对恒定荷载，还是梯形荷载、阶跃循环荷载、哈弗辛循环荷载3种时变荷载，本文所提出的新的解析法的精度和有效性均很高，与已有的只适用于特定荷载类型的解析法计算结果基本完全一致。但是从本文适用于一般时变荷载情况的一维固结解析解的推导过程可以看出，本文的解析解适用于更为一般化的时变荷载情形，不论时变荷载是否一阶连续均可。对一阶不连续的时变荷载，只需采用Heaviside阶跃函数进行光滑化处理即可。考虑到本文所提出的新解析解适用于一般的时变荷载情况，显然该解析解的应用范围更加广泛，工程实用性更强，建议可以在工程设计工作中加以参考。
3 结论
现有的一维渗流固结解析解只适用于特定的时变荷载类型，然而实际工程中的时变荷载往往是较为复杂的，得出一种适用于一般时变荷载类型的一维渗流固结解析解显然具有十分重要的工程价值。本文在前人相关研究工作的基础上，考虑更为一般的时变荷载情况，采用特征函数法对一维渗流固结微分方程进行求解，得出了新的适用于一般时变荷载情况的渗流固结解析解。通过与前人研究成果、有限元计算结果的对比验证本文新解析解的有效性、适用范围的广泛性以及精度。主要得出结论如下：
（1）无论对恒定荷载，还是梯形荷载、阶跃循环荷载、哈弗辛循环荷载3种时变荷载，本文新提出的解析法都是有效的，而且具有较高的精度。
（2）新解析解适用于更为一般的时变荷载情况，包括连续荷载和阶跃式荷载，工程实用性更强，建议在后续的工程设计工作中可加以推广应用。
本文的研究工作是建立在小变形、渗流符合达西定律、一维固结 3 个假设的基础之上的。然而实际工程问题不一定符合这 3 个假设，建议后续可以采用类似本文的研究方法开展一般时变荷载作用下的大变形、平面或三维、非达西渗流固结解析解或半解析解的研究。
参考文献
- Baligh M M， Levadoux J N. 1978. Consolidation theory for cyclic loading［J］. Journal of the Geotechnical Engineering Division， 104（4）： 415‒431.
- Biot M A. 1941. General theory of three-dimensional consolidation［J］. Journal of Applied Physics， 12（2）： 155‒164.
- De Boer R. 2005. Trends in Continuum Mechanics of Porous Media［M］. Berlin： Springer Science & Business Media.
- Favaretti M， Soranzo M. 1995. A simplified consolidation theory in cyclic loading conditions［C］//Compression and Consolidation of Clayey Soils， 405‒409. Netherlands： Balkema.
- Geng X， Xu C， Cai Y. 2006. Non-linear consolidation analysis of soil with variable compressibility and permeability under cyclic loadings［J］. International Journal for Numerical & Analytical Methods in Geomechanics， 30（8）： 803‒821.
- Logan J D. 2004. Applied Partial Differential Equations［M］. NewYork： Springer-Verlag.
- Olson R E. 1977. Consolidation under time dependent loading［J］. Journal of the Geotechnical Engineering Division， 103（1）： 55‒60.
- Razouki S S， Bonnier P， Datcheva M， Schanz T. 2013. Analytical solution for 1D consolidation under haversine cyclic loading［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 37（14）： 2367‒2372.
- Selvadurai A P S. 2000. Partial Differential Equations in Mechanics［M］. Berlin： Springer-Verlag.
- Terzaghi K. 1925. Erdbaumechanik auf Bodenphysikalischer Grundlage ［M］. Vienna： Leipzig Deuticke， 175-176.
- Terzaghi K. 1943. Theoretical Soil Mechanics［M］. New York： John Wiley Sons.
- Zienkiewicz O C， Chang C T， Bettes P. 1980. Drained， undrained， consolidation and dynamic behaviour assumptions in soils［J］. Geotechnique， 30（4）： 385‒396.
- 曹雪山，殷宗泽. 2009. 一维非饱和土固结简化计算的改进方法［J］. 公路交通科技， 26（10）： 1‒5.
- 关山海，谢康和，胡安峰. 2003. 低频循环荷载下地基一维固结性状分析［J］. 岩土力学， 24（5）： 849‒853.
- 胡国长，朱晓勇，薛建，刘瑾，江灿珲，陈志昊，王竑. 2022. 不同养护龄期下凹凸棒土改良黏性土三轴压缩试验研究［J］. 矿产勘查， 13（6）： 843‒852.
- 李伟，管育春，毛启贵，邹滔，徐巧，杨星. 2021. 大兴安岭中南段查干白旗岩体地质地球化学特征［J］. 矿产勘查， 12（4）： 839‒848.
- 刘文毅，何美香，孙宏伟，王良，李晓姣. 2022. 河南省光山县泼河岩体地质地球化学特征、成因分析及找矿潜力［J］. 矿产勘查， 13（8）： 1080‒1090.
- 温介邦，王跃伟，谢康和，胡安峰，应宏伟. 2008. 软土非线性固结计算若干表格及应用［J］. 岩土力学， 29（8）： 2163‒2169.
- 杨文强，何德洪. 2018. 填土地基建筑物纠倾及加固分析［J］. 矿产勘查， 9（4）： 720‒726.
- 殷宗泽，凌华. 2007. 非饱和土一维固结简化计算［J］. 岩土工程学报， 29（5）： 633‒637.
- 于雷，王建华，王广原. 2020. 应力水平影响下的软土边界面模型研究［J］. 矿产勘查， 11（4）： 818‒825.
- 张仪萍，严露，俞亚南，刘伟超. 2011. 真空预压加固软土地基变形与固结计算研究［J］. 岩土力学， 32（S1）： 149‒154.

图1 一维渗流固结示意

图2 新解析法求解流程

图3 恒载作用下结果对比

图4 三种典型时变荷载

图5 三种典型时变荷载下计算结果对比

相似文献

基本信息

中图分类号: TU431
文献标识码: A
DOI: 10.20008/j.kckc.202406019
文章编号: 1674-7801(2024)06-1084-08

基金信息

本文受国家自然科学基金项目（41372328）资助；

引用信息

卢许佳，杨润基，高庆，谭维佳. 2024. 适用于一般时变荷载情况的一维固结解析解［J］. 矿产勘查，15（6）：1084-1091.

Lu Xujia，Yang Runji，Gao Qing，Tan Weijia. 2024. One dimensional analytical solution of consolidation for general time-varying load cases［J］. Mineral Exploration，15（6）：1084-1091.

稿件历史

收稿日期: 2022-11-21

参考文献

Baligh M M， Levadoux J N. 1978. Consolidation theory for cyclic loading［J］. Journal of the Geotechnical Engineering Division， 104（4）： 415‒431.
Biot M A. 1941. General theory of three-dimensional consolidation［J］. Journal of Applied Physics， 12（2）： 155‒164.
De Boer R. 2005. Trends in Continuum Mechanics of Porous Media［M］. Berlin： Springer Science & Business Media.
Favaretti M， Soranzo M. 1995. A simplified consolidation theory in cyclic loading conditions［C］//Compression and Consolidation of Clayey Soils， 405‒409. Netherlands： Balkema.
Geng X， Xu C， Cai Y. 2006. Non-linear consolidation analysis of soil with variable compressibility and permeability under cyclic loadings［J］. International Journal for Numerical & Analytical Methods in Geomechanics， 30（8）： 803‒821.
Logan J D. 2004. Applied Partial Differential Equations［M］. NewYork： Springer-Verlag.
Olson R E. 1977. Consolidation under time dependent loading［J］. Journal of the Geotechnical Engineering Division， 103（1）： 55‒60.
Razouki S S， Bonnier P， Datcheva M， Schanz T. 2013. Analytical solution for 1D consolidation under haversine cyclic loading［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 37（14）： 2367‒2372.
Selvadurai A P S. 2000. Partial Differential Equations in Mechanics［M］. Berlin： Springer-Verlag.
Terzaghi K. 1925. Erdbaumechanik auf Bodenphysikalischer Grundlage ［M］. Vienna： Leipzig Deuticke， 175-176.
Terzaghi K. 1943. Theoretical Soil Mechanics［M］. New York： John Wiley Sons.
Zienkiewicz O C， Chang C T， Bettes P. 1980. Drained， undrained， consolidation and dynamic behaviour assumptions in soils［J］. Geotechnique， 30（4）： 385‒396.
曹雪山，殷宗泽. 2009. 一维非饱和土固结简化计算的改进方法［J］. 公路交通科技， 26（10）： 1‒5.
关山海，谢康和，胡安峰. 2003. 低频循环荷载下地基一维固结性状分析［J］. 岩土力学， 24（5）： 849‒853.
胡国长，朱晓勇，薛建，刘瑾，江灿珲，陈志昊，王竑. 2022. 不同养护龄期下凹凸棒土改良黏性土三轴压缩试验研究［J］. 矿产勘查， 13（6）： 843‒852.
李伟，管育春，毛启贵，邹滔，徐巧，杨星. 2021. 大兴安岭中南段查干白旗岩体地质地球化学特征［J］. 矿产勘查， 12（4）： 839‒848.
刘文毅，何美香，孙宏伟，王良，李晓姣. 2022. 河南省光山县泼河岩体地质地球化学特征、成因分析及找矿潜力［J］. 矿产勘查， 13（8）： 1080‒1090.
温介邦，王跃伟，谢康和，胡安峰，应宏伟. 2008. 软土非线性固结计算若干表格及应用［J］. 岩土力学， 29（8）： 2163‒2169.
杨文强，何德洪. 2018. 填土地基建筑物纠倾及加固分析［J］. 矿产勘查， 9（4）： 720‒726.
殷宗泽，凌华. 2007. 非饱和土一维固结简化计算［J］. 岩土工程学报， 29（5）： 633‒637.
于雷，王建华，王广原. 2020. 应力水平影响下的软土边界面模型研究［J］. 矿产勘查， 11（4）： 818‒825.
张仪萍，严露，俞亚南，刘伟超. 2011. 真空预压加固软土地基变形与固结计算研究［J］. 岩土力学， 32（S1）： 149‒154.

分享给微信好友或者朋友圈

使用微信“扫一扫”功能。

适用于一般时变荷载情况的一维固结解析解

One dimensional analytical solution of consolidation for general time-varying load cases

摘要

Abstract

关键词

Keywords

0 引言

1 一维渗流固结解析解

1.1 基本假设

1.2 解析解的推导

(1)

(2)

(3a)

(3b)

(3c)

(4)

(5)

(6)

(7)

(8a)

(8b)

(8c)

(9a)

(9b)

(9c)

(9d)

(9e)

(10)

(11)

(12)

(13)

(13a)

(13b)

(13c)

(14a)

(14b)

(15a)

(15b)

(16)

(16a)

(17)

(18)

(19a)

(19b)

(19c)

1.3 解析解的求解流程

2 与已有解析解的对比

2.1 恒定荷载作用下解析解对比

2.2 时变荷载作用下解析解对比

(20)

(21)

(22)

(23)

(24)

3 结论

参考文献

相似文献

基本信息

基金信息

引用信息

稿件历史

参考文献