0 引言

公路、水电、露天矿等工程的建设与实施，会大量开挖山体，从而形成大量的人工边坡。边坡开挖会对原始斜坡体产生卸荷效应，降低了土坡抵抗外界荷载的能力，从而影响工程质量和完整程度（倪振强等，2011），因此对卸荷后的边坡稳定性进行研究具有重要意义。目前国内外研究了多种评估开挖卸荷后的边坡稳定性的方法，其中主要的两类：直接核算开挖后土坡的稳定性和评估其在外荷载作用下（降雨、地震等）的稳定性。根据调查，降雨是目前山体或边坡破坏最主要的因素之一 （Olivares et al.，2014；Li et al.，2020），尤其是南方一些具有典型降雨气候和诱发山洪地貌的地区，降雨诱发边坡和山洪灾害频率高发，因此研究坡体卸荷和降雨入渗后边坡稳定性具有重要意义（Cho， 2014；Peres and Cancelliere，2016）。

目前，国内外通常采用数值模拟的方法来分析边坡的稳定性，其常用的数值理论包括有限元法 （蒋琳琳和赵川，2019）、有限差分法（蔡军和许胜才，2021）、离散元法（何怡等，2016）等。代雪和张家明（2021）基于Geostudio、理正软件以及ANSYS软件，采用 M-P 法、Bishop 法和强度折减法进行边坡稳定分析；高丙丽（2012）采用三维有限元法，分析了某水电工程右岸厂房后边坡的稳定性，得到了边坡开挖卸荷、支护中的变形规律和应力分布特性； 骆文进等（2020）基于 FLAC2D 仿真计算软件，对某水利工程沿线易受降雨入渗影响而诱发滑坡的黄土边坡进行数值模拟，评估边坡稳定性安全系数受设计坡比和降雨入渗深度的影响程度；李龙起等 （2020）以四川省古蔺县竹林沟滑坡为例，结合离散元 PFC2D 虚拟双轴压缩试验对坡体微观力学参数进行标定，随后建立 1∶1 数值计算模型进行稳定性计算，并记录坡体运动过程中应力及位移变化的情况。此外，还有部分学者在以上理论基础上采用新的数值分析技术对边坡开挖和降雨入渗稳定性进行了分析（Yang et al.，2019；Pan et al.，2020；程彬和卢靖，2020；张永雨，2020；Guo et al.，2021；刘玉叶等，2021）。

前人对边坡开挖稳定性分析和土坡降雨入渗分析进行了很好的研究，然而通过文献分析发现，还存在需要补充研究的地方：（1）大多数土坡在天然状态下处于非饱和状态，因此在数值分析时，需要考虑地下水位深度和真实孔隙水压分布；（2）由于土为非饱和土，因此常规数值方法采用的摩尔库伦模型来描述非饱和土的抗剪强度变化会造成一定误差；（3）在对边坡进行降雨入渗分析时，采用的降雨强度为年平均或者一时段之间的平均值，而这种方法通常忽略了循环降雨荷载对边坡稳定性的影响。根据以上问题，本文采用非饱和土抗剪强度理论，结合Morgenstern-Price条分法，对不同放坡角度下边坡的稳定性进行分析，同时采用具有不同降雨峰值的两组 72 h实测降雨值，动态分析了边坡安全系数，同时探讨了孔隙水压力的变化规律，研究结果可为相关工程提供参考。

1 工程地质及水文概况

研究区位于福建省溪南镇（图1），年降雨量 1700 mm 左右，根据当地气象台资料多年年平均降雨量为1610. 08 mm（1971—2012年），最大年降雨量2356.6 mm（1998 年），年降雨量具有分配不均的特征，每年 4—6 月份降雨量较集中，降水量占全年总量的51.3%，为丰水期；11月—翌年2月，为枯水期，降水量占总量的9.6%，其余为平水期。最小年降雨量 1046.2 mm（1963 年），最大日暴雨量 208.9 mm，最大时降雨量58.7 mm，年平均降雨天数142 d。

工程区内土层按其透水性可划分为相对透水层和相对隔水层2种。相对透水层由第四系上更新统冲积层中的粉细砂层构成，具弱—强透水性，而相对隔水层由第四系上更新统冲积层的黏土、含淤泥质壤土等构成，具极微—弱透水性。区内地下水赋存于砂性土层及基岩裂隙中。地下水随季节变化与地表水呈互补关系，雨季（4—9月）地下水位较高，旱季（10月—次年 3月）地下水位较低。本地区有关资料显示，场地地下水位的年变化幅度为 1～2 m。

a—现场工程区内典型边坡；b—研究区位置

2 非饱和土抗剪切强度

当土颗粒之间的孔隙充满水时，土体处于饱和状态，而当部分孔隙被空气充满时，土体处于非饱和状态。根据现场测量，边坡 3 种土样的饱和度平均值均小于 85%，此外降雨入渗是典型的非饱和流固耦合问题，因此采用非饱和强度理论来研究边坡稳定性更具合理性。为简单起见，地下水位以下的土通常假设为由有效应力控制，而地下水位以上的非饱和土由 2 个独立的应力变量控制，即净正应力和基质吸力。

为描述这一关系，有研究提出用 2 个独立的应力状态变量（ σ_f-u_a）和（u_a-u_w）来解释不饱和土抗剪强度变化规律（黎玺克，2021；刘顺青等，2022）：

式（1）中，τ_f是破坏面上的剪应力（kPa），c'是有效抗剪强度（kPa），其中净法向应力和破坏时的基质吸力等于零。 u_af 是破坏面的孔隙空气压力 （kPa），ϕ'是与净正应力状态变量相关的内摩擦角（°）；${\left(u_a-u_w\right)}_f$ 是失效面上的基质吸力，ϕ^b 表示剪切强度与基质吸力增速相关的角度（°）；σ_f是破坏面上的正应力（kPa）。

3 数值模型与计算参数

3.1 剖面选取

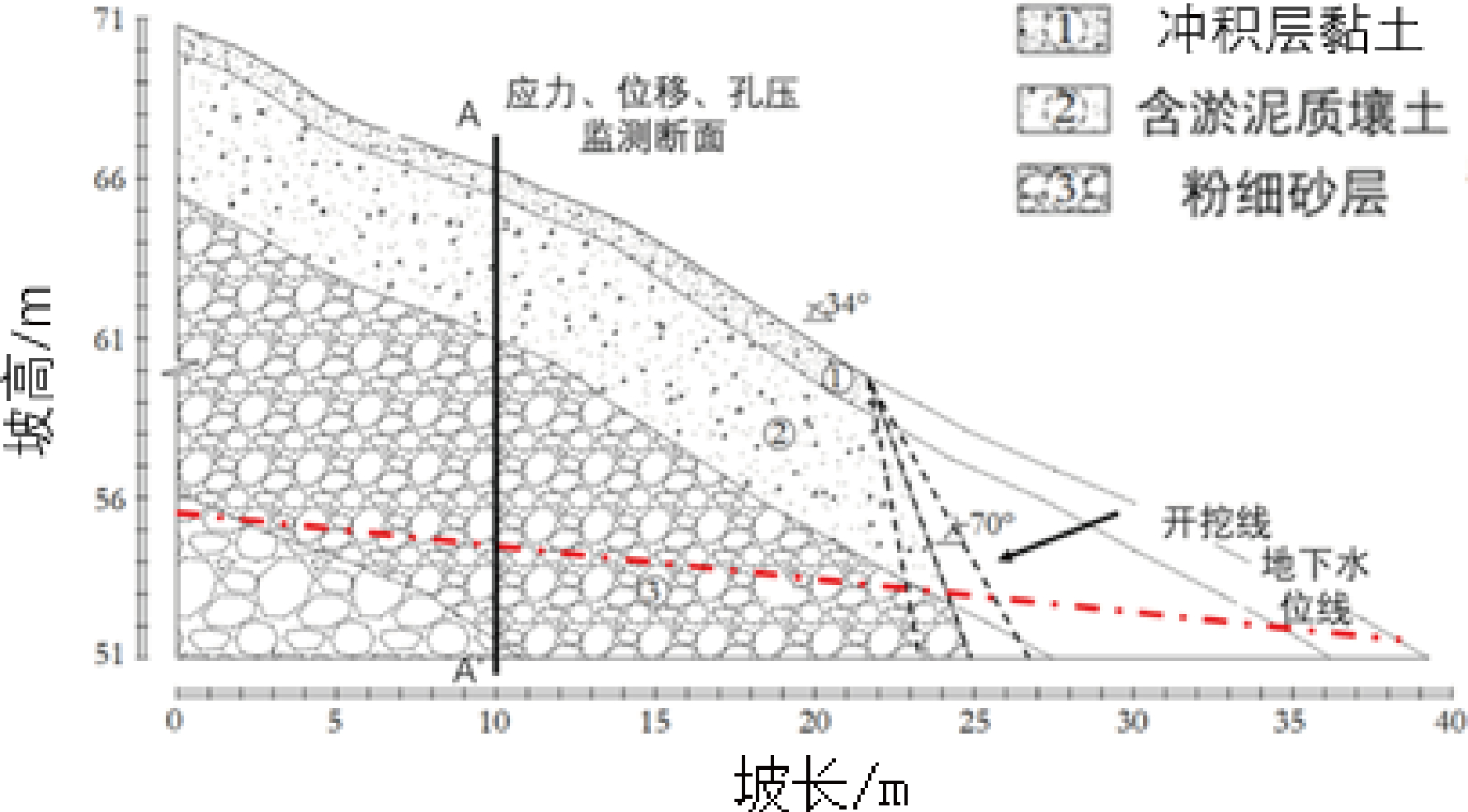
本文计算的边坡剖面如图2 所示，为研究区典型边坡。上覆土层为冲积层黏土，中部土层为含淤泥质壤土，第三层为粉细砂层，最底部为不透水基岩。根据室内试验结果，第四系冲积层黏土干密度为 1.17～1.57 g/cm³，孔隙比 0.720～1.333，压缩系数 0.26～0.63 MPa^-1，中等压缩性，局部高压缩性，饱和固结快剪内摩擦角 φ 值 19.3°～30.3°，快剪强度 c 值 17.1～28.9 kPa，标准贯入试验锤击数 10～14击。淤泥质壤土：软塑—软可塑状，具高压缩性，标准贯入试验锤击数 3～5 击。粉细砂：以粉砂、细砂为主，偶夹细砾层，结构密实。标准贯入试验锤击数 6～13 击。本次削坡共设置 3 个坡角，削坡后边坡坡角 β分别为 65°、70°、75°，AA’为数值计算中应力、位移、孔压监测断面，距离左下角零点10 m。

3.2 数值方法及模型

本研究采用 geo-studio 软件对边坡稳定性进行分析，而研究采用Morgenstern-Price方法进行计算，由于篇幅原因，此处不再给出详细推导M-P条分法的计算过程。SEEP/W 模块则是基于达西定律来描述土体内部的非饱和流动。为了解决非饱和流动问题，SEEP/W 使用了 2 个函数：导水函数和土水特征曲线。最大负孔隙水压力的大小取决于导水函数的形状，受渗透速率较小。土壤在孔隙水压力变化下的持水能力由土水特征函数来表示。非饱和土体破坏时的抗剪强度计算见第二节。整个数值分析的步骤为先采用 SEEP/W 分析渗流和地下水流，以获得边坡内接近真实的孔隙水压力分布；之后将 SEEP/W 获得的孔隙水压力分析结果导入到 SLOPE/W来进行边坡稳定性分析。

3.3 数值计算参数标定

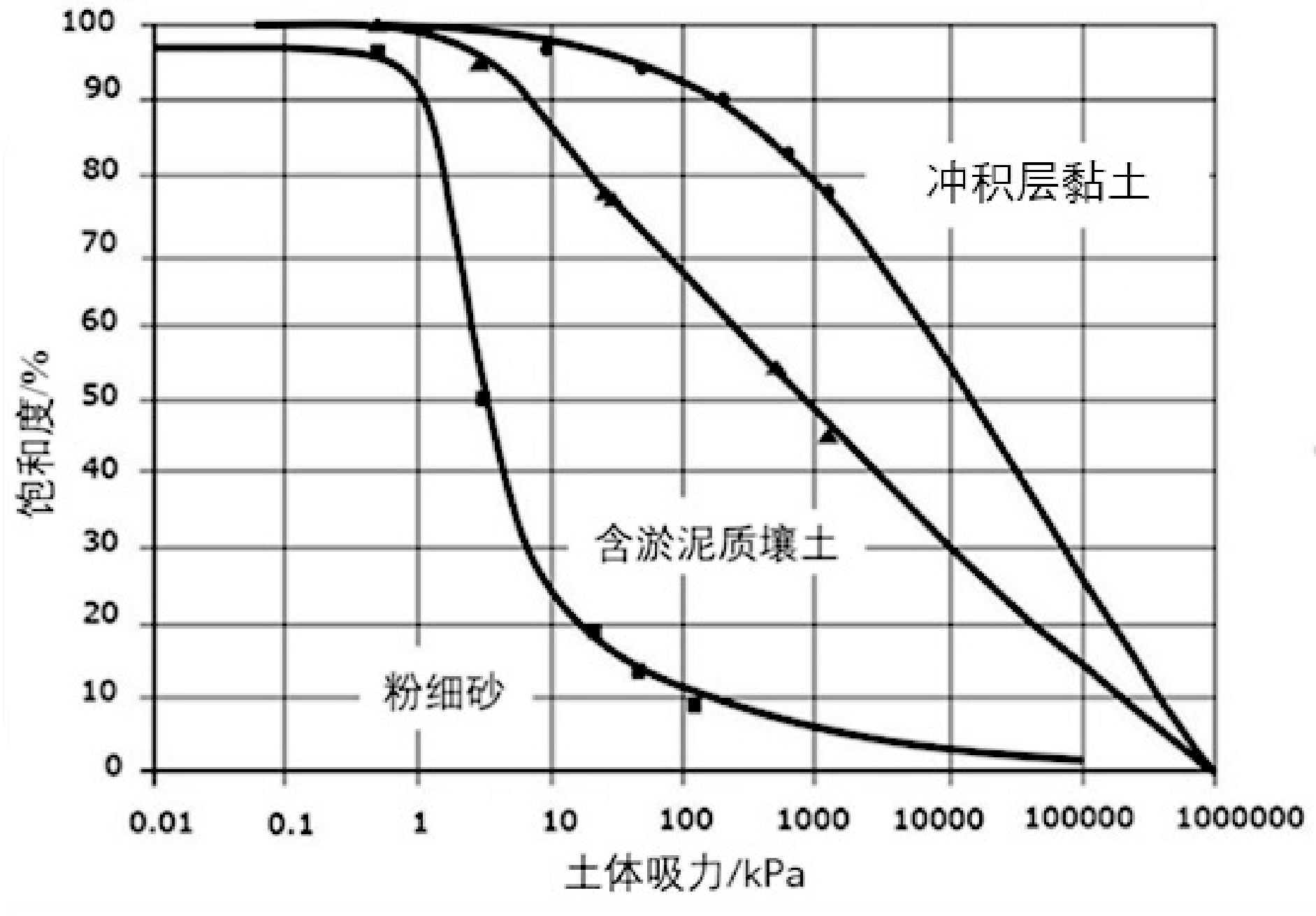
为使得数值结果计算更加精确，本文通过室内试验对 3 种土样的参数进行了标定，测试方法参考了《土工试验方法标准》（GB/T50123-2019）。图3 为一些主要参数标定仪器。由于研究的是非饱和边坡的稳定性，因此主要的试验指标包括非饱和土抗剪强度、土水特征曲线、体积含水率、渗透系数等。其中土水特征曲线是反映饱和与非饱和土之间差异的重要指标，表示在吸力不断增加的基础上土的持水能力。从图4 可以看出，土体饱和度随基质吸力增加而不断减小。由于粉细砂渗透系数大，同一吸力水平下，饱和度下降最快，其次为淤泥质壤土，而黏土的饱和度下降最慢，储水能力最好。表1为本次标定的土力学参数。

4 数值结果分析

4.1 不同坡角边坡稳定性分析

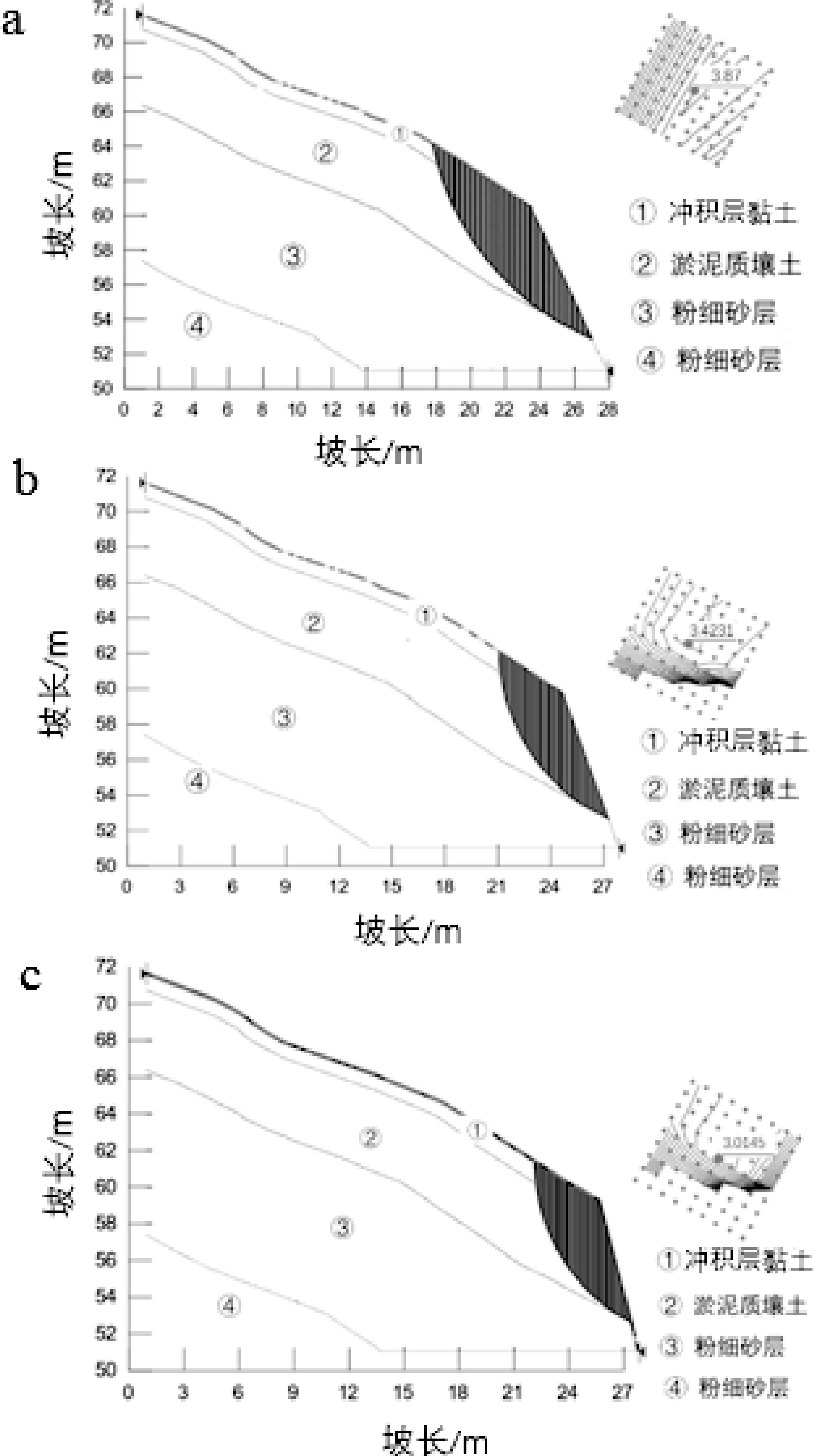
为分析边坡滑动面范围，绘制了不同开挖线下边坡的潜在滑动面（图5）。由图可知，3 种坡角下，边坡的潜在滑动面剪出口都位于泥质壤土和粉细砂层的交界面处，而坡顶的水平贯通距离明显不同。当坡角 β=65°时，潜在滑璧顶点距离零点 18.4 m；当坡角β=70°时，滑动面向右移动，潜在滑璧顶点距离零点21.2 m；而当坡角β=75°时，潜在滑璧顶点距离零点 23.9 m。因此可以得出，随着坡角增大，边坡的潜在滑动面会逐渐靠近开挖形成的临空面，即滑坡的体积会减小。此外由图中还可得出，坡角 β越大，边坡的安全系数越低，其中当坡角β=65°时，边坡的安全系数为 3.87，当 β=70°和 75°时，边坡的安全系数为3.42和3. 01，降低了11.6%和12%。

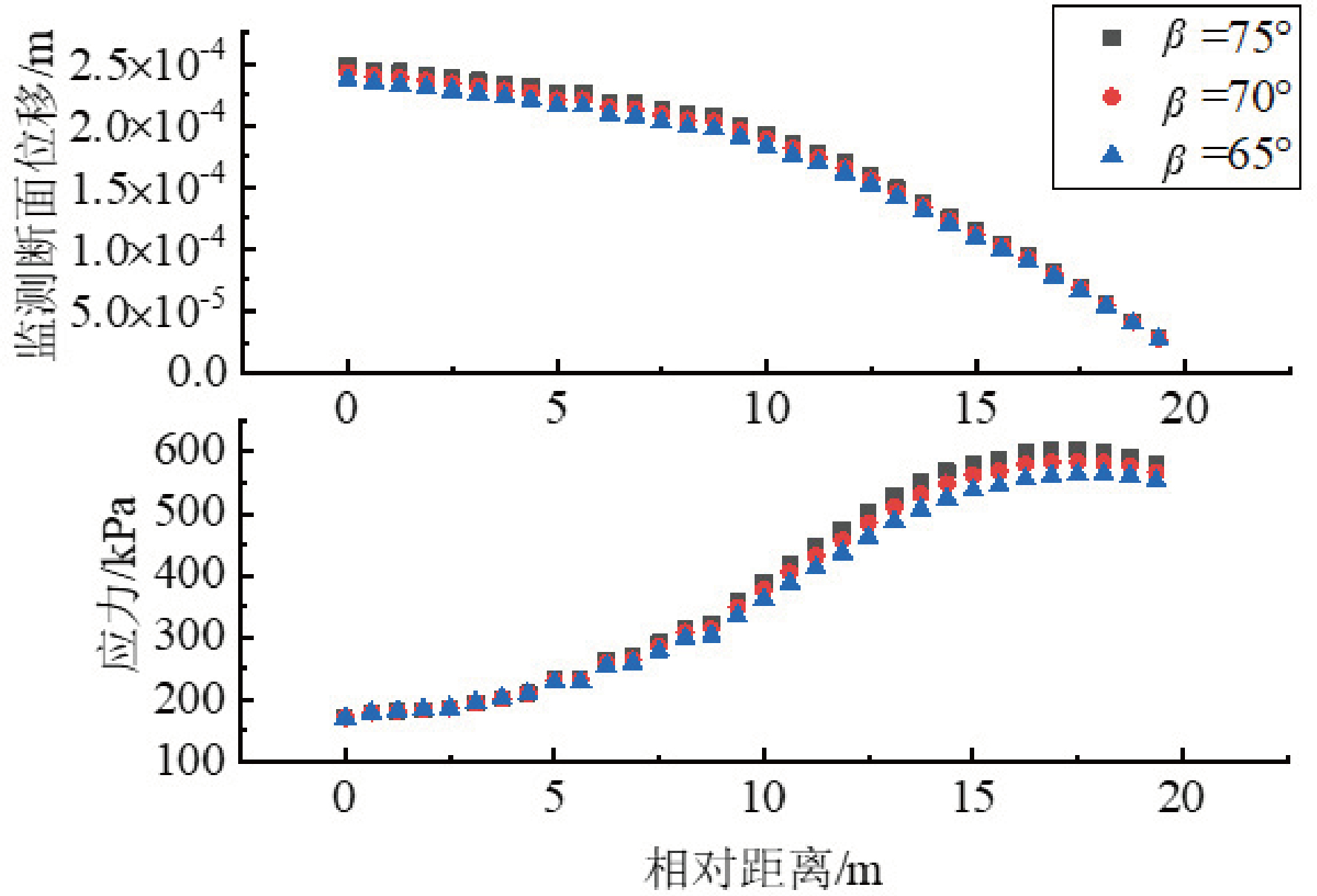
图6 给出了不同坡角下，监测断面的应力和位移随深度变化规律。由图可知，边坡深度越深，位移变化越小，说明此次放坡受影响最大的是上层的黏土和泥质壤土。此外，当深度小于 50 m 时，边坡的角度 β与监测点位移成正相关，而当深度大于 50 m时，各坡角监测点位移相差不大。此处当β=75°时的位移最大，为 0.25 mm。从图中应力随边坡深度变化的规律得出，坡体内部应力随深度增加成非线性变化规律（自重作用下呈线性变化），当深度大于 50 m 时，应力几乎保持不变，说明边坡开挖产生的卸荷区域对底层粉细砂的应力状态有影响。此外，当β=75°时的应力最大，为601 kPa。

由不同坡角下监测断面孔隙水压力随深度的变化规律图（图7）可知，随着深度增加，不同土层的孔隙水压力的数值和正负都有明显的变化。当 β= 65°时，高程为 62 m 时冲积层黏土的孔水压力为 0，之后随着深度增加，孔水压绝对值呈先增大后减小的趋势变化；当高程大于 53 m 时，粉细砂层出现正孔隙水压力，表明土的基质吸力降低。此坡角下，孔压最大值出现在淤泥质壤土层。当 β=70°，孔水压随深度变化趋势与 β=65°相似，此外二者在黏土层和粉细砂层的孔水压与深度呈线性相关，而在淤泥质壤土层呈非线性相关。孔压最大值出现在淤泥质壤土层内，高程约57 m。而当β=75°时，孔水压随深度变化趋势同样虽与前两种坡角的边坡保持一致，但孔压最大值出现在淤泥质壤土与粉细砂层交界处。本文之前得出 β=75°时边坡安全系数最小，说明在不同土层交界面处出现较大的孔隙水压力，可能会降低边坡的抗剪能力，但必须指出，根据有效应力原理，负孔隙水压力越大，毛细管吸力越大，土的抗剪强度增加。

从以上结果分析可知，不同坡角下孔隙水压力的影响区域由上层逐渐向深层土壤移动，这是由于不同坡角对边坡的潜在滑动面有一定影响，从而导致土体之间的有效应力发生变化，因此导致土体孔隙压力发生不同变化。但必须指出，孔隙水压力的变化特征与土壤的类型十分相关，因为不同土体的渗透性有明显差异，因此遇到不同土壤类型的切坡工程，其孔压会出现不同的变化规律，需要针对性进行分析。

a—β=65°；b—β=70°；c—β=75°

a—β=65°；b—β=70°；c—β=75°

4.2 不同降雨荷载下边坡安全系数变化分析

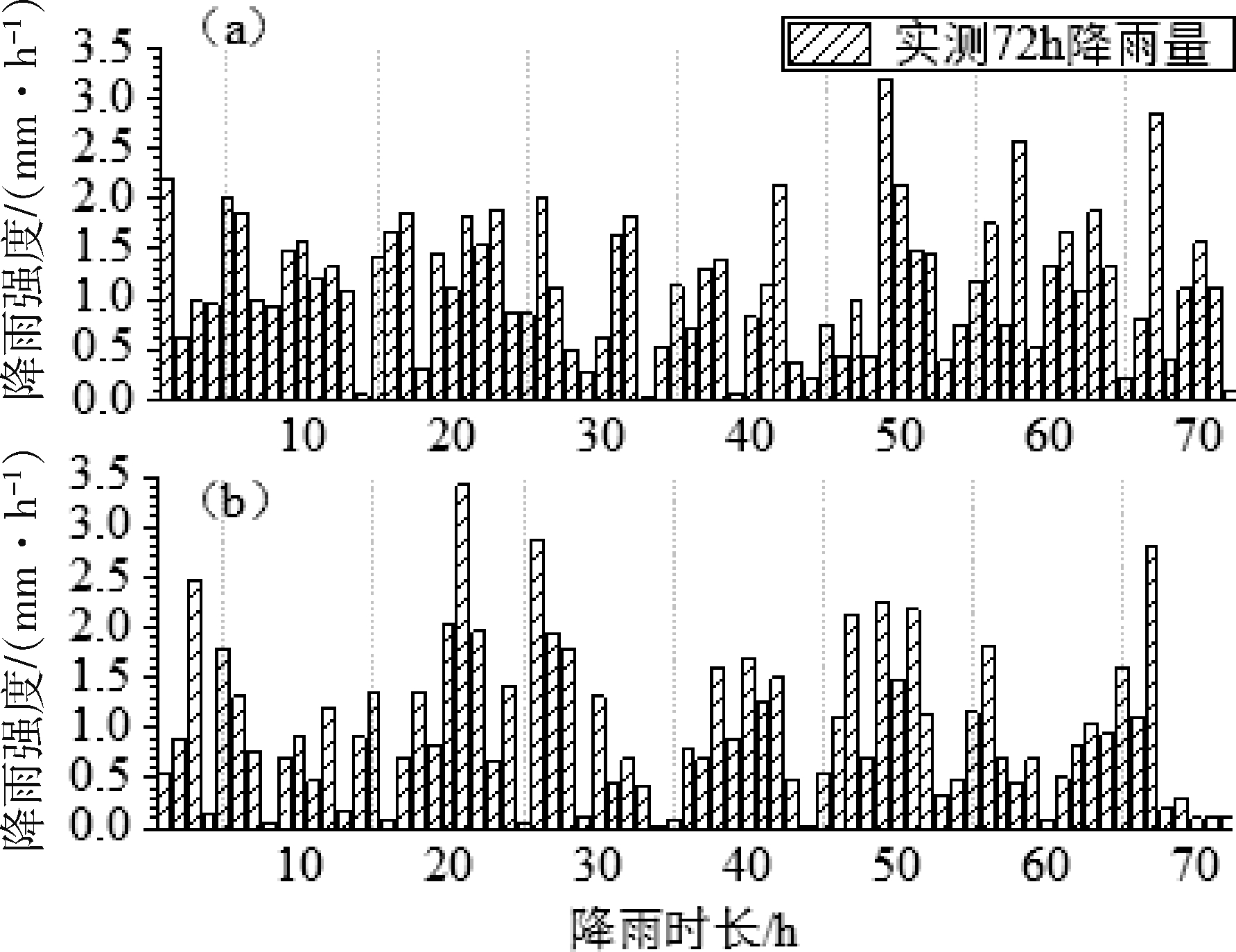
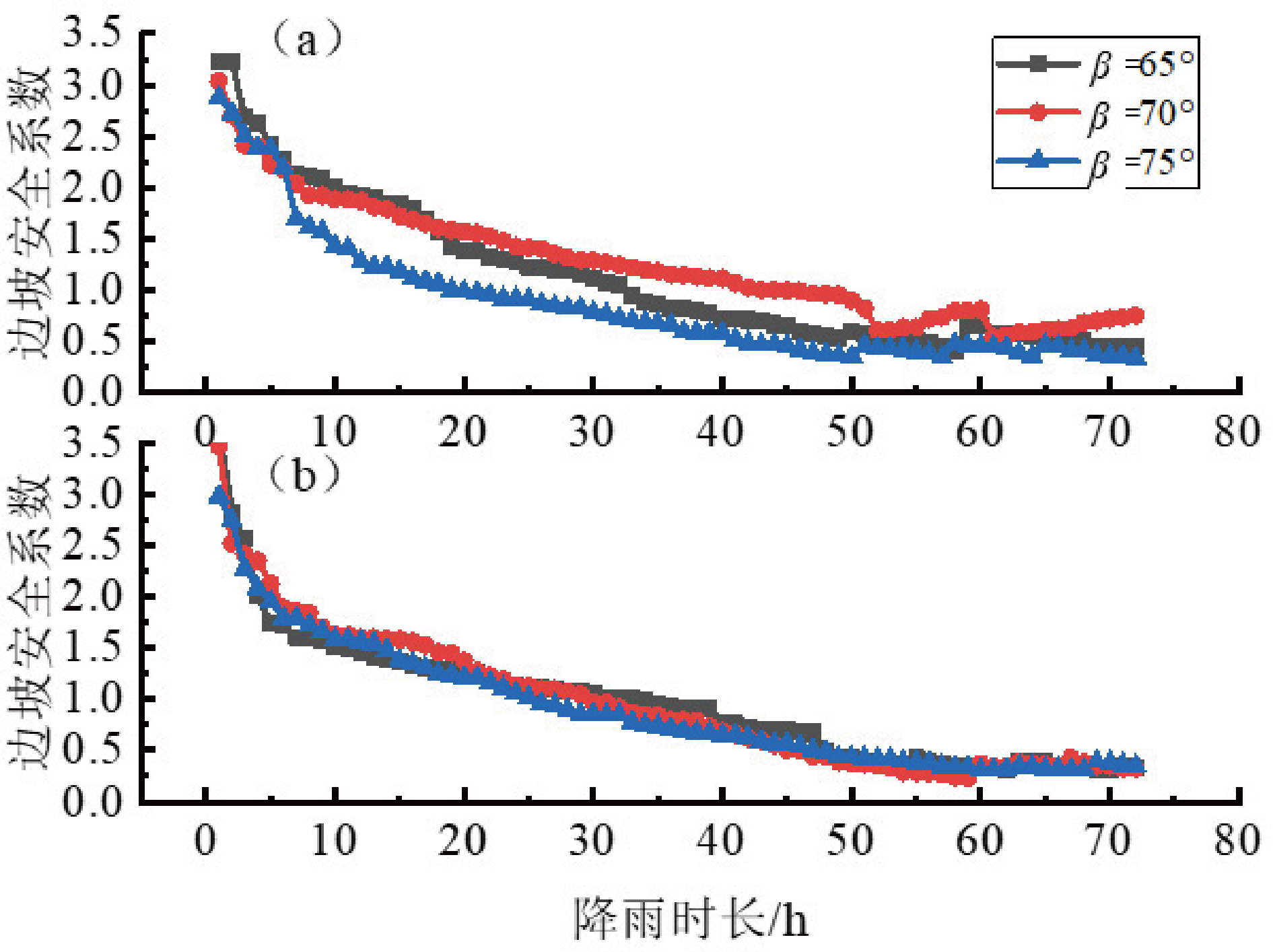
持续的降雨会升高地下水位，增加孔隙水压力，使得地下水位以上出现暂缓饱和区，同时坡内土体的总容重增加，降低了土体有效应力，从而引发滑坡。目前多数研究数值模拟中采用的降雨强度为年平均或者一时段之间的平均值，通常忽略了循环降雨荷载对边坡稳定性的影响。因此本节采用两种 72 h 实测降雨强度来评估边放坡后边坡的稳定性（图8）。图8为两种不同降雨强度下，边坡安全系数随降雨时长的变化规律。由图可知，总体上随着降雨时长增大，边坡的安全系数呈逐渐减小的趋势，但局部出现了回升的现象。当采用图8a中的降雨强度来进行模拟时，在降雨初期 β=65°的边坡安全系数最大，β=75°的边坡安全系数最小。随着降雨时长的增大，三者安全系数呈非线性降低，当降雨至 72 h后，β=70°的安全系数最大，β=75°次之； 当降雨时长为 52 h后，边坡安全系数出现了局部增长的趋势，这是由于当边坡经历密集的强降雨之后，部分浅层土层会由于渗透力而出现破坏，导致边坡安全系数急剧减小，而当降雨逐渐减小后，较深土层的孔隙水压力会成为负孔压增加土体的抗剪强度，此时残余边坡的安全系数会有回升的趋势。但必须指出，出现这一现象与土体的渗透性和结构性有较大关系，像西北黄土类陷湿性较强的土坡，随着降雨强度和时长增大，边坡安全系数会一直减小。

当采用图8b中的降雨强度来进行模拟时，可看到降雨初期边坡安全系数下降最快的是 β=75°的边坡，且由于初期有一次强降雨，三者的安全系数下降速度在整个降雨时域内都属最快，之后随着降雨时长增加，安全系数持续降低。但值得一提的是，从图8b 可以看到，当降雨峰值为 20 h 左右时，降雨强度在整个时域内达到最大，但安全系数的降速并未出现突降，这可能是由于降雨前期，边坡的安全系数已经达到了最快下降阶段，而残余土坡相对原始边坡更加稳定，因此再受较大的降雨强度时，安全系数下降减缓。此降雨强度下，边坡安全系数同样也出现了一定回升现象，但不如图8a 中的明显。从图9还得出，土质边坡在实际的降雨荷载下，具有阶段性破坏特征，因此采用某一降雨强度平均值来分析边坡稳定性并不准确，会给边坡安全施工设计带来一定误差。

a—第一种72 h降雨强度；b—第二种72 h降雨强度

a—第一种72 h降雨强度；b—第二种72 h降雨强度

4.3 不同降雨荷载下边坡孔隙水压力分析

图10 为两种降雨强度监测断面的部分降雨时长下，第二层与第三层土交界面的孔隙水压力。为节约篇幅，图中只给出了负孔压的变化情况，以观察边坡何时抗剪强度最大。由图10a 可知，当采用图8a 中的降雨强度来进行模拟时，β=65°边坡交界面处在降雨 28 h左右时，孔隙水压力处于一个平衡状态（孔隙水压力不等0），且数值不为负，说明此时段内雨水已经渗透至粉土细砂层，边坡遭受破坏。而当降雨时长为 35 h和 56 h时，负孔压数值达到最大，为-8.1 kPa。其中 β=65°边坡在图8b 的降雨强度下也呈现出同样的变化趋势，但负孔压数值达到最大时的降雨时长分别为 32 h 和 52 h。当 β=70° 时，在两种降雨强度下，孔隙水压力随降雨时长增大均呈波浪式变化，其中在第一种降雨强度下，最大负孔压出现在降雨时长为 8 h 时刻，而第二种降雨强度下的最大负孔压出现在降雨时长为 6 h 时刻，分别为-18.1 kPa 和-13.5 kPa。而当 β=75°，在两种降雨强度下，孔隙水压力随降雨时长增大近似线性增大，最小负孔压出现在降雨 5 h时刻，而第一种降雨强度下的孔压增速明显大于第二种降雨强度。

a—第一种72 h降雨强度；b—第二种72 h降雨强度

5 结论

本文采用Morgenstern-Price条分法和非饱和土抗剪切强度理论，对开挖卸荷后坡角β=65°、70°、75° 的边坡稳定性和孔隙水压力的变化规律进行了分析。最后根据两组 72 h实测降雨数值，对边坡安全系数随降雨时长变化进行了动态研究。结果表明：

（1）随着坡角增大，边坡的潜在滑动面会逐渐靠近开挖形成的临空面，即滑坡的体积会减小。坡角β越大，边坡的安全系数越低；

（2）随着深度增加，不同土层的孔隙水压力的数值和正负都有明显的变化；

（3）边坡经历降雨过后，其安全系数总体上会随着降雨的进行逐渐减小，但会随着降雨强度的变化出现小幅波动。

由以上结果可知，坡角对边坡稳定性有较大影响，在进行实际切坡工程时，应当尽量降低坡角来保持边坡稳定性，对于需要留取较陡边坡的工程，应采取相应的加固措施来防止边坡出现滑坡等灾害。同时，采用实际降雨数据对边坡稳定性分析能够真实反映边坡安全系数边坡变化，对边坡稳定性设计具有实际意义。本文的研究方法对常见的黏土和砂土等边坡具有一定适用性，而对于膨胀土和黄土等结构特殊边坡需要进一步采用新的本构关系进行研究。

参考文献