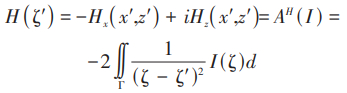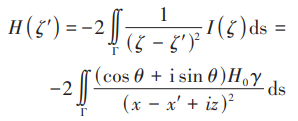-
0 引言
-
磁法勘探是寻找铁磁性矿体或岩体的一种有效方法(苏士星等,2022;周豪等,2024),传统的数据解释以定性方法为主,如化极、延拓、边界识别等,后来发展了二维、三维人机互动拟合反演、自动反演等众多基于位场的反演算法。Tarantola and Valette(1982)利用阻尼最小二乘方法解广义的非线性反演问题,从而得到稳定解的方法。刘天佑和管志宁(1986)采用广义逆矩阵的选择法迭代反演二维磁异常,能够较准确的得到有限个组合板状模型。随着计算机技术发展,出现更多新的算法。如三维平滑正则化反演(Li,2001)、三维聚焦反演 (Zhdanov et al.,2004)、聚类-c 均值聚焦反演方法 (Sun and Li,2015)、基于线性相关约束的联合反演方法(Oldenburg and Li,1999)、以及许多三维位场梯度反演方法(Zhdanov,2009b;Zhdanov et al., 2012,Zhdanov and Lin,2017;Oliveira and Barbosa, 2013;高秀鹤和黄大年,2017),以上三维反演是复杂的、耗时的,因为它取决于先验模型和约束条件。
-
偏移成像是一种高效率的数据处理方法,在地震波场成像(Kunetz,1972; Schneider, 1978; Berkhout,1980; Claerbout,1985)和电磁场成像 (Zhdanov and Booker,1993;Zhdanov,2002,2009a) 中发展较早。从数学上讲,偏移是由伴随算子对观测数据的作用来描述的,其中伴随算子表现为地震或电磁场的反向传播函数。势场中偏移成像的概念由 Zhdanov(2002)首先引入的,其本质是通过向下解析延拓确定场源位置,其偏移表现为势场及其梯度向下延续的一种特殊形式。但是,向下延拓的数理方程属于不适定问题,其方程解不稳定,容易发散。为了克服这个问题,假设以观测平面为镜面在上半空间存在一个虚拟的“镜像场源”,与其对应的势场称为“镜像场”,数学上称为“偏移场”,对该 “偏移场”做向下延拓,意味着其远离“镜像场源”,此偏移过程实际上为向上延拓,由于向上延拓的数理方程满足狄里希莱第一边值问题,其方程解是收敛且稳定的,因此,此假设正确可行的。偏移场(镜像场)可通过偏移算子由实测场转化而来。
-
伴随算子可以进行多次迭代,从而使迭代势场偏移等价于正则化反演过程,与电磁偏移迭代类似 (Zhdanov,2009a)。田明阳等(2018)基于位场偏移成像原理实现二维重力及其梯度的偏移成像 (Zhdanov et al.,2012)。
-
本文在前人研究的基础上,基于势场偏移思想,开展了数值模拟和物理试验偏移成像算法研究,构建多个模型算例验证二维磁场及其梯度偏移成像的效果,对网格剖分做了优化,设置不同噪声数据测试程序算法的稳健性。通过物理试验获得实测磁场数据,测试算法实际应用的可行性。
-
1 磁场及其梯度正演模拟
-
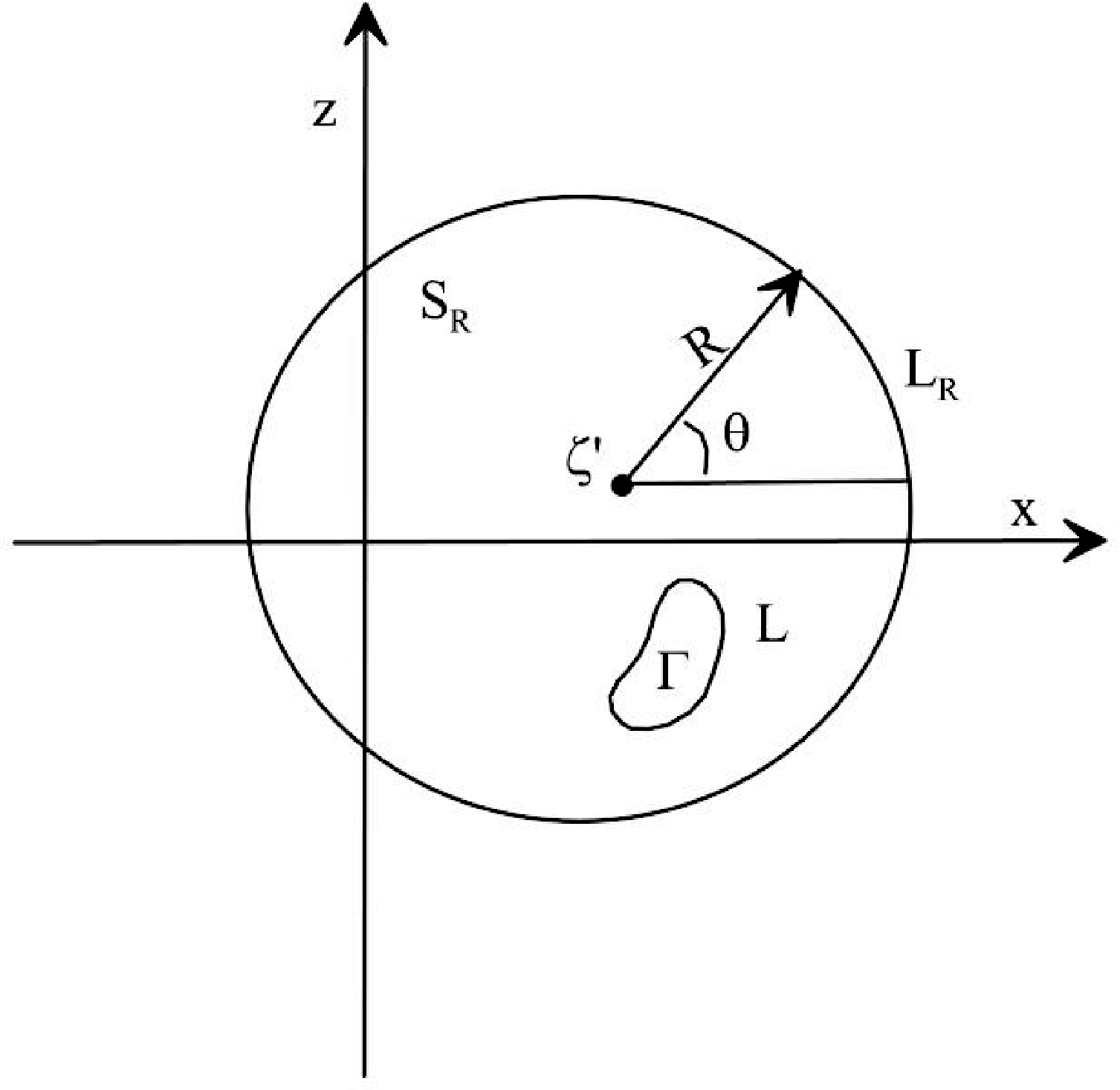
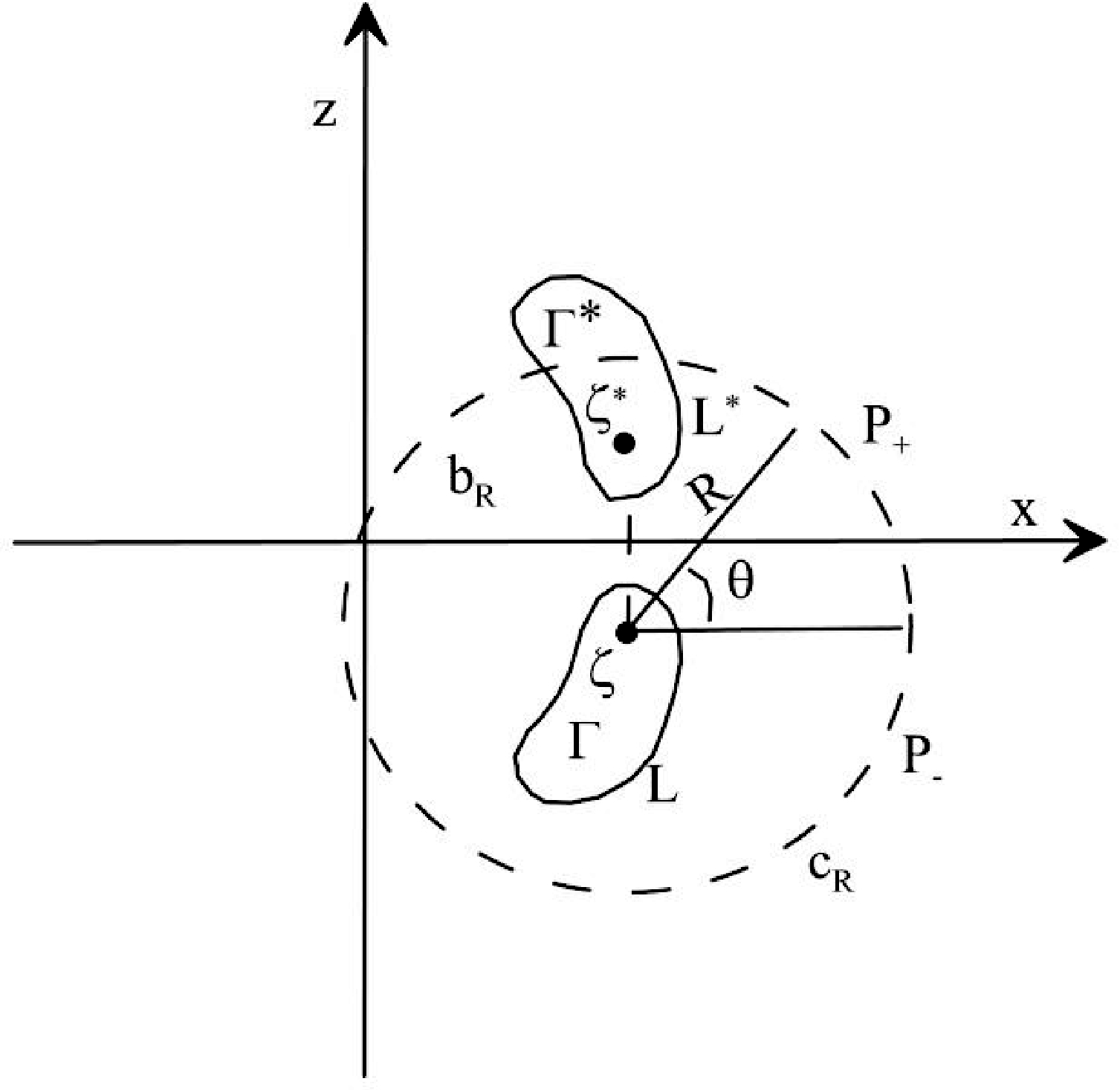
基于 Zhdanov et al.(2012)提出的磁化强度复数形式(图1)满足下面公式
-
式(1)中:ζ = x + iz
-
则磁场强度在复平面内这样定义:
-
式(2)中,AH 为正演算子,ζ‘ = x' + iz'Ix( x,z)=H0γ( x,z)cos θ;
-
设定测线在地面 z' = 0,将式(3)代入到式(2) 中,则在测线上的磁场强度满足:
-
对于磁场梯度 ,可得到下面公式:
-
式(3)~(5)中 ζ 是磁性体上任意一点:ζ = x + iz,ζ`是空间任意一点,ζ' = x' + iz'。设 γ 为磁化率, H0为地磁场强度。
-
图1 二维磁问题假设复平面
-
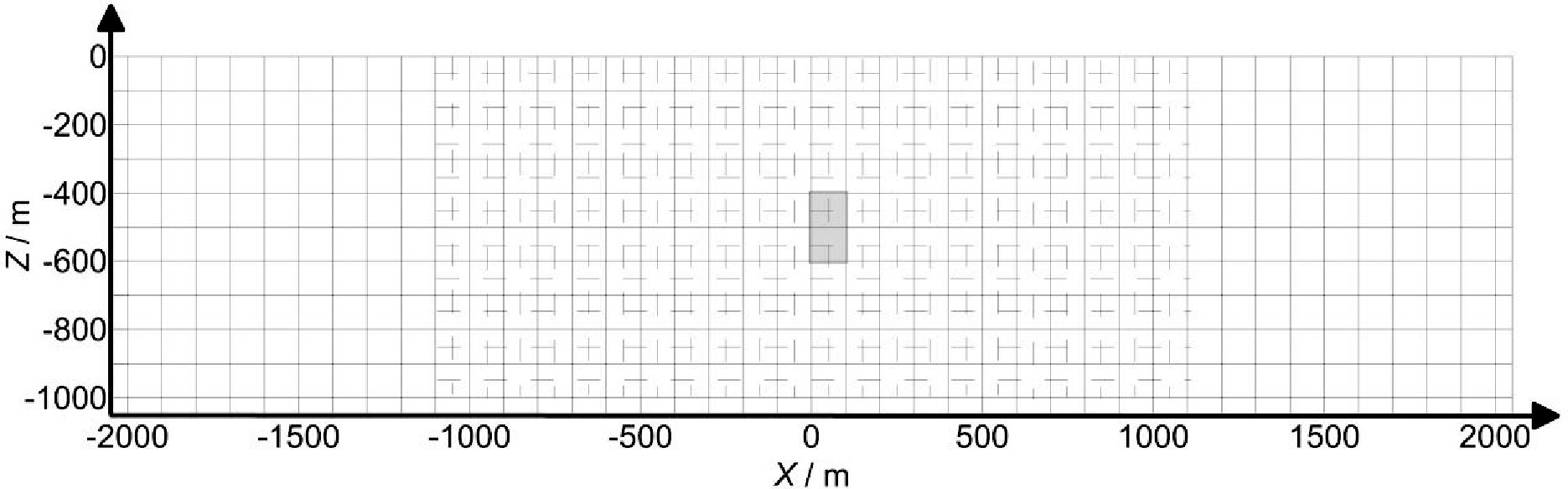
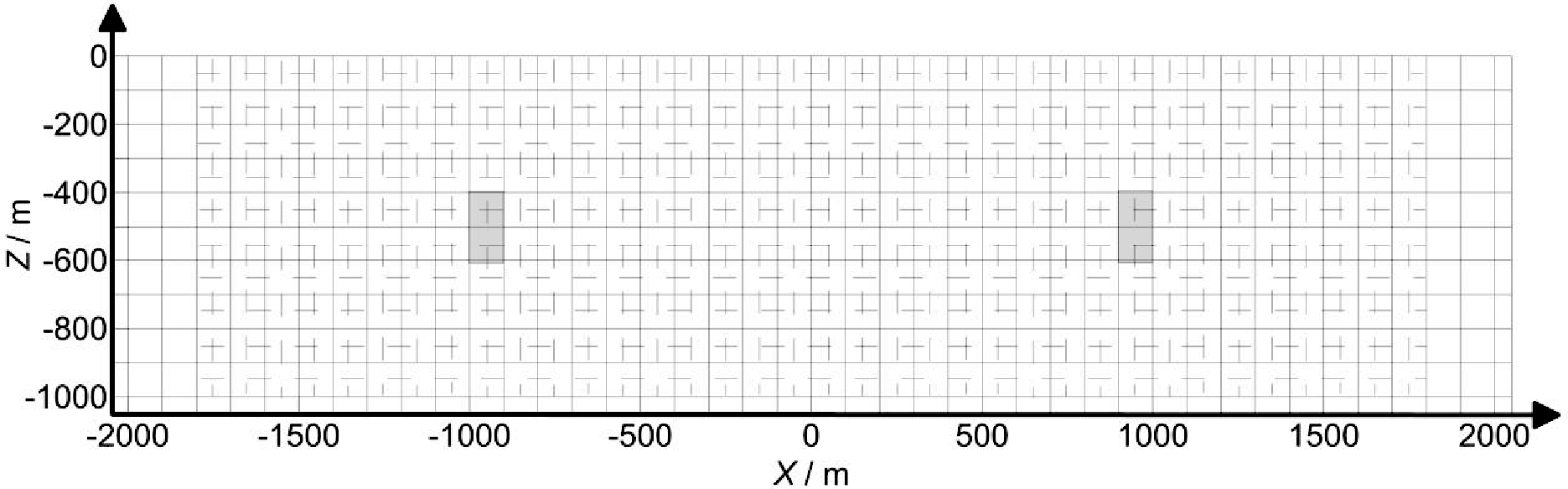
据式(4)和(5),编写程序计算二维磁场分布。为了使公式中分母不为零,剖分地下网格时采用双网格方式,即分为背景场网格和模型网格。建立模型一:图2中实线网格是背景场网格,计算区域 x方向-2050~+2050 m,步长 100 m,z 方向-50~-1050 m,步长 100 m。虚线是模型网格,模型区域 x 方向-1100~+1100 m,步长 100 m,z 方向 0~-1000 m,步长 100 m,其中灰色填充的网格表示磁性体的位置及大小,该磁性体沿 x 方向长 100 m,沿深度方向长 200 m,顶埋深-400 m,中心位于 x=50 m 处,磁化率为0.4 SI,其他单元磁化率为0 SI。计算磁性体在地面(Z=0)处产生的总磁场的水平分量 Hx,垂向分量Hz,和其梯度场Hzz与Hzx。
-
图2 背景场网格与模型网格(模型一)
-
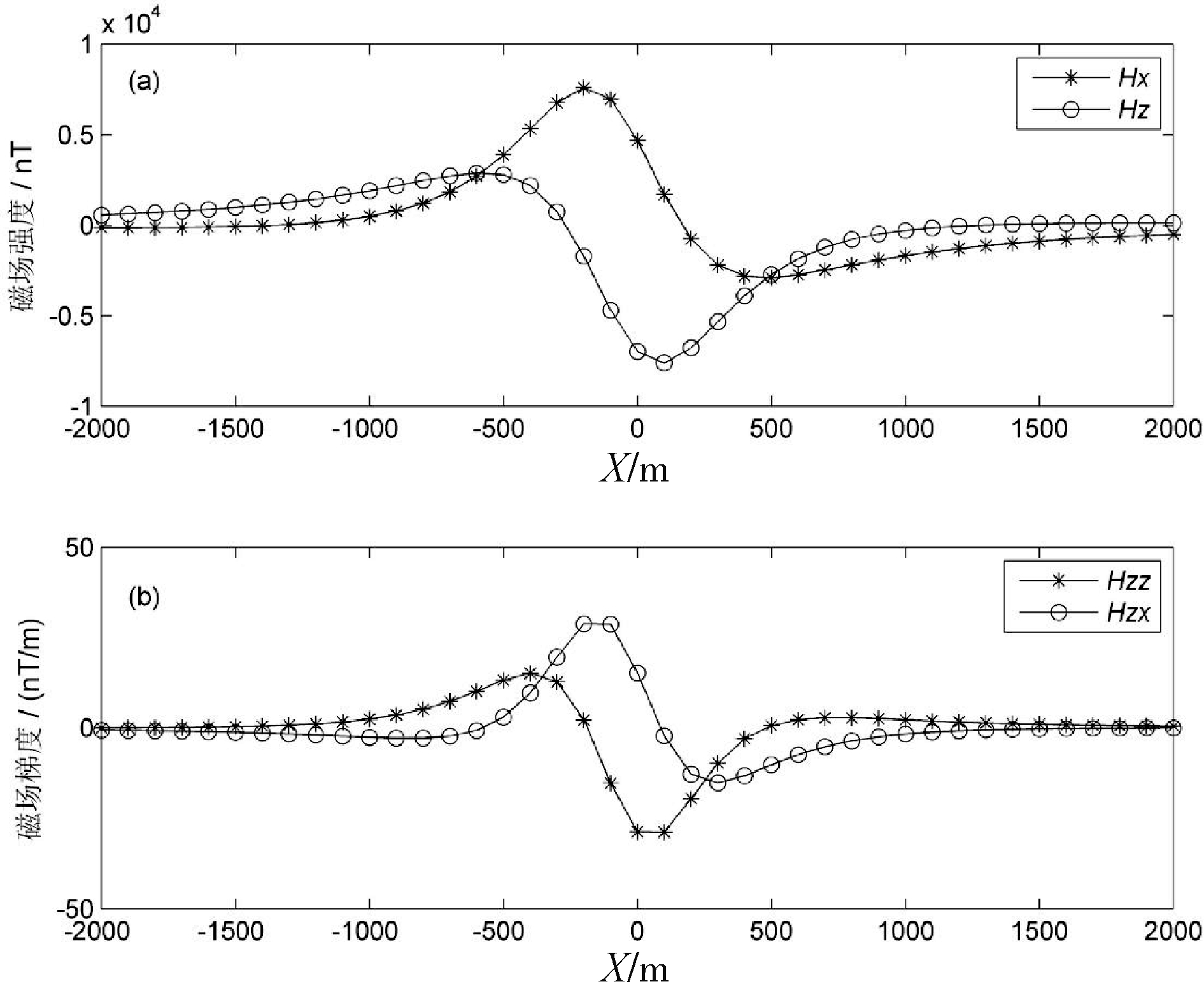
图3 是正演计算结果,磁场强度垂直和水平分量异常部位主要分布在-550~+450 m,而磁场梯度的异常集中在-500~+400 m,从正演结果来看,磁场梯度异常范围更窄,接近于磁性体的水平位置。将模型二与模型一的正演结果对比,随着磁性体顶埋深加大,磁异常幅值变小、横向范围变宽,意味着确定磁性体位置的难度变大。
-
图3 模型一在地表正演磁场(a)及其梯度(b)
-
2 磁异常偏移成像原理
-
讨论磁场偏移成像问题,需要引入几个概念,即伴随算子、伴随场以及偏移成像方法,基于前面讨论的磁场正演算法,通过建立希尔伯特空间复平面(图4),可以推导出磁场强度的伴随算子为:
-
其中,H*Γ( x')是镜像磁场强度。
-
由于 Γ* 是位于下半空间磁性体 Γ 的镜像, H*Γ( x')是由 Γ* 引起的镜像场。经过推导可得到磁场的伴随场 HΓ*(ζ)与伴随算子 AH⋆(HΓ)之间的关系为
-
设磁场强度的积分灵敏度为 SH,深度加权函数为wH,有以下关系:
-
图4 定义伴随场(据Zhdanov et al.,2011)
-
经过推导,得到磁化率分布满足下面公式
-
其中:
-
将式(10)和(11)展开将得到磁化率分布函数为
-
以同样的推导方式可以得到磁场梯度的偏移成像公式如下:
-
其中 Hzz 和 Hzx 分别为垂直磁场 Hz 沿 z 方向梯度和沿x方向梯度。
-
3 偏移成像算例测试
-
3.1 理论模型正演数据测试
-
模型二如图5 所示:两个磁性体顶埋深均为 400 m,水平距离为 1800 m,磁化率均为 0.4 SI,沿 x 方向长为 100 m,沿深度方向长约 200 m,左边磁性体中心位于x=-950 m处,右边的磁性体中心位于x= +950 m处。
-
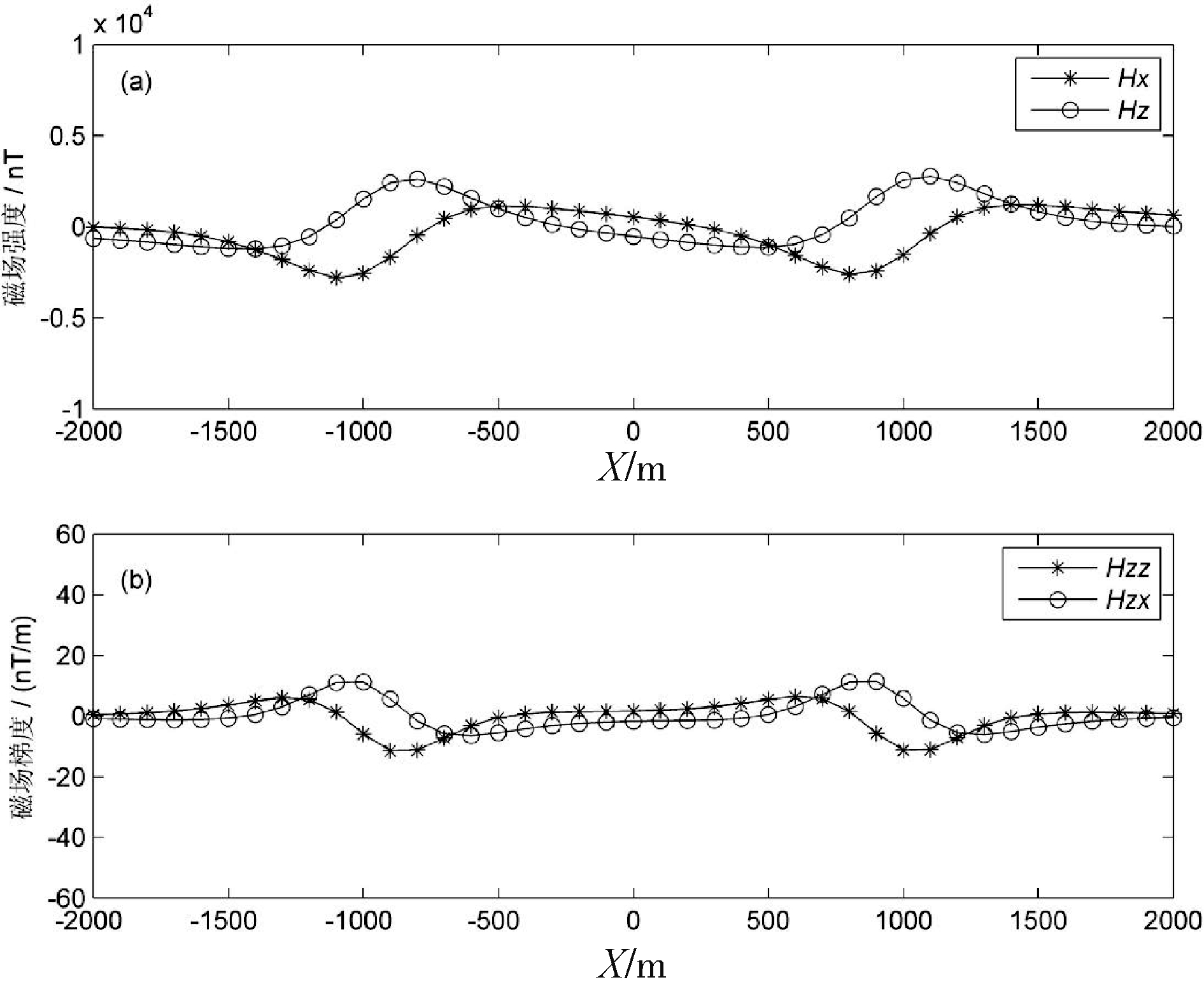
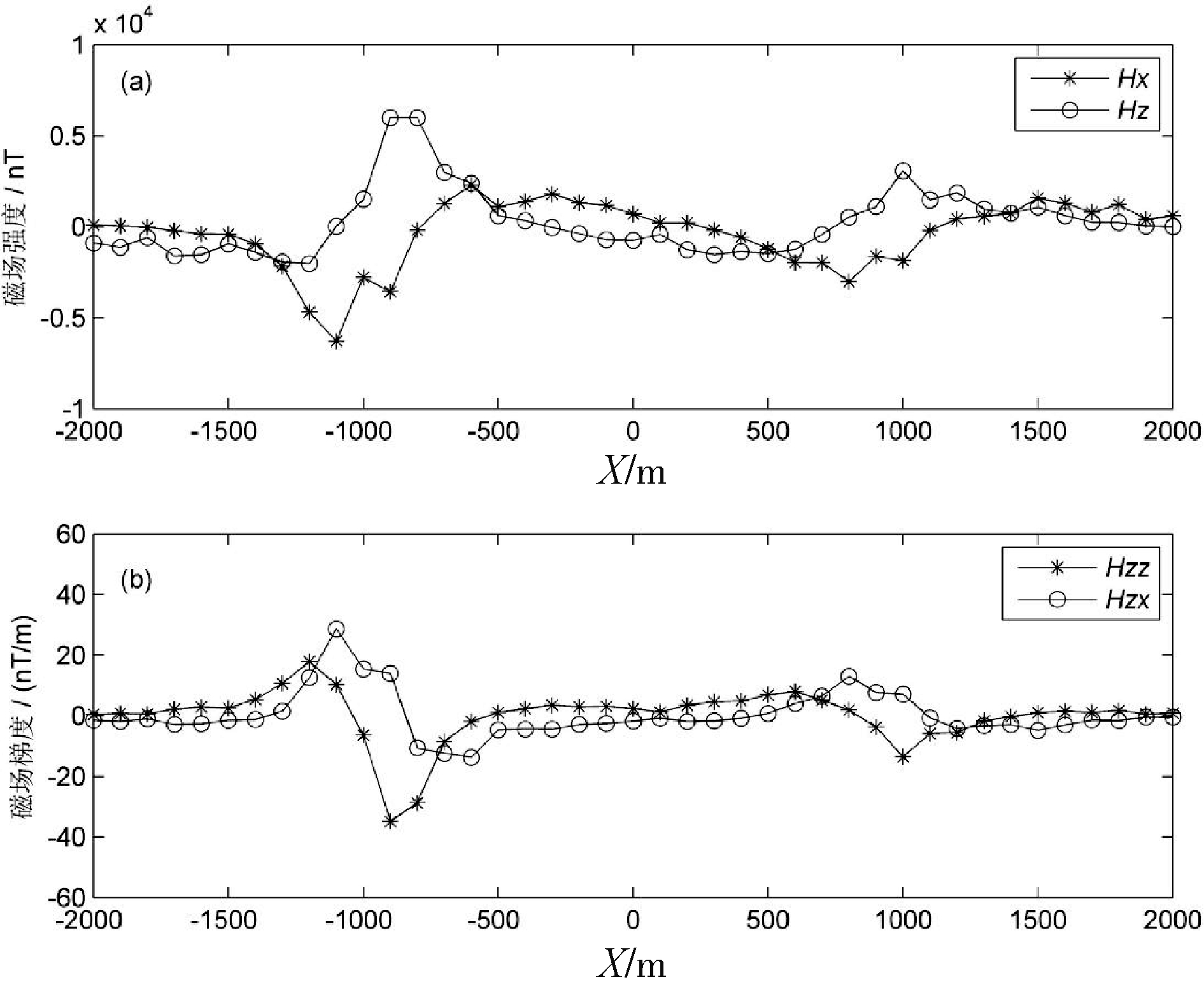
经过正演计算,获得垂直和水平磁场分量值 (图6a),以及垂直和水平磁场分量的梯度值(图6b)。可以看出,尽管两个磁性体相距较远,磁场两个分量还是受到一定的影响,比如Hz异常对称性不好,Hx异常极小值要大于极大值。
-
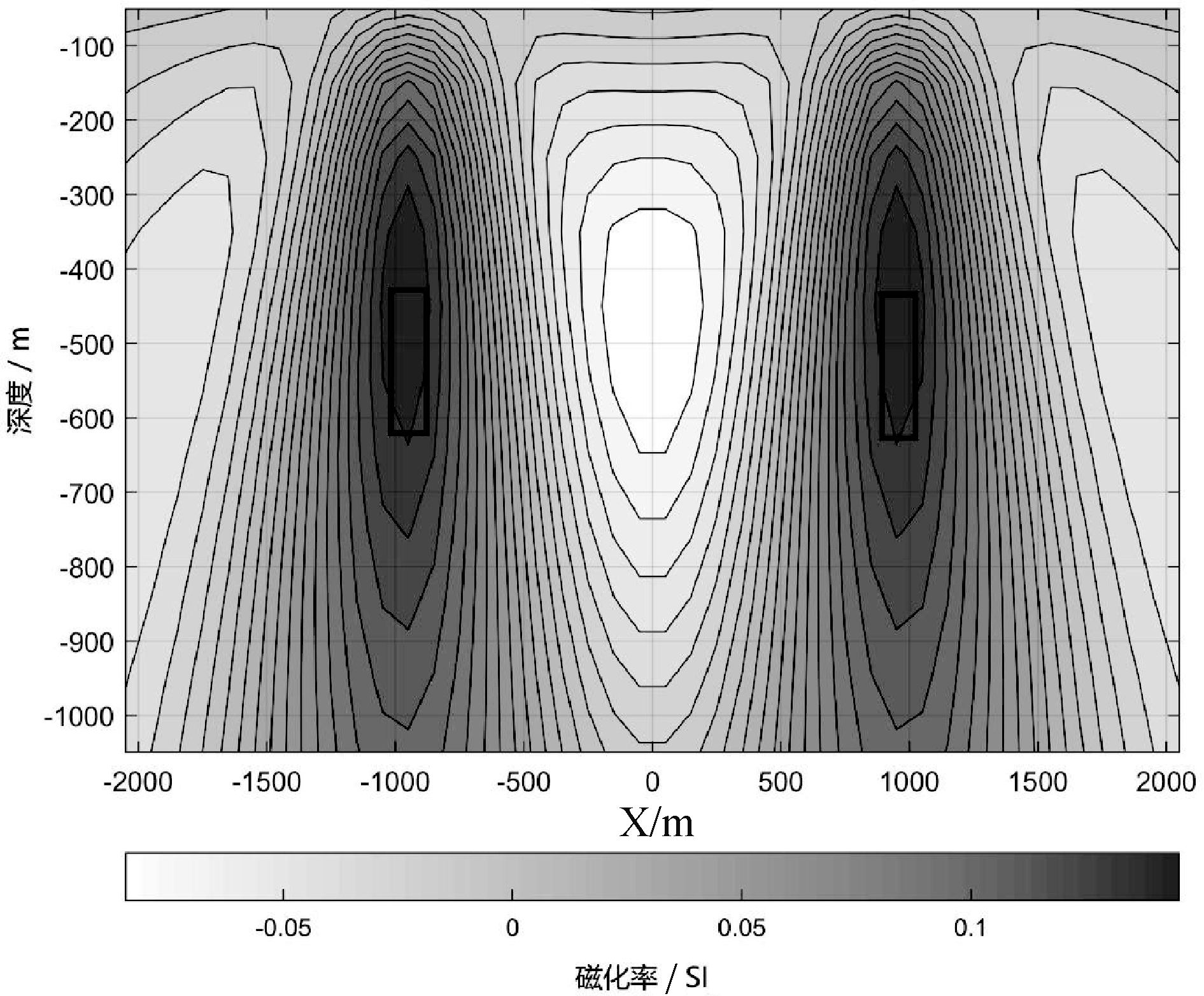
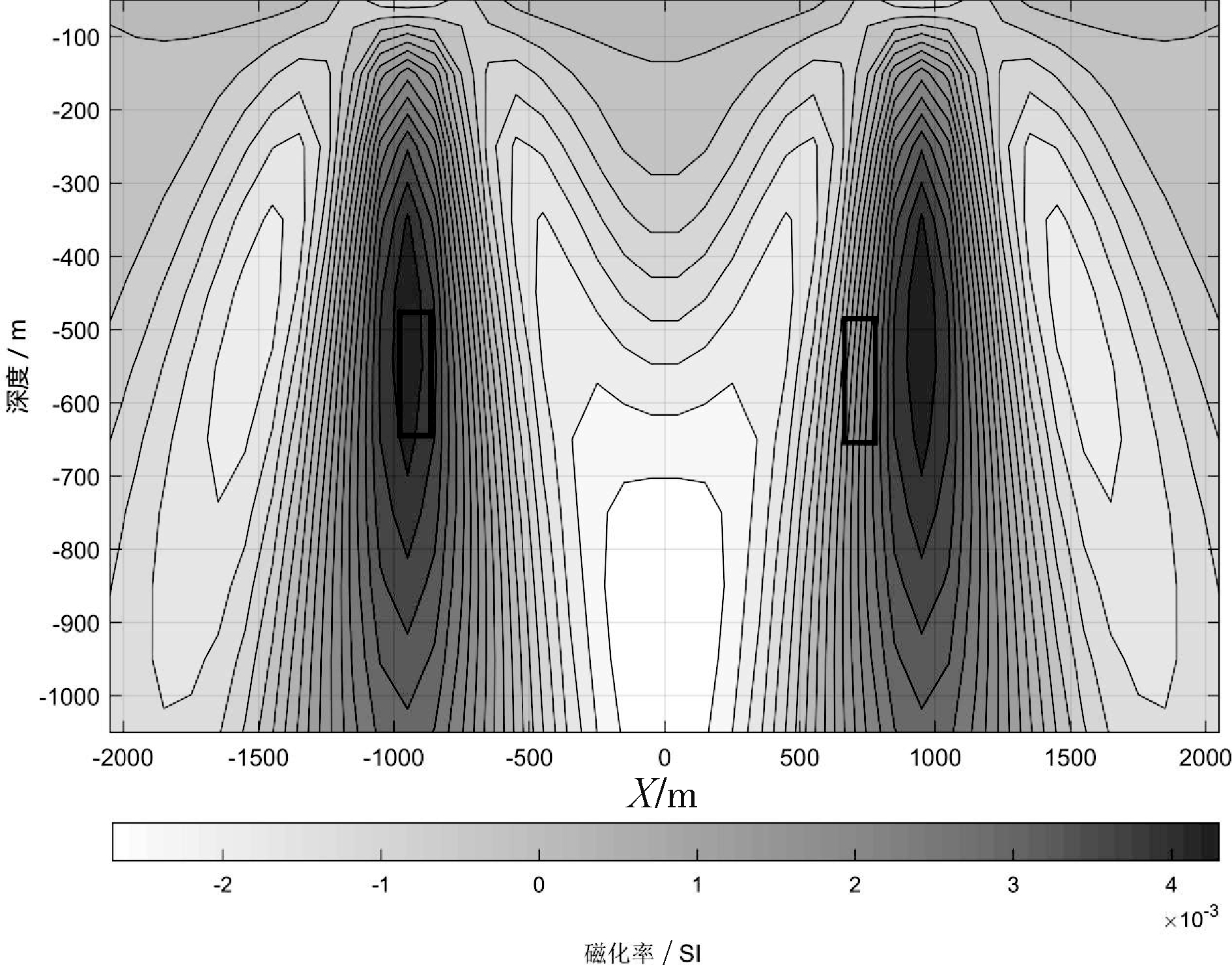
对上述磁场分量数据进行偏移成像,结果如图7和图8所示。在磁场偏移成像中(图7),获得地下单元磁化率最大值为 0.15 SI,较小于模型理论值 0.4 SI,其两个磁性体中心位置与模型中磁性体中心位置吻合;磁场梯度偏移成像(图8)对应磁性体的位置较为准确,单元磁性体的磁化率最大值为 0.1 SI,与模型磁性体位置吻合,但磁化率偏小。同时也可以观察到磁场梯度的反演结果比磁场的反演结果收敛性更好一些。
-
图5 两个相同埋深的磁性体(模型二)
-
3.2 噪声对偏移算法稳定性影响测试
-
模型三:在模型二的基础上,将左边磁性体的顶埋深调为-300 m,其他参数不变。
-
图6 模型二上方正演模拟磁场及其梯度
-
图7 磁场分量偏移成像(模型二)
-
图8 磁场梯度偏移成像(模型二)
-
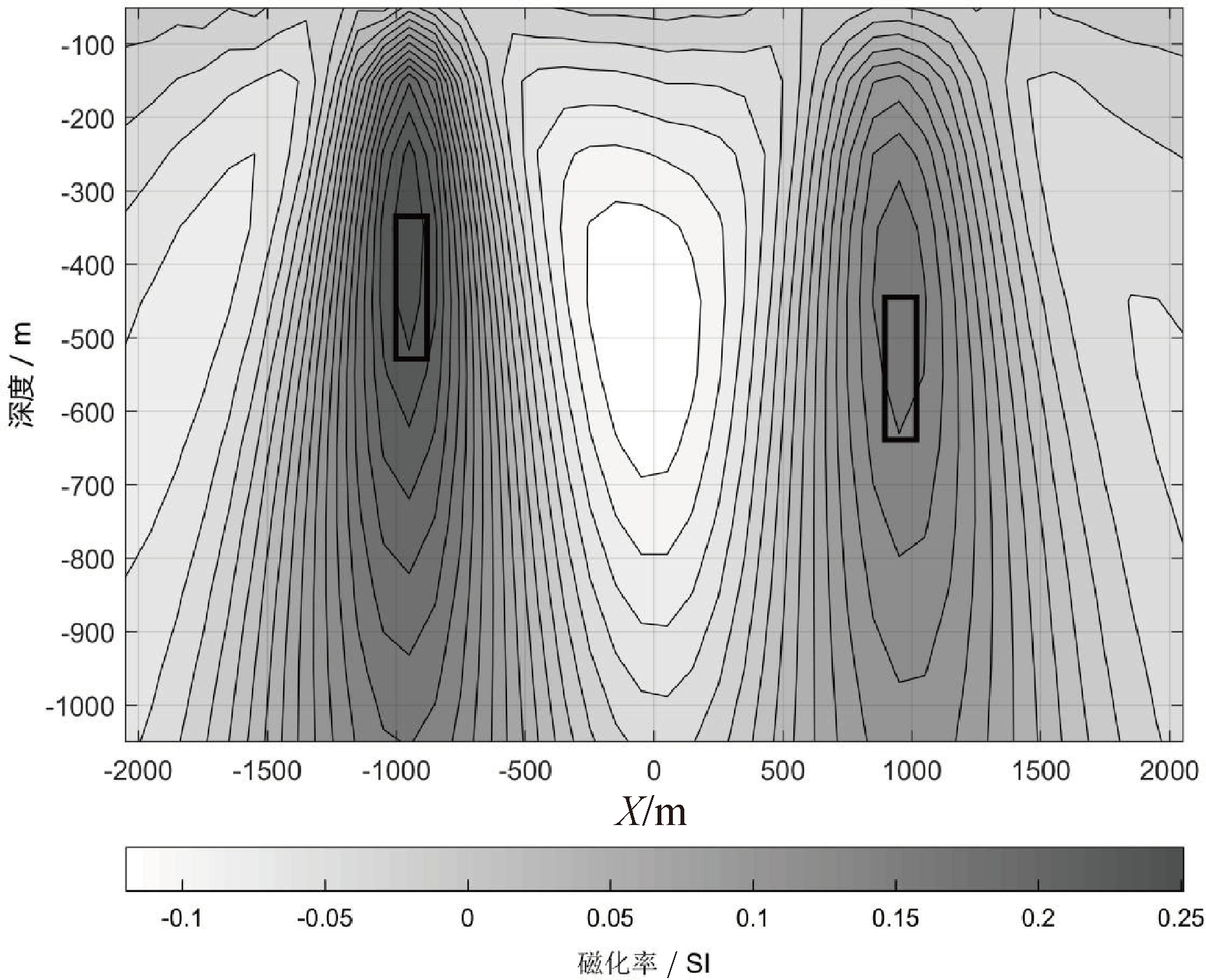
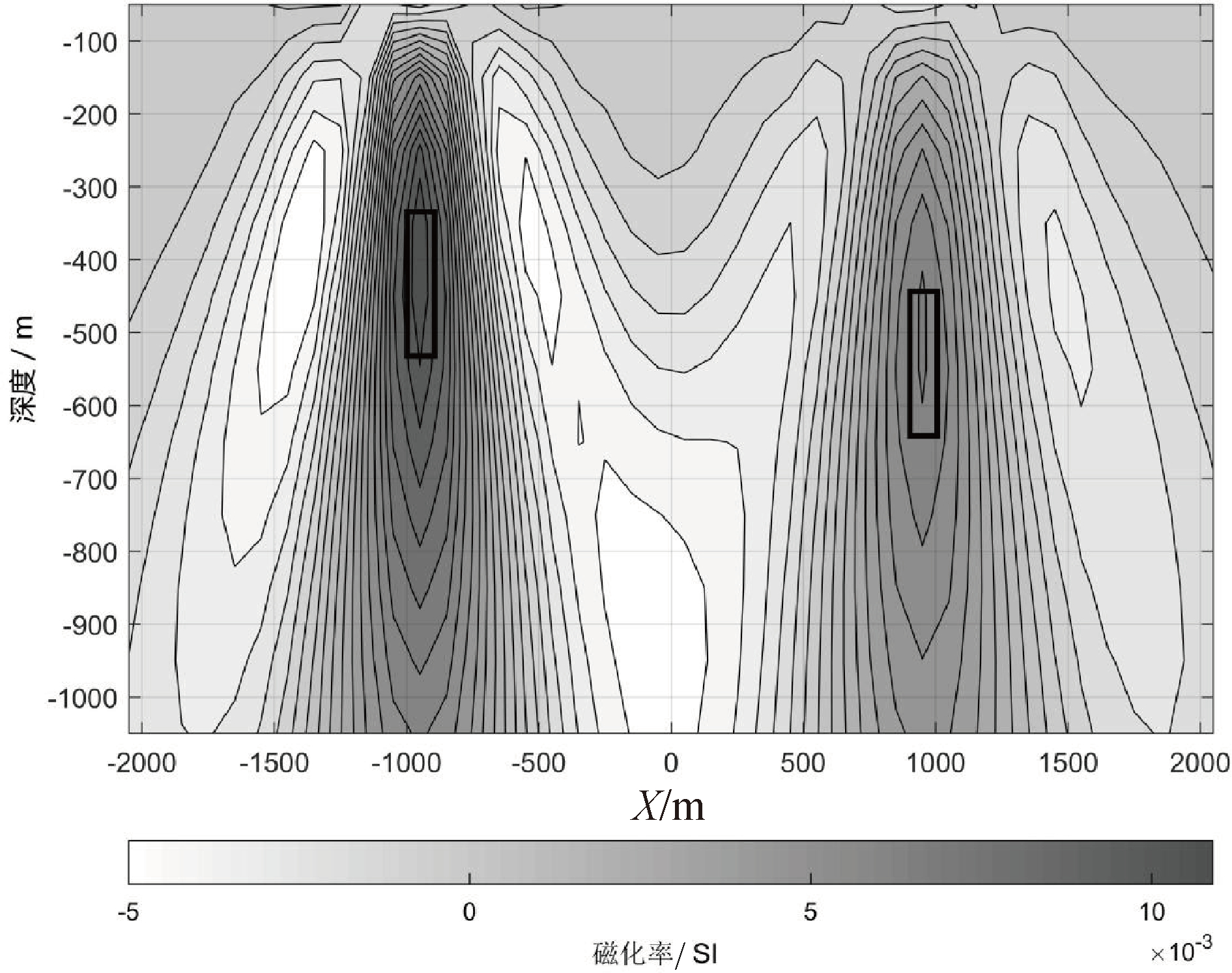
为了检验算法抗干扰能力,需要构建一组含有噪声的数据,具体做法是将模型三正演计算的理论磁场值乘以 0.5,再乘以白噪声函数(在 0~1之间变化的随机数),再加上正演计算的理论磁场值,由图9 可看出,4 条正演磁场值曲线波动变大,最大变化值能够达到理论磁场值的一半(即 50%),说明施加的干扰足够大。以此数据为原始数据,进行偏移成像,结果如图10和图11所示,两个磁化率等值线中心与模型磁性体的位置吻合较好,左边顶埋深为-300 m的磁性体位置反映更好,右边顶埋深为-400 m的磁性体成像重心偏上一点,这是由于埋深增大,分辨率降低的原因。由此可见,偏移成像算法具有稳健的抗干扰能力,即使施加50%的噪声数据也能稳定收敛。
-
图9 增加50%噪音后磁场及梯度正演曲线(模型三)
-
图10 模型增加50%噪音的磁场分量偏移图像(模型三)
-
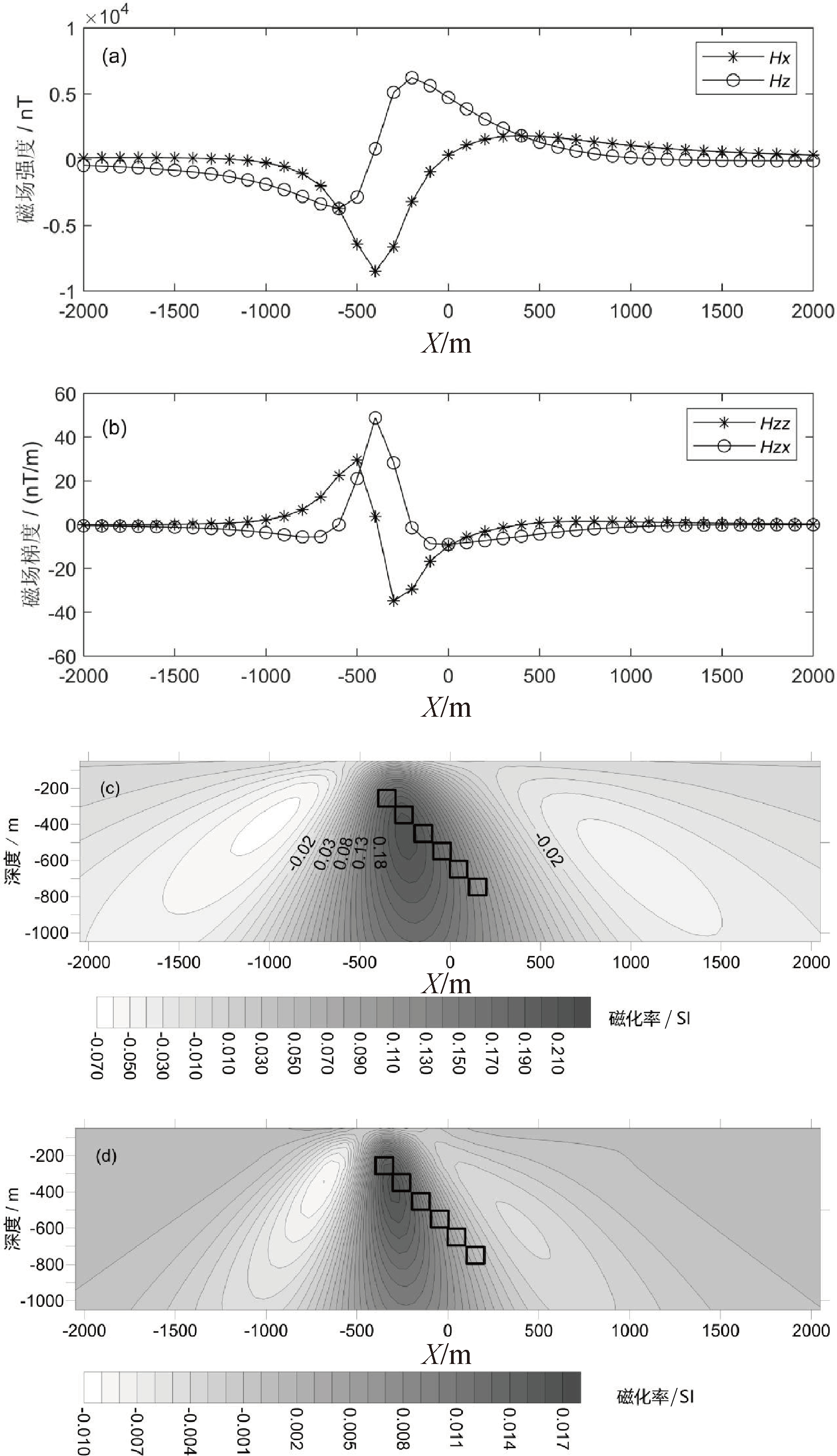
为了测试该套算法对复杂模型的正反演能力,本文制作了一个倾斜模型(模型四),由 6 个边长为 100 m的正方形异常体沿右下约45°方向延伸组成,顶埋深 200 m,异常体磁化率等于 0.3 SI,围岩磁化率为 0 SI,背景地磁场 48000 nT,45°斜磁化。通过正演获得其x和z方向的磁场分量(图12a)和磁场分量梯度(图12b),分别对上述正演数据进行偏移成像,其结果为图12c和图12d。在采用磁场分量进行偏移成像中,磁化率异常总体反映了磁性体的位置,特别是上部吻合较好,中下部成像的倾斜度较陡,意味着对深部分辨率较低。两边的负值不对称,倾向方向负值较小,倾向反方向负值较低,由此也可以判断磁性体是倾斜的。
-
图11 模型3增加50%噪音后磁场梯度偏移图像
-
在磁场分量梯度的偏移成像中,由于聚焦算法,可以更清楚地看到成像区域比较集中,横向分辨率明显比磁场分量成像要高一些,中间高磁化率区域向右倾斜,两侧负异常也不对称,其特点与磁场分量成像一样。
-
倾斜磁性体正反演结果表明,该套偏移成像算法对复杂倾斜模型也有较好的成像能力。
-
3.3 物理试验数据测试
-
为了进一步检验偏移成像算法对实测数据的适应性,在室外用磁力仪对一个铁块(5 cm ×5 cm × 5 cm)进行实际观测(图13),测线为东西方向,长 3. 0 m,点距 0.1m,距离地面 0.3 m,探头间距 0.6 m,磁场梯度值规定为探头1减去探头2。当观测水平梯度 Hxx时如图13 左边两个探头水平放置,当观测垂直梯度Hzx时如图13右边两个探头垂直放置。
-
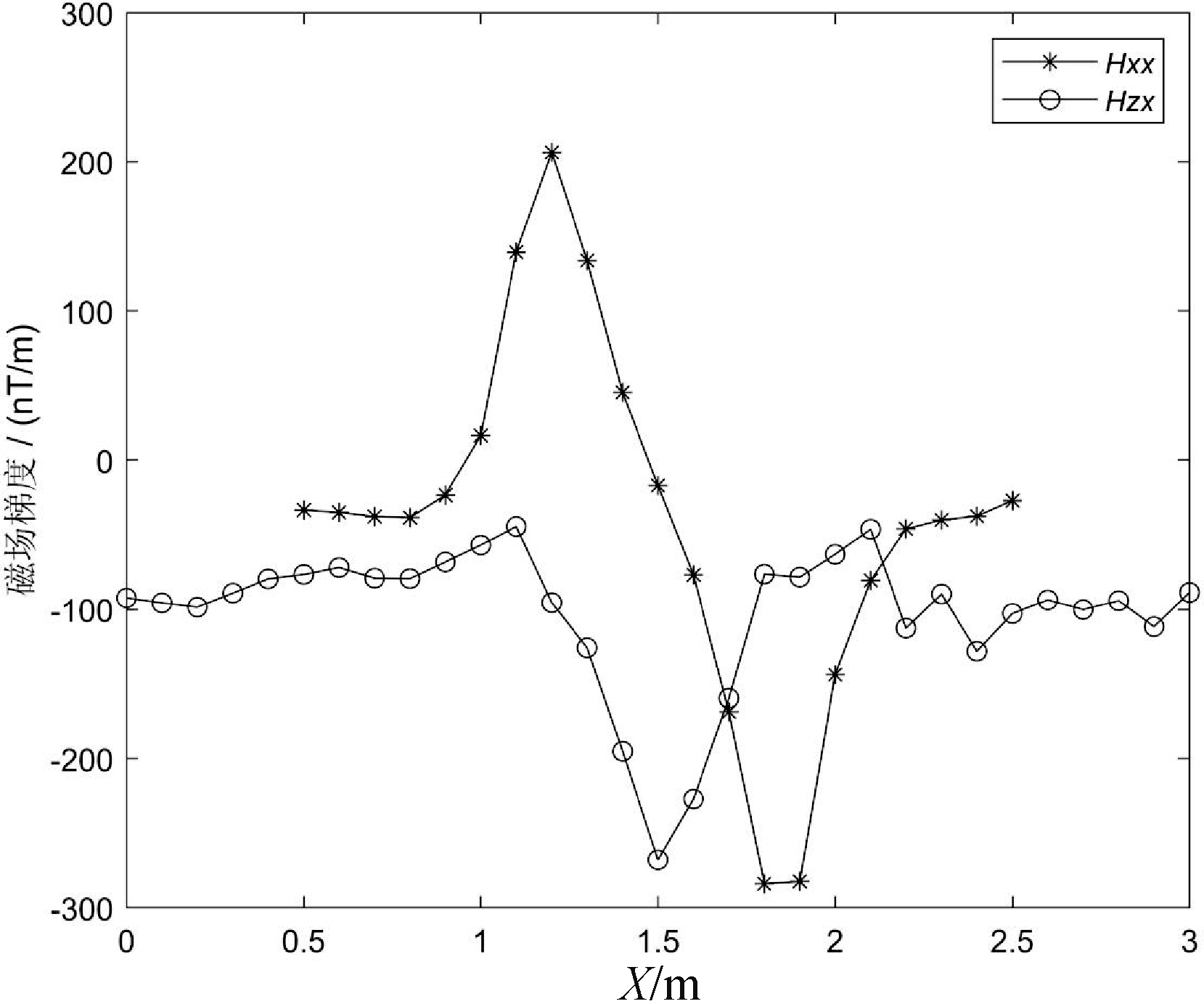
为了消除部分误差,每个测点观测3次,取平均值作为最终值,图14为磁场梯度曲线。水平磁场梯度Hxx有一个极大值和一个极小值,磁探头远离目标体时,Hxx在为-27~-40 nT/m 之间变化,当第一个探头靠近铁块时,磁场梯度增大,最大值为206.37 nT/ m;当铁块位于两个探头的中心时,磁场水平梯度接近于0 nT;当第二个探头经过铁块时,磁场梯度达到最小值-283.97 nT/m。两个极值幅值差别较大的原因可能是两个探头灵敏度不一致,另一个原因可能是测量过程中探头距离铁块的距离误差造成的,毕竟探头距离铁块只有0.3 m。
-
图12 倾斜模型正演结果与偏移成像(模型四)
-
a—异常体x和z方向磁场分量;b—x和z方向磁场分量梯度;c—磁场分量偏移成像;d—磁场分量梯度偏移成像
-
图13 磁场水平梯度和垂直梯度测量示意图
-
在垂直磁场观测中,测线两端磁场梯度Hzx值介于-40~-110 nT/m,当探头经过铁块上方时出现极小值,最小值为-267.97,异常两边基本对称;另外,测线右边的观测数据跳变较大,说明外界干扰较大。噪声与极小值的比值约为27.7%。
-
图14 沿X方向磁场水平梯度HXX曲线
-
根据偏移成像原理,镜像场与其对应原场的特殊性,镜像场的 Hxx与原场的 Hxx相等,但与 Hzx互为相反数,通过镜像场便可以求得伴随算子,进而得到磁化率分布图。通过对实测数据进行偏移成像,结果如图15 所示,目标体成像清楚,磁化率最大值约 0. 05 SI,其中心位置与磁性体横向位置基本一致,为 1.4~1.6 m;偏移成像目标体顶埋深在 0.5 m,而模型的顶埋深为 0.3 m,有一定误差,表明这种方法深度方向分辨率较差。由图14 可知垂直磁场 Hzx 曲线右边受到强噪声干扰,但偏移成像依然能够说明这种算法具有较强的抗噪声能力。
-
3.4 山东齐河—禹城深埋铁矿偏移成像
-
山东省齐河—禹城深埋铁矿位于鲁西黄河沉积平原上,地表平坦,海拔约 20 m,由航磁发现 30 km×20 km巨大的侵入岩体,顶埋深800~1100 m,地面查证时做过 1∶10000 比例尺高精度磁法观测,钻探在 1100~1200 m 深度发现高品位铁矿,图16 为一条北西—南东方向的精测磁异常剖面,长约24 km,对其进行磁偏移成像,当地地磁场为53027 nT,磁偏角约-7°,磁倾角约56°。可以看出,图16a磁异常极大值出现在x=15 km附近,局部地表干扰很大,但相对于主异常来说,干扰数据占比较少,磁偏移成像算法具有很强的抗干扰能力,且速度非常快。图16b 是偏移成像结果,反演的火成岩体磁化率中心位于 x=12 km、深度约-5000 m 处,但浅部磁化率异常位于 x=11 km、深度约-1100 m 处,钻探结果显示该位置有品位为56%的富铁矿,厚度约100 m,这说明磁偏移成像算法具有较好成像效果,值得应用推广。
-
图15 实测磁场梯度数据偏移成像
-
图16 深埋铁矿磁偏移成像
-
a—总磁异常曲线;b—磁偏移成像
-
4 结论
-
(1)针对二维磁场分量或其分量梯度的正交性构建了基于复平面的偏移成像算法,并编写程序,理论模型表明偏移成像算法正确,磁性体的成像位置正确,沿测线分辨率高于沿深度分辨率。
-
(2)对含有较强抗噪声的磁场和磁场梯度理论合成数据进行偏移成像,结果表明,偏移成像算法具有稳健的抗噪声能力。
-
(3)通过物理试验和实测数据的偏移成像结果表明,二维磁场梯度偏移成像效果良好,且不需要进行传统磁场数据的各种校正,简单便捷,成像清晰。
-
参考文献
-
Berkhout A J. 1980. Seismic Migration[M]. Amsterdam: Elsevier.
-
Claerbout J F. 1985. Imaging the Earth’s Interior[M]. Amsterdam: Blackwell Scientific Publications.
-
Kunetz G. 1972. Processing and interpretation of magnetotelluric sounding[J]. Geophysics, 37: 1005-1021.
-
Li Y. 2001. 3D inversion of gravity gradiometer data[C]//71st SEG Meeting, San Antonio, Texas, USA, Expanded Abstracts.
-
Oldenburg D W, Li Y. 1999. Estimating depth of investigation in deresistivity and IP surveys[J]. Geophysics, 64(2): 403-416.
-
Oliveira J V C, Barbosa C F. 2013. 3D radial gravity gradient inversion[J]. Geophysical Journal International, 195(2): 883-902.
-
Schneider W A. 1978. Integral formulation for migration in two and three dimensions[J]. Geophysics, 43: 49-76.
-
Sun J, Li Y. 2015. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering[J]. Geophysics, 80(4): 1-18.
-
Tarantola A, Valette B. 1982. Generalized nonlinear inverse problems solved using the least squares criterion[J]. Reviews of Geophysics, 20(2): 219-232.
-
Zhdanov M S, Booker J R. 1993. Underground imaging by electromagnetic migration[J]. Expanded Abstracts, 77(2): 355-357.
-
Zhdanov M S. 2002. Geophysical Inverse Theory and Regularization Problems[M]. Amsterdam: Elsevier.
-
Zhdanov M S, Ellis R G, Mukherjee S. 2004. Regularized focusing inversion of 3D gravity tensor data[J]. Geophysics, 69: 925-937.
-
Zhdanov M S. 2009a. New advances in 3D regularized inversion of gravity and electromagnetic data[J]. Geophysical Prospecting, 57(3): 463-478.
-
Zhdanov M S. 2009b. Geophysical Electromagnetic Theory and Methods[M]. Amsterdam: Elsevier.
-
Zhdanov M S, Liu X J, Wilson G A, Wan L. 2011. Potential field migration for rapid imaging of gravity gradiometry data[J]. Geophysical Prospecting, 59(6): 1052-1071.
-
Zhdanov M S, Liu X J, Wilson G A. 2012. 3D migration for rapid imaging of total magnetic intensity data[J]. Geophysics 77(2): 1-5.
-
Zhdanov M S, Lin W. 2017. A daptive multinary inversion of gravity and gravity gradiometry data[J]. Geophysics, 82(6): 101-114.
-
高秀鹤, 黄大年. 2017. 基于共轭梯度算法的重力梯度数据三维聚焦反演研究[J]. 地球物理学报, 60(4): 1571-1583.
-
刘天佑, 管志宁. 1986. 对二维磁异常利用广义逆矩阵的选择法[J]. 地球物理学报, 29(4): 390-398.
-
苏士星, 宋双全, 魏明君. 2022. 综合物探方法在河南济源疙瘩深隐伏铁矿床勘查中的应用[J]. 矿产勘查, 13(8): 1191-1197.
-
田明阳, 吴燕冈, 张爽, 颜鸿群, 张瑞森. 2018. 基于重力及重力梯度数据的位场偏移成像[J]. 世界地质, (1): 218- 223.
-
周豪, 李善平, 王亚栋, 逯永卓, 张鑫利, 封建平. 2024. 高精度磁测在柴达木盆地北缘三角顶金矿床找矿中的应用[J]. 矿产勘查, 15(6): 999-1006.
-
摘要
针对目前二维磁场解释中仍然使用人机互动的半定量建模拟合问题,本文基于位场偏移成像理论,通过对镜像磁场源的向上延拓迭代,实现二维磁场及其梯度的正演模拟和偏移成像算法,编写了相关程序。模型计算表明,偏移成像算法得到的磁性体空间位置与模型位置吻合较好,横向分辨率高于纵向分辨率。在抗噪声研究中,给理论磁场数据中增加了多达50%的干扰信号,偏移成像结果依然清楚,表明该算法具有稳健的抗噪声能力。采用物理试验方法获得磁总场梯度实测数据,经偏移成像得到磁性体的位置与试验铁块位置一致,说明该算法能够反演解释野外生产中获得的磁场梯度数据。上述研究表明,二维磁场及其梯度偏移成像算法,性能稳定,抗干扰能力强,自动迭代实现反演成像,简单便捷。
Abstract
Aiming at the semi quantitative modeling and fitting problem of human-computer interaction in the current two-dimensional magnetic field interpretation, based on the potential field migration imaging theory, this paper studies the migration imaging algorithm of two-dimensional magnetic field and its gradient, that is, through the upward continuation iteration of the mirror magnetic field source, the imaging algorithm of magnetic susceptibility is realized, and the forward simulation and migration imaging program are written. The model calculation shows that the spatial position of the magnetic body obtained by the migration imaging algorithm is in good agreement with the model position, and the transverse resolution is higher than the longitudinal resolution. In the anti-noise research, a large interference signal is added to the theoretical magnetic field data. The migration imaging results show that the magnetic body imaging is clear, which shows that the algorithm has robust anti-noise ability. The measured data of magnetic field gradient are obtained by physical experiment method. The position of magnetic body obtained by migration imaging is consistent with the position of experimental iron block, which shows that the algorithm can inverse and interpret the magnetic field gradient data obtained in field production. The above research shows that the two-dimensional magnetic field and its gradient migration imaging algorithm has stable performance, strong anti-noise ability, automatic iterative inversion imaging, simple and convenient, and is worthy of popularization.