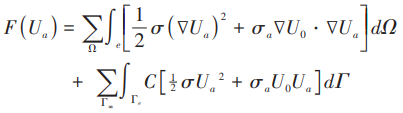-
0 引言
-
直流激电法在探测浅部目标体时具有独特的优势,但随着探测深度的增大,对于常规的几何电测深法,成倍增大供电极距无疑会降低工作效率,增加数据采集成本(Liu et al.,2014a;刘海飞等, 2017)。如果勘探区存在钻井,可以同时借助地表和钻井的观测空间,对常规电测深观测方法加以改进,实现地-井阵列观测,以获取尽可能多的井旁地电信息,对弥补钻孔周围的信息缺失和提高井旁目标体的探测效果大有裨益。
-
井中电法早在 1958 年由前苏联学者提出并成功应用于圈定煤层边界。井-地电法在油气田勘探方面的研究和应用较多,利用生产井套管作为电极,采用井中激发井中测量的观测方式,在美国佐治亚州Roosevelt Hot Springs KGRA圈定了地热层的埋深与分布范围(Sill and Ward,1978①)。在加利福尼亚 Richmond 分校的野外监测站进行了向淡水含水层注入盐水的井-地电阻率监测实验(Bevc and Morrison,1991)。井中垂直双电偶极源建场法被用于预测油气藏的储层边界,振幅及相位异常特征指示明显(何展翔等,2004;Zhan et al.,2004)。井-地直流电法的水槽物理模拟实验结果表明,该方法在油气藏储层预测方面具有可行性,并能够通过校正方法消除多种畸变干扰(张天伦,1990,1993,1994; 张天伦和张伯林,1995;张天伦等,1997),此外,借助低阻或高阻体引起的电位异常能够为水层或油气储层的边界圈定提供参考依据(王志刚等, 2005)。井-地电法在金属矿产勘查方面的研究和应用也较多,井-地直流激电法在加拿大魁北克省西北部Casa Berardi金矿开展了矿产调查工作,确定了含金石英脉型矿体的空间分布范围(Spitzer and Chouteau,2003)。井下径向阵列电探方法被用于调查昆士兰州查特斯塔附近的坎布罗—奥陶纪山温莎火山井旁矿体的分布情况(Stephen,2004)。吕玉增等采用有限单元法,针对井-地激电充电法与地-井五方位测井 2 种方法进行了数值模拟及反演研究,较系统的讨论了相关异常规律,并探讨了实现井中激电三维正反演解释技术(吕玉增,2008;吕玉增等,2012a,2012b)。潘和平(2013)结合野外应用实例,系统阐述了井中激电不同观测方式的基本原理及优势。农观海(2013)提出了一种密集阵列井-地激电观测方法,并开发了相应的三维正演模拟和反演成像解释系统,同时研制了适于该观测方法的分布式观测装置,不仅提高了工作效率,同时具备较高的可靠性和适用性。陈海宏等(2014)设计了地-井激发极化水槽模拟实验,以水体模拟围岩,铜板模拟矿体,研究分析了井中极化场的分布特点。周婷(2015)在总结分析现有的井-地电法技术的基础上,构建井-地三维观测系统,针对 4 种观测系统分别进行了数值模拟和物理模拟实验,结果表明井-地电法能够一定程度上判识水力压裂范围。黄俊革等(2015)采用有限元法实现了径向网格剖分的井-地电阻率三维数值模拟,并设计了相应的井-地观测系统,有效改善了无法确定观测方位的问题。汪洋(2016)利用水槽实验对低阻高极化岩石标本进行了井中激电法物理模拟,并在内蒙古某金属矿区开展了野外试验工作,对比分析了不同装置的勘测结果。综上所述,为获取尽可能多的井旁隐伏矿体的地电信息,进一步研究井中激电地-井三维阵列勘探方法是具有实际意义的。
-
本文在前人研究的基础上,设计了一种井中激电地-井方式三维阵列勘探方法及其观测数据的视记录点,并借助连续电性介质模型异常电位三维有限元数值模拟方法,对不同地电模型模拟的视电阻率和视极化率响应进行了模拟分析,从模拟结果来看,该阵列观测方法可以获得更加丰富的井旁信息,可为划分井旁矿体的空间分布提供参考依据。
-
1 井中激电地-井方式三维阵列观测方法
-
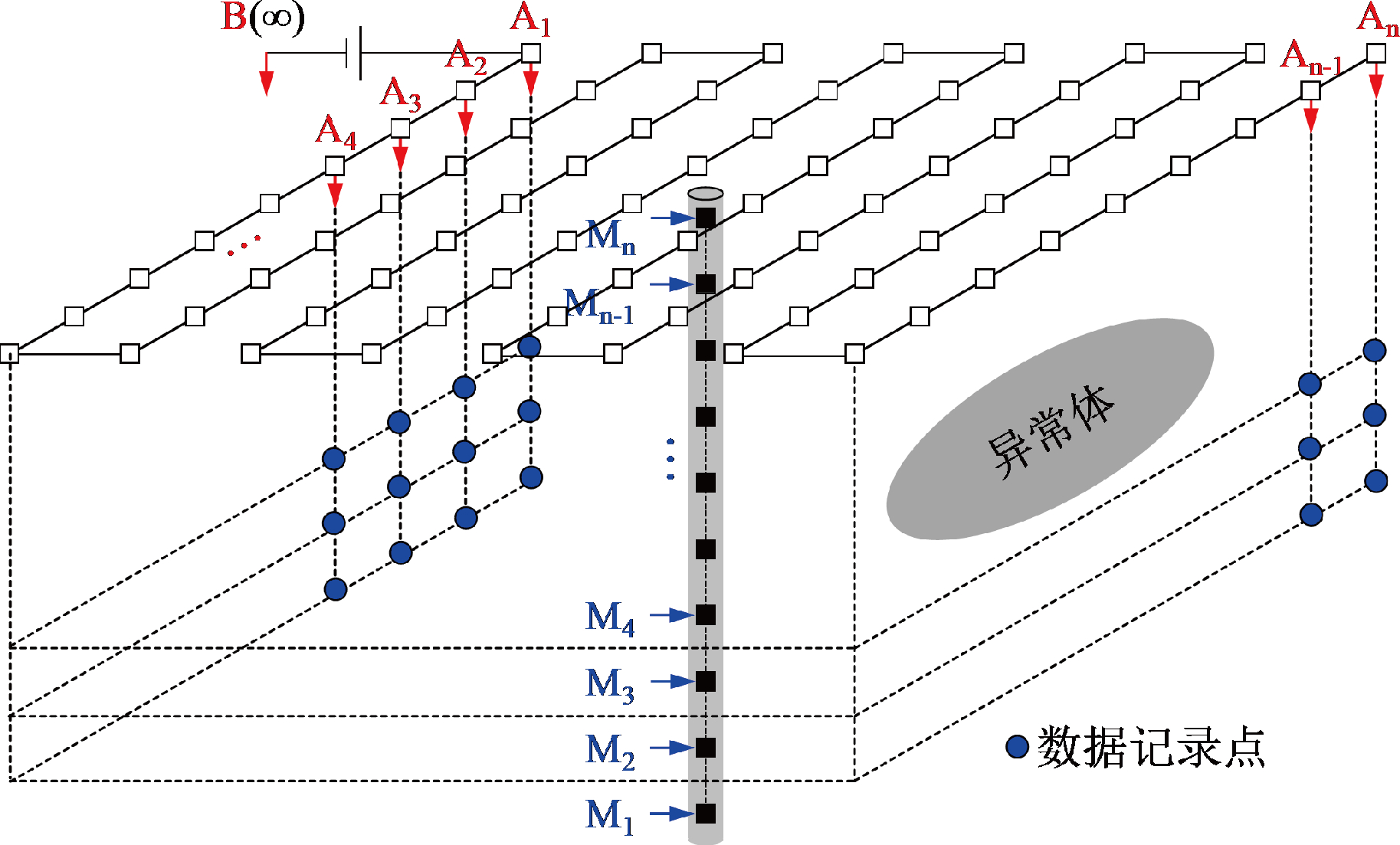
井中激电地-井方式勘探方法是在地表向地下供入电流,在井中采集电位差信号的数据采集方式,地-井观测方式能有效提高横向分辨率。目前地-井观测方式主要采用地-井五方位,即在地表合理位置布置5个供电点。本文设计了一种井中激电地-井方式三维阵列观测方法(图1)。该方法的数据采集过程:首先将供电负极 B 布置在较远处作为无穷远极,然后发射系统通过供电正极 Ai(i=1,2, ···,n)向地下供电并实时记录发射电流,接收系统依次采集井中测量电极对 MiMi+1(i=1,2,···,n-1)采集一次场和二次场电位差信号;供电电极 A2供电,测量电极 MiMi+1(i=1,2,···,n-1)采集一次场和二次场电位差信号;直到供电电极 An供电,测量电极 MiMi+1(i=1,2,···,n-1)采集一次场和二次场电位差信号,数据采集完毕。为便于数据分析,可将供电电极的平面坐标(x,y)和测量电极 MiMi+1(i=1,2, ···,n-1)的中点 z作为数据的视记录点(x,y,z)。该方法可根据场地观测条件和目标体的分布情况合理设计供电点位置。
-
图1 地-井方式三维阵列观测方法示意图
-
2 井中激电三维有限元数值模拟
-
2.1 异常电位的边值问题与变分问题
-
为提高电位场的数值模拟精度,通常将总电位的边值问题转化为异常电位的边值问题进行求解。地下介质的电导率 σ 可以分解为场源处的电导率σ0 与异常电导率 σa 之和,即 σ = σ0 + σa,总电位 U 为正常电位 U0与异常电位 Ua之和,即 U = U0 + Ua。结合地表和地下研究区域的边界条件,三维异常电位的边值问题(徐世浙,1994):
-
对于正常电位 U0,当点源 A 位于地表时,U0 = I/2πσ0 rAP;当点源 A 位于地下时,U0 = I/4πσ0 rAP + I/4πσ0 rA'P,上式中 rAP 和 rA'P 分别为点源 A 及其相对地表的镜像源A'到地下空间任一点P的距离。与边值问题对应的变分问题为:
-
2.2 连续介质模型异常电位三维有限元数值模拟
-
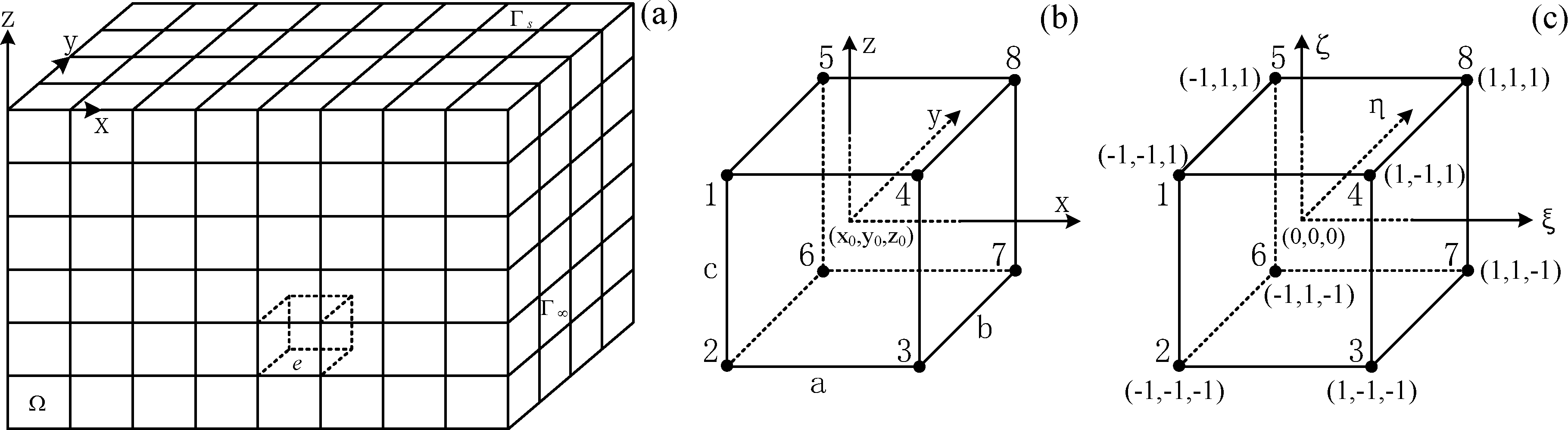
对研究区域 Ω进行六面体单元剖分(图2a),式 (2)中对 Ω 的积分可拆分为对单元 e 和边界 Γe 的积分之和:
-
考虑到地下介质的物性随温度、湿度和压力的变化而变化,因此在单元内电位场及电导率均采用三线性插值(阮百尧和熊彬,2002):
-
式(4)中 U0i 、Uai、σi 、σai 分别表示节点 i = 1,2,···,8的正常电位(V)、异常电位(V)、正常电导率(S/m)、异常电导率(S/m);形函数Ni为:
-
式(5)中ξi,ηi,ζi为点i的坐标,如图2c所示。
-
根据式(3)对研究区域的各单元积分,并按节点编号位置累加,可得:
-
图2 研究区域剖分示意图
-
a—研究区域Ω剖分示意图;b—子单元示意图;c—母单元示意图
-
式(6)中 K 和 Ka 为刚度矩阵。再令式(6)的变分等于零,得:
-
通过求解式(7)可得异常电位 Ua,与正常电位 U0相加可得全部节点的总电位U。
-
2.3 超松弛预条件共轭梯度法
-
线性方程组(7)的系数矩阵往往是大型、对称、稀疏的,并且是非正定的,具有一定的病态特征。采用预条件共轭梯度法(Preconditioned Conjugate Gradient method, PCG)求解此类方程组在计算效率和占用内存方面是非常有优势的(胡家赣,1999; Liu et al.,2014a)。
-
对于线性方程组:
-
如果系数矩阵 K 的条件数越小,右端项 b 的细微变化引起的解 x 的变化越小,因此收敛性越好。故引入预条件矩阵 M来降低系数矩阵 K的条件数,考虑到K为对称矩阵,设M为K的一个近似分解:
-
则可将方程(8)变换为:
-
设F = L-1KL-T,y = LTx,d = L-1b,有:
-
通过求解方程组(11),可以代替求解方程组 (8)。实际上近似估计可知:
-
(单位阵),因此,若 LLT越近似于系数矩阵 K 的完全分解,F 则越接近 I。那么 F的条件数也就越接近于 1,从而达到改善条件数的目的。
-
为了不破坏原始矩阵,首先将系数矩阵 K 分解为:
-
其对应的超松弛预条件矩阵定义为(Liu et al.,2014a):
-
其中 L 表示下三角阵,D 表示对角阵,ω 表示超松弛因子(1 ≤ ω <2)。超松弛预条件共轭梯度法的迭代过程如下(William et al.,1992):
-
(1)设置初始x0,g0 = b-Kx0,p0 = h0 = M-1g0。
-
(2)开始迭代:
-
(3) 判断是否小于设定的界限( gi + 1,hi + 1)/( g0,h0)<ε = 10-10。若不小于重复步骤(2),直至小于设定的ε,迭代过程结束。
-
在迭代过程中,形如(a,b)表示向量 a和 b的内积;i为迭代序号;g 表示梯度,p 为共轭方向向量;h 表示中间临时向量;αi 为 x 的修正因子,βi + 1 为 p 的修正因子。在上述迭代过程中,不必存储预条件矩阵 M。对于 hi + 1 = M-1gi + 1,无需对其进行求解,通过移项转化为方程组的形式Mhi + 1 = gi + 1,然后采用高斯消去法通过顺代和回代得到 hi + 1,该过程仅涉及少数非零元素间的相加和相乘,减少了计算量。
-
2.4 计算视电阻率/视极化率
-
根据电位的模拟结果换算出视电阻率,即
-
式(14)中ΔU表示电位差,I表示电流强度,K表示装置系数。在野外工作中,不论在地表还是地下观测,采集一个视电阻率数据通常需要两个供电电极和两个测量电极,即供电电极 A和 B、测量电极 M 和N。这样装置系数K可写为:
-
式(15)中 rAM、rBM、rAN和 rBN分别为供电电极 A、B 到测量电极 M、N 的距离,rA'M、rB'M、rA'N 和 rB'N 分别为供电电极 A、B 关于地表的镜像电极 A'、B'到测量电极M、N的距离;任意四极观测装置的装置系数均可由式(14)进行计算。
-
极化率的正演模拟是根据Seigel的体激发极化理论,即如果地下介质具有体极化特性,等效电阻率可表示为:
-
式(16)中 ρ 为介质的电阻率,η 为介质的极化率。基于等效电阻率模型式(10),等效视电阻率 可以写为:
-
式(17)中 ηs 表示视极化率。利用电阻率的数值模拟方法,可以得到视电阻率 ρs和等效视电阻率 ,进而可换算出视极化率:
-
3 模拟分析
-
根据上述算法,基于 VC++开发平台编制了直流激电人机交互三维数值模拟软件 DCIP3DMod。利用该软件对井中激电三维阵列观测的电阻率和极化率异常响应进行了模拟分析。
-
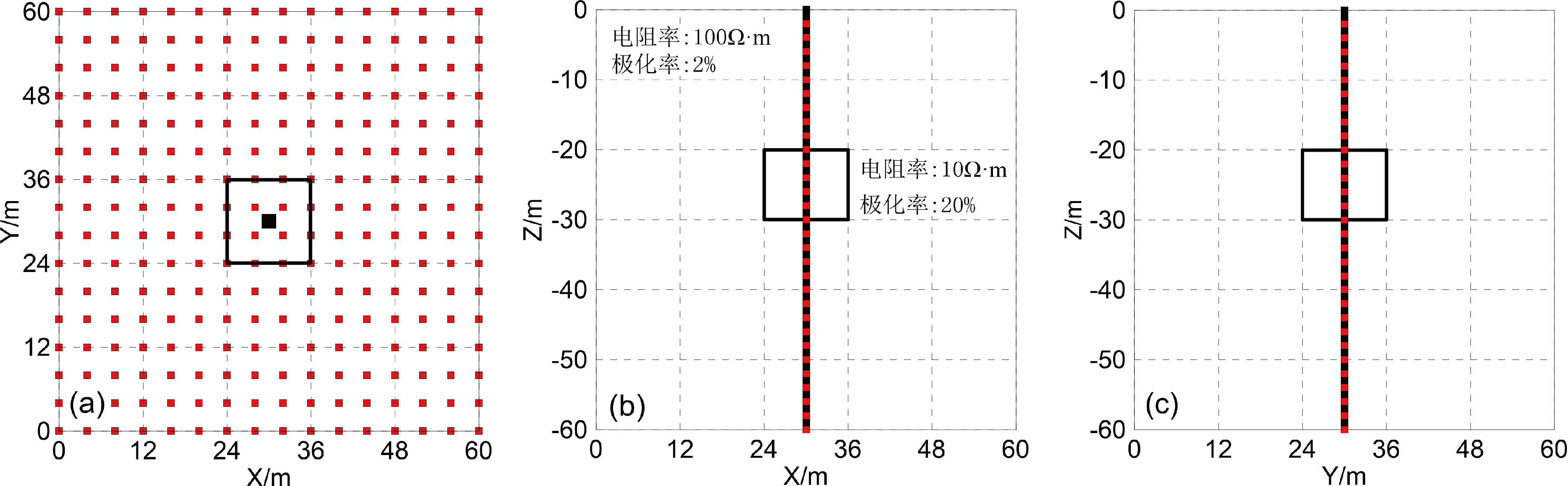
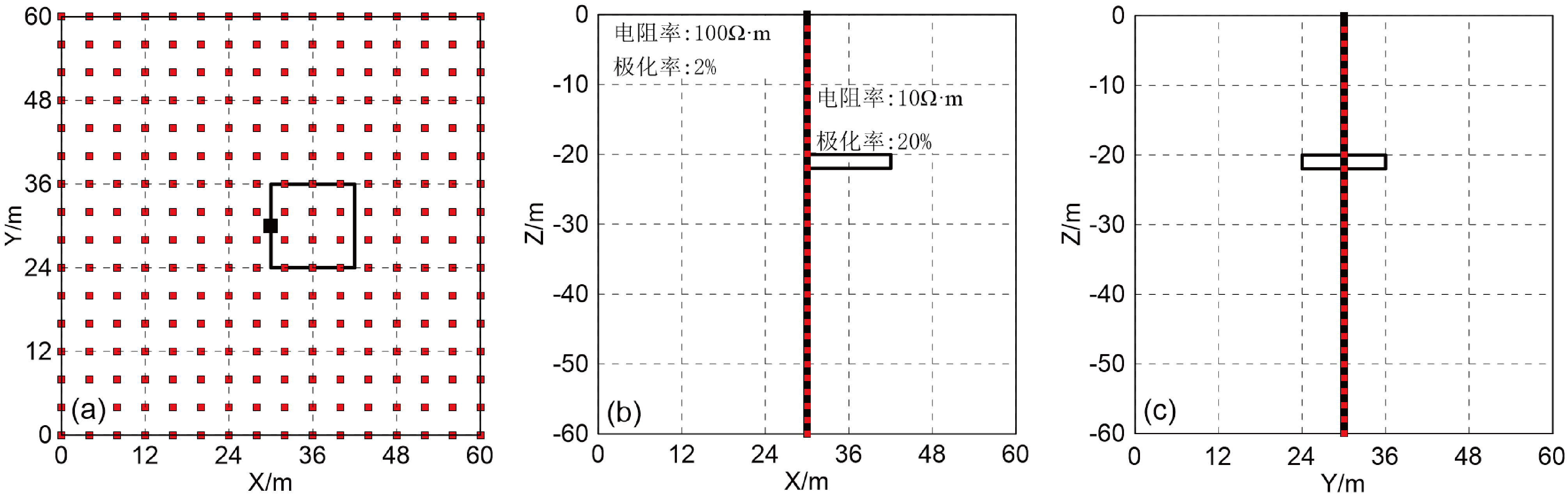
(1)模型一:地下均匀半空间的电阻率和极化率分别为 100 Ω·m 和 2%,异常体的电阻率和极化率分别为 10 Ω·m 和 20%。异常体的顶板距离地面 20 m,异常体的长、宽、高分别为 12 m、12 m、10 m。钻孔井口坐标为(30,30,0)(图3a 中黑色方形点),钻孔垂直穿过异常体,异常体相对钻孔对称。地表供电电极按 4 m间距布设,供电电极点位 256个(图3a 中红色方形点),井中测量电极按 2 m 间距布设,测量电极点位 30 个。地电模型具体如图3 所示。对模型一采用 2 m 单元剖分整个区域,剖分节点总数106641(51×51×41)个,模拟地表所有供电点(256 个)的激电测井曲线。
-
图3 模型一
-
a—Z=0 m的XOY平面切片;b—Y=30 m的XOZ平面切片;c—X=30 m的YOZ平面切片
-
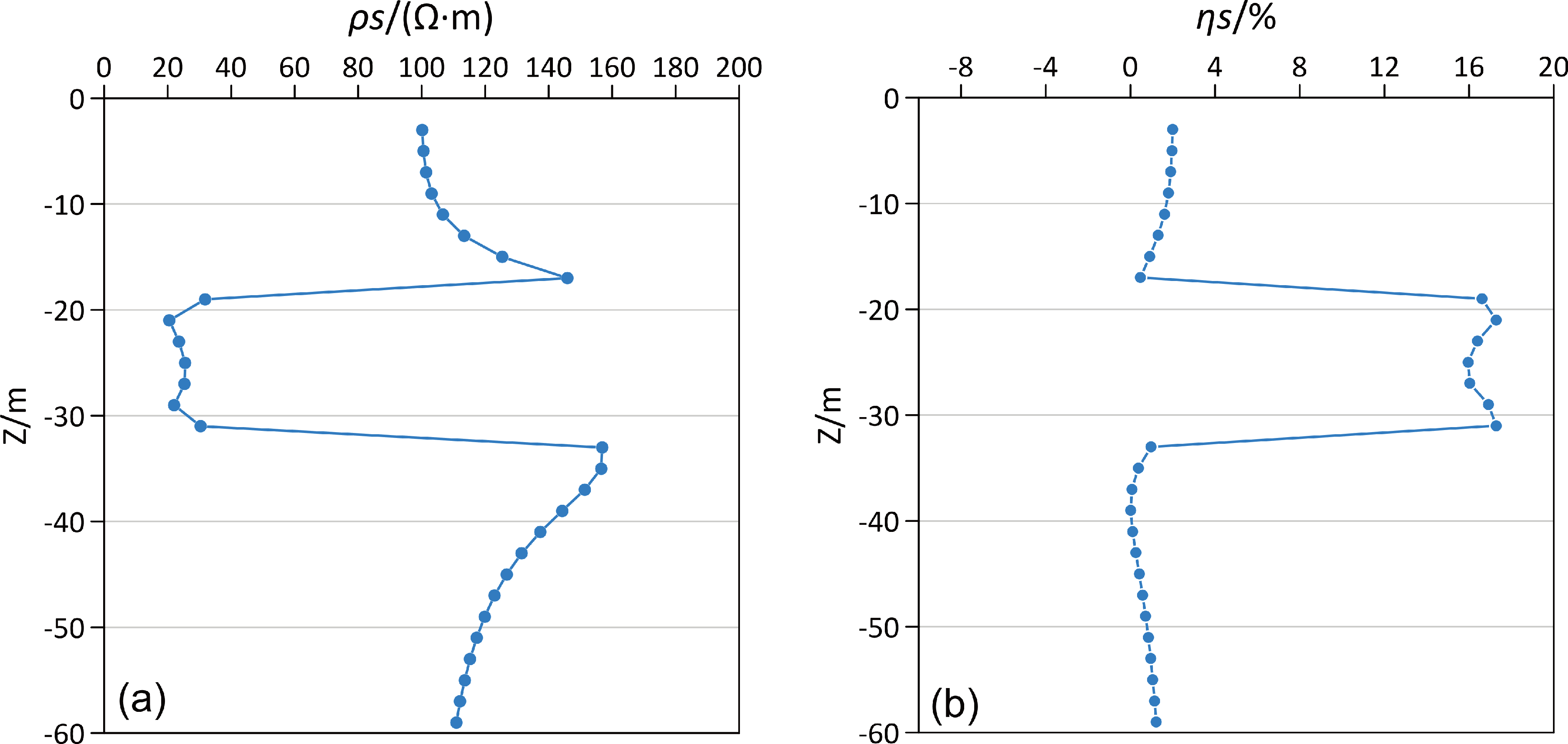
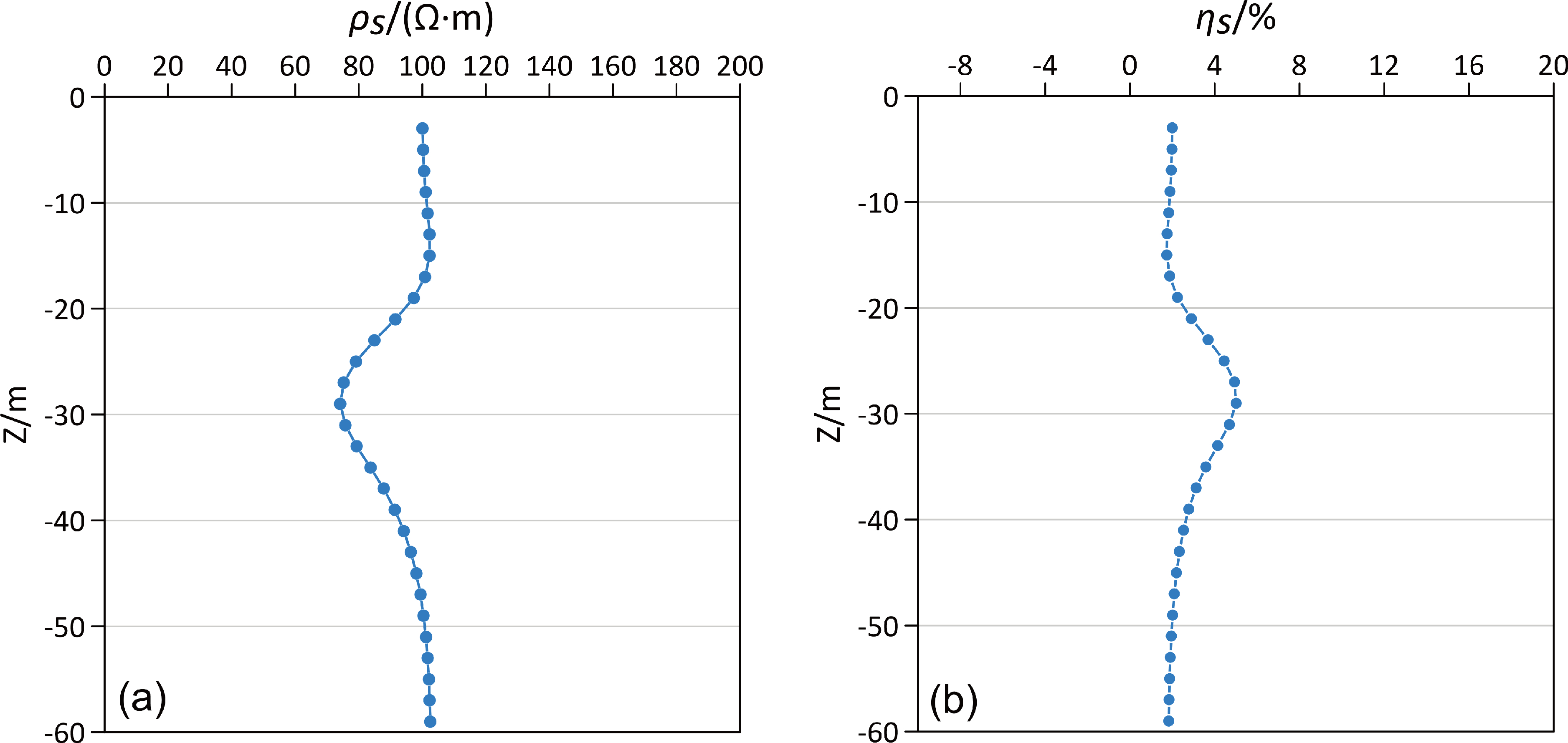
图4 为模型一供电点在(28,28,0)处的视电阻率和视极化率模拟曲线,可以看出在-20~-30 m 深度段,曲线总体呈低阻高极化特征,而在异常体上下方与围岩的接触带附近曲线呈明显的高阻低极化特征,并且视电阻率高于背景电阻率,视极化率低于背景极化率,这种特征可以作为推断异常体顶底板埋深的有效标志。
-
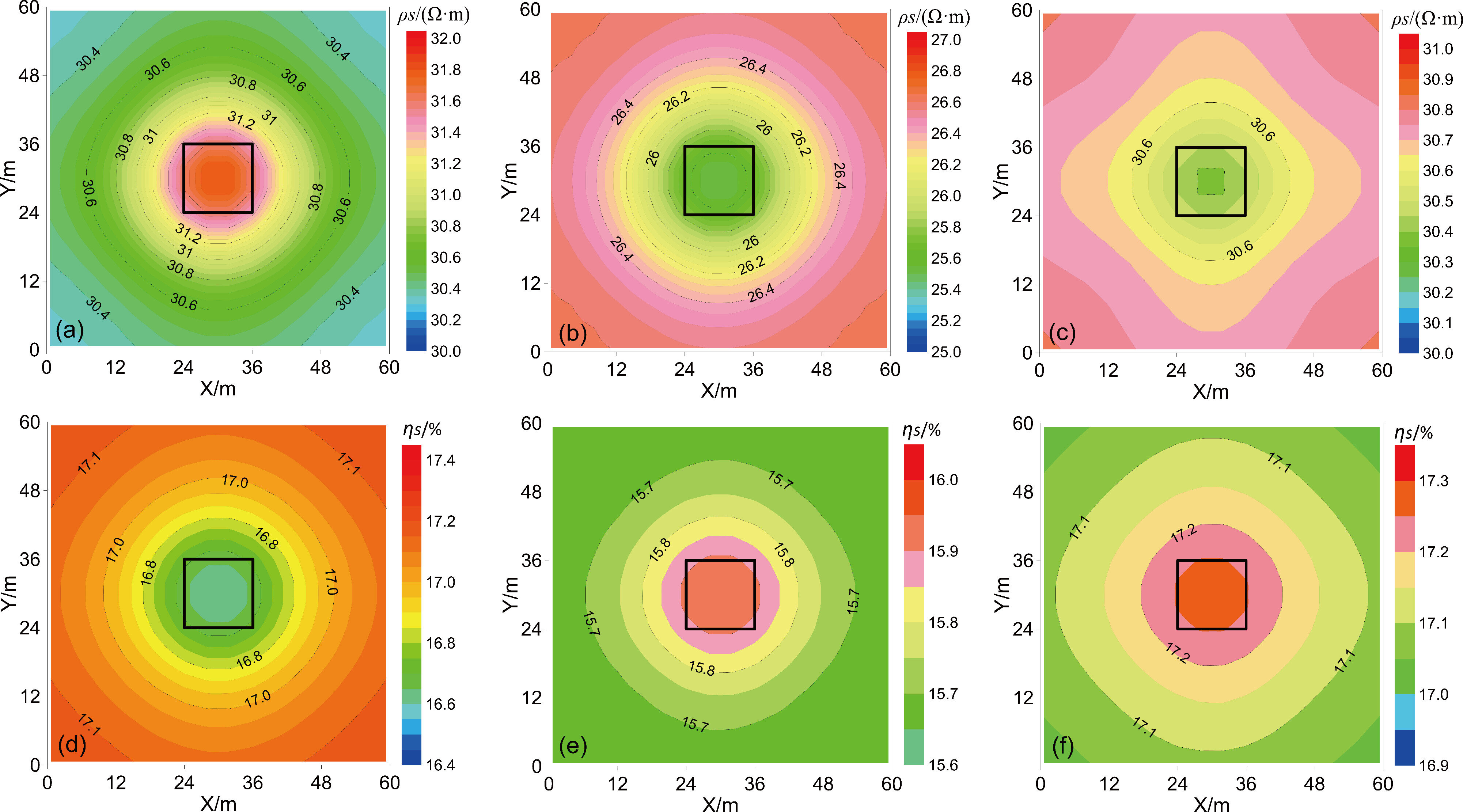
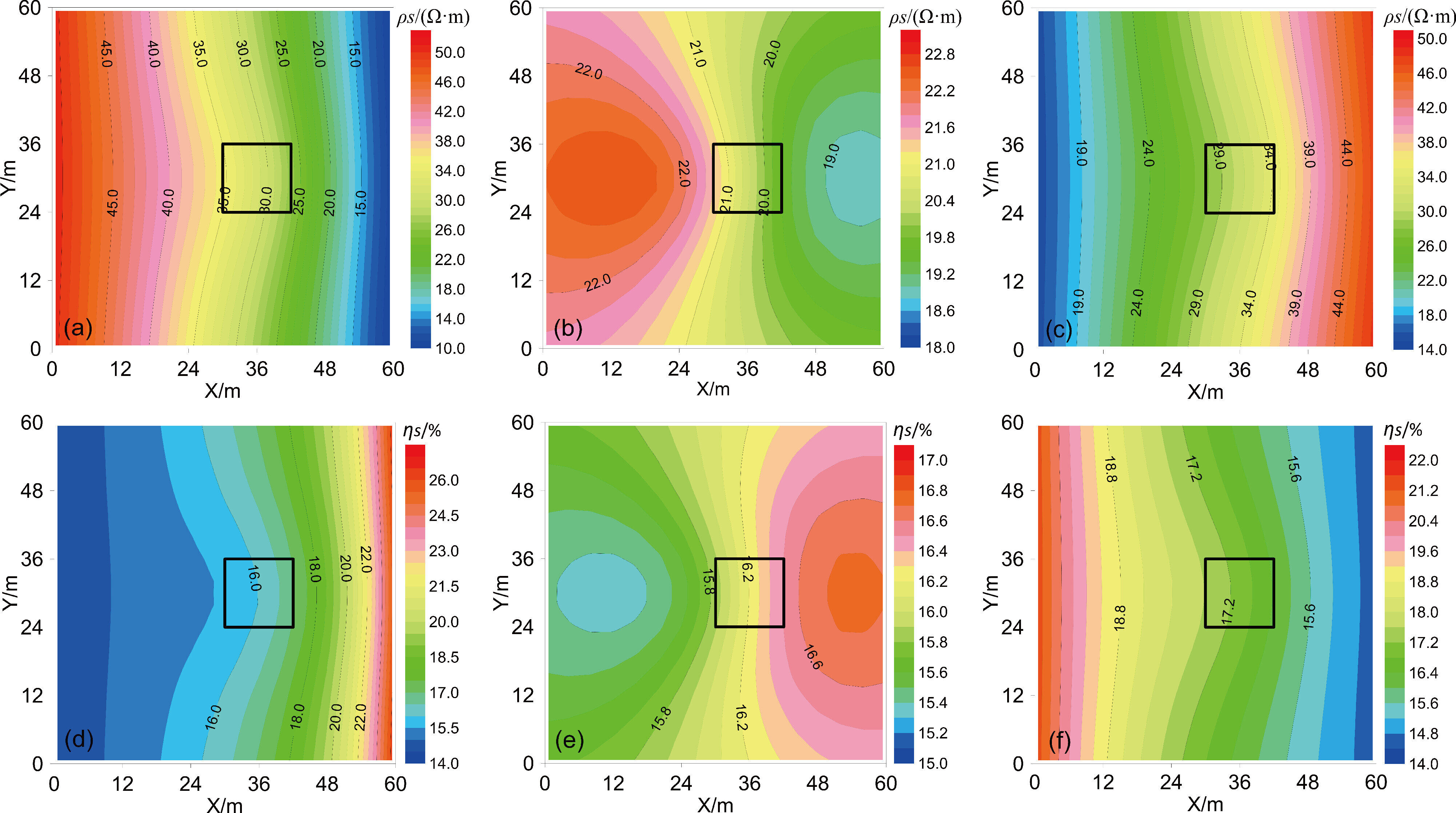
抽取所有激电测井曲线在-19 m、-25 m和-31 m 深度的视电阻率和视极化率数据,绘制平面等值线图(图5),其中图5a~c 和图5d~f 分别为-19 m、-25 m、-31 m 深度的视电阻率和视极化率等值线图。由图5a和图5d可知,在异常体顶板中心位置呈高阻低极化特征,视电阻率向四周逐渐减小,视极化率向四周逐渐增大。而在异常体中间和底板的中心位置呈低阻高极化特征,并且视电阻率向四周逐渐增大,视极化率向四周逐渐减小(图5b~c;图5e~f)。总体来看,异常体中间切片(-25 m)的视电阻率和视极化率均小于顶板切片(-19 m)和底板切片(-31 m)的视电阻率和视极化率。对于相对钻孔较为对称的目标体,这些特征有助于推断异常体的平面分布范围和中心埋藏深度。
-
图4 模型一供电点在(28 m,28 m,0 m)的视电阻率(a)和视极化率(b)模拟曲线
-
图5 模型一不同深度的视电阻率和视极化率平面等值线图
-
a~c—-19 m、-25 m和-31 m深度的视电阻率等值线图;d~f—-19 m、-25 m和-31 m深度的视极化率等值线图
-
(2)模型二:模型电性参数、电极布设、井位和网格剖分等均与模型一相同,仅将低阻高极化异常体移至钻孔右侧,异常体的厚度调整为2 m,具体如图6所示。
-
图6 模型二
-
a—Z=0 m的XOY平面切片;b—Y=30 m的XOZ平面切片;c—X=30 m的YOZ平面切片
-
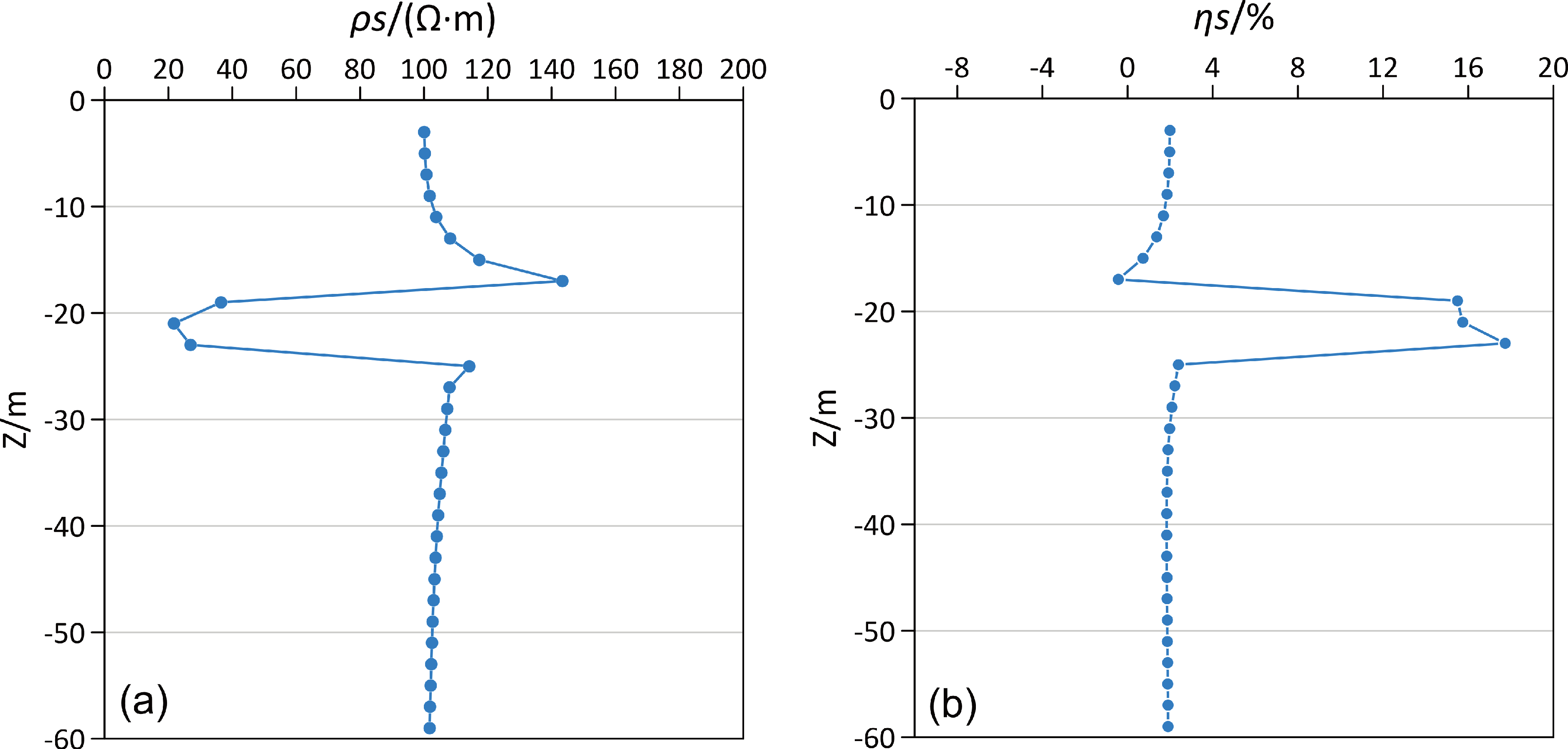
图7 为模型二供电点在(28,28,0)处的视电阻率和视极化率模拟曲线,在-20~-22 m 深度段曲线总体呈低阻高极化特征,而在异常体上方与围岩的接触带附近曲线呈明显的高阻低极化特征,并且视电阻率高于背景电阻率,视极化率低于背景极化率,而在异常体下方与围岩的接触带附近曲线呈高阻高极化特征,视电阻率和视极化率均高于背景,这种特征亦可作为推断异常体顶底板埋深的有效标志。
-
图7 模型二供电点在(28 m,28 m,0 m)的视电阻率(a)和视极化率(b)模拟曲线
-
抽取所有激电测井曲线在-19 m、-21 m 和-23 m 深度的视电阻率和视极化率数据,绘制平面等值线图(图8),其中图8a~c 和图8d~f 分别为-19 m、-21 m、-23 m深度的视电阻率和视极化率等值线图。由图8a~b 和图8d~e 可知,在钻孔左侧异常呈高阻低极化特征,而在钻孔右侧异常呈低阻高极化特征,异常体位置的等值线梯度变化较大,而底板异常特征却表现为钻孔左侧呈低阻高极化、钻孔右侧呈高阻低极化,与上部切片的异常特征恰恰相反 (图8c,图8f)。与模型一的异常对比,异常体中间切片(-21 m)的视电阻率和视极化率均小于顶板切片(-19 m)和底板切片(-23 m)的视电阻率和视极化率。对于在钻孔一侧的目标体,这些特征可以作为推断异常体的平面分布和中心埋藏深度的参考依据。
-
图8 地电模型二不同深度的视电阻率和视极化率平面等值线图
-
a~c—分别为-19 m、-21 m和-23 m的视电阻率等值线图;d~f—分别为-19 m、-21 m和-23 m的视极化率等值线图
-
(3)模型三:在井旁埋设 2 个低阻高极化异常体,而模型电性参数、电极布设、井位和网格剖分等均与模型一相同,具体如图9所示。
-
图9 模型三
-
a—Z=0 m的XOY平面切片;b—Y=30 m的XOZ平面切片;c—X=30 m的YOZ平面切片
-
图10为模型三供电点在(28,28,0)处的视电阻率和视极化率模拟曲线,在-20~-40 m 深度段曲线总体呈低阻高极化特征,曲线比较平滑,异常幅度变小,上下异常界面不明显,曲线峰值位置在-29 m 处,相对异常体中心深度(-25 m)下移4 m。当异常体与钻孔存在一定距离时,异常幅度将减弱,异常峰值深度大于目标体实际埋深,这种现象是异常推断解释时应该引起注意的。
-
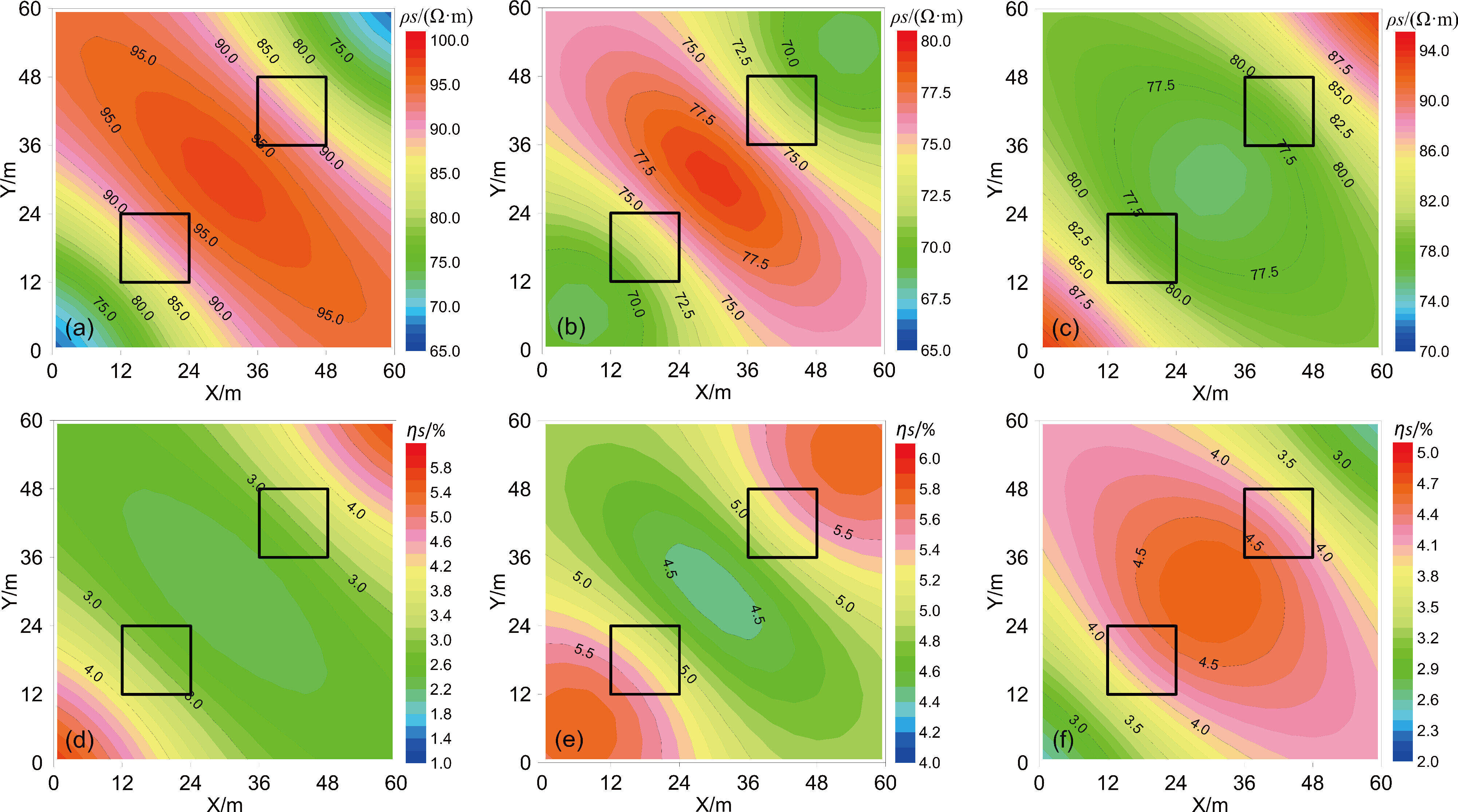
抽取所有激电测井曲线在-19 m、-25 m和-31 m 深度的视电阻率和视极化率数据,绘制平面等值线图(图11),其中图11a~c 和图11d~f 分别为-19 m、-25 m、-31 m 深度的视电阻率和视极化率等值线图。由图11a~b 和图11d~e 可知,异常体顶板和中间切片在井口附近呈现北西走向的高阻低极化异常,其走向基本垂直于两异常体的连线方向,两异常体处等值线的梯度变化较大,而异常体底板切片的异常特征恰恰相反,呈现出低阻高极化特征。总体来看,在异常的梯度带处中间切片仍然表现出相对的低阻高极化特征。对于钻孔附近不连续的目标体,异常带走向并非目标体的实际延伸方向,而是在其垂直方向的梯度带上,这种特征可以作为异常推断解释的参考依据。
-
图10 模型三供电点在(28 m,28 m,0 m)的视电阻率(a)和视极化率(b)模拟曲线
-
图11 模型三不同深度的视电阻率和视极化率平面等值线图
-
a~c—分别为-19 m、-25 m和-31 m深度的视电阻率等值线图;d~f—分别为-19 m、-25 m和-31 m深度的视极化率等值线图
-
4 结论
-
本文对井中激电地-井方式三维阵列观测方法进行了研究,得到以下结论:
-
(1)设计了一种井中激电地-井方式三维阵列观测方法,相对传统地-井五方位观测方法,该方法获取的数据信息量得到极大增加。
-
(2)给出了连续电性介质模型井中激电三维有限元数值模拟方法,并采用超松弛预条件共轭梯度法求解大型、稀疏、对称线性方程组。开发了井中激电三维有限元模拟软件DCIP3DMod,可用于井中激电三维阵列观测模型的数值模拟分析。
-
(3)对井中激电地-井方式的三维阵列观测模型进行了数值模拟分析,总体来看,该方法获取的信息量较大,在目标体的空间分布不是非常复杂的情况下,相关图件在纵向上对目标体的顶底板界面指示较明显,而在横向上对目标体的位置和形态的指示不够清晰。实际勘探中需要结合地质情况构建地电模型,并开展模拟实验分析,才能对异常体的空间分布给出合理的地质解释,必要时需要借助井中激电三维反演处理手段,提高解释精度。
-
注释
-
① Sill W R, Ward S H.1978. Electrical Energizing of Well Casings [R]. Utah: Department of Geology and Geophysics,University of Utah.
-
参考文献
-
Bevc D, Morrison H F. 1991. Borehole-to-surface electrical resistivity monitoring of a salt water injection experiment[J]. Geophysics, 56(6): 769‒777.
-
Liu H F, Guo Z W, Liu J X, Guo R W, Ma C Y. 2014a. 3D DCIP inversion using the finite-element approach with variable elements[C]//Near-surface Geophysics and Environment Protection, 697‒706.
-
Liu H F, Liu J X, Guo R W, Tong X Z, Gong L, Peng Y H. 2014b. Research on multi-channel observation and inversion for IP electrical sounding method[J]. Transactions of Nonferrous Metals Society of China, 24(3): 816‒823.
-
Spitzer K, Chouteau M. 2003. A dc resistivity and IP borehole survey at the Casa Berardi gold mine in northwestern Quebec[J]. Geophysics, 68(2): 453‒463.
-
Stephen T M. 2004. Radial Resistivity/IP surveys using a downhole current electrode[J]. Exploration Geophysics, 35(3): 188‒193.
-
William H P, Saul A T, William T V. 1992. Numerical Recipes in C: The Art of Scientific Computing[M]. Cambridge: Cambridge University Press.
-
Zhan X, He X J, Qiu W T, Zhou H. 2004. Mapping reservoir boundary by using borehole-surface TFEM technique: Two case studies[J]. Seg Technical Program Expanded Abstracts, 23(1): 2586.
-
陈海宏, 马火林, 杨志成. 2014. 地-井方式井中激电模型实验[J]. 工程地球物理学报, 11(5): 635‒638.
-
何展翔, 刘雪军, 裘尉庭, 黄州. 2004. 大功率井-地电法油藏边界预测技术及效果[J]. 石油勘探与开发, 31(5): 74‒76.
-
胡家赣. 1999. 线性代数方程组的迭代解法[M]. 北京: 科学出版社.
-
黄俊革, 李林杰, 农观海, 闫怀超, 高文利, 林振洲. 2015. 基于径向剖分的井-地三维有限元电阻率与极化率模拟[J]. 成都理工大学学报(自然科学版), 42(6): 753‒761.
-
刘海飞, 柳建新, 麻昌英. 2017. 直流激电反演成像理论与方法应用[M]. 长沙: 中南大学出版社.
-
吕玉增. 2008. 地-井、井-地IP三维快速正反演研究[D]. 长沙: 中南大学.
-
吕玉增, 阮百尧, 彭苏萍. 2012a. 井-地三维激发极化数据快速反演[J]. 物探与化探, 36(3): 155‒160.
-
吕玉增, 陈百尧, 彭苏萍. 2012b. 地-井方位激电人机交互解释软件开发及应用[J]. 物探化探计算技术, 34(3): 358‒364.
-
农观海. 2013. 井-地密集阵列激发极化法观测系统的研究[D]. 桂林: 桂林理工大学.
-
潘和平. 2013. 井中激发极化法在矿产资源勘探中的作用[J]. 物探与化探, 37(4): 620‒626.
-
阮百尧, 熊彬. 2002. 电导率连续变化的三维电阻率测深有限元模拟[J]. 地球物理学报, 45(1): 131‒138.
-
汪洋. 2016. 井中激电法探测金属矿应用研究[D]. 北京: 中国地质大学(北京).
-
王志刚, 何展翔, 魏文博, 邓明. 2005. 井-地电法三维物理模型试验[J]. 石油地球物理勘探, 40(5): 122‒125.
-
徐世浙. 1994. 地球物理中的有限单元法[M]. 北京: 科学出版社.
-
张天伦. 1990. 用直流电阻率法确定油气藏边界的初步实验[J]. 石油地球物理勘探, 25(5): 584‒593.
-
张天伦. 1993. 井中有套管情况下用直流电阻率法确定油气藏边界的实验与研究[J]. 石油地球物理勘探, 28(3): 314‒324.
-
张天伦. 1994. 使用线电极供电的直流电阻率法预测砂岩构造型油气藏的实验与研究[J]. 石油地球物理勘探, 29(3): 337‒347.
-
张天伦, 张伯林. 1995. 消除直流电阻率三极梯度法中各种干扰的实验与研究[J]. 石油地球物理勘探, 30(1): 100‒110.
-
张天伦, 张伯林, 聂荔. 1997. 用地-井工作方式的三极梯度法寻找小块油气藏[J]. 石油地球物理勘探, 32(4): 520‒531.
-
周婷. 2015. 井-地电法测试模拟实验研究[D]. 淮南: 安徽理工大学.
-
摘要
中国浅表矿、易采矿资源日趋枯竭,迫切需要在现有矿山开展深部找矿,研究适用于深部找矿的地球物理勘探新方法具有重要意义。本文探讨研究了井中激电地-井方式三维阵列观测方法,借助连续电性介质模型异常电位三维有限元数值模拟方法,对不同地电模型模拟的视电阻率和视极化率响应进行了模拟分析。研究结果表明:该方法有效拓展了观测空间,携带目标体信息丰富,可以有效从不同点位和层位提取曲线数据和切片数据,通过绘制相应图件从而分析目标异常的空间分布特征。本文模型分析结果可以作为异常推断解释的参考依据。
Abstract
Easy shallow mining of mineral resources in our country are depleting, urgently need to carry out deep mineral exploration in existing mines. It is of great significance to study new geophysical exploration methods suitable for deep exploration. This article studies the ground-to-well three-dimensional array exploration method of induced polarization in the well, and uses the three-dimensional finite element numerical simulation method for abnormal potential in a continuous electrical medium model to simulate and analyze the apparent resistivity and apparent polarization response of different geoelectric models. The research results indicate that this method effectively expands the observation space, obtains rich target body information, and can conveniently extract curve data and slice data from different points and layers. By drawing corresponding graphs, the spatial distribution characteristics of target anomalies can be analyzed. The model analysis results in this article can provide reference basis for anomaly inference and interpretation.