0 引言

电磁法是矿产勘查的重要手段之一。可控源电磁法具有抗干扰能力强、工作效率高等优点，自提出以来已获得了广泛的应用和发展（Goldstein and Strangway，1975；汤井田和何继善，2005）。由于场源效应的影响，可控源电磁法的阻抗响应在近区和过渡区内往往会产生畸变，难以提取测深信息，因此实际中数据观测通常要求在远区进行（何继善，1991）。如何利用近区和过渡区信息，成为长期受关注的话题。突破非远区频率测深理论，将有力推动电磁法的进步。广域电磁法是何继善院士提出的一种具有完全自主知识产权的人工源频率域电磁测深法（何继善，2010）。该方法从场的统一性出发，将“近区”、“过渡区”和“远区”有机地统一起来，定义广域视电阻率，改善了非远区的畸变效应，使得测深能在广大的、不局限远区的区域进行，且在同等收发距上勘探深度增大。目前，广域电磁法已经在金属矿产、石油及页岩气、煤矿及地热等多种资源探测领域中取得了成功应用（He，2018；刘磊等，2022；李星等，2024）。广域视电阻率的计算从总场出发，能够较好的保障观测精度。然而，由于总场中具备频率测深能力的二次场在近区条件下远小于一次场，因此基于总场计算的广域视电阻率方案在近区的测深能力极为有限。以当前最为常用的广域电磁法 E-Ex 观测模式为例，基于总场计算的 E-Ex 广域视电阻率在近区常呈渐近线形式，不随频率变化，也不具备频率测深意义。

关于近区频率测深学界多有争论（McNeill and Bosnar，1999^①；Huang，2005；Guillemoteau et al.， 2015；罗志亮等，2024），一直在反复进行探索和论证。频率测深理论的关键在于视电阻率的定义方案，国内外已涌现了多种频率域全区视电阻率计算方案（汤井田和何继善，1994；汤井田等，2011）。 Kaufman and Keller（1983）推导了层状介质表面垂直磁偶极子源形成的电磁场分量，并根据双层介质表面电磁场分量的渐进表达式，指出在近区，表达式中感应数的低阶项主要受上层电阻率和厚度控制，而感应数的高阶项仅由基底电阻率控制。据此提出了双频测深的设想，即通过双频测量和计算，设法消去与频率成正比的感应数低阶项、突出感应数高阶项，从而达到小感应数条件下近区测深的目的。基于这一思路，苏发和何继善（1996a，1996b）、苏发等（1996）利用磁场垂直分量，设计了以双频组合波进行频率测深的理论方案，并指出该方案具备近区测深的能力。随着 E-Ex广域电磁法的成功应用，利用电场进行近区双频测深的探索受到了关注 （王庆乙，2021）。王庆乙（2022）提出了水平电偶极子源条件下的广域电磁法近区视电阻率计算方案，通过观测随频率变化的电场 Ex 的虚分量并做双频运算，消去感应数低阶项，提取感应数高阶项中的电阻率信息，从而达到提高频率电磁法近区测深能力和分辨率的目的。

本文基于王庆乙（2022）提出的两种广域电磁法 E-Ex 模式近区近区双频测深方案，通过模拟计算分析，论证了该方案的可行性，并指出了实际应用的关键因素。

1 电场近区双频测深理论

空间直角坐标系下，均匀半空间表面谐变电偶极子的电场 x 分量表达式为（汤井田和何继善， 2005）：

式（1）中，E_x为与电偶极子偶极矩方向相同的电场水平分量，r为接收点到偶极中心矢径的模，ϕ为r 和 x 轴的夹角。I 是电流强度，dL 是偶极子长度。ρ 和μ是均匀半空间的电阻率和导磁率，ω为角频率， k 为电磁波的波数，忽略位移电流影响时 k² = iωμ/ρ，$i=\sqrt{-1}$。

可将式（1）分解为传导电流产生的电场$E_x^c（r）$和感应电流产生的电场$E_x^i（r，\omega ）$两个部分，

其中，$E_x^c（r）=\frac{IdL}{2\pi r^3}\rho \left(3{\mathrm{c}\mathrm{o}\mathrm{s}}^2\varphi -2\right)，E_x^i（r，\omega ）=\frac{IdL}{2\pi r^3}\rho e^{-ikr}（1+ikr）$.

显然，水平电偶源激发电场的频率测深能力来自于感应电场$E_x^i（r，\omega ）$项。

分析式（1）、（2）可知，“ikr”项是表征电磁场传播的重要参数。事实上，该参数可以用感应数（或称为电距离）p = ikr/（i-1）进行表示（汤井田和何继善，2005）。当 p<<1，即电距离“近”时的区域称为 “近区”；当 p>>1，即电距离“远”时的区域称为“远区”；而当p≈1时，电距离介于前两者之间，称为过渡区。近区（p<<1）时的频率测深信息提取即为本文将探讨的问题。

将 p 代入$E_x^i（r，\omega ）$的表达式中并展开其中的超越函数项可得：

由于传导电流产生的电场$E_x^c（r）$仅有实分量，故式（2）所示的观测总场 E_x（r，ω）的虚分量等于感应电场$E_x^i（r，\omega ）$的虚分量，

不难推知，在近区条件下，如 p ≪ 1，可忽略上式中感应数的高次项，利用低阶近似式从观测总场的虚分量中提取具有频率测深能力的视电阻率。

Kaufman and Keller（1983）提出双频测深设想，通过双频测量和计算，设法消去几何测深项、突出感应测深项，以实现近区测深。王庆乙（2022）提出了两种广域电磁法近区视电阻率计算方案。方案一保留感应数 p 的低阶项（以下简称低阶方案），忽略式（4）中p⁵ 及以上的高阶项，取，

由 $k=（1+i）\sqrt{\mu \omega /2\rho }$ 可得，感应数$p=ikr/（i-\text{1）}=r\sqrt{\omega \mu /2\rho }$，代入上式并作变换可获得：

方案二保留式（4）中 p⁵ 相关项（以下简称高阶方案），忽略更高阶次项，取，

替换p并作变换可定义，

王庆乙（2022）认为相较于低阶方案（方案一），高阶方案（方案二）中依据观测数据所得视电阻率的阶次更高，因此依据高阶方案获得的视电阻率可获得更高的近区分辨率。

需说明，以上双频测深的视电阻率是从电场的虚分量中定义的。实际中，通过对实测电场信号进行傅里叶变换求取功率谱，并对功率谱数据进行叠加平均，即可获得复数域电场值，进而获得电场虚分量值，并计算相应的视电阻率值。

2 可行性论证

一维水平层状介质模型的偶极子场存在解析解（汤井田和何继善，2005），便于进行理论和计算分析。因此以下采用一维模型进行数值模拟，论证上述视电阻率计算方案的可行性。本文采用基于加权平均外推的 Hankel 变换算法（皇祥宇，2022），对水平层状介质表面谐变电偶极子场进行高精度计算。

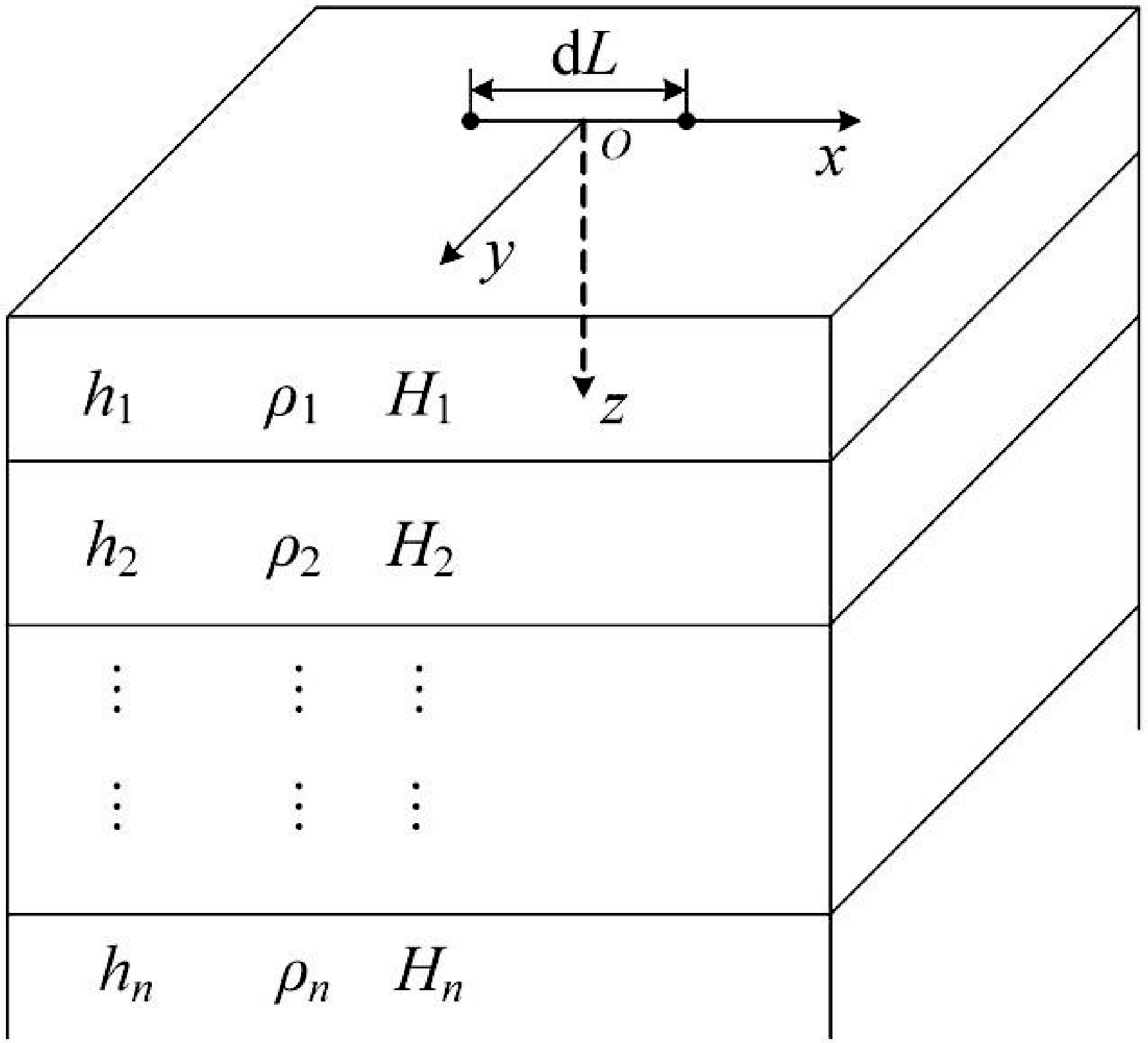
以下计算采用如图1 所示模型，N 层水平层状介质中第 n 层的电阻率和层厚度分别记为 ρ_n和 h_n （n=1，2，3. . .），Hn表示上覆盖层总厚度。一水平电偶极子（接地导线）位于层状介质表面，偶极矩为P= IdL（I为谐变电流，dL为偶极子的长度）。选取公共坐标原点位于偶极子中心的柱坐标系和直角坐标系，使 x轴指向偶极矩方向（即 ϕ = 0的方向，ϕ为观测点与偶极子连线方向的夹角），y轴垂直偶极矩方向，z轴垂直向下。

2.1 有限长导线的影响分析

理论部分推导的视电阻率是基于水平电偶极子场源获得的。然而实际中，开展近区测量时，接地偶极子的导线长度与发收距、测量深度等相比，已难以忽略，必须考虑导线长度对近区响应计算结果的影响。采用高斯积分方法（皇祥宇，2022）来获得长导线场源所产的场，并进行相应的视电阻率计算。

图2 中给出了两层模型 E-Ex 模式有限场导线源与偶极子源的电场分量及视电阻率响应计算结果对比。可以看出，有限长导线源主要影响电场总场和电场实部，而对电场虚部影响较小，因而对由电场虚部定义的视电阻率影响也较小。如图中所示的由低阶方案视电阻率在偶极子和有限长导线两种计算方式下结果相当。因此，对于电场近区双频测深方案，基于电偶极子的一些理论推导认识在实际的有限长导线条件下仍然成立，理论推导可以为实际应用提供参考。

需说明，本节各图的图例中，符号“p3”、“p5”分别表示与低阶方案、高阶方案相对应的变量。

2.2 不同场成分的强度对比

从前述理论分析中可知，广域电磁法 E-Ex 模式近区双频测深的能力来自于电场中的虚分量成分。因此不难推知，电场虚分量成分的强度大小将是决定前述近区双频测深方案的关键因素。为此，图3 给出了典型均匀半空间模型 E-Ex 模式电场中不同成分的强度随感应数变化的关系。可以看到： （1）近区内，实分量成分接近常数，几乎不随感应数改变而变化；虚分量成分的强度随感应数减小而减小；理论上电场实分量成分无法进行近区频率测深，而虚分量成分具备近区频率测深的条件。（2）虚分量成分在过渡区（p ≈ 1附近）范围内有极大值；在远区（p ≫ 1）随感应数增大震荡衰减，在近区 （p ≪ 1）随感应数减小单调衰减。（3）在感应数的整个变化范围内，电场虚分量成分的强度均小于实分量成分，电场总场中实分量成分占主导；虚分量与实分量的比值在过渡区内相对较大，极大值接近于 1；在 0.2 <p <3的范围内，虚分量与实分量的比值大于0.1，理论上具备可被分辨的条件。（4）近区内，电场虚分量的组成成分中，感应数的低阶项占主导，高阶项的比重随感应数减小而减小；并且阶数越高，其强度越小；其中3阶成分在0.2 <p <1的条件下、5 阶成分在 0.8 <p <1 的条件下与虚分量总场强度的比值大于 0.1。（5）远区内，电场虚分量各组成成分存在异号现象，导致电场虚分量总强度随感应数增大而急剧减小。

a—Ex总场对比；b—实分量对比；c—虚分量对比；d—视电阻率对比；计算条件：两层模型，h₁ = 1 km，ρ₁ = 100 Ω·m，ρ₂ = 10 Ω·m，r = 1 km， ϕ = 60°；|E_x |、|Re（E_x）|及|Im（E_x）|分别表示E_x总场、实分量及虚分量的绝对值；ρ_s表示视电阻率，“*-DP”表示偶极子源计算结果，“*-FL”表示有限场导线源计算结果；图d中2条视电阻率曲线基本重合

由图3 可推知，电场虚分量成分具有随感应数 （频率）变化的能力，这是进行近区频率测深的基本前提。前述近区双频测深的低阶方案计算的视电阻率虽然阶数低、可能对地下介质变化不够灵敏，但从低阶成分的可观测强度来看，应更具观测可行性。而高阶方案需要获取极弱的感应数高阶成分，对数据观测精度必然有极高的要求。

a—电场不同分量的强度；b—电场虚成分与实分量强度的比值；c—电场虚分量中不同成分的强度；d—电场虚成分各成分与虚分量强度的比值半空间模型电阻率为100 Ω·m，|E_x |、|Re（E_x）|及|Im（E_x）|分别表示E_x总场、实分量及虚分量的绝对值；|Im（E_x）-p²|、|Im（E_x）-p³|及|Im（E_x）-p⁵| 分别表示E_x虚分量中p²、p³及p⁵各项成分的绝对值

2.3 典型模型的视电阻率计算

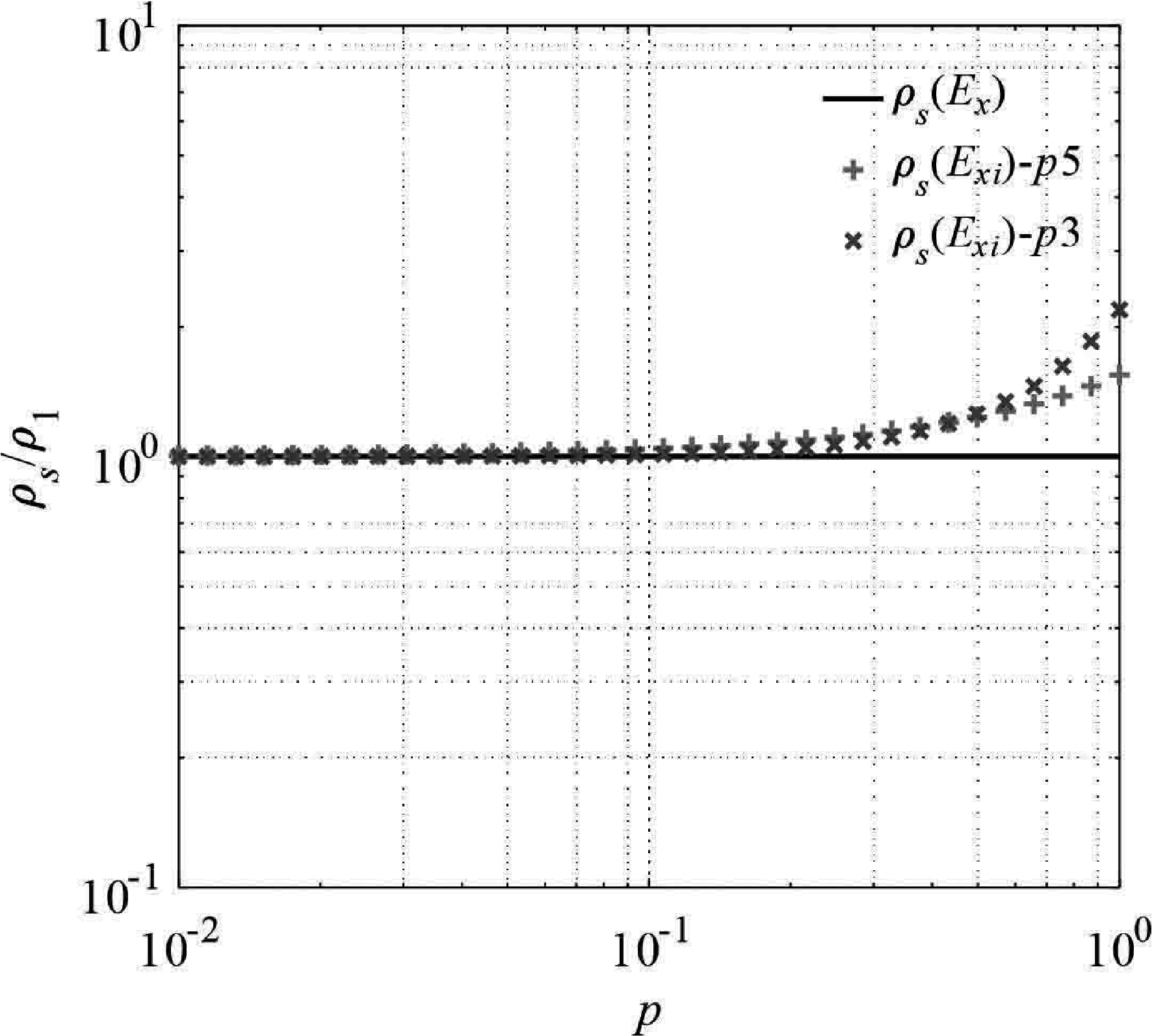
为更为明确的测试前述电场近区双频测深方案的效果，选择典型层状介质模型进行视电阻率计算。图4中给出了均匀半空间模型不同视电阻率定义方案的计算结果。可以看出，均匀半空间条件下，基于Ex总场定义的广域视电阻率在全区可获得半空间电阻率估计，而近区双频测深高阶方案及低阶方案定义的视电阻率仅在 p <0.1 的小感应数条件下才有效，在 p >0.1的范围内，高阶方案及低阶方案定义的视电阻率出现畸变，并且畸变程度随着 p 值增大而增大。这表明，电场近区双频测深方案仅在近区小感应数条件下才能获得相对可靠的理论计算结果，在过渡区内不具备显式频率测深能力。

ρ_s（ E_x）、ρ_s（ E_xi）-p5及ρ_s（ E_xi）-p3分别表示E_x总场、高阶方案及低阶方案定义的广域视电阻率

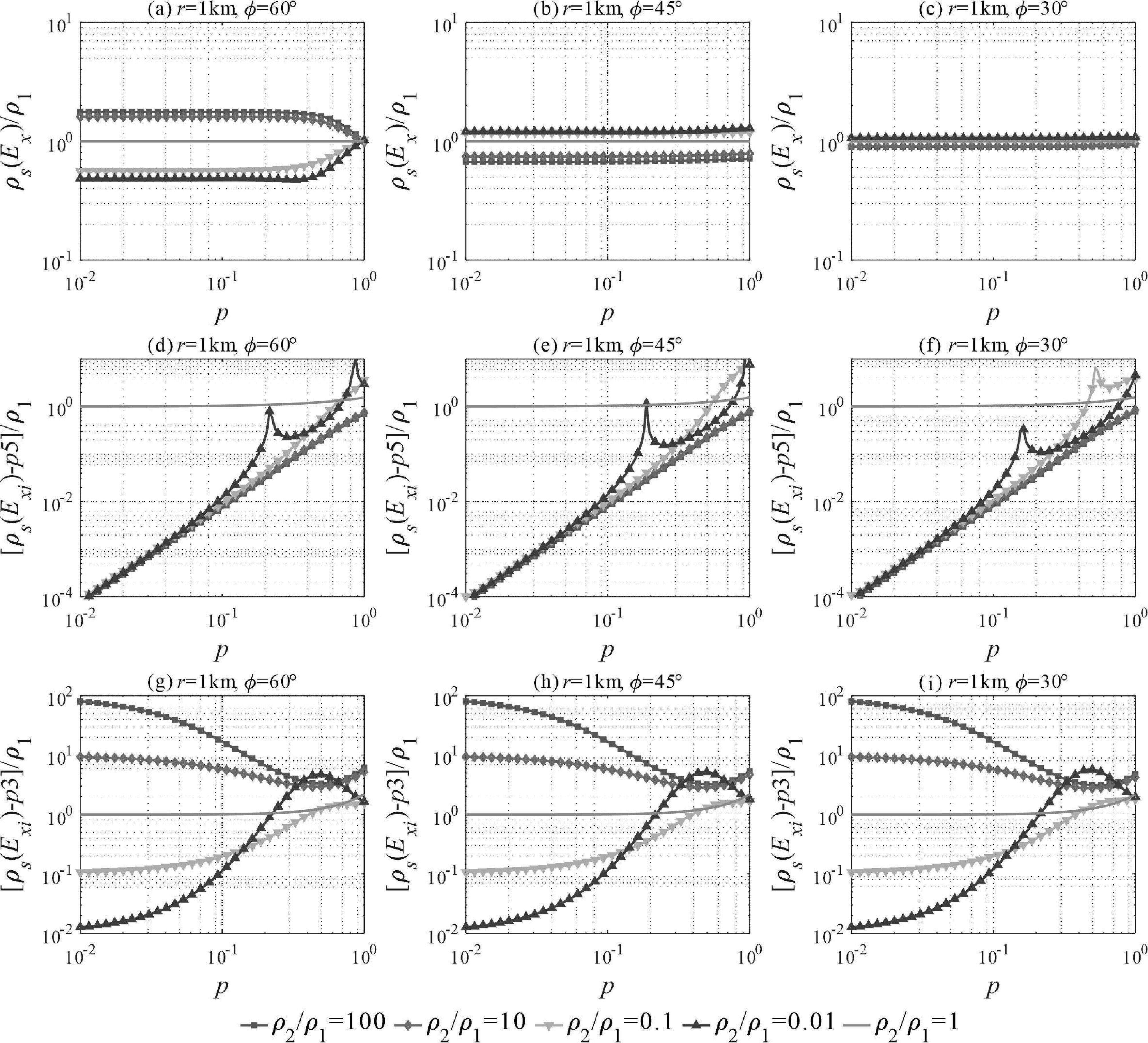
图5和图6中给出了两层模型不同视电阻率定义方案的计算结果，图5 给出了几组不同角度条件的对比，图6 给出了几组不同发收距条件的对比。可以看出，两层介质条件下，（1）基于Ex总场定义的广域视电阻率在p → 1的过渡区范围内有一定的频率测深能力，而在近区趋于稳定，不随感应数（频率）变化；视电阻率值与观测角度、发收距关系密切，仅在部分方位能够获取随感应数（频率）变化的信息。（2）双频测深高阶方案定义的视电阻率在两层介质条件下随感应数（频率）变化，在过渡区内对低阻基底的响应灵敏度高于高阻基底，但视电阻率曲线复杂，且与观测角度、发收距相关，不具备显式反映地电介质电阻率的能力。（3）双频测深低阶方案定义的视电阻率在两层介质条件下随感应数（频率）变化，在近区内对不同电性的高阻、低阻基底均有明显的响应灵敏度；视电阻率曲线对观测角度的变化不敏感、而随发收距变化，在过渡区相对复杂，而在近区意义明确，随着感应数的减小逐步收敛至基底电阻率真值。

两层模型，h₁ = 1 km，ρ₁ = 100 Ω·m，其它参数见子图名；（a、d、g）、（b、e、h）及（c、f、i）不同子图中观测角度分别为60°、45°及30°；（a、b、c）、（d、 e、f）及（g、h、i）分别为ρ_s（ E_x）、ρ_s（ E_xi）-p5及ρ_s（ E_xi）-p3的计算结果，其意义与图4相同

两层模型，h₁ = 1 km，ρ₁ = 100 Ω·m，其它参数见子图名；（a、d、g）、（b、e、h）及（c、f、i）不同子图中测量发收距分别为0.5 km、1 km及2 km；（a、 b、c）、（d、e、f）及（g、h、i）分别为ρ_s（ E_x）、ρ_s（ E_xi）-p5及ρ_s（ E_xi）-p3的计算结果，其意义与图5相同

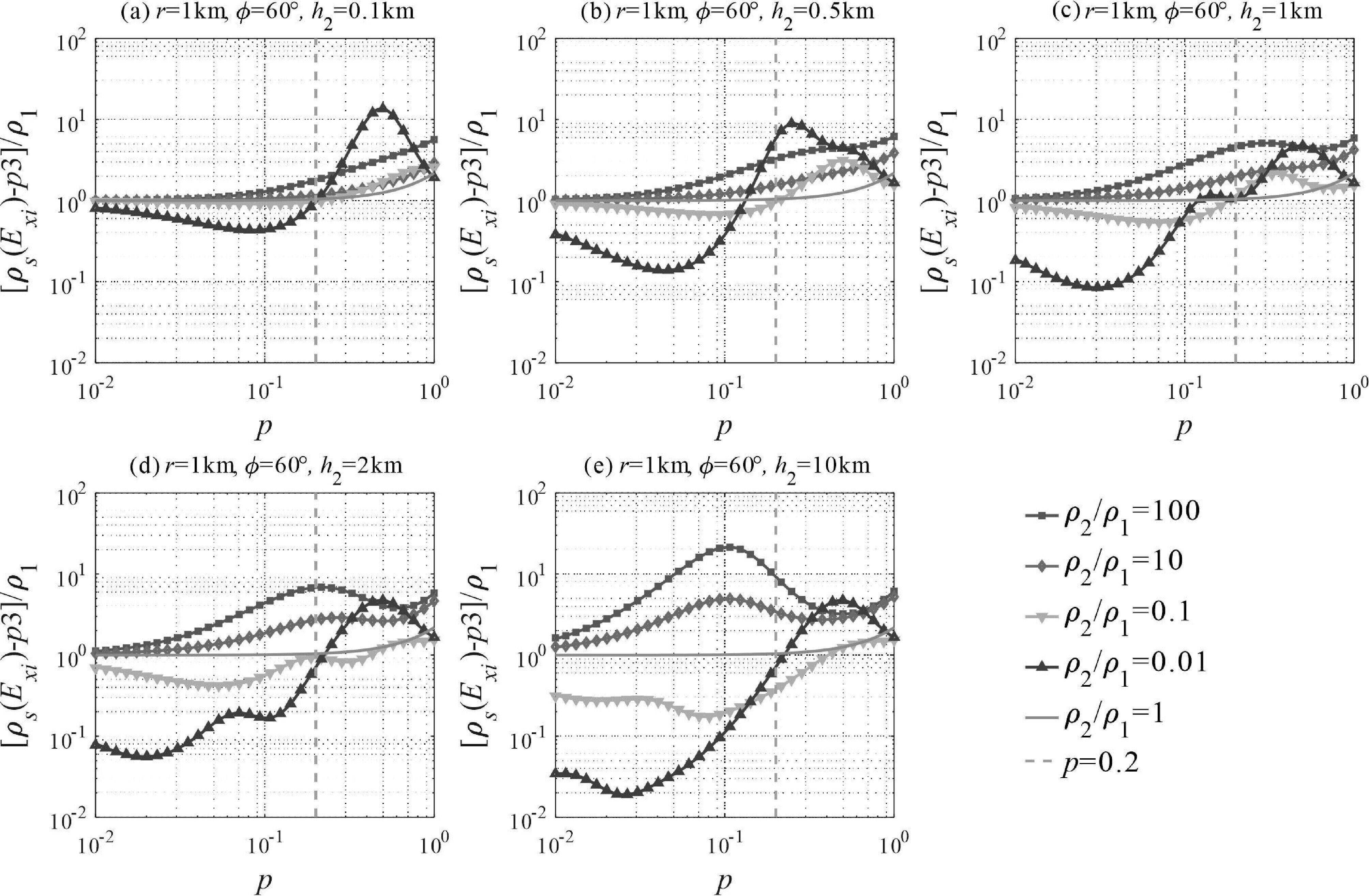
图7和图8中给出了三层模型不同视电阻率定义方案的计算结果，图7 给出了几组不同发收距条件的对比，图8 给出了几组不同中间层厚度条件的对比。可以看出，三层介质条件下，（1）Ex总场广域视电阻率总体规律与图5、图6所示的两层介质条件类似；（2）低阶方案视电阻率在近区内对不同电性的中间层介质均有明显的响应灵敏度；视电阻率曲线难以显式反映首层介质电阻率真值，但在近区随着感应数的减小能够逐步收敛至基底电阻率真值。 （3）低阶方案视电阻率随发收距改变而变化，但总体形态类似；该视电阻率对中间层厚度及电性变化的响应敏感，中间层厚度越大，电性差异与盖层/基底越大，响应越明显。（4）与两层介质条件下的认识类似，高阶方案定义的视电阻率对地电参数变化具有一定的响应灵敏度，但视电阻率曲线复杂，不具备显式反映地电介质电阻率的能力。

值得指出，尽管近区双频测深高阶、低阶方案定义的视电阻率未必能显式反映地下介质电阻率真值的变化，但只要能获得相应介质变化的响应，则有可能在后续通过反演等手段揭示地电模型真值。

三层模型，h₁ = h₂ = 1 km，ρ₁ = ρ₃ = 100 Ω·m，其他参数见子图名；（a、d、g）、（b、e、h）及（c、f、i）不同子图中测量发收距分别为0.5 km、1 km及2 km；（a、b、c）、（d、e、f）及（g、h、i）分别为ρ_s（ E_x）、ρ_s（ E_xi）-p5及ρ_s（ E_xi）-p3，其意义与图4相同

综合来看，理论上与总场和高阶方案相比，电场双频测深低阶方案具有最佳的近区频率测深能力。

2.4 频率间隔的影响分析

本文所述的双频测深方案的理论基础是通过双频测量和计算，达到近区频率测深的目的。因此，双频的频率间隔是本方法必须考虑的影响因素。图9 中给出了两层模型 E-Ex 模式稀疏频率密度条件双频低阶方案视电阻率的计算结果。图9中感应数每个数量级含 5 个数值（频率），而图6 中感应数每个数量级含50个数值（频率）。对比可知，频率间隔对双频低阶方案计算结果的影响不大。考虑到当前广域电磁法实际应用中已可进行伪随机 39频激发，且每个数量级可发 10个左右频点，现有的发送频率密度已完全满足本文所述方案的计算需求。

三层模型，h₁ = 1 km，ρ₁ = ρ₃ = 100 Ω·m，其他参数见子图名；各子图中，第二层厚度h₂分别为0.1 km、0.5 km、1 km、2 km、10 km，其他参数相同

感应数每个数量级含5个数值（频率），而图5中感应数每个数量级含50个数值（频率）；a、b及c不同子图中测量发收距分别为0.5 km、1 km及 2 km；其他计算条件与图5相同

2.5 误差的影响分析

如前文场强度分析部分所述，基于电场虚分量观测的双频测深方案的最大难题为信号测量精度。为测试数据误差对视电阻率计算结果的影响，本节考虑给理论观测数据加入一定比例的随机扰动，模拟观测噪声的影响。图10 中给出了均匀半空间模型 E-Ex模式含扰动条件下电场强度及视电阻率计算结果，其中给电场虚分量添加1‰比例的扰动量。由图10可知，尽管 1‰ 比例的扰动量对电场虚分量强度的绝对值影响不大，但对双频测深视电阻率值的影响已十分显著，将导致视电阻率计算失效。事实上，由于近区内感应数的高阶项随感应数减小而快速衰减，电场虚分量合成值中的扰动量强度已显著超过其中的相对高阶成分。由于双频测深方案需要使用感应数的相对高阶成分（与 p³、p⁵ 有关的项），因此双频测深视电阻率将极大受观测误差或噪声等因素影响。这表明，对于基于电场虚分量观测和计算的频率测深方案，信号的测量精度至关重要。

a—场分量强度分析；b—虚分量成分分析；c—含扰动信号的视电阻率电场虚分量的扰动量为1‰；“*+error”表示含扰动数据，“error”表示扰动量，其他条件及符号与图3和图4所示相同

3 结论

本文探讨了两种广域电磁法 E-Ex 模式近区双频测深方案的可行性。获得以下认识：

（1）基于Ex总场定义的广域视电阻率在近区基本不随感应数（频率）变化，不具备频率测深能力。

（2）E-Ex模式双频测深高阶方案定义的视电阻率在过渡区内和近区内对低阻层的响应灵敏度高于高阻层，但视电阻率曲线复杂，无法显式反映地电介质真实电阻率的变化。

（3）E-Ex模式双频测深低阶方案在理想条件下可以获得近区地电介质随频率的变化信息，受观测角度、接地导线偶极长度及观测频率间隔等因素影响均较小，具备实现频率测深的可能性。然而，该方案对观测数据误差极为敏感，观测总场中较小的误差也将导致近区视电阻率信息提取失败。

综上，笔者认为，广域电磁法 E-Ex 模式电场近区双频测深方案实际应用的关键在于控制观测精度。电场虚分量成分具有随感应数（频率）变化的能力，如何更合理地挖掘其中蕴含的频率测深信息值得更进一步的研究，探索更合理的信息提取方案。

注释

① McNeill J， Bosnar M.1999. Technical Note TN-31： Application of ‘Dipole-Dipole’Electromagnetic Systems for Geological Depth Sounding[R]. Ontario： Geonics Limited.

参考文献