-
0 引言
-
地学数据采集受多种客观因素的影响,采集的数据点在平面上常常呈离散且不规则分布特征,为便于对数据进行绘图和分析,通常利用空间插值方法将离散数据加密,并形成规则分布的空间数据点集。空间插值方法的种类较多(如克里金法、最小曲率法、径向基函数法、自然邻点法、反距离加权法等),它们在插值准确性、视觉呈现、参数敏感性以及耗费时间和内存等方面各有优缺点(Franke, 1982;Myers,1994)。
-
本文将趋势面函数与多重二次曲面函数融合构建复合数学曲面,用于解决平面离散数据的建模问题。趋势面函数作为趋势分析的工具被广泛应用于地学和工程数据分析,例如统计分析大气降水 (Edwards,1973)、生态学数据分析(Gittins,1968)、分析瓦斯气体分布(Tong et al.,2015)、河流网络提取(Su,2020)、三维喀斯特系统建模(Gao and Lin, 2020)等。多重二次曲面函数具有良好的保形性和单调性,已被广泛用于大地测量学、地球物理学、气象学、水文学、计算科学等领域(Hardy,1971, 1978①,1990)。Pegram and Pegram(1993)根据雨量计观测数据,采用多重二次曲面函数估算区域性降雨量,计算结果可靠性较好。Martens et al.(2013) 基于雨量计和天气雷达的实时观测数据,提出了一种快速估算区域性降雨量的自适应多重二次曲面拟合法,使得降雨量的计算具有实时性。芮小平等 (2000)利用多重二次曲面函数构建煤层底板标高模型,计算结果表明该方法对不规则连续曲面具有良好的逼近效果。Song et al.(2010)通过对多重二次曲面函数施加一阶和二阶粗糙度惩罚约束,使得构建的地质界面模型更加光滑流畅,通过改善形状参数或施加约束可以改善多重二次曲面函数的建模效果(Song et al.,2010;Martens et al.,2013),除此而外,通过与其他方法结合也可以改善多重二次曲面法的建模效果。张菊清和刘平芝(2008)将抗差趋势面与正交多重二次曲面函数结合,实现了地表高程数据的光滑建模。赵仕威等(2017)将反距离加权法与多重二次曲面函数结合,实现了稀疏钻孔数据的地层界面重构。总体而言,上述多重二次曲面法主要适合于小规模数据体建模,而对于海量数据的高效光滑建模,多重二次曲面法仍然具有一定的研究空间。
-
趋势面函数能较好地反映离散数据集的全局特征,但局部特征信息容易被压制。多重二次曲面函数能较好地反映离散数据集的局部特征信息,但容易因离散点集分布不均匀而使曲面产生畸变。因此本文将两者结合构建空间数学曲面,使其能够准确逼近离散数据集的空间起伏变化特征。本文首先简要介绍趋势面函数与多重二次曲面函数在数据分析中的基本原理,然后介绍融合趋势面函数的多重二次曲面插值方法,最后对模型数据、高程数据、磁法图形数字化数据进行二维插值,测试算法的数据恢复质量。
-
1 融合趋势面函数的多重二次曲面法
-
1.1 趋势面函数
-
根据离散数据点 pi( xi,yi,zi)(i = 1,2,···,M),可构造出反映离散点全局特征的趋势面函数T( x,y):
-
式(1)中,n 为趋势面阶数,n 取值越大,在数据分布相对密集且均匀的区域,趋势面对离散数据逼近程度越高,而在数据缺失区趋势面容易形成震荡 (刘海飞等,2021)。cij 为趋势面系数,其个数 N =(n + 1)(n + 2)/2。
-
为确定趋势面系数 cij,需要将离散点 pi( xi,yi,zi)(i = 1,2,···,M)代入方程(1),并令 T( xi,yi)= zi,可得线性方程组:
-
其中方程个数 M 通常远远大于趋势面系数的个数N。方程(2)为超定方程组,需要在最小二乘意义下对其求解,若令 R = AC-Z,使取极小,得
-
该方程可采用全选主元高斯消去法进行求解,即可得到趋势面系数C,将其代入式(1)便可得到趋势面函数。
-
1.2 多重二次曲面函数(MQ)
-
根据数据点 pi( xi,yi,zi)(i = 1,2,···,M),可构造出反映数据点局部特征的多重二次曲面函数 Q( x,y):
-
式(2)中,q( xi,yi,x,y)为二次曲面函数,wi为二次曲面系数,s为形状参数,用于调节二次曲面的平滑度,其值越大曲面越平滑。
-
关于形状参数 s 的选取问题,Hardy(1971)将 s 定义为,其中di是第i个数据点与其最近邻点之间的距离。Franke(1982)给出选取 s 的经验公式,D为包含所有数据点的最小外接圆的直径,但在实际应用中发现,按该公式选取形状参数有时导致多重二次曲面过于平滑,因此本文采用 。目前关于形状参数 s 的选择多为经验公式,在小计算量下未见最优选取方法,主要由于其值与数据点的数量和分布以及数据的起伏变化及观测精度有关(Rippa,1999)。在建模中,为保证构建的数学曲面尽量逼近真实曲面,形状参数s通常取较小的值。
-
为确定二次曲面系数 wi,需要将离散点 pi( xi,yi,zi)(i = 1,2,···,M)代入方程(4),并令 Q( xi,yi)= zi,可得线性方程组
-
其中
-
求解方程(5)可得到多重二次曲面系数W,然后将其代入方程(4),便可得到多重二次曲面函数。从线性方程(5)中不难看出,矩阵 AM × M 的元素均是由数据点之间的平面距离构成的,其性态往往受数据点的分布特征的影响,数据点分布越均匀其病态程度越小,采用全选主元高斯消去法求解方程(5),即可得到较优的权系数(刘海飞等,2021)。
-
1.3 趋势面函数与多重二次曲面函数融合
-
上述趋势面函数 T( x,y)能较好地反映离散数据集的全局特征,但局部特征信息容易被压制。多重二次曲面函数 Q( x,y)能较好地反映离散数据集的局部特征信息,但容易因离散点集分布不均匀或缺失使曲面产生畸变。因此本文将两者结合构建空间数学曲面H( x,y),使其能够准确逼近离散数据集的空间起伏变化特征。
-
将趋势面函数 T( x,y)与多重二次曲面函数 Q( x,y)叠加构建复合曲面函数H( x,y):
-
式(6)中,趋势面函数 是利用数据点 pi( xi,yi,zi),i = 1,2,···,M 按式(1)构建,而全局多重二次曲面函数是利用数据点 pi( xi,yi,zi-T( xi,yi)),i = 1,2,···,M 按式(4) 构建。两者在平面坐标( xi,yi),i = 1,2,···,M 所确定的最大矩形区域x ∈ [ xmin,xmax ]且y ∈ [ ymin,ymax ]上叠加,便可得到复合曲面函数 H( x,y),这里将该算法简记为 MQT(multiquatric surface combining with trend surface)。
-
2 数值对比实验
-
2.1 模型数据分析
-
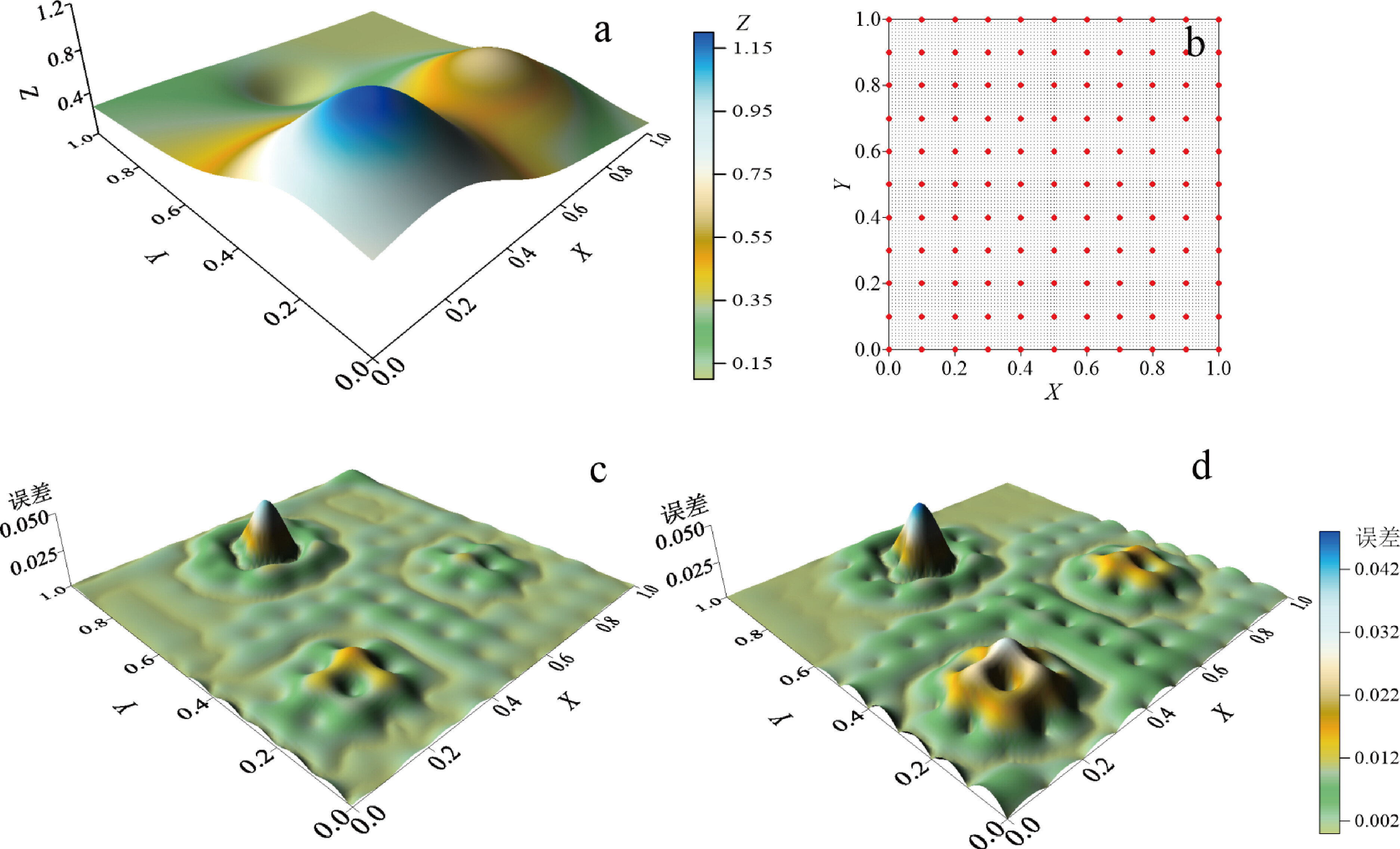
为对比分析融合趋势面函数的多重二次曲面法MQT的数据恢复精度,选择函数:
-
作为实验函数(Franke,1982),该函数的曲面形态如图1a 所示。首先以步长 0.1 在区域 0 ≤ x ≤ 1 且 0 ≤ y ≤ 1 上沿 x,y 方向均匀剖分,获取的数据点为 121个(图1b中圆点为点位分布),然后将该组数据作为已知点,并以步长 0. 01 在区域 0 ≤ x ≤ 1 且 0 ≤ y ≤ 1 上沿 x,y 方向均匀离散的坐标点( x,y)作为未知点(10201 个),再利用 MQT 及克里金法预测未知点上的近似函数值,并计算其与函数 f ( x,y)精确解的绝对误差,以此对比分析 2 种方法的数据恢复精度。
-
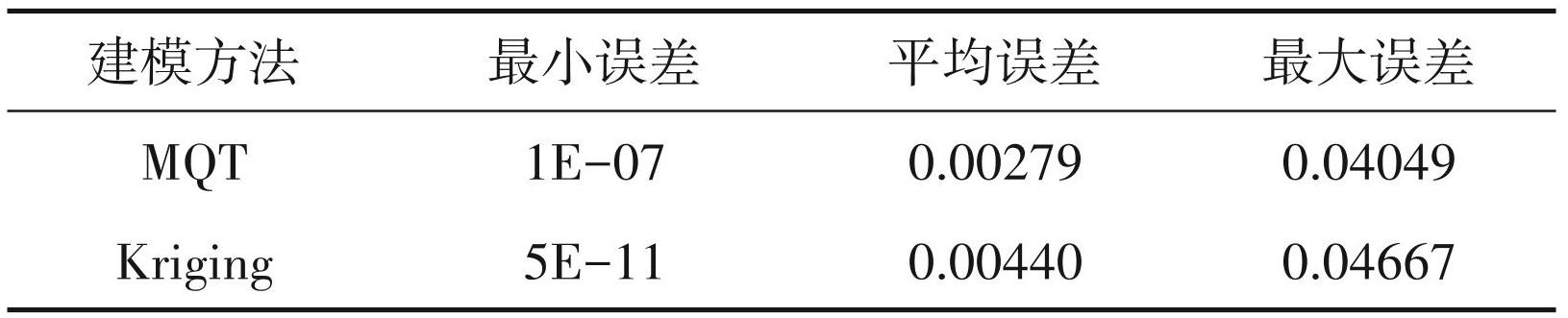
从 MQT 法恢复结果的误差(图1c)和克里金法 (Kriging)恢复结果的误差(图1d)可以看出两者的误差形态相近,误差主要集中于函数峰值附近,结合误差统计表(表1),MQT 法的最大和平均误差略小于克里金法,特别是在函数峰值区域,而在相对平坦区域,克里金法的精度要高于MQT法。
-
2.2 高程数据的恢复结果分析
-
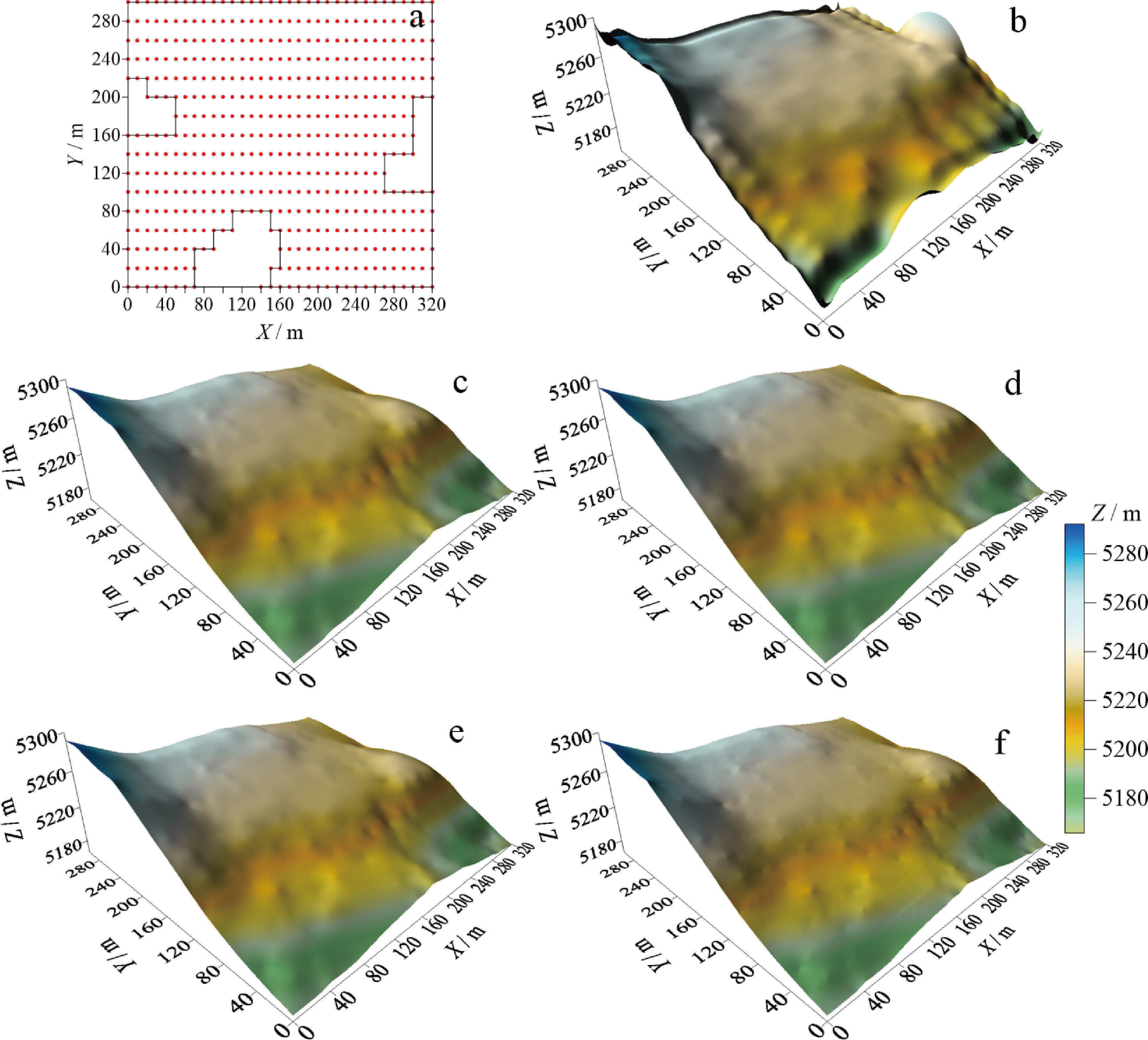
选择西藏某地采集的地表高程数据进行数值实验分析,数据点数 488个,点位分布如图2a所示,其中 X 方向长度 320 m,点距 10 m,Y 方向长度 300 m,点距 20 m,部分区域有数据缺失。对该数据区 (320 m×300 m)按正方形单元(1.6 m×1.6 m)进行剖分,X、Y 方向的节点数分别为 201 和 188,分别采用不同阶数的趋势面函数法、多重二次曲面函数法、MQT 法以及克里金法恢复地形表面,结果如图2b~f所示。
-
图1 模型数据的恢复结果
-
a—实验函数的曲面形态;b—数据点分布;c—MQT法的误差;d—克里金法的误差
-
图2 融合不同阶次趋势面函数的多重二次曲面法的结果
-
a—已知数据点的分布图;b—多重二次曲面法的结果;c—融合一阶趋势面函数的多重二次曲面法的结果;d—融合二阶趋势面函数的多重二次曲面法的结果;e—融合三阶趋势面函数的全局多重二次曲面法的结果;f—克里金法的结果
-
采用 1.2 节多重二次曲面函数法(未融合趋势面函数),对起伏地表高程的恢复结果如图2b所示,可以看出在数据缺失区和数据边界附近均出现了不同程度的畸变。而采用1.3节融合趋势面函数的多重二次曲面法的恢复结果如图2c~e所示,可以看出构建的复合曲面平滑、流畅,数据缺失区的畸变效应得到了较好地压制,说明两者结合在改善建模质量上是非常有效的。对比图2c和图2e,可以看出融合不同阶次的趋势面函数对多重二次曲面的恢复结果影响较小,在数据特征起伏变化不大的情况,为减少建模计算量,尽量选择低阶趋势面函数与多重二次曲面函数融合。融合趋势面函数的多重二次曲面法的结果与克里金法的结果(图2f)相比,在数据缺失区两者融合的复合曲面的趋势性略优。
-
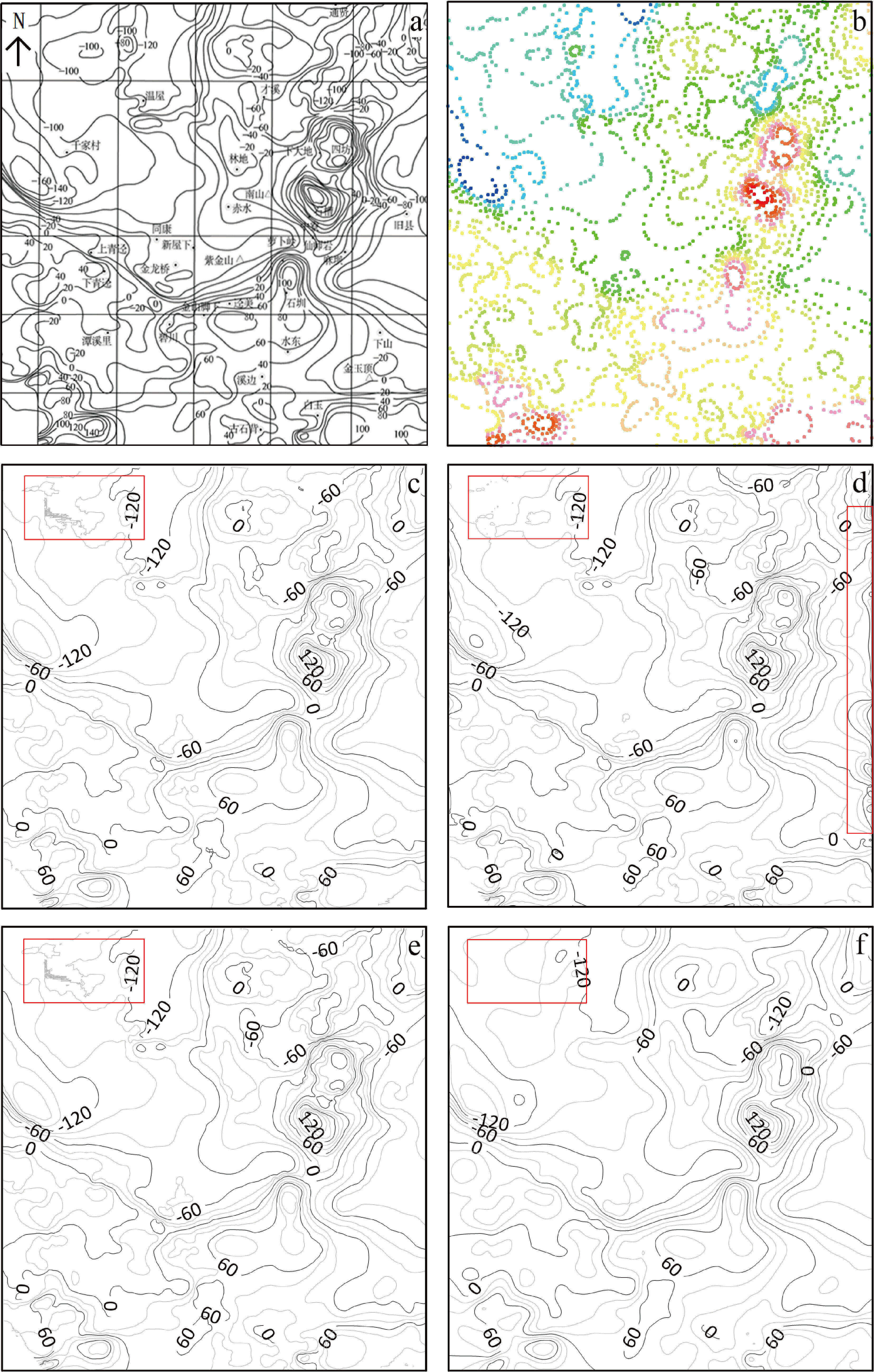
图3 不同方法磁法数据的恢复结果
-
a—原始磁法数据等值线图;b—数字化的离散点;c—克里金法的结果;d—最小曲率法的结果;e—径向基函数法的结果;f—MQT法的结果
-
2.3 图形数字化的磁法数据恢复结果分析
-
以某地区磁法数据为例进行数值实验分析,磁法等值线图如图3a所示,数字化后的离散点分布如图3b 所示,离散数据点个数 18725 个,从图中可以看出,数据点分布非常不均匀。采用对该数据区 (22000 m×23000 m)按矩形单元(11. 0 m×11.5 m) 进行剖分,X、Y 方向的节点数分别为 2000 和 2000,采用克里金法、最小曲率法、径向基函数法(局部多重二次曲面函数法)及本文融合趋势面函数的多重二次曲面法,重新恢复磁法等值线数字化数据,恢复结果分别如图3c~f所示。可以看出,几种方法基本可以恢复原有等值线形态,但在离散点比较稀疏的区域均有一些畸变,如图中红色矩形框。相对其他方法,本文 MQT 方法得到的等值线形态总体光滑,能够压制离散数据中局部畸变的影响。
-
3 结论
-
本文通过对融合趋势面函数的多重二次曲面建模方法的研究,得到以下几点认识:
-
(1)采用等值线图数字化的数据具有强烈的不均匀性特征,采用本文MQT方法可以获取光滑的网格化数据,能够为后续进一步数据处理奠定基础。
-
(2)将趋势面函数与多重二次曲面函数融合,联合构建空间数据场模型,相较于其他单一的网格化方法,可有效降低因部分区域数据缺失而产生的畸变效应。对于趋势面函数的阶次,选择 1~3 阶较宜。
-
(3)对于趋势面函数与多重二次曲面函数融合的网格化方法 MQT,更适合于小规模数据体(<10000)建模,可以在短时间内(<60 s)构造出反映数据全局特征的光滑曲面。
-
注释
-
① Hardy R L.1978. The Application of Multiquadric Equations and Point Mass Anomaly Models to Crustal Movement Studies[R]. Bouder: NOAA.
-
参考文献
-
Edwards K A. 1973. Estimating areal rainfall by fitting surfaces to irregularly spaced data[C]// Proc of the International Symposium on the Distribution of Precipitation in Mountainous Areas.
-
Franke B R. 1982. Scattered data interpolation: Tests of some methods[J]. Mathematics of Computation, 38(1): 181‒200.
-
Gao J, Lin X. 2020. Mathematical interpolation and correction of Three-Dimensional Modelling of High-Speed Railway[J]. Intelligent Automation & Soft Computing, 26(5): 1023‒1034.
-
Gittins R. 1968. Trend-Surface analysis of ecological data[J]. Journal of Ecology, 56(3): 845‒869.
-
Hardy R L. 1971. Multiquadric equations of topography and other irregular surfaces[J]. Journal of Geophysical Research, 76(8): 1905‒1915.
-
Hardy R L. 1990. Theory and applications of the multiquadric-biharmonic method[J]. Computers & Mathematics with Applications, 19: 163‒208.
-
Martens B, Cabus P, De Jongh I, and Verhoest N E C. 2013. Merging weather radar observations with ground-based measurements of rainfall using an adaptive multiquadric surface fitting algorithm[J]. Journal of Hydrology, 500: 84‒96.
-
Myers D E. 1994. Spatial interpolation: An overview[J]. Geoderma, 62(1): 17‒28.
-
Pegram G C, Pegram G G S. 1993. Integration of rainfall via multiquadric surfaces over polygons[J]. Journal of Hydraulic Engineering, 119(2): 151‒163.
-
Rippa S. 1999. An algorithm for selecting a good value for the parameter c in radial basis function interpolation[J]. Advances in Computational Mathematics, 11(2/3): 193‒210.
-
Song X F, Rui X P, Ju Y W, Yang Y G. 2010. Improved geologic surface approximation using a multiquadric method with additional constraints[J]. Mining Science and Technology, 20(4): 600‒606.
-
Su D S. 2020. Study on the river network extraction method from complex surface based on trend surface fitting[C]//IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS).
-
Tong Z Y, Tong M M, Liu B, Li M. 2015. Research on gas emission distribution in coalface based on trend surface polynomial analysis[J]. IEEE Sensors Journal, 15(1): 164‒171.
-
刘海飞, 柳建新, 柳卓. 2021. 数值计算与程序设计(地球物理类)[M]. 长沙: 中南大学出版社.
-
芮小平, 余志伟, 许友志, 奚砚涛. 2000. 多重二次曲面插值法在地质曲面拟合中的应用[J]. 中国矿业大学学报, 29(4): 377‒380.
-
张菊清, 刘平芝. 2008. 抗差趋势面与正交多面函数结合拟合DEM数据[J]. 测绘学报, 37(4): 526‒530.
-
赵仕威, 周小文, 湛杰, 刘攀. 2017. 混合多重二次插值在三维地层可视化中的应用[J]. 地下空间与工程学报, 13(1): 161‒168.
-
摘要
为方便对一些老的纸质等值线图件进行数据再处理,首先需要对图件进行数字化,然后再进行二维网格化,网格化数据质量直接影响后续数据的处理效果。由于等值线图的数字化数据具有不均匀的特点,网格化后容易产生数据畸变的问题,本文提出了融合趋势面函数的多重二次曲面网格化方法。该方法首先根据已知离散点构建低阶趋势面函数,然后利用已知离散点与低阶趋势面函数的差构建多重二次曲面函数,再将低阶趋势面与多重二次曲面叠加构造出新曲面,两者结合可较好地消除多重二次曲面函数在数据稀疏区的畸变效应。通过对磁法等值线图数字化数据进行插值测试,验证了融合趋势面函数的多重二次曲面插值方法具有良好的保真性。
Abstract
In order to facilitate the reprocessing of older paper contour maps, it is necessary to digitize the maps first, followed by a two-dimensional grid generation, and the quality of this gridded data significantly influences subsequent data processing outcomes. Given the uneven nature of digitized data from contour maps, issues of data distortion often arise during grid generation. This paper introduces a method for grid generation that integrates global multiquadric (MQ) method with trend surface functions. The approach begins by constructing low-order trend surface functions based on known discrete points. Subsequently, it utilizes the difference between known discrete points and low-order trend surface functions to formulate a MQ function. This involves superimposing the low-order trend surface with the MQ function to create a novel surface. This method effectively mitigates the distortion effects of MQ function in data-sparse regions. Interpolation tests conducted on model data, elevation data and digitized data from magnetic contour maps validate the fidelity of this grid generation method, showcasing its effectiveness in preserving data accuracy.