0 引言

深埋巷道开挖过程中，由于围岩开挖引起的集中应力大于围岩强度，围岩受到损伤，逐渐出现裂纹，随着裂纹的进一步扩展，进而形成围岩松动圈，导致围岩失稳，给施工的安全性带来巨大的挑战。为了控制巷道围岩的稳定性，国内外学者进行了大量的研究。

Hill et al（.1966）首先提出能量释放率的概念，以及岩爆发生次数、规模及对采矿造成的损失。 Kanagalingam and Thevanayagam（2006）采用有限差分法来模拟能量耗散、孔隙压力的产生、孔隙水压力消散。朱维申和程峰（2000）、朱维申等（2001）基于能量耗散原理，建立了能量耗散本构模型，并在工程中进行了大量的应用。金丰年等（2004）基于材料的本构及耗散能，定义了材料的损伤，确定了损伤变量的计算公式，研究了损伤扩展规律。李铁等（2007）通过现场微震观测和工程数据分析，定量揭示了煤巷开采活动与矿震能量释放间的内在联系及力学机理。谢和平等（2004，2005）认为岩石在变形破坏过程中是一个能量耗散的损伤演化过程，并提出了基于能量耗散的强度丧失准则和基于可释放应变能的整体破坏准则。苏国韶等（2006）提出局部能量释放率新指标，并认为其可作为地下工程开挖方案的优化指标。王襄禹等（2010）基于应变软化准则建立了变形压力的力学模型，依据变形压力的变化规律分析了有控卸压机理，并提出了 “临界塑性区半径”作为有控卸压的判定准则。王伟等（2020）采用FLAC3D数值模拟及巷道围岩支护理论，研究了巷道分步开挖时及巷道支护完成后的稳定性。

综上所述，国内外学者基于能量耗散理论的作用机理、工程应用进行了大量的研究，大部分都是基于围岩体的能量耗散建立本构关系，然后对支护体系进行优化（宋大钊，2012；高速等，2015；张斌川，2015；张志镇和高峰，2015；丁向勇等，2022）。但是，对于无支护巷道最优半径的取值研究尚少。因此，基于能量耗散原理，进行无支护条件下巷道开挖最优半径的研究是非常有必要的。

1 巷道开挖引起的能量耗散与释放

根据热力学不可逆过程，任何能量的耗散与释放都不会自发的产生，都是在受到外界的影响下发生的，同时，能量应该遵循守恒定律（Cao et al.， 2006；Zhang et al.，2014）。

1.1 能量原理

设弹性体受到全部 6 个应力分量 σ_x、σ_y、σ_z、τ_yz、 τ_zx、τ_xy，6 个分量全部按照同样的比例增加，根据能量守恒定理，定量计算每个应力分量的比能并相加得到：

根据弹性力学本构关系：

式（2）中：E 是弹性模量，ν 是泊松比， G=E/2（1+ν）；

求解得到单位体积应变能为：

整体积分求得整个弹性体的形变势能：

1.2 应力场

在地下工程建设过程中，不论是煤巷，还是隧道工程，都不可避免的遇到围岩收敛，冒顶甚至塌方的危害，给施工人员的身命安全以及工程的稳定性带来潜在的威胁。这些危害的产生都受到地应力的影响，因此，研究地应力的分布规律对上述问题的解决具有重要的作用（Du et al.，2022；Huang et al.，2023；张文康等，2023）。

设有一围岩体无限大，围岩特点：均质各项同性且具有线弹性特点，不发生流变或无黏性行为，在巷道断面内，水平和竖直方向的原岩应力相等，且沿巷道长度方向是恒定的。假设巷道开挖断面为标准圆形，巷道长度无限长（实际工程中一般情况下其长度是有限的），巷道围岩的性质均匀且一致。因此可采用弹性理论中平面应变问题的求解方法进行计算，取巷道的任一截面作为代表性研究对象。巷道断面如图1所示。

设围岩体的埋深符合Z≥20R₀的深埋条件，其中 Z为巷道埋深（m），R₀为巷道半径（m）。大量的研究表明，当巷道埋深Z满足大于或等于20倍巷道半径时，可以忽略巷道影响范围（5R₀）内的岩石自重。因此，在满足上述假设的情况下，列出基本方程（平衡方程、几何方程以及本构方程），根据边界条件（无支护反力）求出解析解（蔡美峰，2002；张永杰， 2010；Yu and Yan，2014）。

式（5）中：P₀是竖向自重应力，r是小于等于巷道半径R₀的任意数值。

1.3 计算简化模型

为简化计算，进而基于巷道开挖中的能量耗散与释放以及开挖前后整体能量守恒原理（Chan et al.，2008；Yu and Yan，2014），根据巷道开挖引起围岩体中的应力重分布求解的应力场，提出如下基本假定：

（1）假定巷道开挖深度符合深埋条件：Z≥20R₀，巷道开挖之前围岩体是完整的（即无裂纹、无损伤） （图2）。

（2）假定巷道岩体均质弹性、各项同性以及满足小变形，满足弹性理论求解要求；

（3）假定巷道开挖过程中断面为理想圆形（图3）；

（4）忽略巷道顶部与底部之间的应力差，采用巷道断面中心距地表的距离作为埋深进行地应力的计算，其计算误差在深埋巷道工程应用中符合要求；

（5）忽略巷道开挖中人为造成的能量变化（如机械摩擦及重锤敲击等，其数量级较小，可以忽略不计），只考虑巷道开挖时爆破对整体能量的影响。

2 基于能量耗散原理的临界开挖半径

根据能量守恒原理，巷道开挖之前单元围岩体储存的弹性应变能应该与巷道开挖后单元围岩体所储存的能量相等（未考虑爆破的情况），即：

式（6）中：U₀为开挖前单位围岩体的能量，U₁为开挖后单元围岩体的能量，U₂为开挖后新增加的单元表面能，U₃为单元耗散能用于形成单元内部损伤、裂纹产生以及塑性变形。

同时式（6）两端进行积分，求得总能量之间的关系为：

式（7）中，围岩体的体积V可近似取半径为5R₀，计算长度为单位长度（B）的圆柱体进行积分计算；V₁ 取半径为R₀到5R₀及计算长度为单位长度的圆环体进行积分计算；S 近似取开挖长度为单位长度的开挖面进行积分计算（图4）。

类比损伤力学中损伤因子的定义，定义能量损伤因子为：

式（8）中：U_C为单元强度丧失时的临界能量耗散值，为材料常数，与应力状态无关，可通过岩石单轴拉、压与纯剪试验来确定。任意应力状态下，D=0 时，材料强度丧失，即：

将式（9）代入式（7）后，有：

式（10）为基于能量耗散的巷道岩体强度丧失准则。

为方便计算，在主应力空间中，巷道开挖之前围岩应力（原岩应力）为三轴等压状态，σ₁=σ₂=σ₃= P₀，而且围岩处于弹性变形阶段，代入式（3）求得：

将dν=2πBrdr代入式（11）得到：

求解（12）得：

巷道开挖之后，依据围岩应力场（式（5）），代入式（3）得到：

对式（14）两边同时积分得到：

将dν₁=2πBrdr代入式（15）得到：

求解式（16）得到：

根据表面能的定义，可知单位面积表面能为γ，设计算长度为单位长度（B=1），

由于U_C为材料常数，根据dν₁=2πBrdr得到：

将式（13）、（15）、（18）以及（19）代入式（10），化简得到：

式（20）即为强度丧失的临界半径，其大小与表面能和材料弹性模量成正比，与临界能量耗散值U_C 成反比。

3 基于能量耗散原理的临界爆破能

若考虑爆破所产生的能量变化，单位岩体爆破所需能量为 U_b，这部分能量可看作是外界对围岩体系做功，把这部分能量代入巷道岩体强度丧失准则 （10）中可以得到：

式（21）中：${\int }_V{U}_b\mathrm{d}v={\int }_0^{R_0}2\pi B{U}_{b}r\mathrm{d}r$。

按照上述推导过程，得到单位岩体的临界爆破能：

式（22）中，单元能量临界耗散值 U_C、围岩应力 p₀、泊松比ν以及弹模E都可以根据工程实测及实验得到，而且在围岩不变时，其值为常数，因此单位岩体的临界爆破能与巷道的开挖半径密切相关且成反比关系，巷道设计半径越大（在围岩稳定情况下），用于单位岩体的爆破能越小，反之则越大。

基于巷道围岩的稳定性，假设巷道爆破岩体出现裂纹时认为爆破成功。此外，假设单位岩体临界破坏能量为 U_d，其可通过试验测得。因此，当临界爆破能大于岩体的临界破坏能时，围岩体不稳定，爆破能过剩；当临界爆破能等于岩体临界破坏能时，围岩体正好临界状态，爆破能最优；当临界爆破能小于岩体临界破坏能时，不能巷道开挖，爆破能不足。因此得到临界爆破能准则：

需要指出的是，在实际工程应用中，将半无限问题的求解应用到围岩应力求解中。假设在巷道开挖之前，原岩未发生任何破坏（即围岩体中不存在裂纹或损伤，有时候甚至出现破坏面），即围岩体是完整的，实际上，围岩体在未开挖之前一般是存在微裂纹或已经发生了一定程度的损伤。计算理论因忽略了这些原因而造成的误差尚不能精确求出解析解，还有待室内试验、现场实测、数值模拟以及工程经验进行验证并进行修正。此外，理论推导过程中只考虑了开挖半径 5R₀范围内的围岩体，在深井巷道开挖过程中比较合理，但是在浅埋巷道开挖过程中，半径 5R₀外的围岩体对巷道内应力场的影响是不能忽略的。因此，公式的适用范围为深埋巷道围岩体开挖。

4 实例分析

4.1 巷道开挖临界半径分析

某深井巷道开挖半径设计中，垂直埋深 h=600 m 左右；原岩初始垂直应力值为 P₀=24 MPa，表面能密度 r=5.19 kJ·m^-2，单元能量临界耗散值 U_C=156 kJ·m^-3，依据式（19）可计算临界半径为：

$\begin{array}{c}{R}_0=\frac{2\times 5.19\times {10}^3\times 31\times {10}^3}{24\times 31\times {10}^3\times 156+(0.54-3.96\times 0.2)\times {24}^2}\\ \approx 2.772\left(m\right)\end{array}$

由上式可见，在深井巷道开挖中，理论上讲，巷道半径 R₀设计为临界值 2.772 m 时，巷道围岩在不经过支护的情况下处于临界稳定，但是，为了安全，可根据具体工程实际设计安全系数。

综上所述，巷道围岩参数对开挖临界半径的取值影响较大，采用变量控制法对上述各因素进行深入研究分析，画出巷道开挖半径临界曲线图。

由图5 可看出，随着巷道围岩的弹性模量的改变，巷道临界开挖半径没有改变，因此，在深埋巷道围岩开采过程中，围岩弹性模量对巷道临界开挖半径几乎没有影响，在巷道开挖半径设计时，可以不考虑围岩弹性模量的影响。

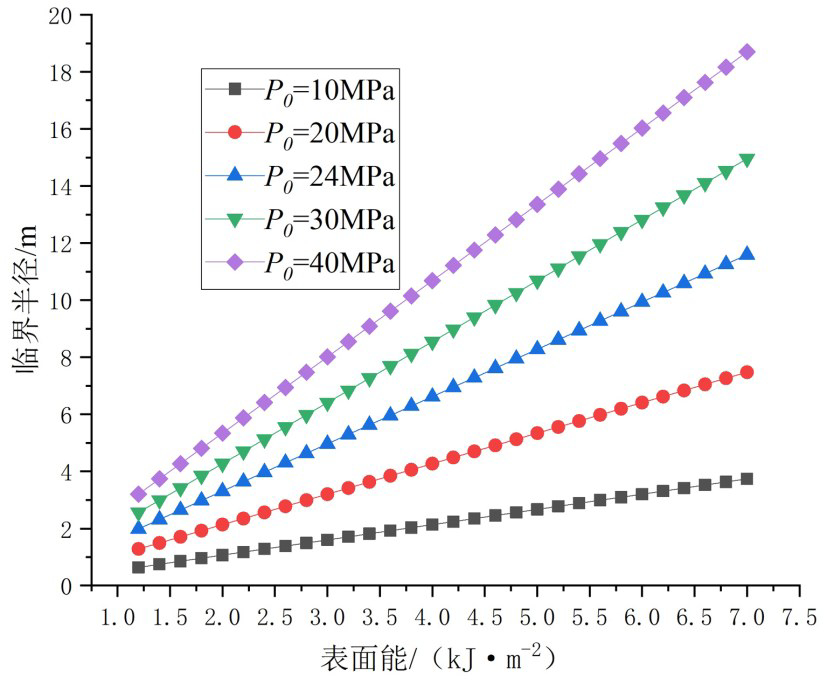
由图6可看出，随着围岩表面能的增大，巷道开挖临界半径也在增大，两者之间近乎呈线性变化，P₀=10 MPa，围岩表面能从1.2 kJ·m^-2 变化到7.0 kJ·m^-2 时（表面能扩大约 5.83 倍），巷道开挖临界半径从 0.641 m 变化到 3.739 m（临界半径扩大约 5.83 倍）。因此，巷道开挖之后形成的围岩面表面能越大，围岩面吸收的能量越多，系统中用于围岩损伤、裂纹开展的能量就越少（因为系统能量符合不可逆的能量守恒定律），围岩也就越稳定，开挖临界半径也就越大。

巷道埋深不同，原岩应力也随之变化（李本召等，2020；吕超等，2022），因此考虑不同围岩应力下的巷道临界半径，画出两者之间的曲线图（图7）。

由图7可看出，在保持其他参数不变的情况下，随着围岩应力增大，临界半径的取值几乎没有改变，因此，理论上来讲，巷道开挖半径设计值与围岩应力值关系不大。

综上所述，巷道临界开挖半径与围岩的表面能关系密切，深入分析巷道临界半径，为方便计算，在满足计算精度的情况下，巷道临界半径式（20）可以简化为：

式（24）即为巷道临界半径工程近似计算公式，在特定围岩条件下，巷道开挖临界半径与表面能成正比。临界开挖半径的准确性与单元体强度丧失时临界能量耗散值的测定精度有关，其实验测得的数据越接近工程实际，则临界半径计算值就越符合要求。

4.2 巷道临界爆破能分析

巷道工程中，常采用爆破法进行开挖。但是爆破能的合理控制已成为巷道安全开挖的重要前提。设有一深埋巷道，其围岩参数如表1，将各参数代入单位岩体的临界爆破能计算公式（21）得到：

$\begin{array}{c}{U}_b=\frac{(3.96\times 0.2-0.54)\times 24\times 24}{31\times {10}^3}\\ +\frac{2\times 5.19}{2.772}-24\times 0.156\approx 0\end{array}$

由上述结果可得，在巷道的临界半径开挖中，是不允许有爆破能的。结合式（22、23），在满足 U_b= U_d时，计算巷道最优开挖半径：

式（25）中，单位岩体临界破坏能量 U_d需经过实验室实测得到。

4.3 重点分析

在巷道开挖中，开挖半径的选取将会对巷道围岩的稳定性产生较大影响，因此，在无支护条件下，巷道开挖半径设计时需要综合考虑已有的工程资料和现场勘探资料，结合实验室测得的围岩基本参数，全面分析巷道开挖半径最优值；同时，考虑爆破能对巷道开挖稳定性的影响，为使爆破能满足开挖要求，其使用药量必须足够，但是，若药量太多，会引起巷道失稳，影响施工安全。所以，结合临界爆破能准则，优化开挖半径，使得爆破能得到充分应用的同时，还可以确保巷道围岩的稳定性。

5 结论

（1）深入研究巷道开挖过程中的能量耗散与释放，基于能量原理及围岩应力场分布，提出巷道围岩能量耗散与释放的计算模型。类比损伤力学中的损伤因子，给出了能量损伤因子的物理定义和表达式。

（2）在能量耗散与释放计算模型的基础上，基于能量守恒定律，推导出巷道围岩强度丧失的临界开挖半径以及临界爆破能；基于临界爆破能与单元围岩体的临界破坏能，提出了临界爆破能准则。

（3）通过工程实例分析，得到巷道临界开挖半径受到围岩表面能的影响较大，而受围岩弹性模量与原岩应力的影响较小。同时，在全面分析各参数与巷道临界开挖半径之间计算关系的基础上，对巷道开挖临界半径进行了简化计算，得到工程应用中的巷道临界开挖半径计算关系。基于临界爆破能准则，得到巷道最优开挖半径解析解。

参考文献