摘要
针对成矿预测领域中负样本开采难度大、工作量大，导致成矿预测效果不理想的问题，本文将机器学习技术引入成矿预测研究中，构建了基于PU算法的多金属矿成矿预测模型。首先对模型整体框架进行设计，然后构建数据集对模型进行训练与测试。测试结果表明：基于PU的成矿预测模型收敛速度快，损失值仅为0. 08，在测试集上的平均准确率为92. 5%，AUC值为0. 96，成功预测34个矿点，且不存在非矿点样本，最接近实际矿点数量，仅有1个矿点未成功识别。与基于PCA、RF、SVM的成矿预测模型相比，整体性能良好，识别能力强、分类效果最佳，预测结果最可靠，在样本数据欠缺的情况下，可以获得良好的成矿预测效果。
Abstract
In response to the difficulty and heavy workload of negative sample mining in the field of mineralization prediction，which leads to unsatisfactory mineralization prediction results，this paper introduces machine learning technology into mineralization prediction research and constructs a multi metal mineralization prediction model based on the PU algorithm. Firstly，design the overall framework of the model， and then construct a dataset to train and test the model. The test results show that the PU based mineralization prediction model has a fast convergence speed， a loss value of only 0. 08， an average accuracy of 92. 5% on the test set， and an AUC value of 0. 96. It successfully predicted 34 ore points without any non ore point samples， which is closest to the actual number of ore points. Only one ore point was not successfully identified. Compared with mineralization prediction models based on PCA， RF， and SVM， the overall performance is good， with strong recognition ability， the best classification effect， and the most reliable prediction results. In the case of insufficient sample data， good mineralization prediction results can be achieved.
Keywords
0 引言
随着全球经济的快速发展，各国对矿产资源的需求越来越大，导致目前已知的矿产资源储量日益紧缺，因此寻找新的矿源成为目前资源开发领域中最紧迫的工作之一。其中，金属矿对工业发展的影响重大，对其进行寻找和预测对全球经济发展具有重要作用。20世纪20年代以来，不断有研究者提出成矿预测方法。国外率先将机器学习引入到找矿工作中，如神经网络（Puzyreva et al.，2023）、支持向量机（Zhang et al.，2022）、随机森林（Xiao et al.， 2021）等，利用大数据处理能力和自适应能力进行成矿寻找与发掘（Davies et al.，2020；Li，2021），取得了较好的应用效果（Black，2019）。国内学者重点利用机器学习的识别与预测功能（秦耀祖等，2021），对地球化学勘探数据进行充分挖掘（郭广慧等， 2023），采用对数比方法进行数据处理，获取成矿预测要素（石娴等，2023；吴巍辉和吴雄辉，2023），然后通过机器学习的方式进行找矿信息集成，在成矿预测领域取得了较为显著的进展（李瀚波等，2022； 欧阳渊等，2023）。韩世礼等（2024）论证了机器学习技术应用于成矿预测领域，可以让地球物理勘探取得更加全面、精准和高效的成果，其在铀矿资源勘察工作中取得了显著的效果。呼冬强等（2024） 采用随机森林算法对新疆木吉一带金矿区域进行成矿预测工作，验证其拥有巨大的金矿找矿潜力。刘嘉情等（2023）借助机器学习算法，建立可以识别成矿岩体和贫矿岩体的新方法，极大提高了找矿效率。综上可知，机器学习技术在找矿和成矿预测领域应用效果较好，具有一定的优势（Lavlinskii et al.， 2022；李希元等，2022；Zhang et al.，2022；王昊等， 2023）。但受制于目前负样本数量十分欠缺的现状，导致最终预测结果不够理想、勘探成本高（韩创益等，2017； Li，2021；李猛猛等，2022）。本文的创新点在于针对这一问题，选择 PU 半监督学习算法构建多金属矿成矿预测模型，该算法可以在样本数量十分欠缺的情况下，仅利用少量的正样本进行机器学习，即利用少量的已标记矿点数据对预测模型进行训练和测试，并取得较好的预测效果，减少了负样本（未标记的矿点数据）开采的工作量，同时提高了负样本选取的正确性和科学性，与成矿预测模型十分相合，对进一步推动成矿预测工作的开展，降低成矿勘探的人力、物力成本，具有一定的研究意义。
1 成矿预测模型
1.1 模型整体框架设计
目前，常用数据分析包括机器学习方法、多重分形方法、T 统计量分析方法等（Liu and Jing， 2012）。其中，机器学习在成矿预测领域具有较好的应用效果。根据数据是否存在标签，可以将机器学习分为有监督、无监督和半监督 3 种学习模式。考虑到已经标记好的矿点数据较少，而矿点负样本需要大量的人力、物力以及时间去开采，导致常用的机器学习算法受现有数据限制，存在收敛速度慢、泛化能力低、成矿预测效果不够理想等问题。因此，本文以海相火山沉积型铁矿为研究对象，采用正无标记学习（Positive Unlabeled Learning，简称 PU）算法作为机器学习方法对矿点数据进行分析处理，构建多金属矿成矿预测模型。本文设计成矿预测模型的整体框架如图1所示。
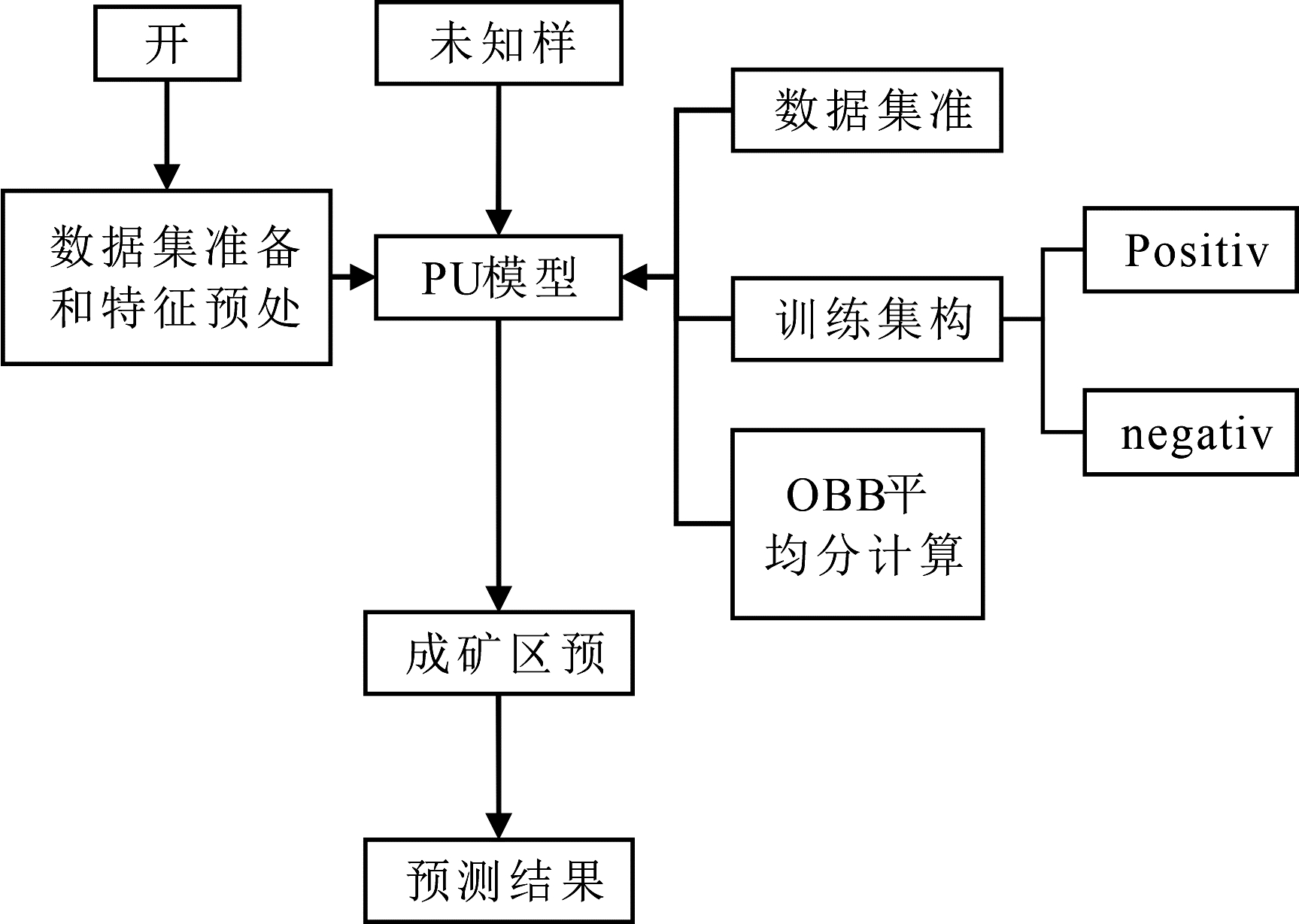
图1多金属矿成矿预测模型
由图1可知，本文设计的多金属矿成矿预测模型主要包括数据集准备和特征预处理、PU 模型训练、成矿区预测3个模块。其中，数据集准备和特征预处理的主要任务是对找矿信息进行提取，然后输入至训练完成后的 PU 学习模型实现找矿信息的集成。成矿区预测模块根据找矿信息对未知样本进行分析，实现成矿区预测并输出预测结果。
1.2 模型原始输入特征
本文选择东天山地区（88°30’～96°30’E，41° 30’～42°30’N）作为研究区，该地区位于中国境内天山造山带东部，整体呈低山丘陵-平原地貌。研究区出露地层主要为石炭纪火山沉积岩，岩浆岩分布广泛，典型特征为发育雅满苏组双峰式火山岩和沉积岩夹层。研究区主要控矿构造为次生断裂，主要生成海相火山沉积型铁矿，赋矿地层为雅满苏组，典型矿床为雅满苏铁矿。则成矿预测模型的原始输入特征包括构造、岩体、地层以及地球化学元素。
2 数据分析方法和数据准备
2.1 正无标记学习算法
PU 算法是半监督学习的一种特殊的机器学习范式，常用于处理分类问题。其基本原理是通过将训练数据分为有标记的正样本和没有标记的未标记样本来处理分类问题，分类方式包括单分类算法和两步法。
单分类方式的实现步骤为：（1）随机从数据集中选择部分样本进行标记；（2）构建训练集。随机抽取数量相同正样本与未标记样本，并分别记为 Positive、negative；（3）构建分类器。通过bootstrap抽样方法进行多次重复抽样为分类器构建提供充足样本；（4）计算袋外样本（Out of Bag，简称OBB）。将数据集余下的未标记数据输入分类器，并根据输出结果获得概率分数，即 OBB；（5）重复步骤（1）～（4），获得新的 OBB；（6）对数据集中余下所有未标记样本的OBB进行计算并获得综合平均分，输出最终结果。
两步法的基本原理为不断重复负样本选取和训练两个步骤，获得最终的既定标准来处理分类问题。第一步，选取可靠性良好的负样本。选取方法为通过标准分类器计算正样本的分数范围，在此范围内进行负样本选取。第二步，负样本训练。训练方法为构建第二个分类器，从第一步选取的负样本上进行训练。
考虑到矿产资源预测需要针对大量的无标签数据进行信息特征挖掘，因此本文采用 PU 算法中的单分类算法对找矿信息进行探查，挖掘矿点特征数据。
2.2 数据准备
2.2.1 基础数据
本研究采用的基础数据为 1∶20 万水系沉积物地球化学数据，该数据包含了39种地球化学元素和氧化物含量，如Ag、As、Au、B等；1∶20万数字化区域地质图数据，该数据包含了若干地质体空间信息，如构造、侵入岩、岩体、沉积建造等；区内铁矿点位置分布图数据，该数据包含了本文研究区内所有已知的铁矿点位置。以上述 3 种数据为基础，在 GIS 平台上对控矿信息进行提取和处理。
2.2.2 构造特征数据提取
根据研究区的构造特点，首先根据前人文献资料提供的经验，为样本添加构造形迹特征和构造交汇点特征。构造形迹特征构建思路：（1）在 GIS 中，采用多环缓冲区工具构建一个10环缓冲区，环与环之间的间隔设置为 1 km；（2）统计样本点（矿点）落入不同环内的数量以及位置；（3）根据统计结果构建构造形迹特征；（4）采用赋值法对缓冲区内样本点的断裂特征进行赋值，0～1 km 赋值为 10，1～2 km 赋值为 9，2～3 km 赋值为 8，以此类推，9～10 km赋值为1，缓冲区外赋值为0。
构造交汇点特征构建思路同上。
2.2.3 地层及控矿岩体特征数据提取
根据研究区内地层特点和矿床形成原理，本文对地层及控矿岩体特征构建思路如下：（1）在 GIS 中，采用多环缓冲区工具构建一个以酸性侵入岩与围岩接触线为中心点，生成以接触线→围岩为方向的缓冲区；（2）统计落入缓冲区内的样本点范围，为其添加岩体控矿属性；（3）在GIS软件中的多环缓冲区工具，设置中酸性侵入岩体与围岩的接触带为中心点，生成间隔为 0.5 km 的缓冲区，并对落入缓冲区内的样本点进行赋值，获得岩体控矿特征值，为样本点添加地层及控矿岩体特征。
2.2.4 地球化学特征提取
本文构建成矿预测模型的基础数据之一为 1∶20万水系沉积物地球化学数据，该数据在录入和传输过程中受到其自身形式的限制会产生许多误差，若直接使用会导致成矿预测模型的最终预测精准度效果不理想，因此需要对收集到的研究区内水系沉积物地球化学特征数据进行预处理。
（1）采用中位数法进行去极值操作，在保证样本数量不变的情况下，去除数据中与常规数值分布存在明显偏移的数据，降低其对统计量的影响。
（2）采用离差标准化方式对原始数据进行线性变换，变换公式可以表示为：
(1)
式（1）中，x代表线性变换前的地球化学元素含量；x*代表变换后的元素含量；min代表元素含量最低值；max代表元素含量最高值。
经过式（1）的线性变化，可以将地球化学元素含量缩放到 0～1 之间，继而消除数据量纲差异，同时最大程度保留原始数据的分布特征和连续性。
（3）采用距离反比插值法对离散的采样点进行插值，其计算公式可以表示为：
(2)
式（2）中，t（xi）代表第 i个采样点的地球化学元素浓度值；t代表等待被加权采样点的地球化学元素浓度值；n 代表用于元素插值的采样点数量；p 代表距离幂次方；di代表等待插值采样点到第i个普通采样点之间的距离。
距离反比插值法的主要作用是保证研究区内地球化学数据的连续性。
2.2.5 训练样本构建
训练样本构建是成矿预测模型拥有良好综合性能与预测精准度的关键。根据前人对矿点正负样本的选择经验，本文首先选择研究区内35处已知矿点作为正样本；然后根据海相火山沉积型铁矿的地层特征，将存在与成矿相关地层或岩体的区域进行排除；之后，采用多距离聚类分析方法获取矿点聚类范围；最后在矿点聚类范围之外，已经排除存在与成矿相关地层或岩体区域的研究区内，随机生成35处无矿点作为负样本。
2.2.6 数据集划分
考虑到本文样本数据较少，故而本文数据集划分方法采用针对少量数据划分效果良好的K折交叉验证方法。具体划分步骤为：（1）本文数据集中共包含共70个样本，将其随机等分为K份，K值设定为 7；（2）从7份数据中随机选择一份作为测试集，剩余 6 份作为训练集；（3）根据上一步骤的划分结果，训练集用于模型训练，其后采用训练完成的模型对测试集进行测试，并计算准确率；（4）排除已经作为测试集的1份样本，从剩余6份样本中重新随机抽取1 份作为测试集，余下 5 份样本同上一步骤中作为测试集的样本一起作为下一步骤的训练集；（5）根据上一步骤的划分结果，再次对模型进行训练，并计算其在测试集上的准确率；（6）采用步骤（4）同样的思路，重新划分训练集与测试集对模型进行训练，直到7份样本都分别作为测试集进行模型训练与测试，一共进行 7 次，计算 7 次测试的平均准确率，将其作为成矿预测模型的最终准确率。
上述数据集划分方法可以有效消除少量数据划分对模型预测精度造成的偏差影响。
3 结果与分析
3.1 PU算法验证
3.1.1 实验环境和参数设置
实验环境：MATLAB仿真平台，内核处理器-i7-9700KF，PLC 编程软件，训练框架-Tensorflow，编程语言-Python。
参数设置：PU 算法采用单分类算法，循环次数设置为 1000 次，每次训练抽取 15 个矿点数据作为正样本标记，训练器采用决策树，相关参数选择默认值。
实验对照组参数设置：训练迭代次数500次，学习率0. 001。
3.1.2 评价指标
本文采用准确率（Accuracy，简称 ACC）和 ROC 曲线的曲线下面积（Area under the curve，AUC）作为成矿预测模型的评价指标。其中，ACC的计算公式可以表示为：
(3)
式（3）中，TP、TN 分别代表模型预测为正的正样本数量和负样本数量；FP、FN分别代表模型预测为负的正样本数量和负样本数量。
ROC曲线以伪阳性率为横坐标，真阳性率为纵坐标，根据每一个分类阈值可以得到对应的伪阳性率值和真阳性率值，即一个坐标点，通过不断调整和改变阈值，将计算获得的坐标点进行连接，获得 ROC 曲线。而 ROC 曲线与坐标轴之间形成的阴影部分面积大小被称为AUC值，其取值范围是[0，1]， AUC值越接近1，代表模型预测结果越可靠，反之预测效果差。 ROC 曲线和 AUC 值的关系如图2所示。
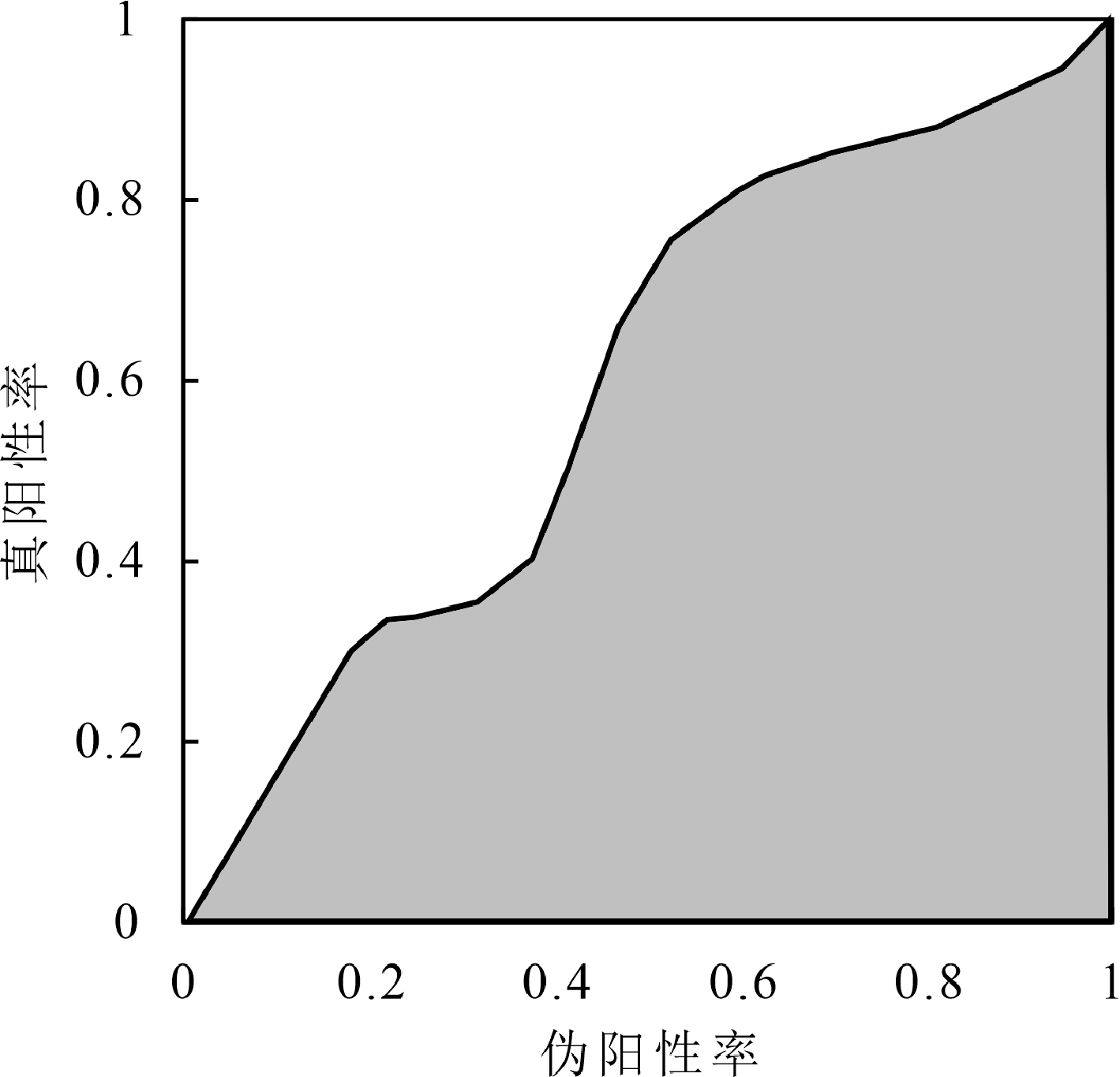
图2ROC曲线和AUC值
3.1.3 算法验证结果与分析
本节采用第2节收集的数据和数据集划分方法对 PU 算法模型进行训练与测试，同时以支持向量机（Support Vector Machine，简称 SVM）和随机森林 （Random forest，简称 RF）两种监督学习算法模型，以及主成分分析（Principal Component Analysis，简称 PCA）的无监督学习算法模型作为实验对照组，验证 PU算法的优越性。
不同算法模型在训练时损失值与迭代次数的变化曲线如图3所示。
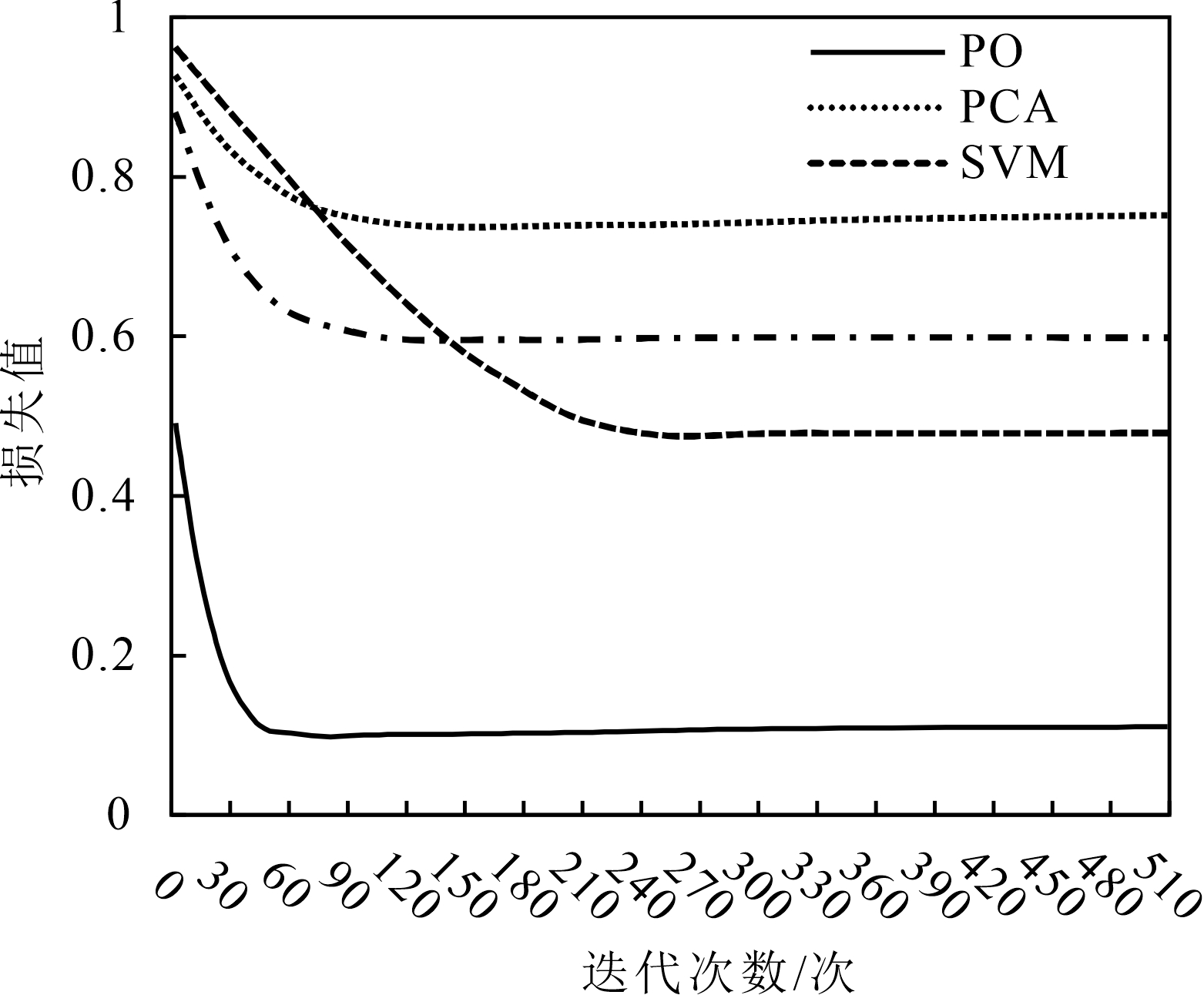
图3不同算法模型训练结果
分析图3可知，PCA 无监督学习算法构建的分类模型在经过 170 次迭代后开始收敛并趋于平稳，损失值维持在0.75左右，综合性能最差。SVM算法模型在经过 260 次迭代后开始收敛，损失值维持在 0.42 左右，RF 算法模型在经过 80 次迭代后便开始收敛，损失值维持在0.6左右，表明两种监督学习算法模型的综合性能都比PCA好，但SVM算法收敛速度慢，RF 算法损失值高，在成矿预测领域的表现效果不够理想。本文选择的PU算法模型在经过50次迭代后便开始收敛并趋于平稳，损失值维持在0. 08 左右，收敛速度快，损失值极低，表明其在成矿预测领域具有显著的优势。本文选择 PU 算法构建成矿预测模型具有合理性和有效性。
对不同算法模型进行测试并计算各自的平均准确率。测试结果如图4所示。
图4平均准确率对比
分析图4可知，PCA 无监督学习算法在测试集上的准确率仅为 59.1%，明显不适用于成矿预测。 SVM 有监督学习算法和 RF有监督学习算法在测试集上的准确率分别为78.2%、71.4%，在成矿预测领域具有较好的应用效果，但仍旧不够理想。本文选择的 PU 半监督学习算法在测试集上的准确率达到了 92.5%，明显比其他学习算法的准确率高，表明 PU半监督学习算法在矿点数据样本极小的情况下，可以构建十分理想的成矿预测模型，验证了其自身的优越性和本文选择的合理性。
对不同算法模型进行测试并绘制ROC曲线，并计算各自的AUC值。测试结果如图5和表1所示。
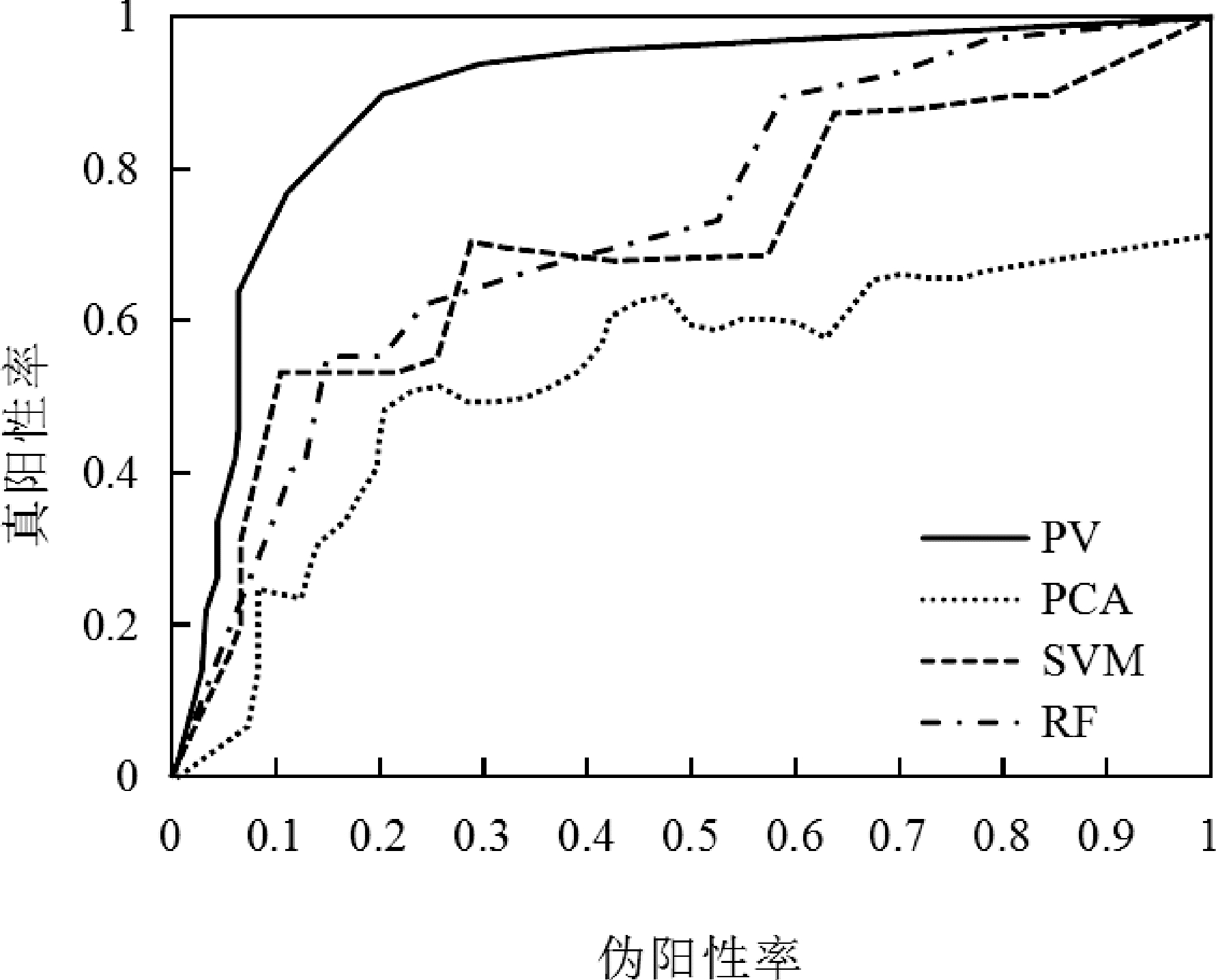
图5不同算法模型的ROC曲线图
表1不同算法模型的AUC值计算结果
分析图4和表1可知，PCA 无监督学习算法构建的预测模型 AUC 值仅为 0.52，预测效果最差。 SVM 和 RF 两种有监督学习算法构建的预测模型 AUC值分别为0.80和0.77，预测效果稍好。本文选择的PU半监督学习算法构建的预测模型AUC值达到了0.96，无限逼近于1，表明该模型的预测结果最可靠。
3.2 成矿预测结果与分析
本小节在仿真平台上对基于机器学习的多金属矿成矿预测模型进行测试，并对其成矿预测结果进行分析。测试方法：在仿真平台上导入研究区轮廓图，根据已知矿点进行区域划分，即成矿高概率区标为红色，记为一级成矿远景区，成矿中概率区标为橙色，记为二级成矿远景区，成矿低概率区标为绿色记为三级成矿远景区。采用同2.2.5小节相同的方法建立数据集，包括 35 个已知矿点和 35 个已知非矿点，共计70个数据样本。利用不同算法构成的成矿预测模型对数据集中样本进行预测，预测为“成矿矿点”则落入研究区内的成矿远景区中。最后统计数据集中矿点和非矿点落入不同成矿概率区的数量。
图6统计了不同成矿预测模型落入成矿远景区内的“矿点”和成矿远景区外的“非矿点”。分析图5可知，PCA仅成功预测了18个矿点样本，RF和SVM 预测模型分别成功预测了22、21个矿点样本，PU预测模型成功预测34个矿点样本，最接近实际矿点数量，仅有1个矿点未成功识别，预测结果最可靠。
分析表2可知，PCA 模型预测的矿点中，有 6个属于非矿点样本，表明模型无法很好地分辨出矿点与非矿点，无法准确地对数据样本进行分类，预测效果差。RF 模型预测的矿点中，有 4 个非矿点样本，SVM 模型预测的矿点中，有 2 个非矿点样本，表明这两个模型在预测时，对矿点与非矿点的分类效果较强。本文选择的 PU 名模型预测的矿点中，不存在非矿点样本，34 个预测矿点与实际矿点相符，分类效果最佳。
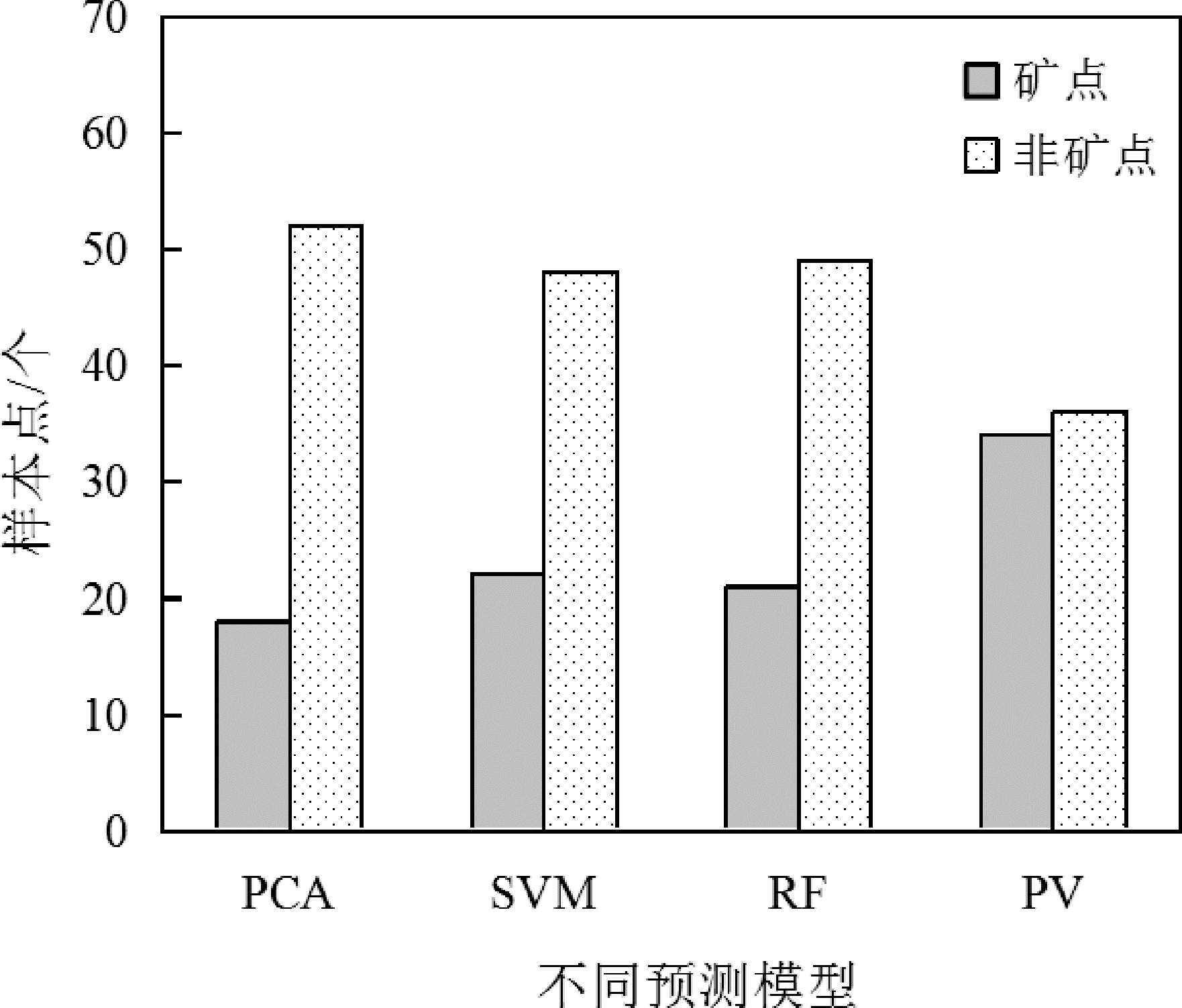
图6不同模型的成矿预测结果
综上，基于 PCA 的成矿预测模型收敛速度慢，整体性能差，在测试集上的平均准确率仅为 59.1%，AUC 值仅 0.52，预测效果差，对成矿进行预测时仅识别出 18 个矿点样本，且其中仅有 12 个正确的矿点样本，识别能力和分类效果都极差。基于 RF 的成矿预测模型收敛速度较快，但损失值高，在测试集上的平均准确率为 78.2%，AUC 值为 0.77，成功预测的 22个矿点中存在 4个非矿点样本，模型整体性能较好，但矿点识别能力和分类效果不够理想。基于SVM的成矿预测模型损失值低，但收敛速度慢，在测试集上的平均准确率为 71.4%，AUC 值为0.80，成功预测的21个矿点中存在2个非矿点样本，模型整体性能、矿点识别能力以及分类效果和基于RF的成矿预测模型相差不大。基于PU的成矿预测模型收敛速度快，损失值仅为 0. 08，在测试集上的平均准确率为 92.5%，AUC 值为 0.96，成功预测 34 个矿点，且不存在非矿点样本，最接近实际矿点数量，仅有1个矿点未成功识别，其模型整体性能良好，识别能力强、分类效果最佳，预测结果最可靠，十分适用于数据样本数量极少的成矿预测工作。
表2不同模型预测的“成矿矿点”中包含正确矿点和非矿点的统计结果
4 结语
本文提出了一种基于机器学习的多金属矿成矿预测模型。针对成矿预测领域已知矿点样本数据较少的问题，选择 PU 半监督学习算法对模型进行构建，利用极少的数据完成模型训练和测试。测试结果表明，相比于目前在成矿预测领域常用的分类算法，基于 PU的成矿预测模型收敛速度快，损失值为 0. 08，预测平均准确率为 92.5%，AUC 值为 0.96，预测效果可靠，更适用于数据样本极少的成矿预测工作，具有一定研究意义。但受实验时间限制，本次研究负样本可供选择的数量较少，同时特征信息提取不够全面，都可能对最后的预测结果造成影响，后续要扩充负样本数量，进一步提取成矿信息，对模型进行完善，为多金属矿成矿预测研究提供参考。
图(6)
/
表(2)
手机扫码阅读
引用本文
孙富海. 2024. 基于机器学习的多金属矿成矿预测和评价［J］. 矿产勘查，15（s2）：78-84.
复制
Sun Fuhai. 2024. Machine learning based prediction and evaluation of polymetallic mineralization［J］. Mineral Exploration，15（s2）：78-84.
Copy
计量
文章访问量:
HTML全文浏览量:
PDF下载量: